阶段模型修正的星载GNSS-R土壤湿度反演方法
陶庭叶,李江洋,朱勇超,2,汪俊涛,陈 皓,时梦杰
1. 合肥工业大学土木与水利工程学院,安徽 合肥 230009; 2. 土木工程防灾减灾安徽省工程技术研究中心, 安徽 合肥 230009
土壤湿度调节着陆地、大气和其他水文过程之间的能量和水分交换,在全球范围内的水文和地球物理过程中发挥着重要作用,是全球气候变化研究的关键参数[1-3]。因此,获取高时间和空间分辨率的土壤湿度是十分重要的。土壤湿度探测方法经过多年的发展,内容已经非常丰富。传统的人工实地测量方法精度较高,但这种方法费时费力,无法满足现代大规模获取土壤湿度数据的需求[4]。微波遥感技术利用微波频率信号对土壤介电常数的敏感性获取全球尺度的土壤湿度数据。目前,用于土壤湿度探测的卫星包括SMAP[5](Soil Moisture Active Passive)和SMOS[6](Soil Moisture and Ocean Salinity),但微波遥感卫星造价较高,且单颗卫星重访时间较长,限制了其应用。
近年来,利用星载GNSS-R(global navigation satellite system reflectometry)[7]探测土壤湿度成为研究热点。GNSS-R通过接收地球表面反射的GNSS卫星信号来反演反射面特性[8],具有以下特点:①GNSS卫星L波段信号对土壤含水量有着较高的敏感性,且对云雨雾具有良好的穿透性,受气象条件影响较小;②GNSS-R接收机体积小、重量轻、功耗低,因此,搭载GNSS-R接收机的小卫星制造成本较低,可以利用较低的成本生产若干颗GNSS-R小卫星组成一个星座,提高时间分辨率;③使用现有GNSS卫星免费的信号源,信号覆盖范围广[9]。总之,GNSS-R土壤湿度反演具有低成本、无源探测、全球覆盖、高分辨率、获取数据量大等优势,且具备全天候、全天时工作能力[10]。文献[11]使用英国航天局的TDS-1(TechDemoSat-1)数据进行全球土壤湿度反演。由于TDS-1的数据采集在空间和时间覆盖方面受限严重,无法实现土壤湿度的每日估计。NASA于2016年发射的CYGNSS(cyclone global navigation satellite system)卫星星座,由8颗微小卫星组成,提供的数据量比TDS-1多几个数量级,较好地解决了GNSS-R反演土壤湿度的时空覆盖问题。文献[12]基于CYGNSS数据的GNSS-R土壤湿度反演,发现天鹅座信噪比(SNR)的变化与SMAP土壤湿度结果相关,并通过线性回归方法解释了相关性。文献[13]利用相对信噪比与SMAP提供的土壤湿度数据相结合获取每日土壤湿度估计值。文献[14]提出反射-植被-粗糙度(R-V-R)算法,推导每日土壤湿度估计值。文献[15]分析时间序列并进行土壤湿度反演,通过SMAP土壤湿度值的最大值和最小值来限制其土壤湿度反演结果。文献[16]提出基于3层模式的泛热带土壤湿度反演方法。
值得注意的是,上述土壤湿度反演模型都是为了减弱植被和地形对反演结果的影响,而在实际应用中,温度也影响着土壤湿度的变化。文献[17]研究了海面温度与CYGNSS数据中时延多普勒图的关系,其中时延多普勒图是反射面的散射功率与传输的GNSS信号模糊函数进行卷积的结果,而反演土壤湿度使用的反射率需要基于时延多普勒图计算,因而对全球范围土壤湿度进行跨季度反演,温度因素是不可忽略的。此外,上述模型还存在大量输入辅助数据的问题,使得模型训练过于复杂且耗时,同时对土壤湿度较高的区域反演存在较大误差。
本文提出阶段模型修正的星载GNSS-R土壤湿度反演方法。首先,通过处理CYGNSS数据获取地表反射率参数,以SMAP提供的植被、地面及温度信息作为辅助数据,使用神经网络线性回归模型来进行数据训练,构建土壤湿度反演初始模型;然后,利用阶段模型进行更高精度土壤湿度的反演。相比较先前的研究,本文方法使得反演的土壤湿度更贴近现实情况,且提高了时间和空间分辨率。
1 理论和方法
本节介绍了星载GNSS-R反演土壤湿度的基本原理和具体的反演流程。
1.1 基本原理
GPS卫星、地面和接收器构成双基地雷达系统,接收GPS卫星发送的L波段电磁波信号获得与散射表面特性相关的信息。土壤湿度作为陆地信息的一部分能够被反演,因为它是散射表面介电常数的主要决定因素。一种理想的基于GNSS-R的土壤湿度反演方法是依靠双基地雷达方程的反演来获得地表反射率。地表反射率通过对植被覆盖和表面粗糙度的影响进行校正,以获得菲涅尔反射系数。利用菲涅耳反射方程,建立菲涅耳反射系数与土壤湿度之间的数学模型。
对于镜面反射占完全主导地位的情况,双基地接收功率的相干分量如式(1)所示[18]
(1)

假设地面相对平坦(无地形起伏)和光滑(弱粗糙度),没有或少量植被覆盖时,双基地接收信号由相干反射控制,此时表面反射率可直接计算,如式(2)所示
(2)
通过使用式(2)计算地面反射率后,应从Γrl(θ)提取菲涅尔反射系数Rrl(θ)。因为菲涅尔反射系数主要受土壤含水量影响。假设植被下的表面是平坦光滑的,Rrl(θ)可以通过校正Γrl(θ)的植被和表面粗糙度效应计算获取,如式(3)所示
Γrl(θ)=Rrl(θ)2γ2exp(-hcos2θ)
(3)
式中,γ2是波从植被冠层顶部传播到地面,然后再从地面传播到植被冠层顶部时的波衰减;h参数与表面粗糙度均方根高度线性相关。
借助菲涅尔方程将菲涅尔反射系数与土壤介电常数关联,如式(4)—式(6)所示
(4)
(5)
(6)
式中,Rvv和Rhh为水平和垂直偏振下的菲涅尔系数;θ为入射角;εr为表面介电常数,εr=ε/ε0-j60λσ,其中,ε0为自由空间介电常数,σ为电导率,λ为波长,在干燥地形或几乎干燥的情况下,介电常数的虚部可以忽略。利用土壤质地信息,借助于地面介电混合模型,可以通过土壤介电常数εr获取土壤湿度[19]。
1.2 反演方法
本文基于CYGNSS数据利用GNSS-R进行土壤湿度的反演,首先需要对CYGNSS数据进行预处理,通过每个镜面点处的信噪比来进行数据筛选,将信噪比小于0及入射角大于60°的数据剔除以保证数据质量。基于预处理后的数据提取所需要的相关参数,进而计算地表反射率。根据先前的研究,假定陆地上的反射信号主要由来自地面的相干反射决定[20-22],用于反演土壤湿度的地表反射率,其计算如式(2)所示。
反演土壤湿度所需要的辅助数据及验证数据是通过提取SMAP数据获取的,SMAP数据以EASE栅格格式发布和分发,空间分辨率为36 km,它包含升轨和降轨数据。本文获取升轨和降轨的平均值作为每日数据,然后以3 d为一个周期提取全球覆盖数据。为了便于反演结果与SMAP提供的土壤湿度参考值对比,利用CYGNSS提供的镜面点经纬度数据,将其与SMAP地面点经纬度之差小于0.001°的数据取平均覆盖至SMAP网格中,实现将计算得到的地表反射率按照SMAP网格数据网格化,最终使反演值与参考值相对应。
最后将处理获得的地表反射率进行土壤湿度反演,这需要考虑地表植被及地形等因素的影响[23-26]。本文采用了与文献[14]中R-V-R算法类似的模型,通过神经网络线性回归模型进行数据训练。模型通过利用CYGNSS数据处理获得的地表反射率,以及从SMAP中获取的植被光学厚度、地面粗糙度和温度信息,来实现对土壤湿度的反演。该模型通过将植被光学厚度、地面粗糙度和温度加入反演方程等效于消除这些因素对地表反射率的影响,反演土壤湿度SMCYGNSS的模型如下所示
SMCYGNSS=a·Γmean+b·τ+c·σ+d·t+e
(7)
式中,Γmean是通过对地表反射率以3 d为周期取平均,然后将其进行归一化所得;τ、σ和t分别是从SMAP中获取的植被光学厚度、地面粗糙度及地面温度信息。模型对地面温度t也进行了归一化处理。模型中的回归系数通过神经网络中的线性回归模型训练获取。
本文神经网络回归模型分为3个部分,特征缩放、计算损失和梯度下降。具体流程如下:首先加载数据,包括4个输入特征,即地面反射率、植被光学厚度、地面粗糙度和温度,一个输出特征,即土壤湿度;然后对输入特征进行特征缩放,本文采用了最小-最大值缩放方法。设置各参数初始权重为0,迭代次数为10 000次,学习率为0.01,利用梯度下降法进行权值更新,其原理是损失函数对每个参数求导,利用负梯度对参数更新,完成设定迭代次数后得到线性模型各参数的系数解[27]。
然而,训练反馈的相关系数显示土壤湿度在小于0.35时具有良好的相关性,而在大于0.35时相关性很差。为了解决这一问题,本文尝试对大于0.35的土壤湿度反演值进行后处理,通过使用对数、指数等非线性函数处理土壤湿度反演值,发现对于土壤湿度较大的区域,线性模型得到的土壤湿度值在开方处理后与参考值具有良好的相关性,于是提出利用阶段函数模型来处理线性模型获得的土壤湿度,具体模型如下所示
(8)
式中,SM是利用线性模型所获得的土壤湿度;C是常数项,其值是根据线性模型反演得到的土壤湿度值与参考土壤湿度之差来确定的,通过不断试验,得出取值为-0.2时整体效果最佳。
本文以2018年7月和8月的全球数据作为训练数据,通过神经网络线性回归模型处理获得回归系数,然后利用剩下的数据根据线性模型计算土壤湿度,对计算得到的土壤湿度结果使用阶段函数模型处理,实现对不同程度土壤湿度更精确的反演,总体流程如图1所示。
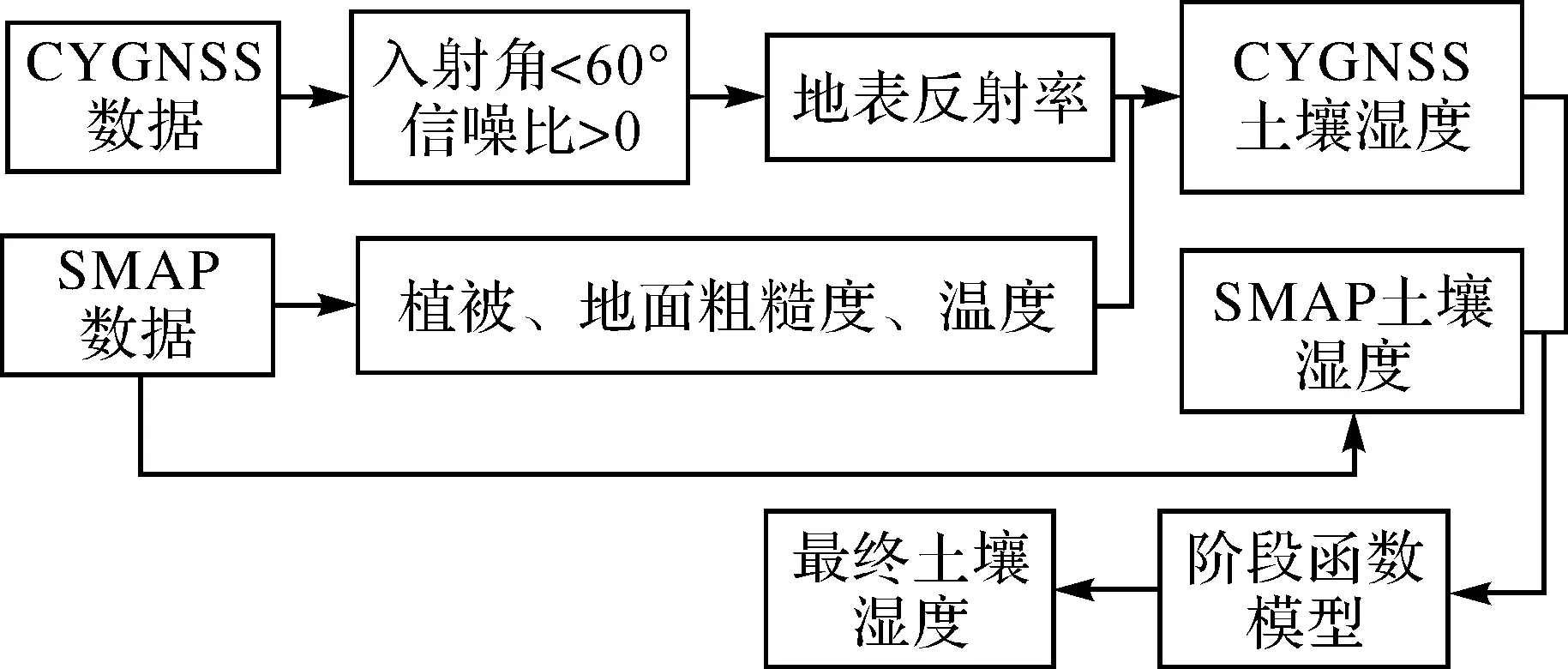
图1 土壤湿度反演 Fig.1 Soil moisture retrieval
2 数据和结果分析
2.1 CYGNSS数据
CYGNSS是由NASA于2016年发射的由8颗微小卫星组成的卫星星座,位于相对赤道倾角35°的低地球轨道上,高度约为500 km。CYGNSS的最初目标是为了观测热带气旋,因此覆盖范围仅限于中低纬度区域(37°S—37°N),但其平均重访时间约为7.2 h,重访时间中位数为2.8 h[28],且数据量极为丰富,因而能够实现大范围和高时间分辨率的土壤湿度探测[29]。
CYGNSS数据可在海洋物理分布式活动档案中心获取,NASA使用netCDF的文件格式封装CYGNSS数据,并将其划分为4个层级(L0~L3),其中L0层由CYGNSS卫星上时延-多普勒测绘仪(delay Doppler mapping instrument,DDMI)的输出数据和未处理的GNSS-R测量数据组成[30]。本文使用的数据是L1级数据,由L0时延-多普勒计数图转化的功率表达结果,主要包括每个镜面点模拟散射功率的延迟多普勒图,以及与镜面点有关的几何信息和导航信息,如入射角、镜面点坐标、镜面点到发射器和接收机的距离等。
2.2 SMAP数据
SMAP是NASA的首颗土壤水分探测卫星,也是继欧空局SMOS之后全球第二颗专注于土壤水分观测的卫星计划。SMAP任务总计已生成24个可分发的数据产品,分别代表4个数据处理级别。1级产品是原始观测数据,并以基于SMAP卫星半轨道的形式出现,半轨道边界根据最北端和最南端的轨道位置划定。2级产品包含基于仪器数据的地球物理反演结果,并且也显示在半轨道中。3级产品是整个UTC(universal time coordinated)一天中2级地球物理检索的每日全球综合信息。4级产品包含使用SMAP数据的地球物理模型的输出。
本文使用的SMAP数据是3级辐射计全球每日等面积可扩展网格数据,该数据可以通过美国国家冰雪数据中心下载[31]。数据空间分辨率为36×36 km2,包含土壤湿度、质量标志和其他辅助信息等[32]。其中,土壤湿度精度为在植被水含量≤5 kg/m2时,地表5 cm内土壤水分探测精度为±0.04,分为升轨和降轨数据。本文使用升轨和降轨的平均值数据作为辅助数据,每3 d为一个周期获取全球覆盖数据。
2.3 模型训练分析
通过将7月和8月的CYGNSS数据与SMAP数据等网格化后,生成200 000个样本数据,在进行噪声数据剔除后,随机分为训练数据和测试数据,分别占95%和5%,通过训练数据获取模型中的系数解,利用测试数据检测获取系数解的效果。这里选取测试数据中的一部分展示预测效果,如图2所示。经计算测试值与估计值的偏差分布,得到整体偏差均值为0.017 8,可以看出,测试数据中的土壤湿度与预测数据较为贴合,整体趋势一致。

图2 测试训练效果Fig.2 Test training renderings
为了进一步验证训练效果,利用后续月份的数据进行土壤湿度反演效果的检验,这里选取了10月份整月的数据为例展示。图3显示了利用训练获得的系数解反演所得到的CYGNSS土壤湿度与SMAP土壤湿度在对数尺度上的密度散点图。由图3可以看出两者的土壤湿度总体上有着良好的一致性,反演所获得的土壤湿度在小于0.35时在1∶1参考线周围数据密集程度较大,但土壤湿度较大时数据密集程度开始下降,反映了线性模型对于较大土壤湿度反演能力的不足。
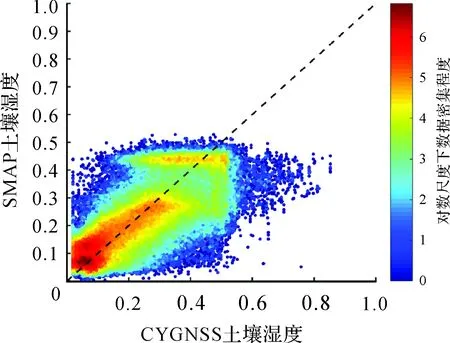
图3 密度散点图Fig.3 Density scatter plot
图4展示了CYGNSS反演土壤湿度与SMAP参考土壤湿度之间的偏差和均方根误差总体统计。可以发现整体的偏差及均方根误差在土壤湿度小于0.35时处于可接受范围内,但两者都会随着土壤湿度大小的增加而增加,当大于一定土壤湿度时产生的误差会过大,这与以往GNSS-R反演风速研究中的问题类似,这可能与作为土壤湿度函数的地表反射率的物理饱和度有关,同时也可能是由于缺乏较大土壤湿度值的训练数据有关[33-34]。这与前面密度散点图中所反映的,随着土壤湿度的增加,CYGNSS土壤湿度数据与SMAP土壤湿度数据对应的密度值下降一致。

图4 偏差和均方根误差统计Fig.4 Bias and root mean square error statistics
为了解决这一问题,本文将线性模型所获取的土壤湿度数据利用提出的阶段函数模型进行处理,以解决对较大土壤湿度区域反演的不确定问题,处理后的误差统计如图5所示。可以看出,反演的误差不再随土壤湿度增大而增大,且对较大土壤湿度区域的反演偏差也限制到了可接受范围。

图5 处理后偏差和均方根误差统计Fig.5 Bias and root mean square error statistics after processing
2.4 全球土壤湿度反演结果分析
通过绘制密度散点图及误差分布图后,可以看出利用神经网络训练所获得的系数解效果在土壤湿度低于一定程度时,是符合要求的,但是对于土壤湿度较高的地方,反演存在一定的误差。而在经过阶段函数模型处理后,反演整体效果大有提升。将线性模型所得数据经本文提出的阶段函数模型处理后,进行全球土壤湿度的反演,以2018年10月25、26、27日3 d的数据为例,绘制全球土壤湿度分布对比图,如图6所示。

图6 全球土壤湿度分布Fig.6 Global distribution of soil moisture
由图6可知,反演得到的土壤湿度在全球范围内与SMAP提供的参考值整体趋势一致,但对于一些土壤湿度较大的区域,如图6中黑框所标记的区域,线性模型反演精度较低,而在使用本文提出的阶段函数模型处理后,对这些区域的土壤湿度反演精度明显得到提升。
为了进一步展示土壤湿度反演效果,笔者绘制了经过两阶段模型处理的土壤湿度反演值与SMAP土壤湿度参考值在全球范围内分布的土壤湿度偏差图(图7)。
由图7可知,在全球范围内,土壤湿度的反演偏差普遍较低,总体反演效果良好,相较于文献[13—14],本文研究范围覆盖了整个热带及亚热带区域,填补了之前研究中数据缺失的区域,基于CYGNSS反演的土壤湿度与SMAP具有良好的一致性,其中对较高土壤湿度区域的反演更精确,总体均方根误差为0.07。但在某些区域,利用GNSS-R反演得到的土壤湿度与参考值之间的差异仍然较大,如图7中的标记区域,引起这些误差的原因可能有以下4个方面:①对异常数据的剔除,本文是根据以往研究的经验,通过筛选信噪比及卫星入射角度来剔除异常数据,但这并不能完全剔除异常数据,仍然会保留一定比例的异常数据,这会影响神经网络模型训练效果,从而影响训练得到的线性模型中各参数的系数解。②地形因素及植被覆盖的影响,这些因素会干扰土壤湿度反演的结果,本文通过加入SMAP提供的植被光学厚度及地面粗糙度信息来解决这个问题,但SMAP提供的辅助数据集是静态的,不能实时反映地面效果,只能在一定程度上减弱植被及地形影响。③GNSS-R数据的精确校准仍然是一个尚未解决的问题,使用接收器增益,发射器范围和接收器范围校准反射率的不确定性与陆地上实际镜面点位置的不确定性直接相关,并与全球导航卫星系统的姿态控制精度相关[35]。④反演模型的问题,本文学习了先前的研究,假设陆面反射由相干反射决定,而在实际中陆面反射可能是相干和非相干混合的,影响了反射率的计算。

图7 全球土壤湿度偏差分布Fig.7 Global distribution of soil moisture bias
2.5 时间序列分析
在全球范围内获取实时的土壤湿度分布后,经过CYGNSS与SMAP土壤湿度数据对比后,可以看出反演模型的整体效果较为理想,而土壤湿度会随着时间变化,这一点对于其他应用的研究也非常重要,因此需要对反演模型的时效性进行评估。本文为了评估模型的时效性效果,利用模型反演得到的土壤湿度进行了时间序列分析。本文使用了2018年10月—2019年5月的CYGNSS数据及SMAP数据,在研究区域内选取地理环境不同的城市为研究对象,以探究模型随时间变化的普适性。分别获取这些研究区域利用CYGNSS数据处理获得的土壤湿度,然后以SMAP提供的土壤湿度作为参考,通过比较两者随时间变化的特征来验证效果,本文以其中位于不同洲的4个城市为例,如图8所示,结果显示CYGNSS土壤湿度无论是随时间产生的变化还是整体的变化趋势,与SMAP土壤湿度是一致的。经过数据处理分析,得到2018年10月—2019年5月全球土壤湿度均方根误差都处于0.07左右,这反映了模型的时效性良好,为以后星载GNSS-R土壤湿度反演技术应用到其他领域提供了保证。

图8 时间序列分析Fig.8 Time series analysis
3 总 结
本文提出了一种基于CYGNSS数据在土壤湿度大于0.35时的星载GNSS-R反演土壤湿度的方法,使用CYGNSS数据处理得到地表反射率,以SMAP提供的温度、植被及地表信息为辅助数据,构造土壤湿度为地表反射率、温度、植被光学厚度及地面粗糙度的线性函数。在利用信噪比等信息剔除了CYGNSS中的噪声数据后,通过神经网络中的线性回归模型来训练线性模型的系数,利用获得的系数求解土壤湿度。对线性模型所获得的土壤湿度以0.35为分界点,再利用本文提出的阶段函数模型进行处理,以实现对不同程度土壤湿度区域更准确的反演。通过将反演结果与SMAP提供的参考土壤湿度对比,结果显示为全球范围内具有良好的一致性。在时间序列分析中,选取全球各大洲的部分城市为研究对象,通过统计各研究区域土壤湿度随时间的变化来评估模型的时效性,结果显示反演得到的土壤湿度随时间变化与参考值较为一致。
——以红沙泉矿区为例

