基于信号强度测距的最小均方误差定位算法*

钱建新 汪味路 杨学明 武江瑞 徐会彬 成新民 张 永

（1.湖州市特种设备检测研究院 湖州 313000）（2.湖州师范学院信息工程学院 湖州 313000）

1 引言

定位算法已成为无线通信领域的研究热点［1～2］。尽管全球定位系统（Global Position System，GPS）在室外区域有较高的定位精度，但是其在室内、地下库等复杂环境下的定位精度很低，难以满足定位精度的要求。

现有的定位算法可分为基于测距和非测距两类。不失一般性，基于测距的定位算法精度高于基于测距定位。在基于测距定位算法中，常利用信号的接收信号强度［3］、到达时间［4］和到达角度等参数测量收/发两端的距离。

此外，由于超宽带信号传输距离短，对信道衰减不敏感，基于超宽带信号测距更适用于室内定位［5］。然而，现多数室内定位算法只考虑了视距（Line-of-Sight，LOS）环境。实际上，在室内环境下，通信链路常处于非视距环境（Non-LOS，NLOS）。不失一般性，多数的室内环境是LOS/NLOS的混合环境。

文献［6～7］针对LOS/NLOS 混合环境，提出稳健统计的节点定位算法。例如，最小中值平方（Least Median squares，LMeds）［8］，M-估计［9～10］是典型的基于稳健统计的定位算法。LMeds 算法采用稳健回归技术（Robust Regression Techniques，RRT）检测NLOS 测量值，并剔除此值，再利用最小中值平方估计未知节点位置。文献［10］针对GPS 定位误差问题，采用Huber M 估计算法减少定位误差，提升定位精度。

此外，利用先验位置信息估计节点位置也是一个常用的定位算法［11］。例如，文献［12］提出基于先验知识的最小均方误差（Minimum Mean Square Error，MMSE）的节点定位算法。该算法利用抽样均值和中值构建误差协方差矩阵，进而最小化加权平方误差（Weighted Square Error，WSE）损失函数。但是，这些算法不能识别LOS/NLOS 混合环境。文献［13］也提出基于权重最小二乘法的节点定位算法。

为此，提出基于信号强度测距的最小均方误差定位（Strength Ranging-based Minimum Mean Square Error localization，SRMSL）算法。SRMSL 算法构建基于超宽带信号的测距模型，再构建基于最小均方误差的定位模型。通过仿真和真实环境分析SRMSL 算法的性能。结果表明，提出的SRMSL算法提高了定位精度，但算法的运算时间偏长。

2 SRMSL算法

2.1 定位模型

UWB 脉冲信号的多径分辨能力强，在短距离测距方面具有独特优势［14］。因此，UWB 脉冲广泛应用于测距领域。

假定在网络内部署N个信标节点，这些节点的位置已知。第i个信标节点的位置标记为si(xi,yi)，且i=0,1,2,…,M-1；x(x,y)表示未知节点的位置（需估计其位置的节点）。

通过测量信号的信号强度值估计发射节点与接收节点间距离。利用式（1）表示信号强度与距离间关系：

式中：i=0,1,2,…,M-1；j=0,1,2,…,N-1，N为总的测量次数；P0表示当参考距离为r0时所接收到的信号强度值，通常取r0=1；γLOS/NLOS表示在LOS/NLOS 两种环境下的路径损耗指数，如图1所示；表示对第i个信标与未知节点间距离的第j次测量值。

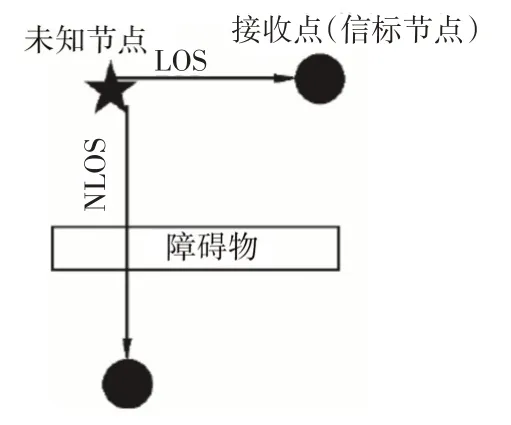
图1 LOS/NLOS环境下的信号传播

在非理想环境下，发射节点与接收节点间的信号受障碍物影响，发生信号衰减。利用对数阴影模型表述信号衰减过程，并对式（1）进行扩展：

当信号传播处于视距环境时，信号能够快速地、小衰减地传输至接收节点；当信号传输处于非视距环境时，如图1 所示［16］，信号的传递可能会障碍物影响，可能会发生反射、绕射，这增加了测距误差。

对等式（4）两边同时平方，可得：

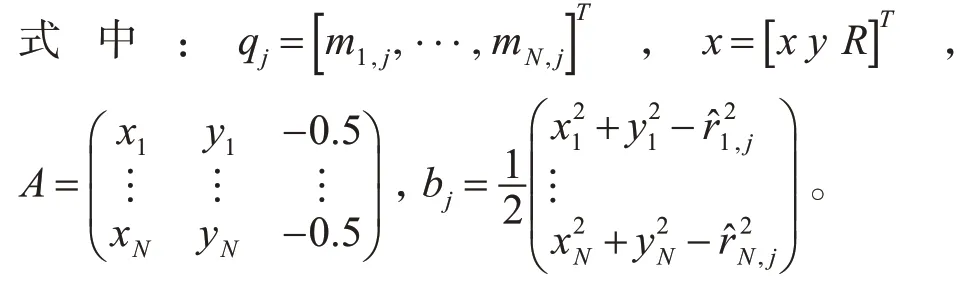
2.2 基于最小均方误差的位置估计

首先，建立最小均方误差等式：

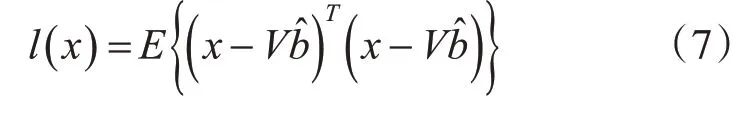
式中：x表示需估计的未知矢量；V表示b的期望值，其定义如式（8）所示：

式中：sgn(·) 表示sign函数。

3 性能分析

3.1 仿真实验

为了有效地分析SRMSL 算法的性能，利用Matlab 软件建立仿真平台。在20m×20m 内分布7个信标节点（N=7）和10 个未知节点。障碍物的位置随机，如图2 所示。图中三角形表示信标节点；小圆圈表示未知节点。

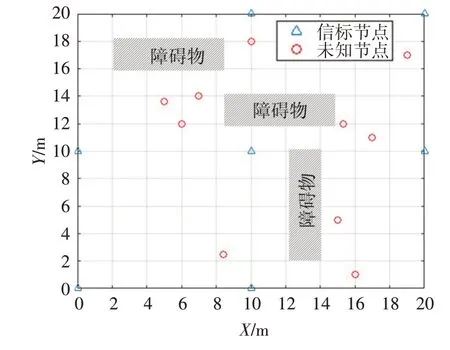
图2 仿真场景

每次仿真独立重复200 次，取平均值作为最终实验数据。选用根均方误差RMSE 作为性能指标，其定义如式（14）所示：

为了更好地分析SRMSL 算法的性能，选择LMeds 估计算法、M 估计（M-EST）［10］和SWLS 算法作为基准算法，对比分析它们的RMSE性能。

3.2 RMSE随ε 的变化情况

图3 给出了ε对RMSE的变化情况，其中μ2=4，σ1=2，σ2=10 。从图可知，ε的增加使RMSE 呈增加趋势。但相比于M-EST 算法、LMeds算法和SWLS 算法，SRMSL 算法控制了RMSE 随ε的增速，在ε的变化期间，SRMSL 算法的RMSE 保持稳定。

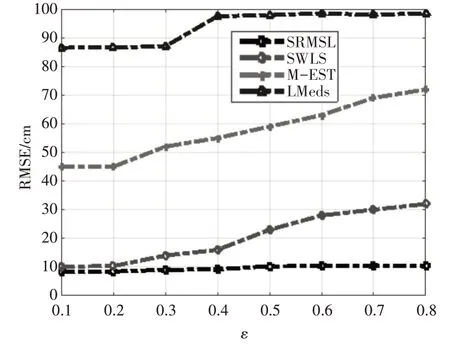
图3 RMSE随ε 的变化情况

3.3 RMSE随σ1 的变化情况

本节分析RMSE 随σ1的变化情况，如图4 所示，其中μ2=4、σ2=10 和ε=0.3 。从图可知，RMSE 随σ1的增加而上升。原因在于：σ1越大，测距误差越大，这不利于测距。相比，相比于M-EST算法、LMeds 算法和SWLS 算法，SRMSL 算法提高了对σ1变化的鲁棒性。

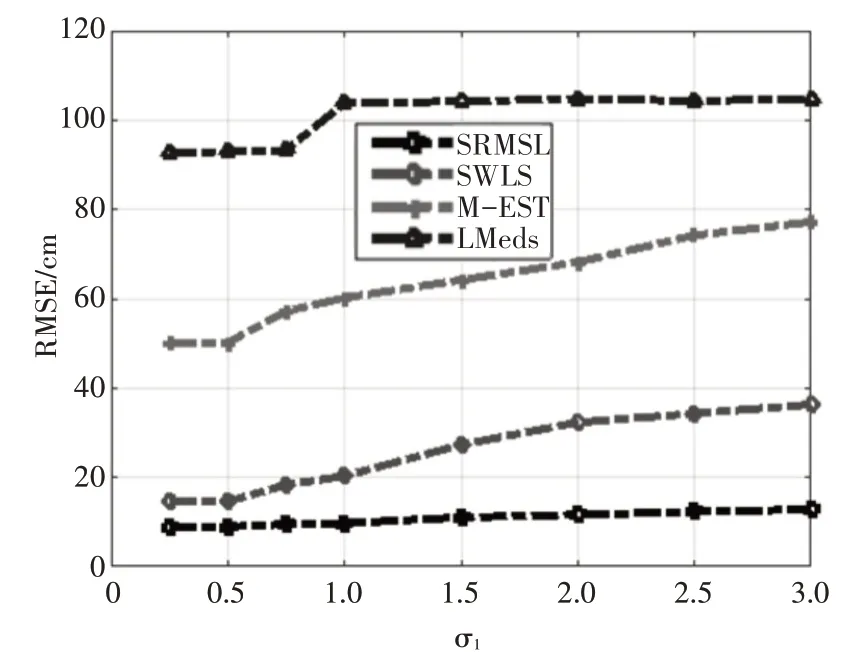
图4 RMSE随σ1 的变化情况

3.4 RMSE随σ2 变化情况

接下来，分析σ2对RMSE 均值的影响，其中σ2从2至10变化，如图5所示。

由图5可知，相比于SWLS算法、M-EST和LMeds算法，SRMSL算法提高了定位精度。原因在于：LMeds 算法只通过最小二乘法估计未知节点位置，未考虑NLOS 场景。由于SWLS 算法是基于LMeds算法的改进算法，降低了定位误差。

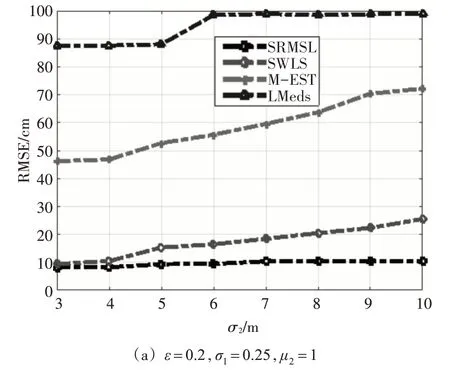
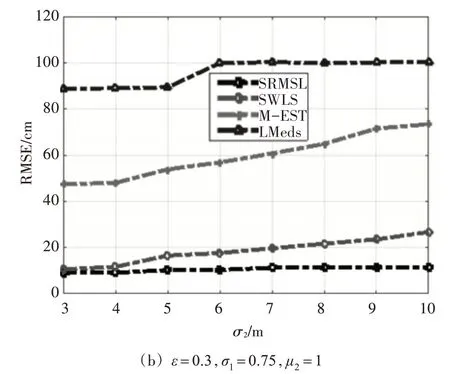
图5 NLOS噪声的标准方差σ2 对A_RMSE 的影响

此外，对比图5（a）和图5（b）不难发现，图5（b）的定位精度劣于图5（a）。这有两个原因：1）增加ε，发生LOS/NLOS 混合场景的概率越大，环境越复杂，测距误差就随之增大；2）增加σ1，测距噪声随之增加，导致测距误差加大。

3.5 真实环境测试

采用UA 100 模块作为信标节点，采用UK 100模块作为未知节点，信标节点与未知节点间存在障碍物，构建一个LOS/NLOS 环境。具体而言，在3m×4m×5m 区域内部署6 个UA 100，5 个UK 100。通过LabVIEW软件与UK 100通信，并在Lab-VIEW 软件上调用定位算法程序，且保证部分通信空间被障碍物阻挡。

表1 给出四个算法的RMSE 性能。从表1 可知，提出的SRMSL 算法将定位误差控制在9cm，而LMeds 算法的RMSE 达到97cm。这说明，提出的SRMSL算法能够有效地提高定位精度。

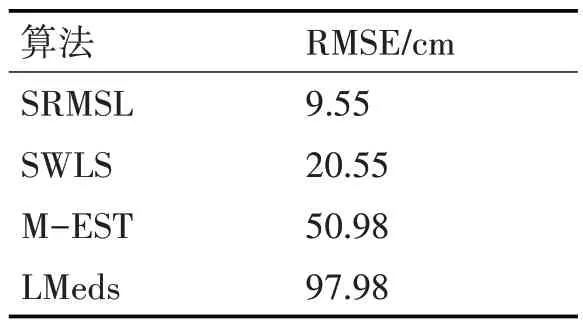
表1 真实环境下的RSME

3.6 算法的复杂度性能

最后，分析算法的复杂度。运行算法的时间越长，算法复杂度越高。电脑参数：Windows 7操作系统、8GB内存，core i7 CPU。利用Matlab 2016a 编写定位算法，并记录运行每个算法所消耗的时间。利用Matlab 软件，编写多个Function 函数，再通过主函数调用实现对定位算法的编程。图6 给出一个Function函数示例。

图6 Function函数示例

为了减少随机误差，独立运行10次，取平均值作为每个算法运行一次所消耗的时间。

表2 给出了SRMSL 算法、SWLS 算法、M-SET算法和LMeds 算法的运算时间。从表2 可知，LMeds 算法的运算时间最低，只有0.7ms。而SRMSL 算法的运算时间达到2.4ms。这说明，SRMSL算法是以高的复杂度换取高的定位精度。

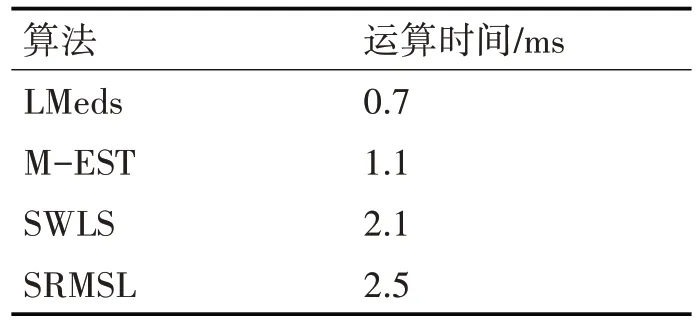
表2 算法的复杂度

4 结语

针对室内环境的定位问题，提出基于信号强度测距的最小均方误差定位（SRMSL）算法。SRMSL算法利用UWB 信号的强的时间分辨能力，估计到达时间，进而测距。再通过MMSE 估计节点位置。同时，考虑到LOS/NLOS 的混合环境，并通过中值函数滤除异常值，减少NLOS 环境对测距精度的影响。

通过仿真和实验分析了SRMSL 算法的定位精度以及算法的复杂性能。结果表明，SRMSL 算法能够提高定位精度，在室内恶劣环境下，定位精度可保持约9cm 水平。但算法的复杂性仍较高。后期，将优化算法，降低算法的复杂度。这将是后期的工作内容。