一种基于改进惯性权重的粒子群优化算法*

钱江波 张佳星 姚大伟 李岩 王巧珍

（华北电力大学 保定 071003）

1 引言

粒子群优化（PSO）算法是Kennedy 等［1］提出的一种基于迭代的进化算法。粒子群优化算法具有需要调整的参数少、编程易实现、收敛速度快等优势，因此被广泛应用于电力系统中的最优潮流计算、机器人路径规划、交通路线规划等领域［2～5］。

但是粒子群算法也有缺点，当适应度函数比较复杂或参数选择不合适时，容易陷入局部收敛，其中惯性权重这一参数对算法的收敛性影响最大。惯性权重比较大时，粒子的全局搜索能力较强，此时收敛速度虽然很快，却不容易得到精确解；惯性权重比较小时，粒子的局部搜索能力强，但是容易陷入局部收敛［5～6］。因此如何寻找一个合适的惯性权重来协调搜索的精度和速度成为当下研究的热点。

针对上述局限性，姜长元等［8］提出了一种惯性权重正弦调整策略；南杰琼等［9］提出了一种改进惯性权值的优化策略，在正弦调整的基础上加入随机扰动因子调整惯性权值；吴静等［10］将差分进化算法与余弦函数结合，进而调整惯性权值；赵志刚等［11］提出了一种随机惯性权重递减策略；武少华等［12］在简化PSO 算法的基础上引入了自适应局部搜索因子，拓宽了搜索范围并提高了搜索精度；姜建国等［13］提出了一种基于余弦的非线性惯性权重递减策略。牛仲新等［14］通过把惯性权值设为由粒子位置、个体最优值和全局最优值影响的参数组，使得每个粒子的每一维度都有其对应的惯性权值参数，提高了计算精度。本文提出了一种非线性递减动态权重策略，并且用四种标准的测试函数作为适应度函数，并与相关文献中的改进粒子群算法进行对比。结果表明改进后算法不仅在精度上有所提升，稳定性也得到了提高。

2 标准粒子群算法

基本PSO算法是根据鸟群觅食规律提出的，核心思想是随机初始化一群没有体积和质量的粒子，把每个粒子看做优化问题的一个可行解，每个粒子在可行解空间内运动，并有一个速度变量决定其方向和距离［15］。在每一次的迭代中，粒子将追随当前最优的粒子pbest，和群体最优值gbest进行搜索，直到满足结束条件。标准PSO 算法则是在基本PSO算法的基础上，通过惯性权重w协调全局搜索和局部搜索能力［7～8］。

式中1 ≤i≤M，c1和c2为学习因子；w为惯性权重；r1和r2为［0-1］范围内的均匀随机数；D为搜索空间的维数，1 ≤d≤D；piD和pgD分别为个体极值和全体极值。

其中标准粒子群算法中惯性权重w的计算公式如下：

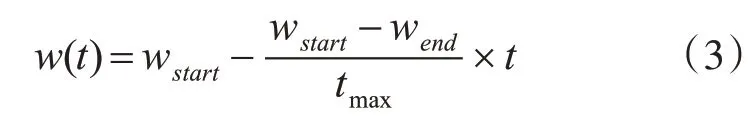
式中wstart为惯性权重的初始值，一般取0.9；wend为迭代结束的惯性权重值，一般取0.4；t为当前迭代次数；tmax为最大迭代次数。

3 改进权重的粒子群算法

针对标准PSO 算法容易陷入局部最优解导致得到的结果准确性不高，难以达到全局最优，文章结合现有的优化算法提出了一种非线性递减权重方法，能够有效平衡局部搜索和全局搜索能力，表示为

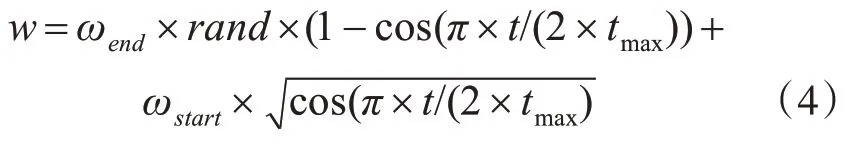
式中wstart、wend、t、tmax的含义同式（3），文章中与其他改进粒子群算法作比较时，取ωstart=0.9，ωend=0.4，tmax=1000。同标准粒子群算法中的线性递减权重相比，改进的惯性权重在迭代初期下降缓慢，从而保持了较好的全局搜索能力，不易陷入局部最优解。在迭代后期惯性权重能够较快的降低，从而保持了算法的局部搜索能力。

改进算法的实现步骤：

1）初始化。设定初始参数，包括最大迭代次数，学习因子，惯性权重的最大值最小值，种群维数和规模；初始化的随机位置xi和速度vi，并且将当前位置记为每个粒子的pi，从所有个体极值中找出全体极值，记为pg。

2）评价粒子。计算粒子的适应度值，如果优于当前个体极值，则将pi设置为该粒子的位置。如果所有个体极值中最优解优于当前的全局极值，则将pg设置为该粒子的位置。

3）粒子的更新。根据式（1）和式（2）更新粒子的速度与位置，当速度超过设定的边界值时取边界值。

4）检验是否符合结束条件。如果当前的迭代次数达到了设定值，或适应度值的增量小于预定的值，则停止迭代，否则跳转步骤2）。

4 仿真验证

为了验证改进后算法的性能，选用了四个标准的测试函数进行检验［16］，并与文献［9］和文献［13］的改进算法进行对比。基本参数设置为：c1、c2均取2，种群数量PopSize取40，种群维数取30，最大迭代次数为500次。

四个测试函数如下：

1）F1：Sphere函数

该函数是非线性的、对称的单峰函数。该函数的全局最优点的函数值F1(x)=0。

2）F2：Rosenbrock函数

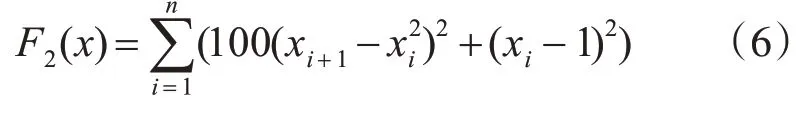
该函数是一个单峰函数，函数变量之间具有很强的相关性，且函数的搜索方向容易受梯度信息的误导，不易找到全局最优。该函数的全局最优点的函数值F2(x)=0。

3）F3：Rastrigin函数

该函数为多峰函数，此函数增加了一个余弦函数来产生大量的最优点。因此在计算时容易陷入局部最优。该函数的全局最优点的函数值F3(x)=0。

4）F4：Griewank 函数

该函数为多峰函数，存在很多局部最小点。由于变量之间具有显著的相关性，因此算法在计算时容易陷入局部最优。该函数的全局最优点的函数F4(x)=0。

对以上四个函数分别用三种不同的算法各运行50 次，并记录不同方法所对应的最大值、最小值、平均值和方差，结果如表1所示。

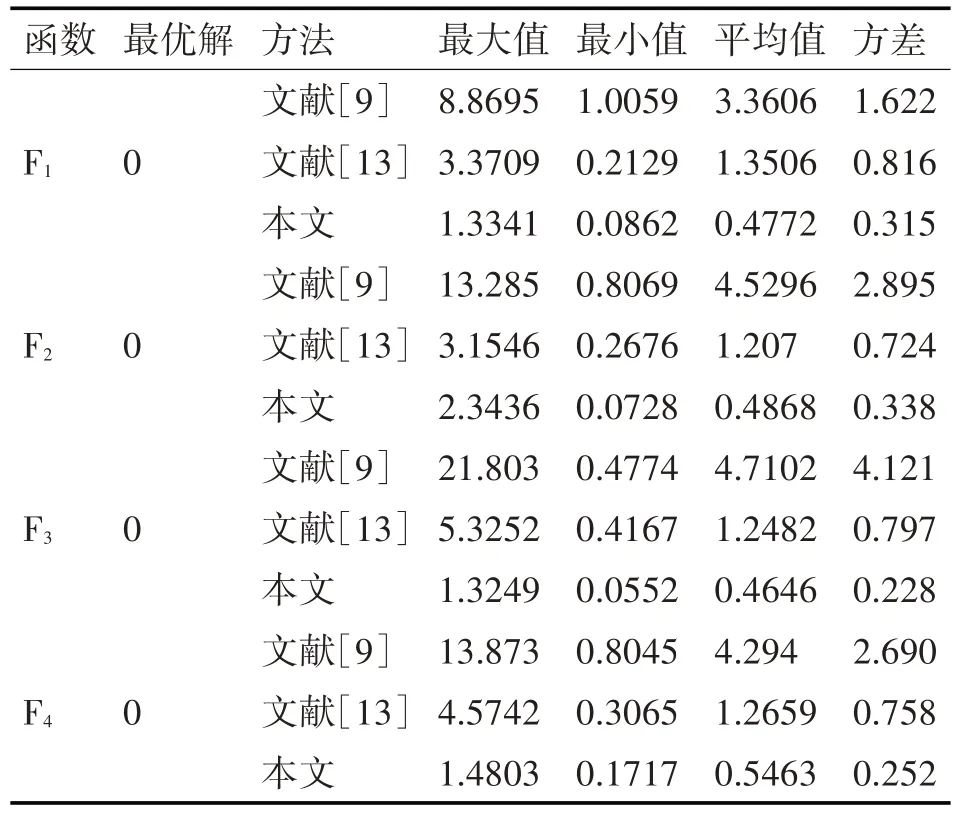
表1 函数测试结果

为了能更加直观地看到对比情况，用Matlab软件将四种函数分别用三种不同算法得到的的最优值变化曲线画出来，如图1～4所示。

图1 Sphere函数最优值变化趋势

从表1 可以看出，用本文的改进方法后测试函数F1、F2、F3和F4的最优值相对于文献［9］和文献［13］的改进算法在精确度上有着明显的提升，更加接近真实值，平均值均有较为明显的下降，且方差也均有明显下降，说明改进后算法的稳定性有着进一步提高。并且同其他两种改进粒子群算法相比，用本文改进后的粒子群算法发现四个测试函数的均值和方差结果相似，误差相对较小，证明了改进是有意义的。

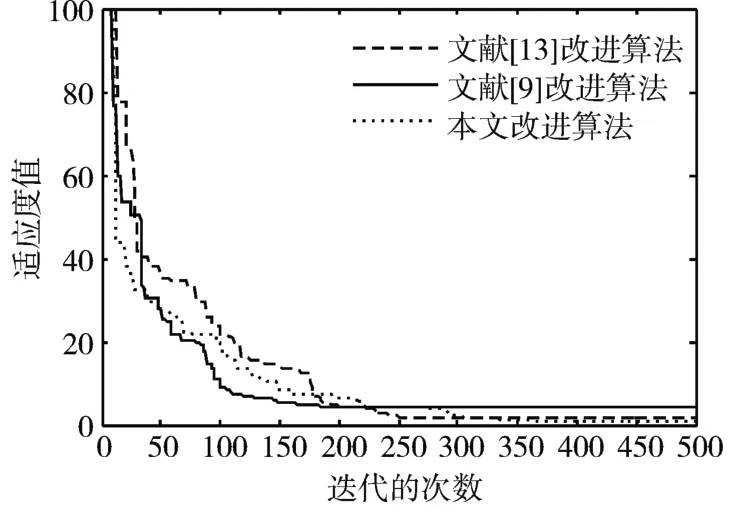
图2 Rosenbrock函数最优值变化趋势

图3 Rastrigin函数最优值变化趋势

图4 Griewank函数最优值变化趋势

通过图1～4 可以看出，本文的改进算法在计算后期曲线有着阶梯状弯曲下降，说明能够在后期更好的避免早熟现象，从而跳出局部收敛。同时通过对图1～3 的观察发现，对于Sphere、Rosenbrock 和Rastrigin 函数文献［9］和文献［13］的收敛时间早于本文改进算法，说明在收敛时间上有待改善。

5 结语

本文通过对标准粒子群算法和其他两种改进粒子群算法的分析，提出了一种新的惯性权重递减策略，并且通过对四种标准测试函数的仿真实验，可以看出提出的改进算法较其他两种算法具有更高的计算精度，较好的算法稳定性。能够更好地跳出局部最优点，避免早熟，计算结果更加接近真实值，具有较好的效果。