基于3D 骨骼数据的课堂个人行为识别研究*

徐苏杰 高尚 张梦坤 朱乐俊

（江苏科技大学 镇江 212003）

1 引言

行为识别一直是计算机视觉中的热门话题，随着人工智能的发展，与人有关的动作行为应用到很多方面，包括视频监控、人机交互、智能驾驶等［1～3］。但是，由于人类行为识别的复杂性，至今依然是一个巨大的挑战。

学生在课堂上的行为表现在课堂教育中有着重要的意义。课堂上学生的行为动作，情绪，注意力，对课堂教育的质量密切相关。识别课堂上学生行为并做出评价是具有重要意义［4～6］。传统课堂的教育评价方式存在既浪费人力又浪费时间，而且效率低的问题，还具有一定的主观性。随着第二代Kinect 传感器的问世，在医学、科研、娱乐等方面的有着越来越广泛的应用。将Kinect 传感器应用到课堂教学当中，是因为该传感器可以获取人体骨骼关节点的三维坐标数据并进行动作行为的识别，Kinect 传感器对光照变化和视角等因素不敏感，具有较高的可利用性。第二代Kinect 传感器可以采集25 个骨骼关节点［7］，如图1 所示，每一个骨骼关节点都有唯一的标示符和对应的三维坐标数据。相比较于传统的RGB 图像识别存在的光照、障碍物遮掩、背景等问题［8～9］，Kinect 传感器的红外摄像头可以捕捉人体的深度图像信息并获取学生的三维坐标数据，Kinect 传感器的4 个麦克风可以采集声音并过滤背景噪声，还可以定位声源，Kinect 传动马达电动机可编程控制仰角，用来获取最佳角度。正是由于Kinect 能准确的描述骨骼数据和计算速度快，并且具有高性价比等优点，越来越受到学者们的追捧，并在人机交互、VR等领域被广泛使用。

图1 人体骨架图

使用Kinect 传感器采集课堂上的骨骼坐标数据并进行识别，不仅可以节省传统课堂教育评价的人力和物力，也可以对光照和障碍物等问题有一定的改善，实现对课堂上的学生行为的精准观察。课堂上学生的消极行为（讲话，睡觉等行为）、交互行为（起立，举手等行为）都会被识别，对提高课堂教学的质量和学生的学习效率有着重要的意义［5，10］。

2 相关工作

2.1 Kinect骨骼数据简介

Kinect 传感器能获取人体动作的彩色图像和深度图像，数据源可以通过Kinect SDK 提供的API来获取25个人体的骨骼关节点坐标数据［11］，如图1所示，依次为臀部中心、脊椎、脖子、头、左肩膀、左手肘、左手腕、左手、右肩膀、右手肘、右手腕、右手、左臀、左膝盖、左脚踝、左脚、右臀、右膝盖、右脚踝、右脚、肩膀、左手尖、左拇指、右手键、右拇指，这些骨骼关节点就是下文中用到的姿势特征点。

2.2 骨骼动作识别方法

基于骨骼的动作识别方法现分为两大类：一是基于深度学习，二是基于手动特征提取。基于深度学习是通过使用深度学习的方法自身学习，提取特征，这种动作识别方法需要大量的训练数据，花费时间长，优点是准确率高。基于手动特征提取的方法是通过人工的方式提取特征，然后对特征进行建模并使用分类器进行分类比较。手动提取特征的方法耗费大量的人力，对于数据量规模不是很大的数据集来说，计算量较小并且精准度能满足要求。

基于手动特征提取的方法可以根据描述符的性质分为四类［12］。

2.2.1 基于位置的描述符

基于位置的描述符是直接使用关节位置来构建描述符。Jiang 等［13］使用傅立叶时间金字塔（FTP）对各关节与其他关节的相对成对位置来表示骨架序列的每一帧进行建模。Yang 等［14］提出了局部特征方法来建立局部特征矩阵，实现多种特征的融合和降维。但是这种方法忽略了人与环境，人与人等之间的交互信息，只专注于局部特征，比如打电话和举手，忽略了场景的信息，大大增加了歧义性。

2.2.2 基于几何的描述符

基于几何的描述符是通过几何概念来表示骨骼运动。Arrate 等［15］提出利用在不同身体部位之间的旋转和平移来表示三维几何模型关系，将人体骨骼表示Lie 群中的点，整个人体骨骼为SE（3）×…×SE（3），利用DTW 和傅里叶时间金字塔做数据处理，然后进行建模和分类。Chen 等［16］提出GPD（Geometric Pose Descriptor）特征，该特征利用关节点的空间位置和距离等信息来描述人体的运动状态。

2.2.3 基于运动的描述符

基于运动的描述符是通过关节运动学来描述的，如速度，加速度和距离等。Leordeanu 等［17］提出串联这些特征，然后加权，最后通过KNN 算法进行分类。Boutteau 等［18］KSC 特征描述符，这个描述符是位置，速度和加速度这一些运动学实体来建立的。

2.2.4 基于统计的描述符

基于统计的描述符利用统计工具来表示有区别的动作。Koniusz 等［19］提出了使用核张量的方法来记录两个动作序列之间的兼容性和每个动作的动态信息。Tang 等［20］提出利用加权协方差的描述符的方法实时积累信息和在线预测。

3 本文方法

3.1 特征提取

人体骨骼模型中有n个关节点，给定一个髋关节点，可以求得其他n-1 个关节点与髋关节点的欧式距离和夹角余弦值。数据集中的视频一秒大概30 帧左右，给定每一秒钟的第一帧，可以求得其他每一帧的关节点与第一帧关节点的欧式距离和夹角的余弦值。

3.1.1 距离特征

假设有n个关节点构成的骨骼数据，在t帧下的第i个关节点的坐标可以表示为：Ji(t)={xi(t),yi(t),zi(t)}(1≤i≤n)，则第t帧下的骨骼状态为：St={J1(t),J2(t)…Jn(t)}，对于给定N帧的动作序列就可以表示为v=(S1,S2,…SN)。其中第三个关节点表示髋关节坐标{x3(t),y3(t),z3(t)}，即则第t帧下第i个和髋关节点间的欧式距离为式（1）。

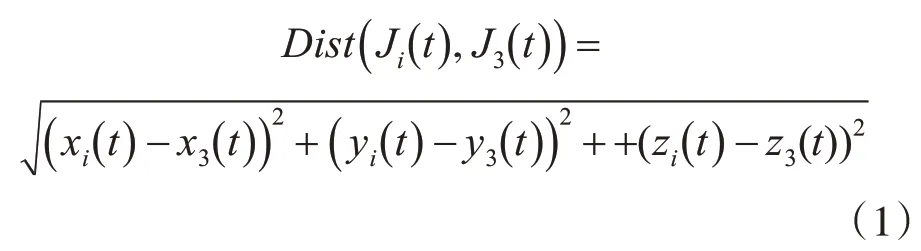
人体的行为动作不仅与人当前的位置信息有关，还与过去的位置信息相关，所以我们不仅要将当前帧的骨骼特征表示出来，还要将当前帧与初始帧对应的骨骼特征表示出来。所以第t帧下第i个关节点和第1帧下第i个关节点间的欧式距离为式（2）：

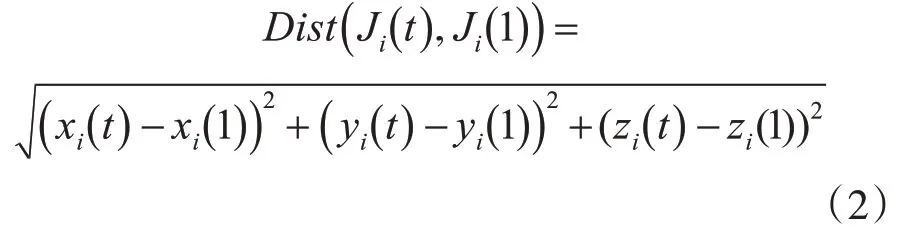
3.1.2 角度特征

假设一个人体骨骼数据，因为，人体骨骼关节点存在角度关系，且骨骼关节点的角度会随着人体运动而发生变化，所以确定人体骨骼关节点的三维坐标位置，就能计算各个关节点之间的夹角。第t帧下第i个关节点和髋关节点间的夹角余弦值的式（3）：

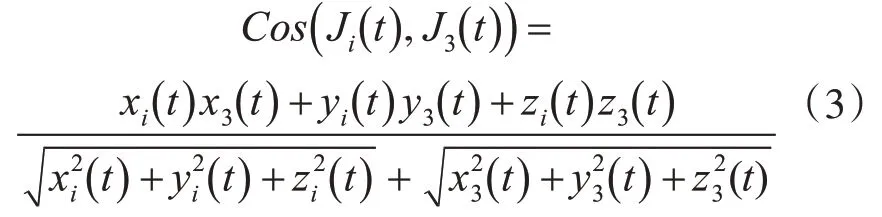
第t帧下第i个关节点和第1 帧下第i个关节点间的夹角余弦值的式（4）：

3.2 数据降维

本文中利用到4 个特征向量，所以特征向量的维度较高，维度很高的话会存在一些冗余的信息和噪音信息，在接下来的建模和分类中会造成误差，降低准确率。PCA 降维的主要思想是将可能具有相关性的高维变量合成线性无关的低维变量，计算公式为

其中y 为主成分特征，xi是需要降维的特征，xˉ是特征均值，UT是协方差矩阵计算矩阵，计算公式为

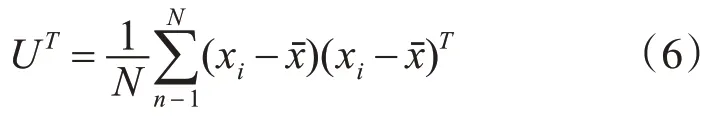
3.3 分类器

3.3.1 SVM

支持向量机（SVM）的基本思想是能够正确的划分训练数据集并几何间隔最大的分离超平面。SVM适合小量样本数据，可以利用内积核函数代替向高维空间的非线性映射。因此本文选用SVM 分类器对骨骼数据进行分类。

SVM的目标函数为

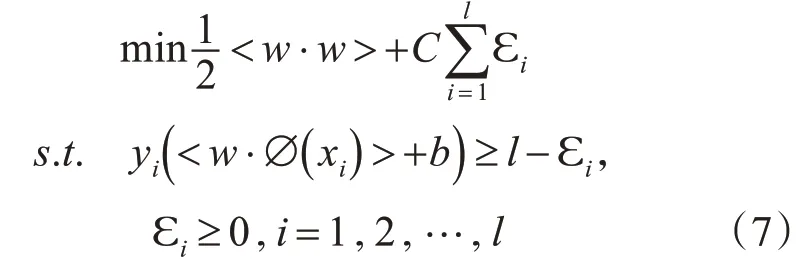
其对偶问题为

则分类函数为

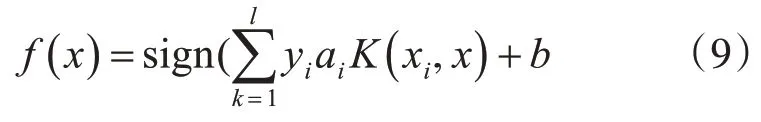
其中，（xi,yi）为训练样本，xi和yi分别是样本的特征向量和标签类；l为训练的样本数量；ℇi是松弛变量；C为惩罚系数，是对误差的宽容度，C越高，容易过拟合。C越小，容易欠拟合。

3.3.2 核函数

支持向量机（SVM）是一种用于处理线性可分的分类算法，对于处理非线性可分的数据时，SVM先在低维的空间中完成计算，利用核函数映射到高维特征空间，构造出最优分离超平面，将非线性数据分开。

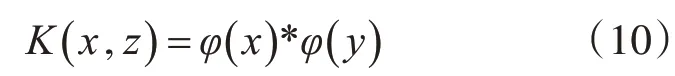
式（10）中函数K(x,z)为核函数（Kernal Function），常用的核函数有线性核函数、多项式核函数和径向基核函数还有Sigmoid核函数。

1）线性核函数：

2）多项式核函数：

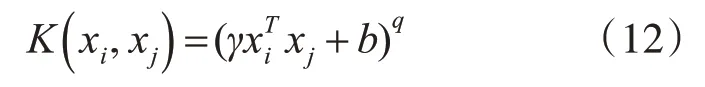
多项式核中，需要指定的参数为核函数参数γ，b以及q。

3）径向基核函数：

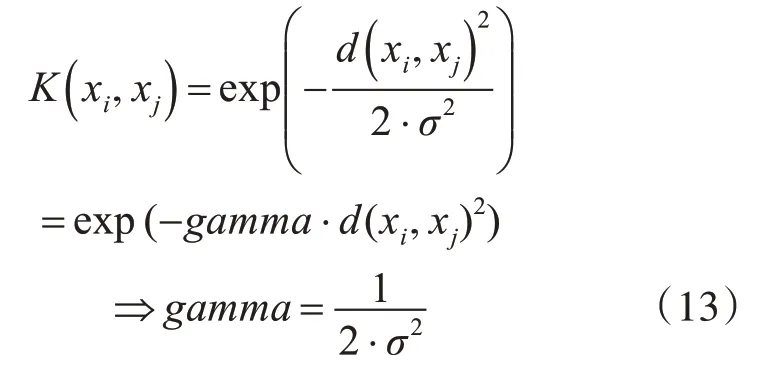
若选择径向基核作为Kernel，该函数会自带一个gamma参数，gamma参数和σ2的关系如式（13）。

4）Sigmoid核函数：

Sigmoid核中，需要指定的参数为γ。

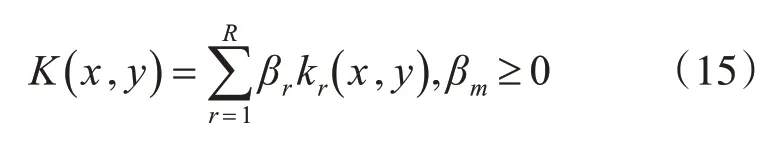
其中βm为子核函数的权值，满足：

在实验中，选择了高斯核函数，多项式核函数和Sigmoid核函数作为多核核函数的子核函数。

4 实验结果

4.1 实验环境

实验在配置为Inter（R）Core（TM）i5-4200H CPU2.8GHz，12GB 内存，64 位操作系统的个人电脑上进行。

4.2 数据集

本文选取三个公测数据集和实测数据集分别对文中所提方法进行有效性验证。其中三个公测数据集分别为：Florence3D-Action，UTKinect-Action和MSR-Action3D。

1）UTKinect-Action 数据集：该数据集有10 个动作，10个测试者，每个测试者执行每个动作2次，总共有199个深度序列图。

2）Florence3D-Action 数据集：该数据集有9 个动作，10 个测试者，每个测试者执行每个动作2～3次，总共有215个深度序列图。

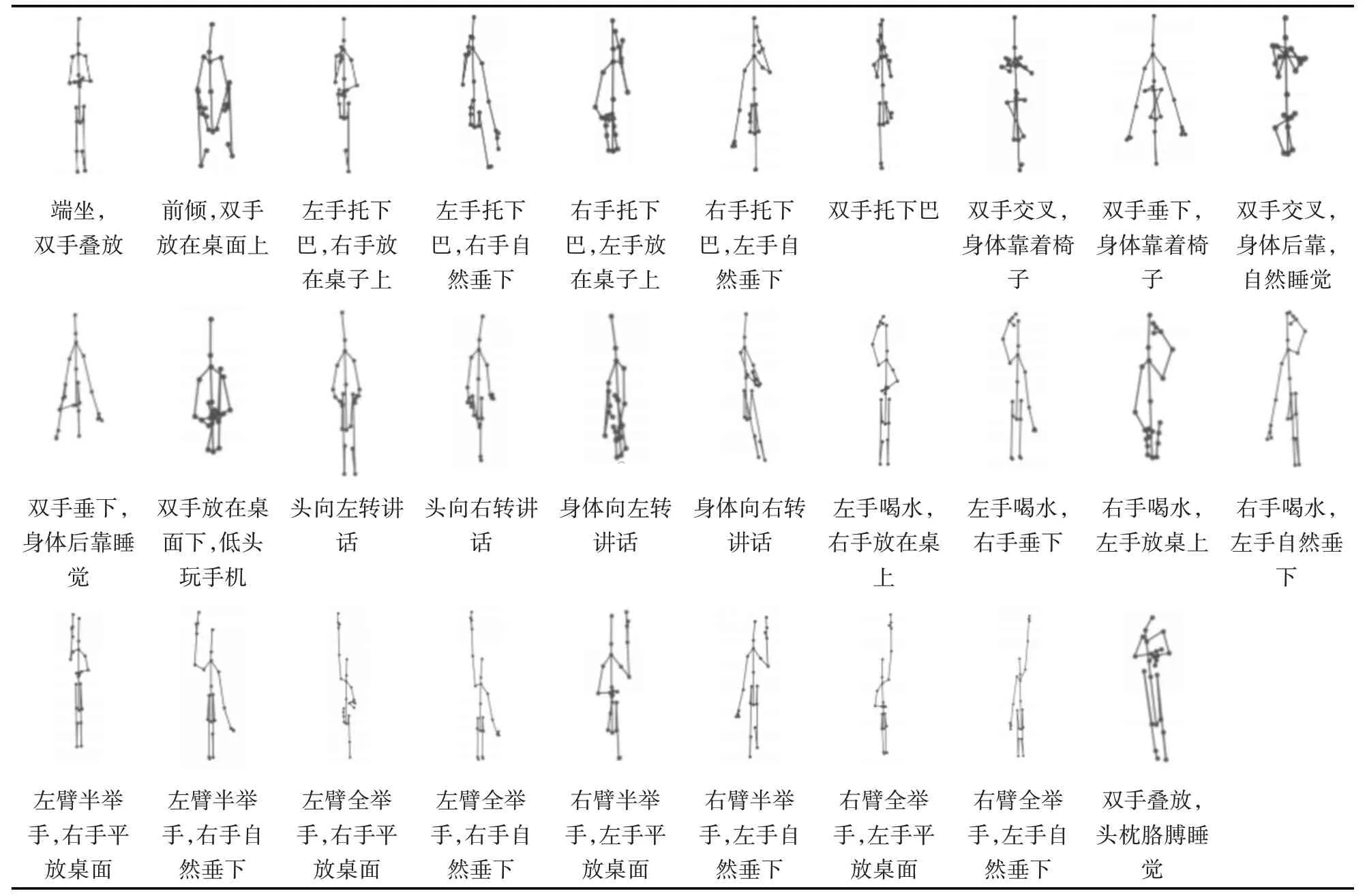
表1 采集的29个动作的骨骼图像

3）MSR-Action3D 数据集：该数据集使用类似于Kinect 的深度传感器捕获。该数据集有20 个动作，10 个不同的测试者，每个测试者执行每个动作2～3次，总共有567个深度图序列。

4.3 对比方法及性能指标

实验中4 个数据集随机选取1/2 的数据集作为训练样本，其余作为测试样本。这里选择的提取方法是Joint angles 方法、Joint positions 方法，和基于深度学习网络的ST-GCN［21］方法作为对比实验方法。本论文设置高斯核函数权值β1=0.5，多项式核函数和Sigmoid 核函数权值分别为β2=β3=0.25。实验结果如表2所示。

表2 MSRAction3D数据集实验结果

从MSRAction3D 数据集中，我们可以看到在AS1，AS2数据集上，我们的方法可以实现更高的准确率，但是在AS3 数据集上，基于手工特征方法的Joint positions方法准确率最高。AS3中的数据都是复杂性较高的动作，所以可以看出，我们的方法不适用于复杂性较高的动作识别。

从表3、表4、表5 可以看出我们的方法可以实现更高的准确率，尤其是在我们的课堂实测数据集上。对于基于深度学习网络的ST-GCN 方法中，准确率普遍偏低，说明在训练数据不充足的情况下，计算机无法学习出更好的特征。在课堂行为数据集上，多核SVM分类器准确率达到0.947，明显优于其他基于手工特征的对比方法。

表3 Florence3D数据集实验结果

表4 UTKinect数据集实验结果

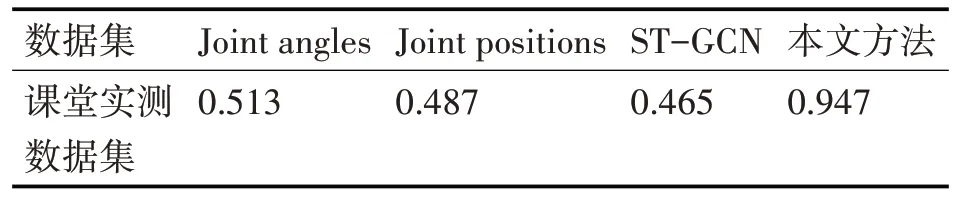
表5 课堂实测数据集实验结果

5 结语

通过采集学生在课堂上的行为数据并进行分析，可以为教学形成有效的教学反馈，提高学生的学习效率。通过获取到学生在课堂上的三维骨骼数据，再对骨骼关节点的距离和角度特征，采用多核SVM 非线性分类器进行行为识别。从实验结果可以看出，基于距离和角度的方法可以在公测和实测数据集上有很好的准确率。但是实验中的维度较高，所以在后期可以通过一定的算法，通过选择一定合适的维度进行降维。虽然基于多核的SVM具有很好的识别率，但是未来我们可以自动学习核函数适合的权值参数。