基于小样本学习的物联网异常状态修正算法
燕 敏,阮秀琴,赵 阳,郑宏涛
(1. 西安石油大学信息中心,陕西 西安 710065;2. 西安理工大学信息化管理处,陕西 西安 710048)
1 引言
物联网主要由感知层、网络层与应用层构成。其中,感知层位于物联网的最底层,包含多种传感器与控制器,是物联网信息采集的关键组件[1-2]。感知层返回的数据是物联网决策的根本依据,也决定着物联网状态的好坏。通过研究可知,物联网异常状态主要包含两个因素,其一是外界干扰破坏与复杂部署环境的影响,导致物联网节点软、硬件发生故障或者消耗大量能源,致使物联网状态异常;其二是物联网节点部署环境区域发生特定事件。如何精准的修正物联网异常状态,成为现今物联网应用领域重点研究课题之一。
物联网异常状态检测需具备一定的特征,要求时间与空间复杂程度较低,但在现有物联网异常状态算法检测过程中,大多数利用时空相关性原理,其导致现有算法存在着修正正确率低下、算法时延较长等缺陷,故提出基于小样本学习的物联网异常状态修正算法研究。小样本学习为模型训练阶段只需要一个或者多个已标记的训练样本,能够降低计算的过程,有利用提升算法的修正正确率,减少算法的时延,为物联网的稳定运行提供更加有效的保障。
2 物联网异常状态修正算法
2.1 相关性特征小样本获取
为精确检测与修正物联网异常状态,获取物联网异常状态小样本为关键,即物联网异常状态特征,可以反映出物联网异常状态下局部差异性信息[3]。根据物联网节点互相关系数,获取物联网异常节点空间相关性特征,具体过程如下。
物联网节点互相关系数运算如图1所示。
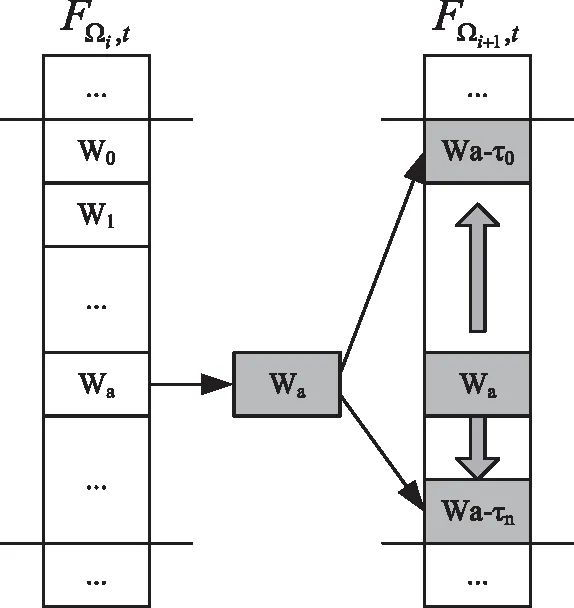
图1 物联网节点互相关系数运算
如图1所示,Ωi为物联网某一节点;Ωi+1为利用空间物理距离寻找出与Ωi距离最近的节点;FΩi,t与FΩi+1,t为设置观测时间序列。

通过上述两个观测时间序列之间的互相关运算获取节点Ωi关于节点Ωi+1的互相关系数,计算公式为
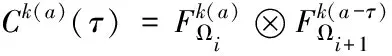
(1)
式(1)中,Ck(a)(τ)表示的是节点之间的互相关系数;⊗表示的是计算规则。
依据式(1)获取的节点互相关系数Ck(a)(τ),提取物联网节点的空间相关特征。以式(1)为基础,得到节点互相关系数Ck(a)(τ)与时延τ的变化曲线如图2所示。
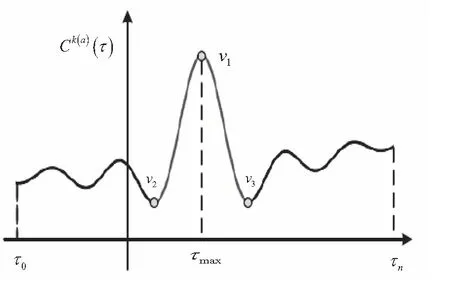
图2 节点互相关系数Ck(a)(τ)与时延τ变化曲线图

将上述三个几何特征作为物联网节点的一组空间相关特征φ(x),反映节点与相近节点的空间相关程度,将其作为物联网异常状态小样本,以此为依据来反映物联网异常状态的局部差异性信息。
2.2 小样本度量学习
以上述获取的物联网异常状态小样本为基础,采用欧式度量方法完成小样本学习,为后续小样本学习网络搭建做准备[6]。
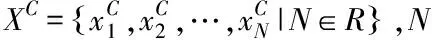

(2)
以式(2)的结果作为类原型,用于表示物联网异常状态类别。
欧式度量方法可以直接在特征空间上计算物联网节点距离,计算公式为
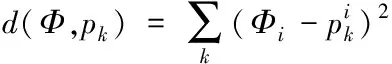
(3)
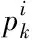
采用softmax对式(3)结果进行相应处理,以此来降低向量中异常值对向量的影响,处理公式为
(4)
式(4)中,k表示的是类别数量。
通过softmax处理后,物联网节点距离数值范围被归一化为[0,1]。若式(4)结果越大,表明物联网异常状态类型属于对应类别的概率越大。
2.3 小样本学习网络搭建
以上述小样本度量学习结果为基础,搭建小样本学习网络,获取物联网异常状态检测结果,为最终物联网异常状态修正做基础[8]。
小样本学习网络具备明显的block结构,每个block结构均包含归一化层、卷积层、池化层与激活层[9]。为更加精准的检测与修正物联网异常状态,对小样本学习网络参数进行详细设置,具体如表1所示。
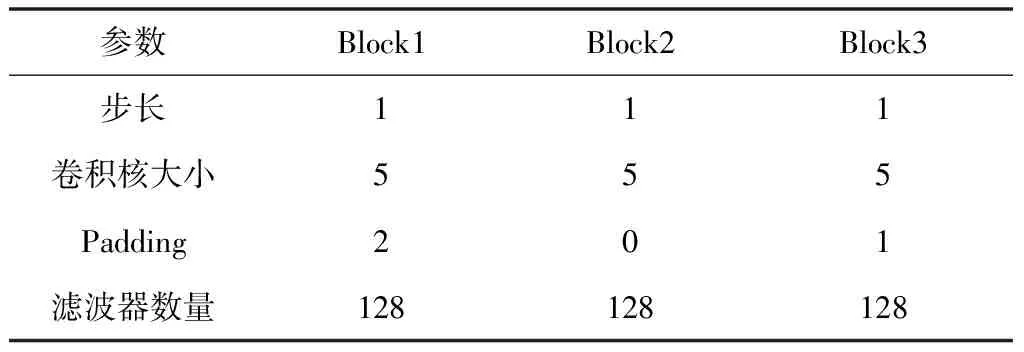
表1 小样本学习网络参数设置表
为使小样本学习网络能够学习到泛化性较好的参数,将距离损失表示为
arg min-lgΦk(y=k|x)
(5)
式(5)中,Φk(y=k|x)由式(4)中的样本x是标签为k的样本概率。
以式(5)结果构建任务迭代最小化目标函数,通过一定次数的迭代,获得最佳泛化性的网络参数。
2.4 物联网异常状态修正的实现
以上述搭建的小样本学习网络为依据,执行小样本学习算法获取物联网异常状态数据,利用RBF神经网络修正物联网异常状态数据,具体修正过程如下所示:
RBF神经网络是基于函数逼近理论构建的前馈性网络,其结构为三层,包含输入层、隐含层与输出层。将物联网异常状态数据作为RBF神经网络的输入量,RBF神经网络的输出量即为异常状态修正数值[10]。RBF神经网络输出结果表示为
(6)
式(6)中,y表示的是RBF神经网络输出量;n表示的是输入层节点数量;ωi表示的是隐含层第i个节点与输出层之间的权值;Ri(x)表示的是隐含层第i个径向基函数;x=[x1,x2,…,xn]T表示的是RBF神经网络输入量。
为了保障物联网异常状态数据的修正精度,确定RBF神经网络各层节点数量及其相关参数。
其中,输入层节点数量由输入数据维数确定,而输出层数值为修正数据,故节点数量为1。隐含层节点数量决定着模型的运行效率,故利用试凑法来确定其节点数量[11]。
径向基函数决定着模型的修正准确程度,选取高斯函数作为径向基函数,表达式为

(7)
RBF神经网络修正模型训练结构如图3所示。
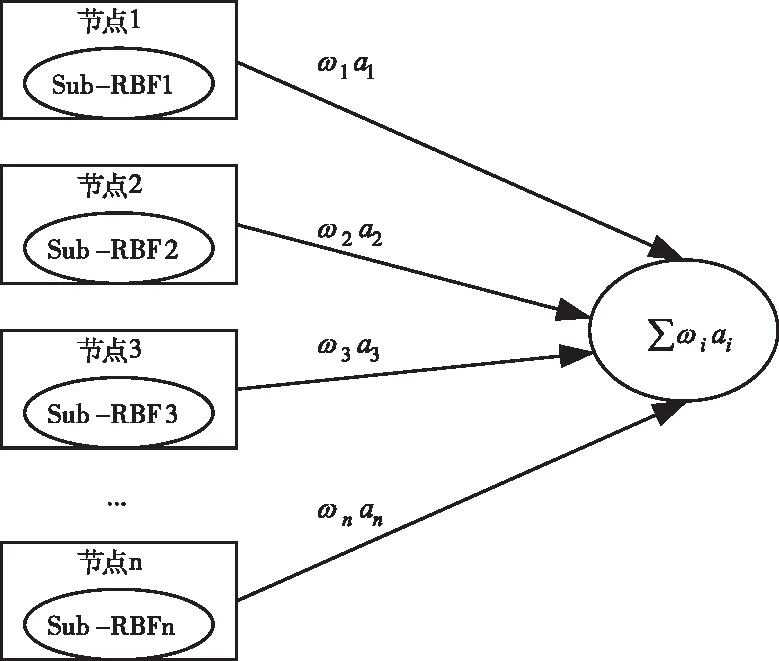
图3 RBF神经网络修正模型训练结构图
如图3所示,ωi表示的是隐含层节点与输出层之间的权值向量;ai表示的是每个节点在模型集群中占据的比重。
在确定RBF神经网络各层节点数量及其相关参数基础上,进行物联网异常状态数据修正,其步骤如下:
步骤一:构建RBF神经网络修正模型,将其模型结构设置为多输入单输出形式[12]。加载物联网异常状态数据,将其作为RBF神经网络修正模型的输入;
步骤二:构建训练样本,并对其进行归一化处理,接着对训练样本进行划分,将其分布至不同网络节点上,同时对模型进行训练;
步骤三:经过步骤二的训练,将输入量输入RBF神经网络修正模型,获得一组对应的输出值,将其作为异常状态数据;
步骤四:在物联网异常状态修正后,通过相对误差确定修正效果。相对误差计算公式为
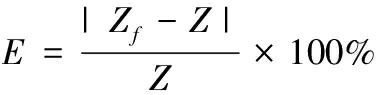
(8)
式(8)中,Zf表示的是修正后物联网状态数据;Z表示的是原始物联网异常状态数据。
通过上述过程实现物联网异常状态的修正,减少物联网异常状态修正的时间,为物联网的应用与运行提供更加有效的保障。
3 实验与结果分析
为验证提出算法与现有算法的性能差异,采用MATLAB软件设计仿真对比实验,具体实验过程如下:
3.1 实验准备
为保障实验的顺利进行,对实验数据、参数等进行充分准备。实验采用3.10GHz的Intel Core与Windows 7操作系统作为实验硬件、软件环境。
现今,国内并没有通用的物联网数据集,并且获取大量数据的物联网运行数据难度较大。为此,利用仿真序列产生器,产生物联网异常状态数据,并将其存储在文档中,供仿真使用。
仿真序列产生器产生的物联网异常状态数据波动与真实物联网异常状态数据波动情况如图4所示。

图4 仿真数据与真实数据的一致性对比
如图4所示,仿真序列产生器产生的物联网异常状态数据波动方差与真实物联网异常状态数据波动方差具有一致性,说明本次仿真所得数据具有较高精度,为后续实验结果的准确做基础。
3.2 实验结果分析
依据上述实验准备数据进行物联网异常状态修正仿真,通过修正正确率以及算法时延反映算法性能,具体实验结果分析过程如下:
3.2.1 修正正确率分析
为得到客观的实验结论,分别在物联网异常状态程度10%与60%背景下进行仿真,得到异常状态修正正确率数据如表2、表3所示。
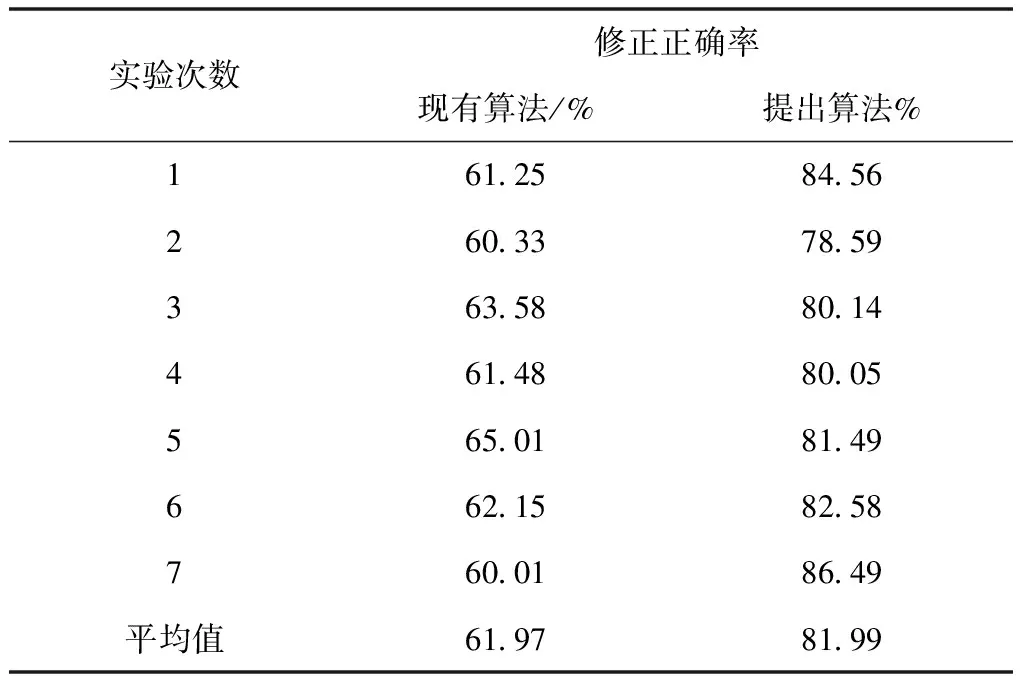
表2 物联网异常状态程度10%背景下不同算法修正正确率数据表
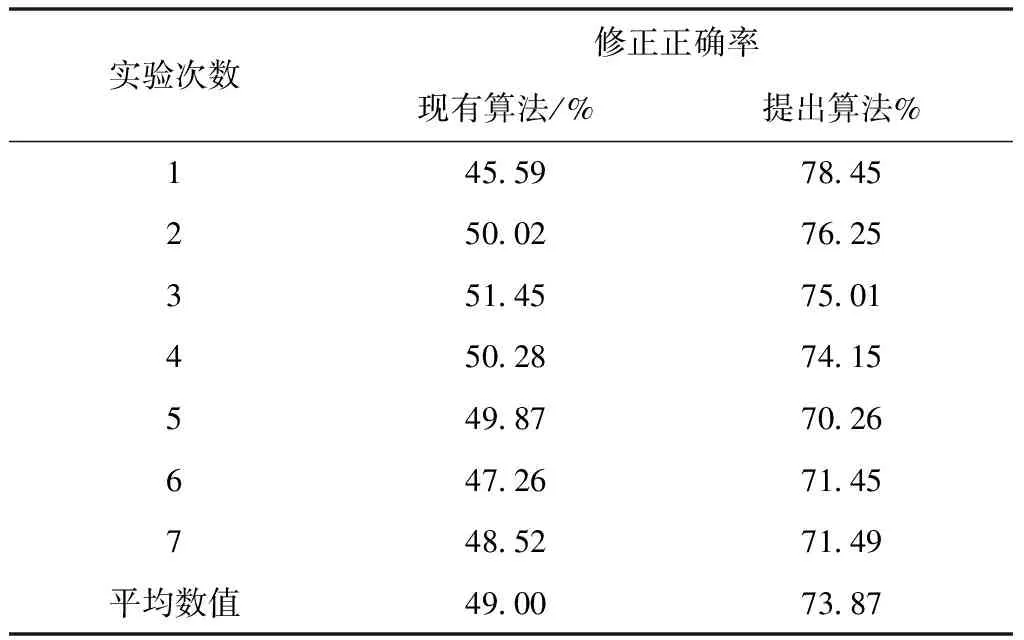
表3 物联网异常状态程度60%背景下不同算法修正正确率数据表
如表2和表3数据显示,随着物联网异常状态程度的增加,算法修正正确率呈现下降的趋势。与现有算法相比较,提出算法修正正确率更加稳定与一致。以修正正确率平均数值为依据,与现有算法数据相比较,提出算法在物联网异常状态程度10%背景下,修正正确率平均数值上升了20.02%;在物联网异常状态程度60%背景下,修正正确率平均数值上升了24.87%。
3.2.2 算法时延分析
算法时延为物联网异常状态修正的时间长短。在物联网异常状态程度10%与60%背景下,得到算法时延数据如表4、表5所示。
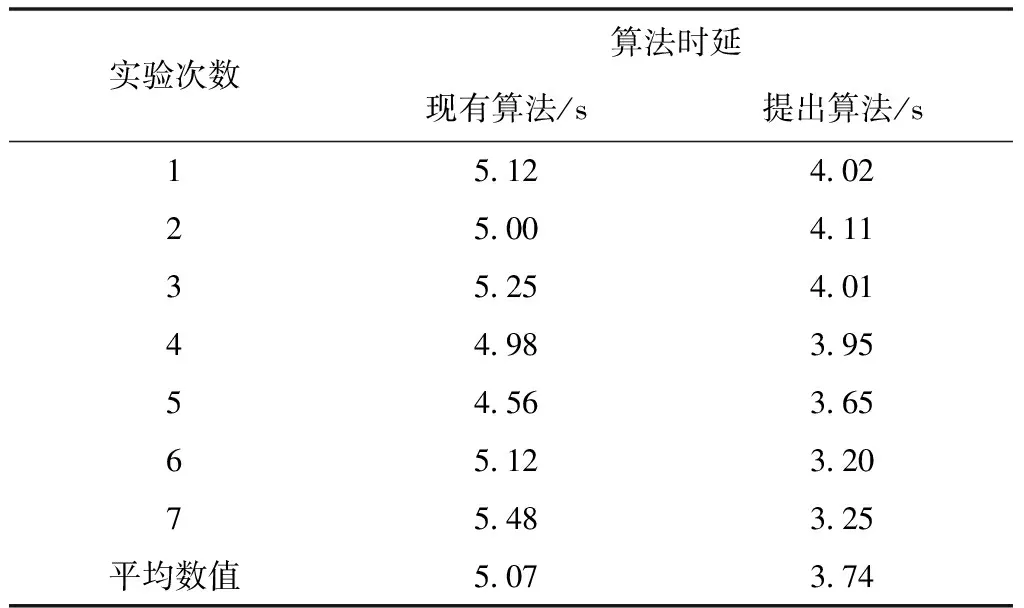
表4 物联网异常状态程度10%背景下不同算法时延数据表
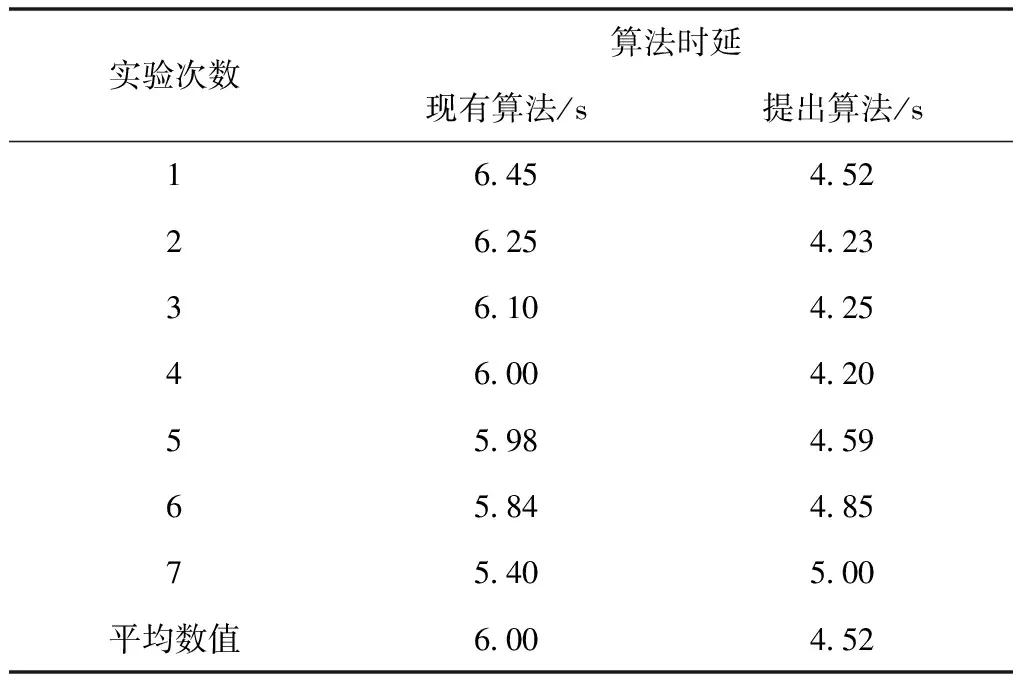
表5 物联网异常状态程度60%背景下不同算法时延数据表
如表4、表5数据显示,随着物联网异常状态程度的增加,算法时延呈现上升的趋势。以算法时延平均数值为依据,与现有算法数据相比较,提出算法在物联网异常状态程度10%背景下,算法时延平均数值下降了1.33s;在物联网异常状态程度60%背景下,算法时延平均数值下降了1.48s。
上述实验结果显示:与现有算法相比较,提出算法修正正确率更高、算法时延更短,充分说明提出算法的修正性能更好。
4 结束语
本文基于小样本学习提出新的物联网异常状态修正算法。实验验证了该算法提升了修正正确率,缩短了算法时延,为物联网的稳定运行提供更加有效的保障。

