测控设备噪声功率高效控制优化方法仿真
冀虹光,杨辉华
(1. 北京邮电大学现代邮政学院(自动化学院),北京 100876;2. 北京邮电大学人工智能学院,北京 100876)
1 引言
随着科学技术和互联网技术的飞速发展,不同工作领域产生的噪声引起了社会各界学者的高度重视,噪声的存在会对人类的生产生活以及身心健康产生比较严重的影响,同时还会对机器设备产生负面影响,导致设备无法正常运行,严重危害设备的使用寿命。为了更好地解决上述问题,相关专家针对智能测控设备噪声功率自适应控制技术进行了大量的研究[1,2],并取得了比较不错的研究的研究成果。例如刘觉夫等人[3]在满足主用户和其他用户正常通信交流的条件下,将信道状态对应的概念全部应用到效用函数中,增强对系统中理性用户的自私性惩罚,确保噪声功率得到有效控制。张启军[4]分析发动机万有特性曲线,将转速和负载两者进行科学合理地匹配,通过匹配结果有效实现降噪控制。上述已有控制方法未能对设备中存在的噪声进行识别,导致稳态误差增加,控制结果不理想,同时音质质量降低。提出一种数字化智能测控设备噪声功率自适应控制方法,仿真结果表明,所提方法能够全面提升音质质量,降低稳态误差,获取满意的噪声功率自适应控制结果。
2 噪声功率自适应控制方法
2.1 数字化智能测控设备噪声识别
利用图1给出数字化智能测控设备噪声识别的具体操作流程图。

图1 数字化智能测控设备噪声识别流程图
数字化智能测控设备噪声识别主要划分为两个不同的阶段:①异常噪声特征提取,需要借助传感器完成数字化智能测控设备的声音采集[5,6],但是在实际操作的过程中存在频谱泄露问题,需要利用Hannning自卷积窗替换Hannning窗和Mel滤波器,得到HSCW-MFCC作为数字化智能测控设备异常噪声特征值,同时将其输入到SVM中进行模式识别[7,8]。②第二阶段为模式识别。
当声频感知高于1000Hz时,会呈非线性。为了更好地描述语音信号,在对其进行处理的过程中,主要通过Mel标度进行描述。利用式(1)给出感知频率和实际频率两者之间的近似关系

(1)
式中,FMel代表感知频率,单位为Mel;f代表实际频率,单位为Hz。
Mel倒频谱系数分析方法主要是通过非线性划分方法对获取的频谱特征进行计算。其中,在语音信号预处理阶段,需要通过Hanning窗截取重要的音频信息。但是在实际操作的过程中,会存在比较严重的频谱泄露问题,同时也无法精准反映数字化智能测控设备中的音频信息。当数据被截取,则说明频率一定会被泄露,导致各个窗函数对于频谱泄露的抑制效果也存在十分明显的差异,需要针对实际环境选择符合条件的窗函数。
分别对比HSCW窗和Hanning窗频谱特征,其中数据长度为M的二阶HSCW窗频域W2(ω)计算式如下

(2)
式中,WR(ω)代表数字化智能测控设备的窗频率响应曲线;e代表数据点的数量;j代表旁瓣的衰减速率。
通过上述分析能够获取两种不同窗函数的旁瓣性能。经过对其分析可知,HSCW窗对频谱泄露的抑制效果明显优于Hanning窗,同时对异常噪声提取的准确率也明显更高一些。
利用图2详细给出MFCC参数的具体提取流程。
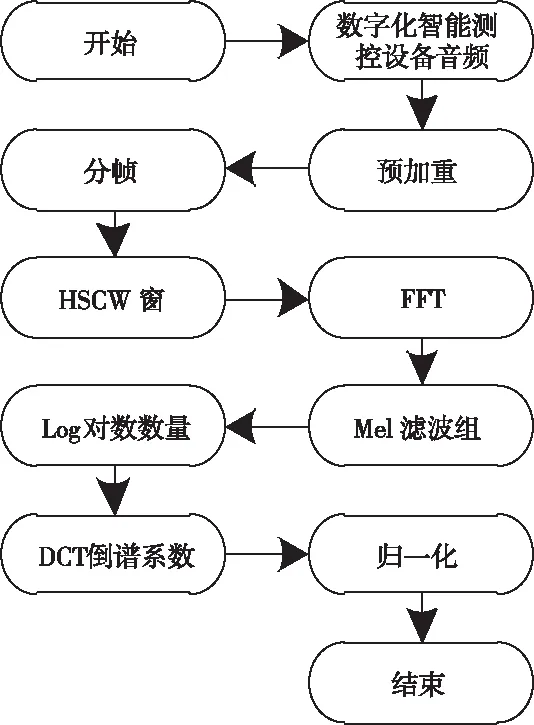
图2 MFCC参数提取流程图
1)预加重
由于声音信号高频信噪比取值较低,借助预加重能够全面增加信号的高频分量和信噪比取值。其中,预加重是通过数字滤波器H(z)实现的,具体的计算式如下
H(z)=1-μz-1
(3)
式中,μ的取值单位在0.93至0.97范围内;z代表信号的高频分量。
2)分帧
将取值单位在10~30ms时间长度的数据点设定为帧长,选取帧长的1/5~3/5作为帧移。
3)加窗
分别对不同的帧数据进行HSCW加窗处理。
4)对经过预处理的音频xi(x)进行快速傅里叶变换,获取音频频谱,信号也由时域转换为频域,对应的计算式为
X(i,k)=FFT[xi(m)]
(4)
式中,X(i,k)代表信号的频域信息。
5)计算能量谱,对应的计算式如下
E(i,k)=FFT[xi(m)]
(5)
式中,E(i,k)代表能量谱。
6)Mel滤波器:
各个三角滤波器对应的传递函数Hm(k)能够表示为
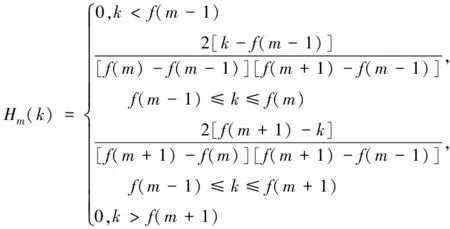
(6)
式中,k代表三角滤波器的总数;f(m)代表数字化智能测控设备对应的信号谱能量,对应的计算式为

(7)
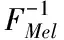
7)计算采用Mel滤波器处理前后的频谱分量。数字化智能测控设备中各帧信号主要利用Mel滤波器获取对应的频谱能量,其中频谱能量是信号频谱能量E(i,k)和Mel三角滤波器频域响应Hm(k)两者的乘积和S(i,m),具体的计算公式为

(8)
8)进行离散余弦变换处理,获取对应的MFCC系数。
9)将全部特征参数进行归一化处理。
在上述分析的基础上,采用人工蜂群算法对SVM中的全部参数进行优化处理[9,10],结合人工蜂群算法的优势,解决全局和局部最优解两者之间存在的矛盾,有效克服SVM进行参数寻优时存在的弊端,更好实现噪声识别。对SVM参数进行优化的目的是:通过ABC算法对SVM的惩罚因子C和核函数参数σ进行选择,确保SVM的识别结果达到最佳。以下给出数字化智能测控设备噪声辨识的具体操作步骤:
1)将全部参数进行初始化处理;
2)形成M个初始坐标解xi;
3)在M个已知坐标附近分别进行搜索,获取对应的目标函数值;
4)将初始坐标解和目标函数值两者进行对比,同时利用贪婪选择算法判定是否需要进行坐标更新;
5)获取已知坐标系在新一轮搜索过程中被选中的几率;
6)通过贪婪选择算法选择局部最优解和对应的坐标值;
7)相同坐标被搜索多次如果依据没有更新,则直接抛弃该坐标,同时采取xij替换坐标,有效实现全局最优搜索;
8)通过计算得到目标函数的最大值和具体坐标值,其中坐标值即为算法的最优解;
9)判断算法是否达到最大收敛次数,如果达到,则输出最优解;反之,则跳转至步骤2)。
2.2 数字化智能测控设备噪声功率自适应控制
为了更好实现噪声功率自适应控制,需要借助噪声功率自适应控制系统完成控制。通过横向结构FIR滤波器进行滤波处理,其中长度设定为M。实际应用过程中,不需要考虑次级源噪声对控制系统产生的影响。
设定r(n)代表滤波-x信号,具体的表达形式为
r(n)=[r(n),r(n-1),…,r(n-M+1)]T
(9)
通过一系列推导能够获取滤波-x递归最小二乘算法的权重矢量更新关系,表示为[11,12]
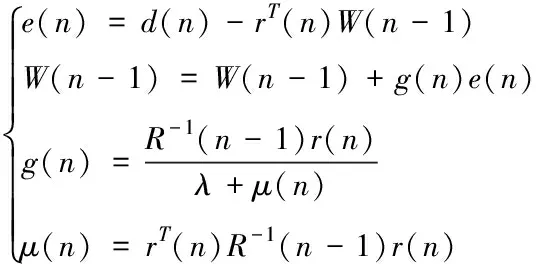
(10)
式中,W(n-1)代表横向滤波器的权重系数;R-1代表联合估计参数;e(n)、g(n)和μ(n)分别代表不同的权重矢量;rT(n)代表预测误差向量的取值范围;λ代表联合估计参数的最优解。
基于QR分解的最小二乘格型自适应滤波器算法是通过多个不同的阶段完成的,具体如下所示:
1)自适应前向预测;
2)自适应后向预测;
3)自适应联合估计。
结合上述分析,能够获取滤波算法对应的有源前馈噪声功率控制系统。进行格型联合估计的主要目的就是根据参考滤波构建级源信号,利用式(11)给出格型的具体预测过程

(11)
式中,fm(n)和bm(n)代表不同类型的次级源信号;kf,m和kb,m分别代表fm(n)和bm(n)对应的前向反馈系数。
其中,控制系统的残余噪声e0(n)能够表示为
e0(n)=d(n)-y(n)·hs(n)
(12)
式中,y(n)代表后向反射系数;hs(n)代表联合估计过程对应的权值系数取值范围。
针对自适应前后向预测过程,需要将采集到的信号全部转换为滤波-x信号r(n)。同时应引用自适应联合估计器对数字化智能测控设备噪声功率自适应控制系统内的全部参数进行自适应修正,得到各个类型信号对应的联合估计回归参数更新式
1)全局误差关系更新式Βm-1(n)为
Βm-1(n)=λΒm-1(n-1)+εb,m-1(n)
(13)
式中,εb,m-1(n)代表各阶残余误差的更新关系。
2)各阶残余误差的更新关系εb,m-1(n)表达式为
εb,m-1(n)=bm-1(n-1)+kb,m(n)-d(n)
(14)
通过上述分析,将滤波器结构和自适应算法相结合,对控制器的内部结构进行有效简化,最终有效控制测控设备噪声功率,详细的操作步骤如下所示:
1)优先对数字化智能测控设备噪声进行辨别,有效识别异常噪声。
2)经过步骤1)操作后,确保在理想状态下,由传递函数、脉冲响应以及系数更新共同组建的通路是完全相等的。
3)将滤波器算法和自适应算法两者进行有效结合,同时确保更新环节中全部关键参数之间的关联。
4)对系统内的输入信号进行初始化处理,将其输入到经过简化处理的控制器中,最终完成数字化智能测控设备噪声自适应控制。
3 仿真研究
为了验证所提数字化智能测控设备噪声功率自适应控制方法的综合有效性,进行仿真测试。
1)噪声功率自适应控制效果分析
优先采集数字化智能测控设备的噪声功率变化情况,将其作为测试对象,分别采用所提方法、文献[3]方法和文献[4]方法进行噪声自适应功率控制,具体的控制结果如图3所示。
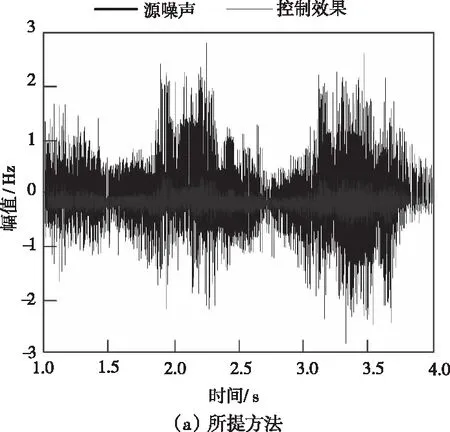

图3 不同方法的噪声功率自适应控制效果对比
分析图3可知,所提方法的噪声功率自适应控制效果明显优于另外两种方法。主要是因为所提方法在实际应用的过程中,针对数字化智能测控设备噪声进行辨识,及时剔除异常噪声,有效为后续的噪声功率控制奠定了坚实的基础,确保控制效果达到最佳状态。
2)音质质量评估
将三种经过噪声功率自适应控制后的语言样本分别输入到感知语音质量评估软件中,分别从噪声残留以及语言失真等多个方面进行评估,获取各组测试语音的客观评分。其中采用百分制评分机制,具体实验结果如表1所示:

表1 不同方法的音质质量评估结果对比
分析表1中的实验数据可知,所提方法能够获取比较满意的音质质量评估结果,评估得分明显高于文献[3]方法和文献[4]方法,充分证明了所提方法的优越性。
3)稳态误差/%
为了更进一步验证所提方法的优越性,以下实验测试对比三种不同方法的稳态误差,具体实验结果如图4所示。
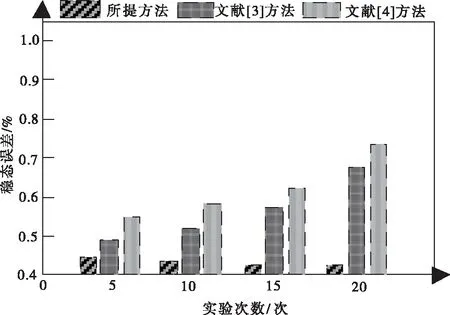
图4 不同方法的稳态误差对比结果
分析图4中的实验数据可知,稳态误差的取值越小,则说明噪声功率自适应控制结果越理想。在三种方法中,所提方法的稳态误差明显更低一些,充分验证了所提方法的优越性,同时更进一步证明了所提方法能够获取更好的控制效果。
4 结束语
针对已有噪声功率自适应控制方法存在的问题,提出一种数字化智能测控设备噪声功率自适应控制方法。测试结果表明,所提方法能够大幅度降低稳态误差,增加音质质量,获取更加理想的噪声功率自适应控制结果。
对于一个完整的噪声功率控制方法而言,不仅需要考虑控制系统的控制性能,同时还需要考虑声源以及声场等相关信息,所以所提方法仍然存在不足,后续将继续对该方法进行改进。

