改进型PSO的6自由度工业机械臂轨迹规划*

师 玮，张金柱，王 涛，李子良，张彦杰，熊晓燕

(太原理工大学a.机械与运载工程学院；b.先进金属复合材料成形技术与装备教育部工程研究中心；c.先进成形与智能装备研究院，太原 030024)

0 引言

随着“中国制造2025”国家实施制造强国战略行动纲领的提出，工业机器人被广泛地应用于工业生产的各个方面，成为我国装备智能制造推进的重点领域。在实现智能化制造生产过程中，机械臂的运用越来越普遍，为了满足高效率生产的需求，对机械臂运动轨迹的设计显得至关重要。

对机械臂的运动轨迹规划主要有基于时间最优、基于能量最优和基于混合最优等3类[1-3]，其中基于时间最优是最常用也是符合生产过程中的基本要求。为了满足智能化生产制造需求，国内外学者对机械臂的轨迹规划进行了深入的研究。柘龙炫等[4]基于RBF神经网络并借助MATLAB中的神经网络工具箱对6自由度机械臂进行了轨迹优化，实验结果降低了趋近误差，表明了轨迹优化的合理性。周晟等[5]针对轨迹运行时间规划问题，提出了一种引入自适应动态旋转角步长调整机制和多算子协同变异机制的改进型量子遗传算法，通过实验研究验证了算法的有效性。郝晗等[6]提出一种基于改进型遗传算法的6自由度机械臂轨迹优化算法并采用三阶B样条多项式轨迹插值规划运动轨迹，通过仿真实验验证该算法的合理性。朱萌等[7]基于R0S仿真平台进行了机械臂运动规划研究，采用RRT和RRTConnect路径规划算法完成路径规划，表明了RRTConnect算法的优越性。赵华东等[8]针对空间6自由度机械臂路径规划问题，提出了一种基于改进蚁群算法大路径规划方法并设计了碰撞检测算法，通过实验验证了该方法的有效性和可行性。张海涛[9]将BP和RBF 神经网络应用于机械臂轨迹规划的逆运动学求解中，通过仿真分析取得了较好的效果。

针对6自由度机械臂在运行中的轨迹规划问题，选取使机械臂能够在最短时间内完成既定运动过程并保证运动轨迹能以光滑平顺的方式到达目标点作为目标函数，提出并设计了一种改进型的粒子群算法(improved particle swarm optimization,IPSO)规划6自由度机械臂的运动轨迹并进行优化，经过实验验证该算法能够有效地减少轨迹运行时间，提高机械臂的实际生产效率，并且保证运动轨迹的平滑性和稳定性。

1 机械臂的运动学分析

1.1 机械臂运动学模型

本文以KUKA KR系列机器人为研究对象，其由底座、转柱、连杆臂、小臂、腕部等部件组成，如图1所示为实验室现有KUKA KR300 R2500 6自由度串联关节式机械臂。

根据D-H模型参数法建立机械臂的各连杆坐标系，如图2所示。该机械臂均为转动关节，末端连接执行机构。由于无论连接底座与转柱之间的转动关节0如何旋转，其长度对整个机械臂的运动均无任何影响，因此令基准坐标系0与坐标系1重合共轴。其余各关节坐标轴方向按照右手定则依次分别确定[10]。

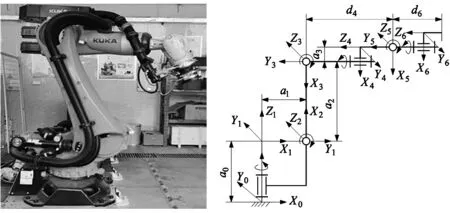
图1 KUKA KR300 R2500机械臂 图2 机械臂坐标系示意图

当工业机器人机械臂坐标系建立好之后，按照给定的机机械臂各连杆参数就可以进行相应的运动学分析计算。各连杆D-H模型参数及相关变量变化范围如表1所示。

表1 KUKA KR300机械臂基本参数

表中，ai-1为连接连杆i-1的相邻两关节轴线的公垂线，即连杆的长度；αi-1为相邻的两个关节之间的夹角，即连杆角；di为ai-1与轴线i的交点到ai与该轴交点的距离，即连杆偏距；θi为ai-1与ai的延长线间的夹角，即相邻两关节之间的角位移。

1.2 机械臂运动学求解

(1)

(2)

变换矩阵的一般表达式为：

(3)

令，si=sinθi；ci=cosθi；sαi=sinαi；cαi=cosαi。

根据坐标变换理论，利用所给参数及连杆变换表达式可得相邻连杆之间的变换矩阵，分别如下：

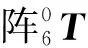
(4)

2 机械臂运动轨迹规划

当前阶段，对机械臂运动轨迹规划设计主要有2种方法：①在关节空间中运用多项式函数插值规划轨迹；②在笛卡尔空间中运用直线(或圆弧)插值结合姿态插值规划轨迹。多项式插值算法作为数值分析的重要方法之一，常被用来对机械臂进行运动轨迹规划。

2.1 多项式插值的构造

为了减少机械臂在运动过程中加速度过大对机械臂的磨损，同时避免多项式阶次过低所求得的加速度为常数的问题，保证其运动过程的平顺性、稳定性，根据实际工况需要，将机械臂的工作区间分为3段，采用3-5-3多项式插值(即：第1、第3段采用三次多项式，第2段采用五次多项式)对机械臂进行轨迹规划设计。实际工作路径可表示为1→2→3→4的三段式，机械臂的起始位置1和终止位置4的速度和加速度均为0，第一段的1→2采用三次插值多项式，第二段的2→3采用五次插值多项式，第三段的3→4采用三次插值多项式。

第i关节3-5-3样条多项式的公式如下：

(5)

用ti(i=1,2,3)表示第i关节的3段插值多项式的时间，多项式的系数aj1i，aj2i，aj3i(j=1,2,…,6)必须满足以下约束条件，即可由上式得到角位移、角速度和角加速度的函数表达式，即：

当0≤t≤t1时，表示为：

(6)

当t1≤t≤t1+t2时，表示为：

(7)

当t1+t2≤t≤t1+t2+t3时，表示为：

(8)

式(5)中所有的系数可以由以上约束求出，系数的关系可表示为：

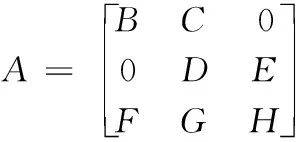
(9)

θ=[0 0 0 0 0 0xj30 0xj00 0xj2xj1]T

(10)

a=A-1θ=[A1A2A3]T

(11)

式中，

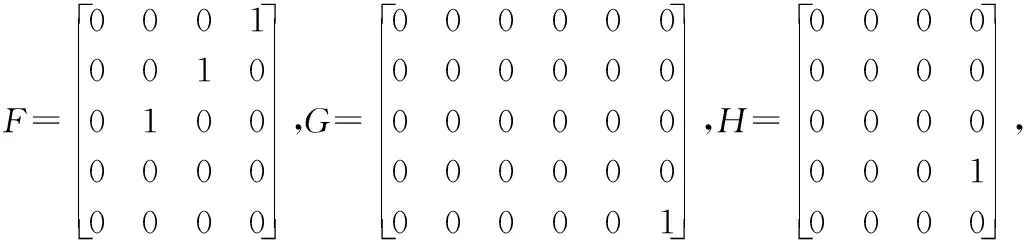
A1=[aj13aj12aj11aj10]，

A2=[aj25aj24aj23aj22aj21aj20]，

A3=[aj33aj32aj31aj30]

2.2 改进的粒子群算法(IPSO)

在传统的PSO中，所有粒子都有一个由被优化函数所决定的适应值，根据粒子们适应度的变化来寻找最优[11-13]。在未找到两个最优解时，粒子可以根据下式来更新自己的速度和位置，即：

(12)

(13)

式中，vid为粒子位置；i为粒子群中的一个任意粒子；d为维度；xid为粒子在相应位置处的速度；ω为惯性权重，即：ω=Wmax-i(Wmax-Wmin)/Nmax；Wmax为最大惯性权重；Wmin为最小惯性权重；Nmax为最大迭代数目；i为迭代次数；c1、c2为学习因子；r1、r2为在[0,1]之间的随机任意值。

轨迹优化的最终目标是在满足运动学约束的条件下，所有关节运动的时间最短。本文引用PSO算法的目的是提高机械臂的实际运行效率，因此以时间最优的适应度函数为：

fitness(t)=min(ti1+ti2+ti3)

(14)

max{|vij|}≤vijmax

(15)

式中，vij为第i个关节的实时速度；vijmax为第i个关节的最大限制速度。

标准的PSO算法运算简单、效率高且搜索的速率快，但是易陷入局部最优解，况且其中的权重因子是固定值[14-16]。为了解决上述问题，本文提出并采用动态变化的权重因子来获取更高的收敛效率，使得最优解更优化，因此，可采用以下公式确定学习因子，即：

(16)

(17)

全局学习因子会随着搜索次数的增加而不断地减小，局部学习因子会随着搜索次数的增加而不断地增加[17-19]。通过采用动态变化学习因子的方式可使得在搜索的前期能够快速到达全局最优，后期快速到达局部最优，这样既可以提高搜索效率，又能优化结果出现局部最优解的不足[20-21]。改进的粒子群算法(IPSO)求解机械臂关节运动最优时间的流程图如图3所示。本文所采用动态变化学习因子策略的改进型粒子群算法，以时间为适应度函数对运动轨迹进行优化，将分段高次多项式插值函数与传统PSO算法有效结合，实现机械臂运动时间的最优求解。相较于前人的改进和研究，本文所采用方法的收敛速度更快，运行效率更高，运动特性更好。

图3 改进的粒子群优化算法流程图

3 仿真与分析

3.1 仿真设计

为验证本文所提出的一种基于改进后PSO算法的3-5-3插值多项式对机械臂进行轨迹规划设计的可行性和优劣性，本文以KUKA KR300 R2500机械臂为研究对象，使用MATLAB中的仿真工具箱进行了仿真实验研究。借助MATLAB工具箱中的Link函数，搭建6自由度串联机械臂轨迹规划平台，控制界面如图4所示。依据所搭建的平台来验证机械臂正、逆运动学求解正确性，保证运动规划的有效性、合理性和可行性，实现对6自由度机械臂运动轨迹的优化设计。

图4 机械臂轨迹规划平台

为了更加准确地获取机械臂末端执行器的笛卡尔空间坐标信息，对机械臂正运动学进行求解，得到机械臂的起始点空间坐标位置和终止点空间坐标位置。运用MATLAB中的机器人工具箱求出另外的两个中间插值点，最终可以获得机械臂运动轨迹规划的所有插值点。区间划分及插值点位置坐标如表2所示。

表2 机械臂末端执行器轨迹位置坐标

通过运用MATLAB对机械臂的逆运动学进行求解，可以得到4个插值点所对应的关节角度值。各插值点对应关节角度如表3所示。

表3 各插值点对应关节角度

3.2 实验验证与结果分析

在进行机械臂轨迹规划时，应用3-5-3多项式插值方法结合改进后的PSO算法，可以得到前3个关节的插值结果。本文选取随机初始粒子数m=20，最大迭代次数Nmax=100，通过Nmax次迭代不断更新粒子，计算出添加了约束条件后的最优解粒子，该粒子即为所需的最优时间粒子。

6自由度串联机械臂满足机器人学中的Pieper准则，即3个腕关节(关节4、5、6)的轴相交于一点。这些腕关节的运动只改变末端执行器的姿态，而不改变其位置，所以以机械臂前3关节为主要研究对象得出经IPSO优化后的结果，将经PSO后的时间解同IPSO优化后的结果进行比较。

关节1、2、3分别经传统PSO算法和改进PSO算法优化后的时间收敛图如图5～图7所示。可以看出，采用动态变化学习因子的方式可使得在搜索前期粒子群体能够在较短的时间内搜索到最优粒子快速到达全局最优，同时也能有效保证在后期的搜索过程中能快速准确的收敛到最优解快速到达局部最优。

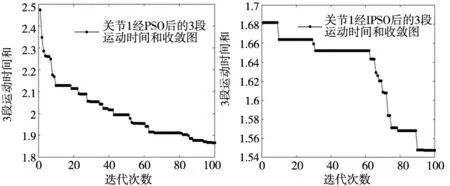
(a) 关节1传统PSO时间收敛图 (b) 关节1改进PSO优化后时间收敛图

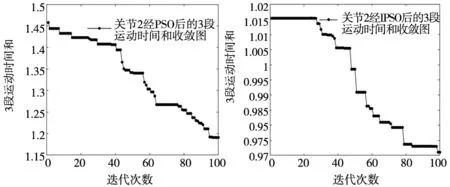
(a) 关节2传统PSO时间收敛图 (b) 关节2改进PSO优化后时间收敛图

(a) 关节3传统PSO时间收敛图 (b) 关节3改进PSO优化后时间收敛图

从表4中可以看出，传统PSO算法的所需时间为3.5 s左右，改进后的PSO算法所需时间为1.7 s左右。二者相比，轨迹运动所需时间缩短了约50%左右，可以满足预期要求，仿真实验验证了本文所提改进型粒子群算法串联关节机械臂运动轨迹规划时间优化问题中的可行性。使用IPSO既可以提高搜索效率，又能优化结果出现局部最优解的不足，获取更好的运动特性。

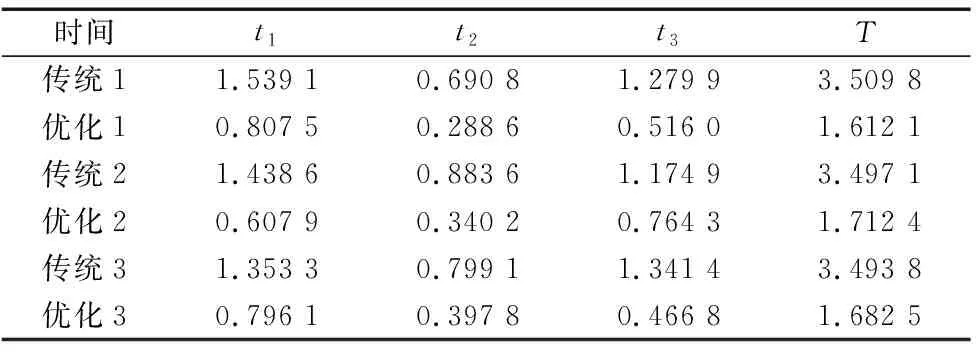
表4 优化前后结果

4 结论

针对6自由度工业机械臂的运动轨迹优化问题，提出了一种时间最优的基于改进型粒子群算法的6自由度串联式机械臂运动轨迹优化方法。采用动态变化学习因子策略的改进型粒子群算法进行3-5-3高次多项式插值，来完成机械臂的运动轨迹拟合。通过仿真实验验证分析可知，该方法不仅能使得机械臂在工作过程中的加速度不会产生突变，还可获得较高的运动轨迹精度，使机械臂工作时间达到最优。本文提出的算法相比于其他运动轨迹规划算法更易于实现，可在提高运行效率的同时保证整体运行的平稳性和光滑性。该方法的可行性能为今后机械臂的运动轨迹优化问题提供一定的理论依据。