数控机床直线轴定位误差建模与补偿

陈齐林，吴 晗，姚振强，邓鹏宇

(1.上海交通大学机械与动力工程学院，上海 200240；2.上海交大智邦科技有限公司，上海 200120)

0 引言

数控机床是现代制造业生产加工的基础，其加工精度的好坏直接决定了被加工件的质量[1]。根据产生误差的不同机理，数控机床的加工误差主要分为4种：几何误差、热误差、力误差以及控制误差[2]。其中几何误差是在机床设计制造以及装配过程中引入的误差，是数控机床最重要的误差来源[3]，而定位误差又是几何误差中重要的组成部分。因此，减小定位误差对机床加工精度的提升十分重要。

数控机床定位误差的检测方法较为成熟，可以分为直接测量法和间接测量法[4]。测量仪器有球杆仪、平面光栅、R-Test、激光干涉仪和激光跟踪仪等，其中激光干涉仪具有测量精度高、范围大等优点，被广泛应用于机床精度检测[2]。国内外学者提出了多种激光干涉仪测量数控机床定位误差的方法，如22线法[5]、15线法[6]等。同时国内外学者对机床定位误差建模也做了大量研究。WANG等[7]使用牛顿插值法对立式加工中心的定位误差进行建模。李自汉[8]提出了一种基于移动最小二乘法与Chebyshev多项式相结合的定位误差建模方法。FAN等[9]通过基于最小二乘法的正交多项式对定位误差进行拟合，通过对一般多项式基函数进行正交化处理，有效地提高了建模的精度。

以上研究都是基于激光干涉仪测量结果对机床定位误差进行分析建模，但由于测量过程中激光干涉仪和光栅尺不共线，会在测量结果中引入阿贝误差[10]，影响建模准确性和补偿精度。王超[11]通过实验验证了阿贝误差对不同测量点定位误差的影响。LIU等[12]设计了一种测量方法避免在测量过程中引入阿贝误差。上述研究成果主要是通过理论验证阿贝误差，并未对直线轴运动行程内的定位误差进行建模分析。本文通过分析不同测量高度下的定位误差，将定位误差分离为基准定位误差和阿贝误差，采用多项式拟合和线性拟合建立了直线轴定位误差综合模型，通过综合模型得到的结果对机床进行误差补偿，大幅度提升了机床的加工精度。

1 定位误差测量

1.1 测量系统与方案

测量对象为某型号数控磨床，使用雷尼绍XL-80干涉仪对X轴(砂轮架)的定位误差进行测量，如图1所示。

实验采用ISO230-2标准推荐的双向线性循环测量[13]，如图2所示。具体测量过程为：在直线轴行程范围内均匀设置一系列测点，当数控机床按照指令到达某一被测点坐标位置时停止运动，此时激光干涉仪测量并记录下该测点的位置信息，随后数控机床运行到下一测点进行测量，直至正向测量完毕，直线轴在越程后开始反向运动并进行测量，直至返回到最初的起点，以上称为一个测量循环。对于两米以内的直线轴，ISO标准推荐每米不少于5个测点，循环次数为5次。

图1 定位误差测量系统 图2 双向线性循环测量模式

一般情况下，同一直线轴测点数目越多，越能够准确反映其定位精度，但测量时间也会越久，测量过程中引入的随机误差也就越多。数控机床X轴有效工作行程为150 mm，需要确定合适的测点数目，以便在准确反映其定位误差的同时控制时间成本为最小。为此固定循环次数为5次，测点数目从3个逐渐增加到17个，测量结果如图3所示。从图中可以看出，测点数目为3个时，定位误差测量结果最小，随着测点数目逐渐增多，定位误差测量结果先变大后逐渐稳定下来。最佳测点数目为11个，此时能够准确反映X轴定位精度，且测量时间较短，因此后续测量选用11个测点。

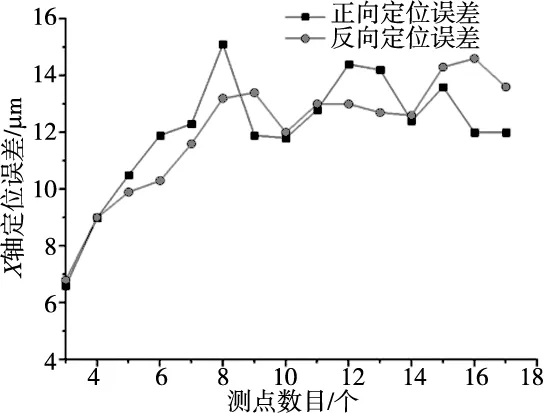
图3 测出的定位误差与测点数目的关系

1.2 测量结果与分析

1.2.1 不同预热时间定位误差测量

在精密机床中，温度对机床的定位误差有很大的影响，热误差最高可占总误差的40%[3]。机床刚开机的状态为冷机状态，加工前需要使运动轴在行程范围内高速往复运动进行预热。为了判断机床达到热平衡所需要的预热时间，将机床预热90 min，预热过程中每间隔10 min测量一次定位误差，测量结果如图4所示。可以看出，不同预热时间下X轴的定位误差曲线形状相似，但随着机床预热时间的增加，定位误差曲线斜率逐渐变大，尾部有上翘趋势。而且，在预热的初始阶段曲线斜率变大速度最快，随着预热时间的增加曲线斜率变化速度逐渐减小，预热90 min时，定位误差曲线基本稳定下来，此时机床达到热平衡状态。

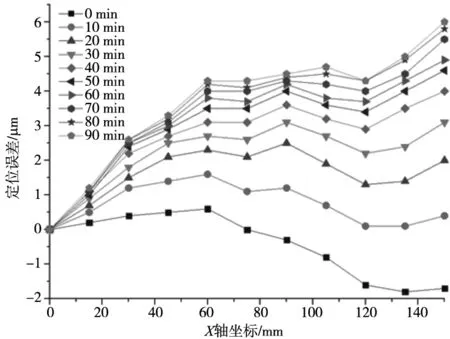
图4 不同预热时间下的定位误差

1.2.2 不同镜组高度下定位误差测量

对直线轴定位误差进行测量时，激光干涉仪一般安装在工作台面，随工作台一起运动，由于激光干涉仪和光栅尺不共线，会在测量过程中引入阿贝误差[10]，如图5所示。

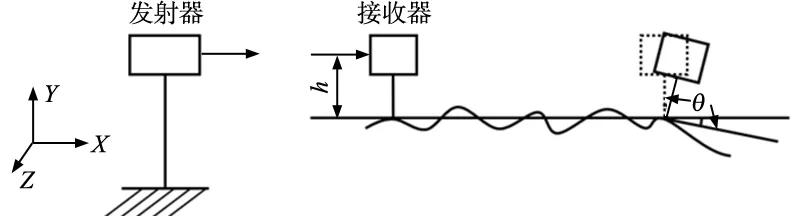
图5 测量过程中引入的阿贝误差

当激光干涉仪镜组与光栅尺距离为h时，若此时工作台面与水平面有一夹角θ(x)(即俯仰角)，则引入的阿贝误差为：

δh(x)=-htanθ(x)≈-hθ(x)

(1)

从式(1)可以看出阿贝误差与高度h成正比，对于同一根直线轴，如果两次测量中激光干涉仪镜组高度不同，测出的定位误差也会有差异，因此有必要对激光干涉仪在不同镜组高度下测量的定位误差进行分析。

如图6所示，激光干涉仪镜组分别安装在距离工作台竖直高度为130 mm、210 mm、290 mm时对X轴定位误差进行测量。为了避免热误差影响，在每次调整镜组高度后均进行90 min热机再进行测量。

具体测量过程如下：

步骤1：机床开机，在高度为h1=130 mm位置安装并调试激光干涉仪；

步骤2：X轴高速运行90 min，机床达到热平衡状态；

步骤3：测量X轴0～150 mm行程内定位误差；

步骤4：在高度为h2=210 mm位置安装并调试激光干涉仪，重复步骤2和步骤3；

步骤5：在高度为h3=290 mm位置安装并调试激光干涉仪，重复步骤2和步骤3。

测量结果如图7所示。可以看出，由于阿贝误差的影响，随着镜组高度的变高，测得的X轴的定位误差有一定程度的变大，与上文所分析的结果一致。

图6 不同镜组高度 图7 不同镜组高度下定位误差

2 定位误差建模与补偿

2.1 定位误差建模

由前文的分析可知，测得的X轴定位误差δ(x)由两部分叠加组成：

δ(x)=δg(x)+δh(x)

(2)

式中，δ(x)是固定不变的基准定位误差，这部分误差是X轴本身的几何误差，主要是导轨制造装配过程产生的；δh(x)是不同镜组高度导致的阿贝误差，由式(1)可知，这部分误差在数值上等于激光干涉仪镜组与光栅尺的距离和工作台俯仰角的乘积。

2.1.1 基准定位误差建模

将高度h1=130 mm定义为参考高度，在此高度测得的误差定义为基准定位误差。用不同阶次多项式分别拟合基准定位误差，表1列出了不同阶次拟合精度对比。

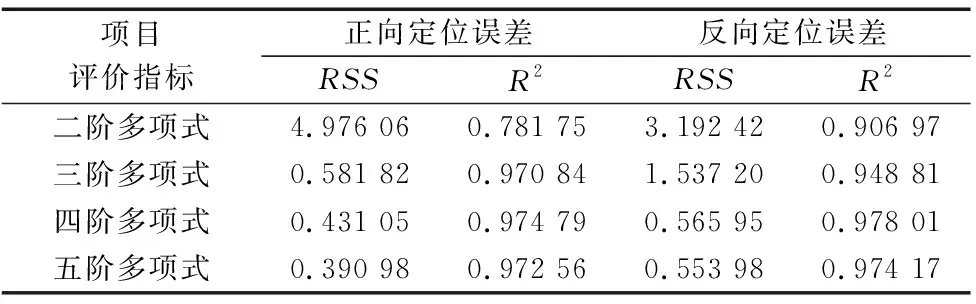
表1 不同阶次多项式拟合精度对比

可以看出，随着多项式拟合阶次的变大，拟合结果的精度越好，当达到四阶时，拟合精度已经达到较高水平。因此基准定位误差选用四阶多项式进行拟合，正反向基准定位误差拟合结果如式(3)和式(4)所示。

δg(x)↑=0.431+0.13655x-9.66805×10-4x2-
3.43607×10-6x3+3.77949×10-8x4

(3)

δg(x)↓=-0.05175+0.07158x+0.00125x2-
2.39278×10-5x3+9.5926×10-8x4

(4)

式中，x为X轴坐标位置；上箭头代表正向；下箭头代表反向。

2.1.2 阿贝误差建模

将在高度h2=210 mm和h3=290 mm下测得的定位误差分别减去高度h1=130 mm下测得的基准定位误差，并将所得值相加，相加结果为相对于基准高度累计240 mm高度差下的阿贝误差值。则单位高度差下的阿贝误差值为：

(5)

图8中的散点是计算出的单位高度差下的阿贝误差值，可以看出其有明显的线性关系，故对计算得到的结果进行线性拟合，拟合直线如图8所示。

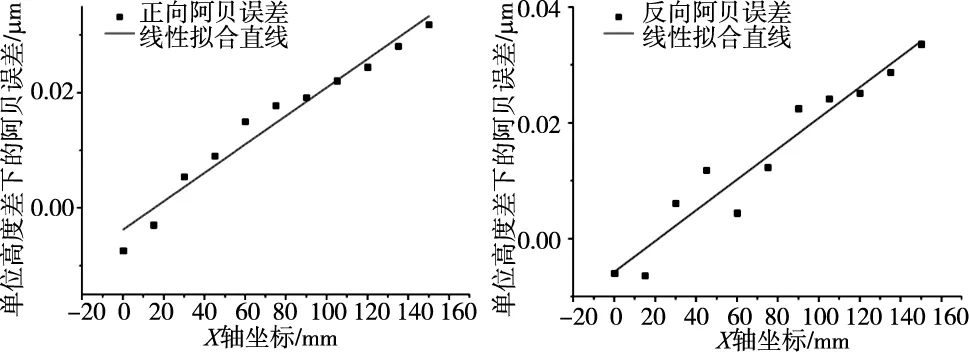
(a) 单位高度差下的正向阿贝误差 (b) 单位高度差下的反向阿贝误差

阿贝误差拟合结果如式(6)和式(7)所示。

δh(x)↑=(-0.00373+0.000246x)h

(6)

δh(x)↓=(-0.00569+0.000265x)h

(7)

式中，x为X轴坐标位置；h为激光干涉仪相对于参考高度的高度差；上箭头代表正向；下箭头代表反向。

2.1.3 定位误差综合建模

由式(2)可知，基准定位误差与阿贝误差之和即为定位误差的综合模型：

δ(x)↑=δg(x)↑+δh(x)↑=0.431+0.13655x-

9.66805×10-4x2-3.43607×10-6x3+3.77949×

10-8x4+(-0.00373+0.000246x)h

(8)

δ(x)↓=δg(x)↓+δh(x)↓=-0.05175+0.07158x+

0.00125x2-2.39278×10-5x3+9.5926×

10-8x4+(-0.00569+0.000265x)h

(9)

定位误差综合模型的拟合结果如图9所示。

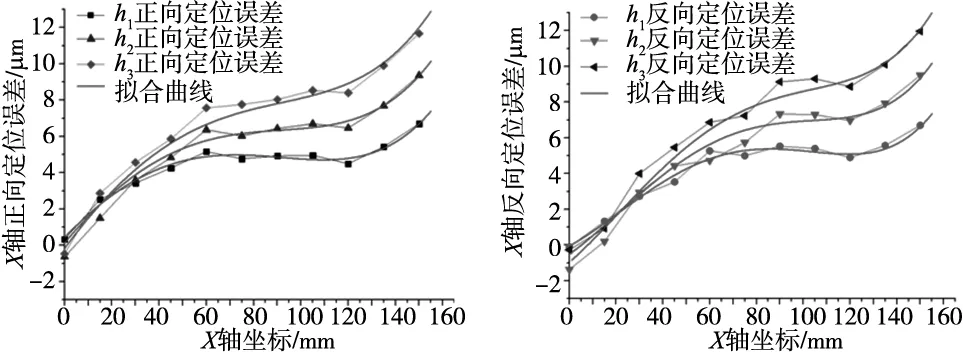
(a) 正向定位误差拟合结果 (b) 反向定位误差拟合结果

将3个不同高度下正反向定位误差共66个点的拟合残差汇总，如图10所示。可以看出综合模型拟合结果整体残差在[-1 μm,1 μm]范围内，拟合结果较好，能够准确反映不同高度下X轴的定位误差。

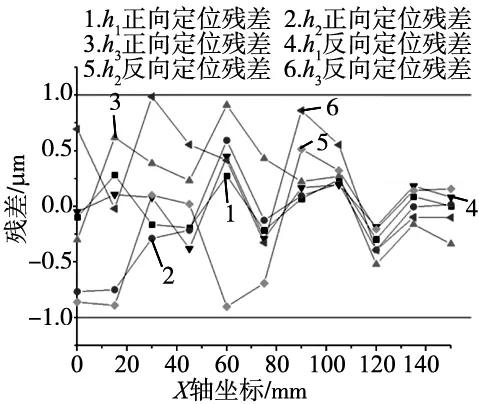
图10 综合模型拟合残差

2.2 定位误差补偿

误差补偿是相对于误差防止提出的，是指人为产生一种与原始误差大小相等方向相反的新误差以抵消原始误差。通过上文得出的定位误差综合模型计算出定位误差值，再将补偿信号输入西门子840D数控系统。补偿前后X轴正反向定位误差曲线如图11所示。

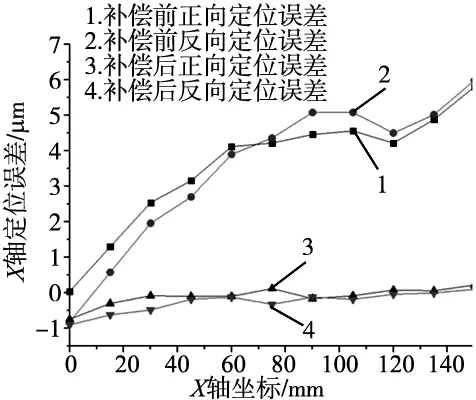
图11 补偿前后定位误差

表2是根据ISO230-2标准计算出的补偿前后双向定位误差[13]，可以看出通过误差补偿，正向定位误差从原来的6.3 μm降低到2.4 μm，误差减小了61.9%；反向定位误差从原来的7.6 μm降低到2.3 μm，误差减小了70%。通过误差补偿，机床X轴的定位精度得到了大幅提升。

表2 补偿前后定位误差 (μm)

3 结论

实验表明，使用激光干涉仪测量数控机床的直线轴定位精度时，随着激光干涉仪镜组高度的增加测得的定位误差有一定程度增大。通过分析不同镜组高度下的定位误差，将定位误差分离为基准定位误差和阿贝误差两个组成部分，分别进行多项式拟合和线性拟合，得到了定位误差综合模型。使用综合模型对机床定位误差进行补偿，结果显示机床精度得到了大幅提升，验证了模型的正确性。