双机器人系统运动学建模与仿真*

武永强，于 涛，纪 俐

(1.辽宁工业大学机械工程与自动化学院，锦州 121001；2.沈阳航空航天大学机电工程学院，沈阳 110000)

0 引言

目前，双机器人协调作业被越来越多的企业应用。双机器人协调作业的研究和开发已成为机器人研究领域中重要且具有活力的一个分支[1]。

单个机器人运动学建模已经十分成熟，运动学模型均根据D-H参数法来建立。曹启贺等[2]用齐次坐标变换推出理论上的坐标变换方程，结合D-H参数法，创建KUKA-KR16机器人的结构模型；赵文强、郝建豹等[3-4]用D-H参数法建立机械臂运动学模型，分析其正、逆运动学问题；上述均用MATLAB验证建立的模型是否正确，建立的模型没有与真实的机器人进行比对。本文将用改进D-H参数法建立ABB-IRB120型机器人的运动学模型并且与实际机器人进行比对，验证运动学建模的正确性。

双机器人系统也不乏有学者研究，于广东等[5]将双机器人协调分为两类，分析了其运动学关系；史帅刚、杨国等[6-7]从主从机器人不同的末端位姿约束关系出发，分析了主从机器人运动学关系。本文将在单个机器人运动学建模的基础上，提出基于标定模型的基坐标系标定方法进行双机器人基坐标系标定，进而推出双机器人运动学模型。

1 单机器人建模与验证

1.1 机器人坐标系

根据文献[8-9]，建立ABB-IRB120型机器人D-H坐标系如图1所示。进一步得到ABB-IRB120型机器人的改进D-H参数[10]如表1所示。

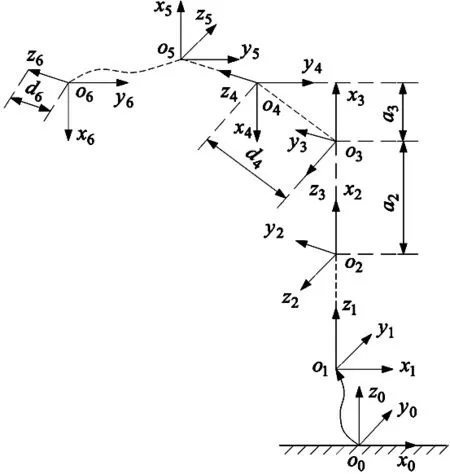
图1 ABB-IRB120型机器人D-H坐标系

表1 ABB-IRB120型机器人的改进D-H参数

表1中，θi表示第i关节的关节转角；di表示第i连杆的关节距离；ai-1表示第i-1连杆的连杆长度；αi-1表示第i-1连杆的连杆扭角；βi表示第i关节的关节角偏移量；α1=90；α3=-90；α4=90；α5=90；a2=270；a3=70；d4=302；d6=72；β2=90；β5=-180；θ1=(-165°～165°)；θ2=(-110°～110°)；θ3=(-90°～70°)；θ4=(-160°～160°)；θ5=(-120°～120°)；θ6=(-400°～400°)。

由于机器人的0关节角位姿状态往往是不规则的位形，为了使其变为一些更为明显的位形，表1中引入关节角偏移量β。

1.2 正运动学

使用改进的D-H算法[11]建立机器人的运动学模型，坐标系{Oi-1}到坐标系{Oi}之间的坐标变换，可由式(1)得到：

(1)

将表1中的参数代入式(1)，可得各连杆的变换矩阵如下：

式中，Ti表示连杆坐标系i相对于连杆坐标系i-1的变换矩阵；i=1,2,3,4,5,6。

上述变换认为机器人的基坐标原点位于机器人内部结构的腰关节和肩关节轴线的交点上。ABB-IRB120型机器人有一个290 mm的底座结构，需要通过坐标变换将机器人基坐标系的原点转移到机器人底座的下端面的中心[15]。该变换矩阵为：

将基坐标系的变换矩阵和各连杆的变换矩阵依次相乘，得机器人正运动学方程[12-14]：

(2)

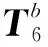
nx=c6(c5(s1s4-c4c1c23))+s5c1s23-s6(c4s1+s4c1c23)

ny=s6(c1c4-s4s1c23)-c6(c5(c1s4+c4s1c23)-s5s1s23)

nz=s6(c1c4-s4s1c23)-c6(c5(c1s4+c4s1c23)-s5s1s23)

ox=-c6(c4s1+s4c1c23)-s6(c5(s1s4-c4c1c23)+s5c1s23)

oz=-s5(c1s4+c4s1c23)-c5s1s23

ax=s5(s1s4-c4c1c23)-c5c1s23

ay=-s5(c1s4+c4s1c23)-c5s1s23

az=c4s5s23-c5c23

px=d6(s5(s1s4-c4c1c23)-c5c1s23)-a3c1c23+d4c1s23-a2c1c2

py=-a3s1c23+d4s1s23-d6(s5(c1s4+c4s1c23)+

c5s1s23)-a2c2s1

pz=a3s23+d4c23-d6(c5c23-c4s5s23)+a2s2+290

式中，s1=sinθ1；c1=cosθ1；s23=sin(θ2+θ3)；c23=cos(θ2+θ3)，以此类推，后文相同。

1.3 逆运动学

(1)求解θ1、θ2、θ3。根据位姿分离的方法，连杆坐标系的{4}、{5}、{6}坐标系的坐标原点相对于基坐标系的位置是相同的，所以利用连杆{4}坐标系的坐标原点即机器人末端的坐标原点[16]。

由变换矩阵T4易得坐标系{4}的坐标原点在坐标系{3}中的表述为：

3p4=[a3-d4sα3d4cα31]T

(3)

结合式(2)，进而可得机器人末端在基坐标系下的表述为：

(4)

(5)

将T0、T1、T2、T3和式(3)代入式(5)并展开，令等式左右两边矩阵(2,1)元素相等，可得：

pxs1-pyc1=0

(6)

根据式(6)，进一步可得：

θ1=arctan2(py,px)

或者

θ1=arctan2(-py,-px)

(7)

将T0、T1、T2和T3以及式(3)代入式(7)并展开，令等式左右两边的矩阵中的元素(1,1)和元素(2,1)分别对应相等，可得：

As2-Bc2=C

(8)

Ac2+Bs2=D

(9)

式中，A、B、C、D分别为：

A=pz-290

B=pxc1+pys1

C=a2+a3c3-d4s3

(10)

D=d4c3+a3s3

(11)

A2+B2=C2+D2

(12)

将式(10)、式(11)带入式(12)得：

a3c3-d4s3=k

(13)

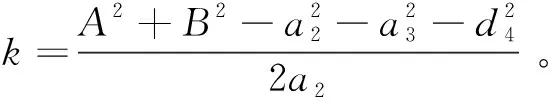
利用三角代换可以解得：

解得以后，代入式(10)和式(11)，得到C和D的值。最后，将式(9)利用三角代换，得：

至此，θ1、θ2、θ3求解完毕。

(2)求解θ4、θ5、θ6。求解θ4、θ5、θ6必须依据姿态矩阵来建立有效的方程求解，上述已经求得θ1、θ2、θ3，后面将T1、T2、T3视为已知量。根据式(2)可以得到：

(14)

基于遥感的岸线变迁及其在电力工程的应用……………………………………胡进宝，刘海成，王晓霞，等（3.89）

(15)

式(15)中等式两边的矩阵元素(2,3)相等，得：

c5= -azc23-s23(axc1+ays1)

(16)

式(16)进一步变形可得：

式(15)中，根据等式左右两边的矩阵中的元素(1,3)、(3,3)、(2,1)、(2,2)分别对应相等，可得以下两组方程：

(17)

(18)

根据式(17)、式(18)可得：

当s5>0时，

θ4=arctan2(axs1-ayc1,azs23-(axc1+ays1)c23)

θ6=arctan2(-ozc23-(oxc1+oys1)s23,nzc23+(nxc1+nys1)s23)

当s5<0时，

θ4=arctan2(ayc1-axs1,(axc1+ays1)c23-azs23)

θ6=arctan2(ozc23+(oxc1+oys1)s23,-nzc23-(nxc1+nys1)s23)

至此，θ4、θ5、θ6求解完毕。

1.4 机器人模型的验证

(1)模型建立。根据表1所示的ABB-IRB120型机器人的D-H参数，使用MATLAB中的Robotics Toolbox建立机器人运动学模型[17]，得到IRB120机器人模型如图2所示。

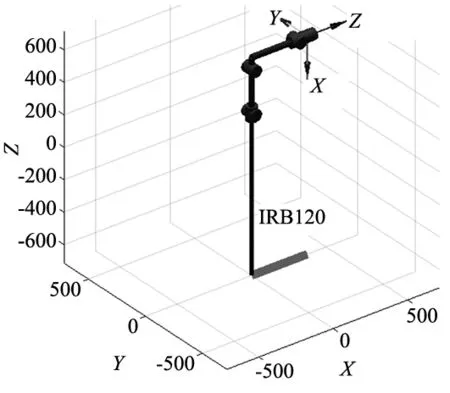
图2 IRB120机器人运动学模型

使用命令：IRB120_R1.fkine([0 0 0 0 0 0])，在命令框中可以得到如图3所示的位姿矩阵。

>>IRB120_R1.fkine([0 0 0 0 0 0])ans=-0.0000-0.00001.0000374.00000.00001.00000.00000.0000-1.00000.0000-0.0000630.00000001.0000

(2)实物验证。在RobotStudio中建立ABB-IRB120机器人系统，使各个关节角度归零，通过机器人示教器手动操作界面可以看到机器人末端(不含工具)相对于机器人基坐标系的位移以及欧拉角如图4所示。

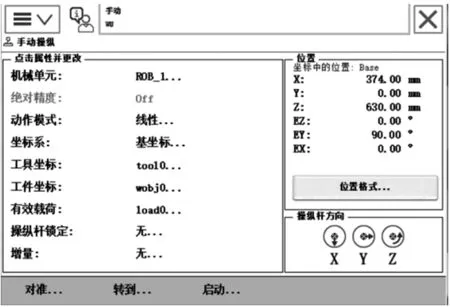
图4 ABB-IRB120工业机器人关于基坐标的末端位姿

为了方便和图4比较，图3的位姿矩阵拆分为位置矩阵和姿态矩阵。

位置矩阵为：

P=[374,0,630]T

姿态矩阵为：

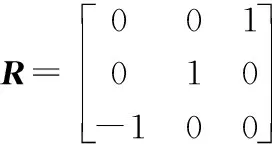
图4示教器中的位置矩阵：

P′=[374,0,630]T

姿态是用欧拉角表示的，将其转换为相对于基坐标系的位姿矩阵形式，变化如下：

R′={b}RY(90°)

(19)

式中，{b}表示机器人的基坐标系：

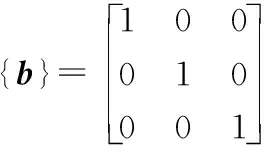
(20)

RY(θ)表示绕Y轴旋转θ角度的正交旋转矩阵：

(21)

结合式(19)、式(20)和式(21)，可以得到图4示教器中的姿态矩阵：

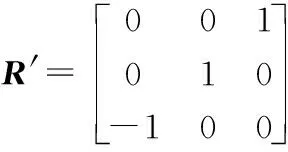
机器人模型得到的位置矩阵P和姿态矩阵R与仿真得到的位置矩阵P′和姿态矩阵R′进行比较，发现：

P=P′
R=R′

显然，使用MATLAB建立的模型和实际机器人完全一致，所以该模型建立是正确的。

2 双机器人系统运动学建模

2.1 双机器人系统基坐标系标定

(1)坐标系的建立及标定原理。如图5标定原理图所示，主从机器人基坐标分别为{O1}和{O2}。

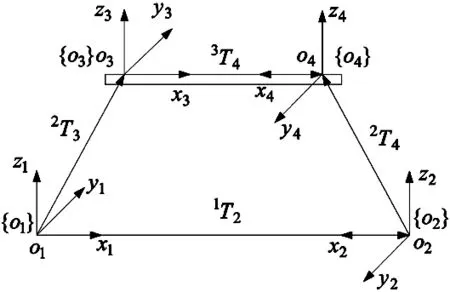
图5 标定原理图

双机器人基坐标系的标定目的在于确定坐标系2相对于坐标系1之间的变换矩阵。通过图5所示的标定原理图可得：

1T2=1T3·3T4·(2T4)-1

(22)

(2)具体标定。首先，示教机器人R1，使标定针针尖接触标定模型上的坐标系1的坐标原点，记该点为p11，记录此时机器人R1各关节的角位移(记为ψ11)以及p11在基坐标系下的坐标值；然后，继续示教机器人R1，使其接触标定模型上的坐标系3的X轴和Y轴上任意一点，分别记点p12和p13，同样记录在p12和p13点时机器人1各关节的角位移(分别记为ψ12和ψ13)以及在基坐标系下的坐标值；最后，可以得到以下数据：

p11=(x11y11z11)
p12=(x12y12z12)
p13=(x13y13z13)
ψ11=(φ111φ112φ113φ114φ115φ116)
ψ12=(φ121φ122φ123φ124φ125φ126)
ψ13=(φ131φ132φ133φ134φ135φ136)

式中，ψij为第pij点机器人i的关节角度；φijm为第pij点机器人i的m关节的角位移。

同理，使用相同的方法，示教机器人R2标定针接触标定模型上的坐标系4，得到以下参数：

p21=(x21y21z21)
p22=(x22y22z22)
p23=(x23y23z23
ψ21=(φ211φ212φ213φ214φ215φ216)
ψ22=(φ221φ222φ223φ224φ225φ226)
ψ23=(φ231φ232φ233φ234φ235φ236)

由于p11、p12、p13是标定模型上的坐标系3上取的三点，利用三点建立一个坐标系：以p11点为坐标原点，以p11p12方向为X轴方向，以p11p13方向为Y轴方向，Z轴方向通过X轴方向的方向向量和Y轴方向的方向向量差乘运算获得，如此便完成了图5标定原理图中的坐标系3的构建。

同理，用相同的办法，完成坐标系4的构建。

根据上述坐标系3的构建方法，取：

(23)

(24)

式中，u和v分别为坐标系3的X轴和Y轴的方向向量，则Z轴的方向向量为：

w1=u1×v

(25)

得到坐标系3相对于坐标系1 的变换矩阵：

(26)

同理，坐标系4相对于坐标系2的变换矩阵为：

(27)

标定模型上的坐标系3和坐标系4的坐标变换3T4是已知的，将式(26)、式(27)以及3T4代入式(22)便可确定机器人R2的基坐标系相对于机器人R1的基坐标系的变换矩阵为：

(28)

至此双机器人系统的基坐标系标定任务完成。

2.2 双机器人系统运动学模型

如图6所示，R1和R2分别为主、从机器人；{O1}为R1的基坐标系；{O2}为R2的基坐标系；{O}为世界坐标系。

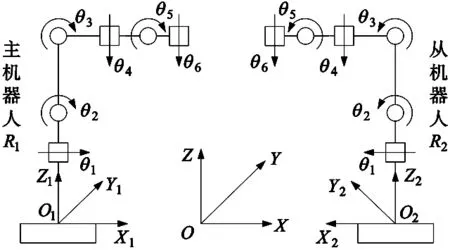
图6 主从机器人运动学模型简图

已知主从机器人基坐标系之间的位姿关系1T2，主(从)机器人末端坐标系相对于主(从)机器人基坐标系之间的位姿关系TR1(TR2)。若以主机器人的基坐标系作为双机器人系统的基坐标系，主从机器人末端到达空间中的某一位置，则从机器人的运动学方程为：

TR2=(1T2)-1·TR1

(29)

若主从机器人的末端没有到达同一位置，则有：

R1TE2=1T2·TR2

(30)

式中，E2为从机器人的末端坐标；R1TE2为从机器人末端坐标系相对于主机器人基坐标系的位姿变换。

同理，可得从机器人R2的基坐标系和主机器人末端坐标系之间的关系为：

R2TE1=(1T2)-1·TR1

(31)

3 仿真验证

3.1 基坐标系标定理论验证

在理想状态下，如图7所示，假设主从机器人同平面相对而立，在X轴方向相距800 mm。

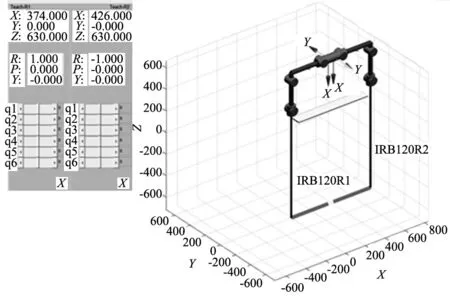
图7 双机器人标定系统

主从机器人基坐标系之间的位姿变换矩阵为：

(32)

姿态矩阵R′为：

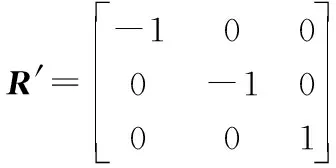
(33)

位置矩阵T′为：

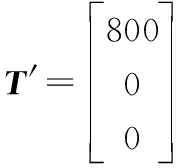
(34)

标定模型上坐标系4相对于坐标系3的变换矩阵为：

(35)

在MATLAB的机器人工具箱中建立如图9所示的双机器人标定系统，然后按照本文提出的标定法方进行标定，得到的数据如表2所示。

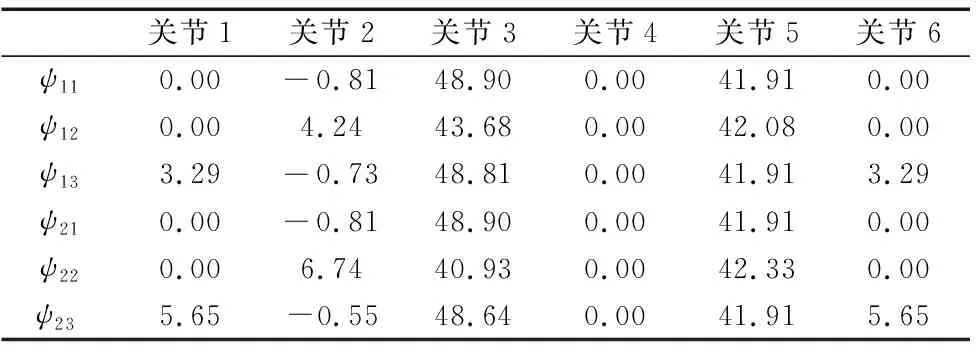
表2 机器人R1和R2在3个接触点的各关节角度 (°)

表2中的数据代入式(23)～式(27)，得到坐标系3相对于坐标系1的变换矩阵为：

(36)

坐标系4相对于坐标系2的变换矩阵为：

(37)

结合式(28)、式(35)～式(37)，最终可以得到机器人R2的基坐标系相对于主机器人R1的基坐标系变换矩阵为：

(38)

3.2 运动学模型理论验证

假设主从机器人同平面相对而立，在X轴方向相距800 mm，如图8所示。

图8 双机器人系统模型

图8可知，主机器人R1的基坐标系的坐标原点和双机器人系统的世界坐标系的原点重合，主从机器人基坐标系之间的位姿变换矩阵和式(32)相同：

(39)

从机器人R2的末端坐标系相对于主机器人R1的基坐标系的位姿变换为：

(40)

根据式(2)从机器人的运动学方程得到从机器人末端坐标系和基坐标系之间的位姿关系为：

(41)

由于主从机器人的末端没重合，故将式(39)和式(40)带入式(30)，得从机器人R2的末端坐标系相对于主机器人R1的基坐标系的位姿变换为：

(42)

对比式(40)和式(42)，可见该模型理论上是正确的。

3.3 运动学模型仿真验证

如图9所示，建立双机器人系统工作站。为方便主从机器人在空间中的某一点精准“握手”，主从机器人均加上相同的标定针。

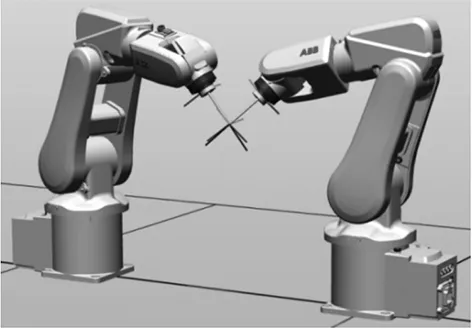
图9 双机器人系统工作站

主从机器人的标定针末端到达空间中的同一位置，从示教器中得到的数据如表3所示。

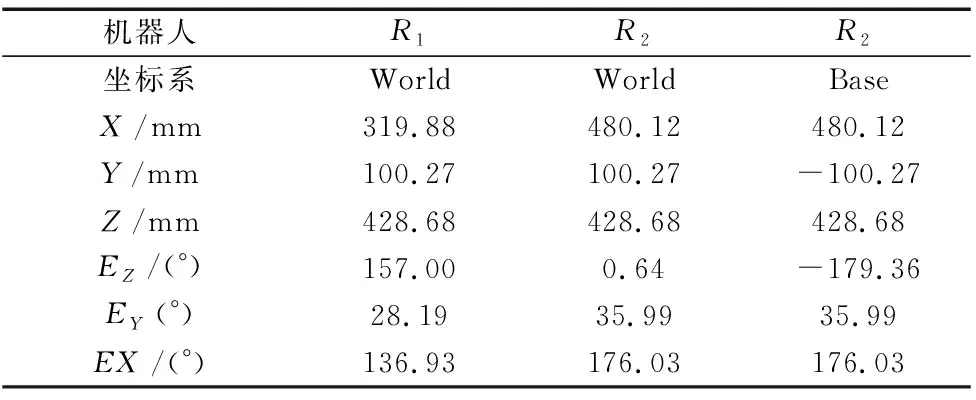
表3 机器人R1和R2的末端位置和姿态

表中的数据显示，主从机器人的末端(标定针针尖)位置相同，但是姿态不同，利用坐标变换让主从机器人末端姿态相同，得到：

(43)

由于主从机器人末端执行器均加上了标定针，可将式(29)变形为：

(44)

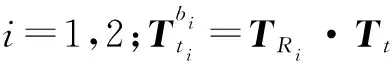
根据表3中的数据，可得：

(45)

(46)

将式(39)、式(43)、式(45)代入式(44)得：

(47)

4 结论

使用改进D-H参数法建立了ABB IRB-120工业机器人的运动学模型，并验证了建立的机器人运动学模型的正确性。提出一种基于标定模型的基坐标系标定方法对双机器人系统进行了标定，在双机器人系统标定的基础上建立了双机器人运动学模型，使用MATLAB和RobotStudio验证了双机器人运动学模型的正确性。研究表明，本文建立的双机器人运动学模型是正确的。