附加约束条件的坐标转换参数求解方法
王骈臻,林 鹏
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
由于研究对象不同,不同的坐标系被建立来准确描述对象的位置信息。这些坐标系的原点定义、坐标轴指向以及单位长度都不尽相同,故相同点位在不同坐标系下有不同的坐标值。当不同坐标系之间发生联系时,需要将点位转换到相应的坐标系内。坐标转换的关键在于求解转换参数,在以往的工作中,线性坐标转换模型经常被用来求取转换参数。张飞等[1]比较了三种常用线性模型的转化结果以及相关系数矩阵。孔钰如[2]基于布尔莎模型分析得出了公共点的个数越多以及分布越均匀,中误差越小的结论。尹慧芳等[3]通过济宁矿区坐标转换实例以及模拟算例得出,七参数线性模型能够有效减小模型误差、提高转换精度,但随着旋转角不断增大,七参数线性模型求解会产生较大的误差。
线性转换模型仅适合旋转角较小的情况,随着测量技术的发展,例如在三维激光扫描方面,点云配准就需要确定任意旋转角下的三维坐标转换参数。面对大旋转角情况下的坐标转换,广大学者进行了无数的探索,曾文宪等[4]将非线性模型线性化产生的误差作为函数模型的模型误差进行处理。姚宜斌等[5]提出了一种不需要知道近似值并且同时适用于大、小旋转角情况的算法。Grafarend 等[6]利用Procrustes 算法来解决七参数坐标变换问题中涉及两个坐标系的随机性度量的合并问题。吕志鹏等[7]用四元数来表示三维旋转矩阵。王世达等[8]提出了三种在无初始值、不需线性化和迭代的条件下,仅通过简单的矩阵运算就可以获得结果的算法,面对不同的角度都有满意的结果。
在传统的七参数转换模型内,旋转矩阵内的九个元素仅有三个是独立的,如果直接解算七参数,过程将非常繁琐。陈义等[9]将参数之间相互独立、非线性的三维坐标转换模型转换为参数之间相互联系、准线性的三维坐标转换模型。马下平等[10]介绍了附有约束条件的大旋转角空间直角坐标转换模型的建立过程,证明了该理论方法的严密性。
综上所述,本文将基于经典最小二乘原理,研究在大、小旋转角情况下,坐标转换参数的约束与非约束解法的效率与精度。
1 实验原理与方法
两个坐标系之间的对称Helmert 转换模型表达式为:
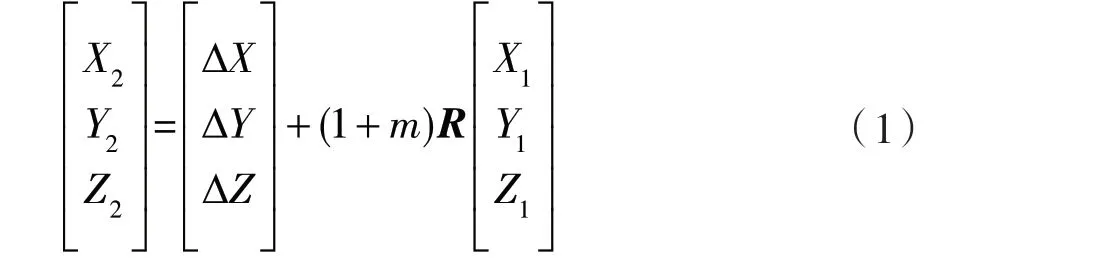
式中,Δ X 、Δ Y 、 ZΔ 为三个平移参数,m 为两个坐标系之间的尺度参数,R 为两个坐标系之间的旋转矩阵。
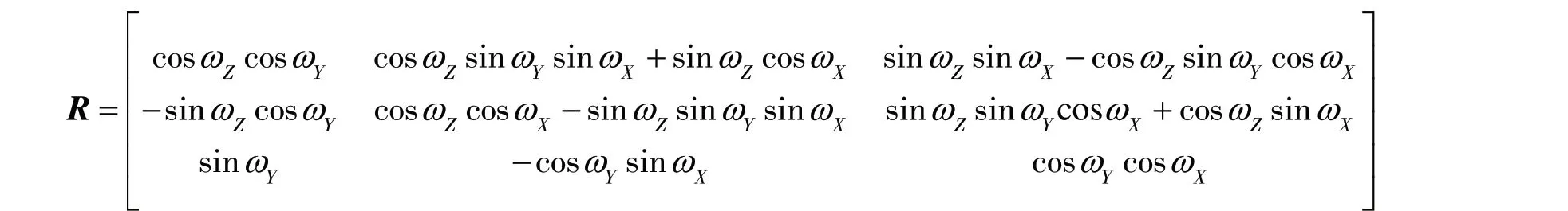
1.1 非约束解法
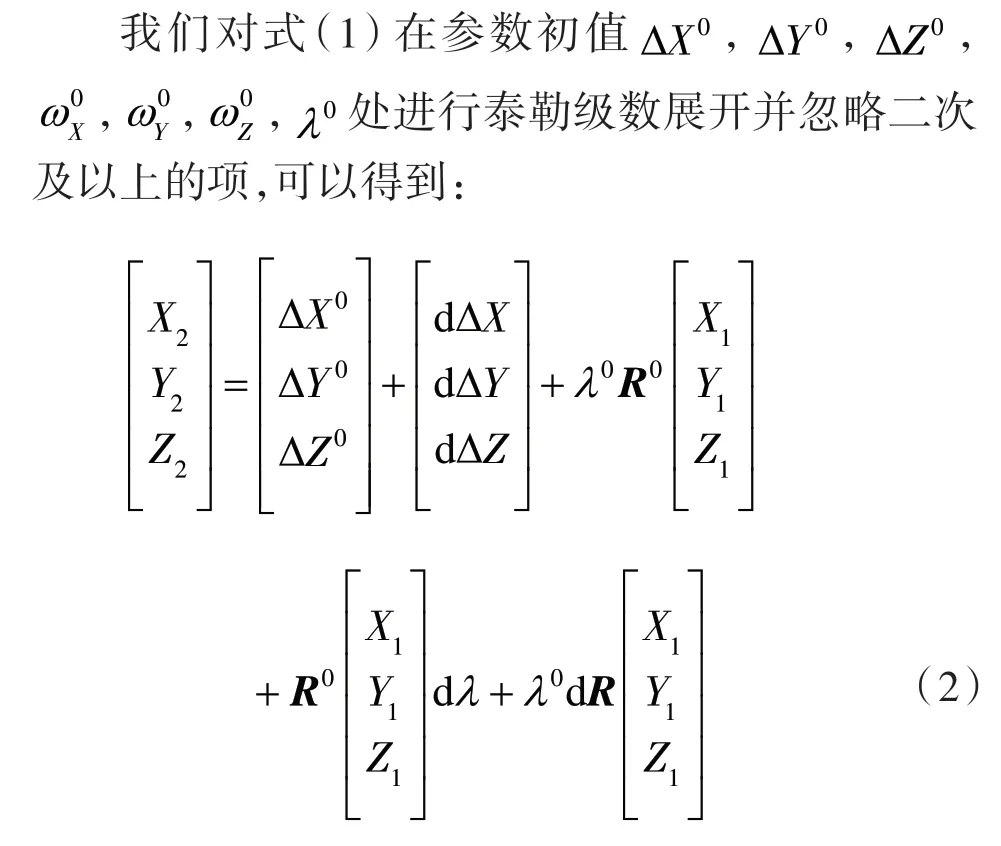
式(2)可归纳为
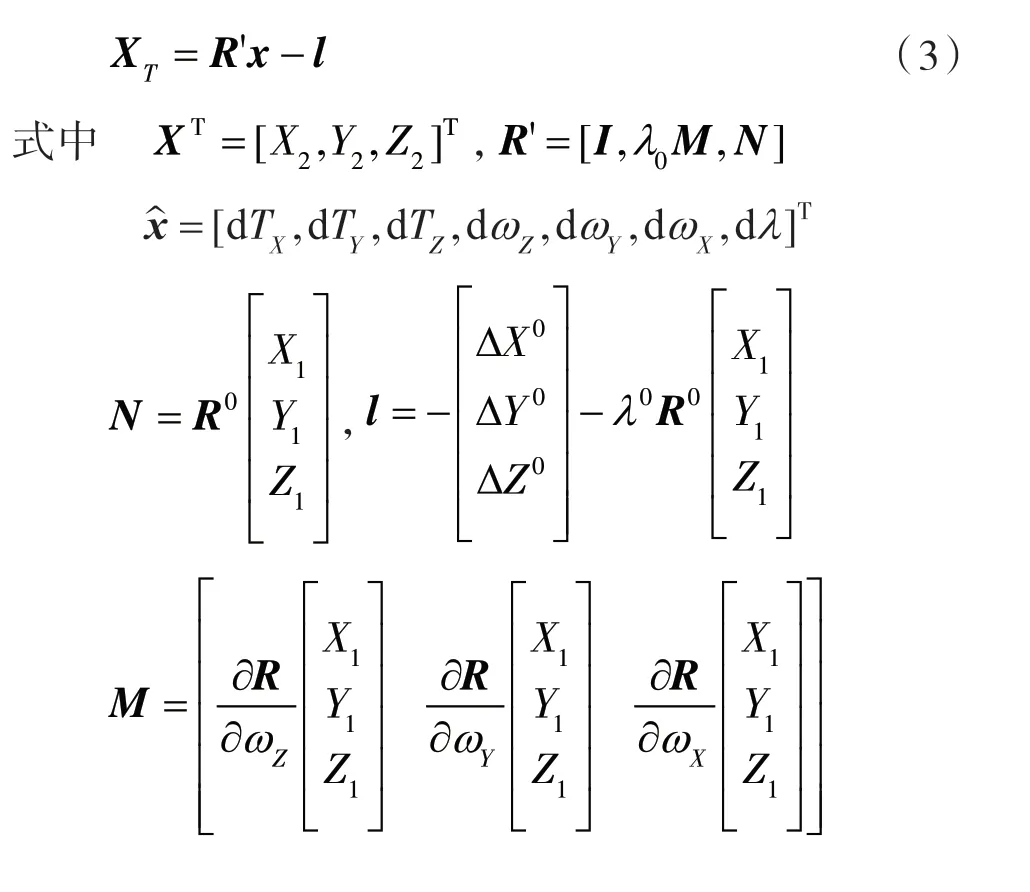

此时,为七参数估值的改正数。为了得到参数的最优估值,可通过最小二平差法则进行迭代计算。
1.2 约束解法
1.2.1 约束条件法
由于非线性七参数模型内有较多关于方向余弦的矩阵,求解过程繁琐。因此有学者提出将旋转矩阵内的九个元素设为参数,直接求取这九个参数。


在这九个参数中,仅有三个是独立参数,其余的六个参数都可以被这三个参数表示。若我们假设2α、3α、3β为独立的参数,剩下的六个参数可以表达为:
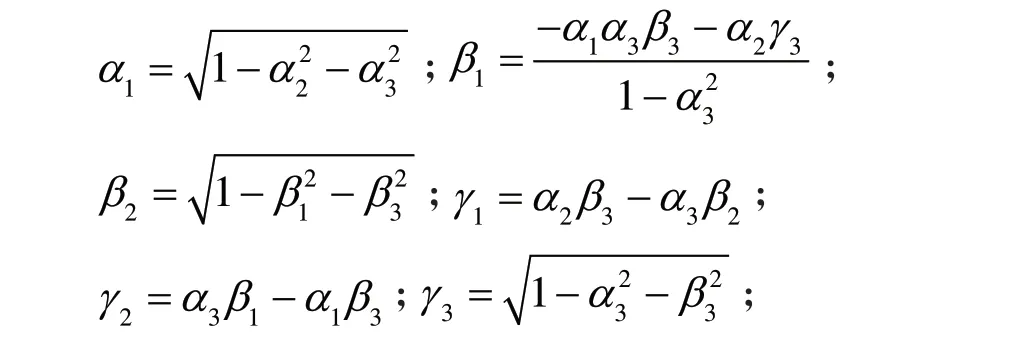
用式(5)替代式(1)中的旋转矩阵R,设待求的参数为三个平移参数,一个尺度参数和九个方向余弦参数。利用泰勒级数对替代后的式子在参数处展开,可以得到:
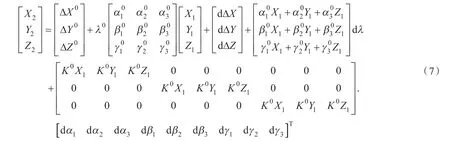
当拥有三个或三个以上公共点时,误差方程的表达式为:

式中:
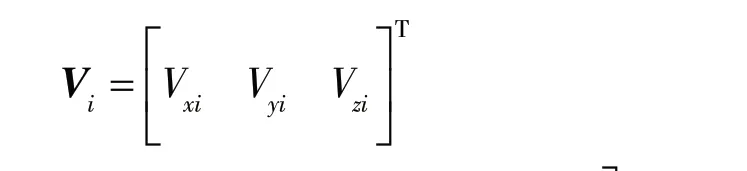

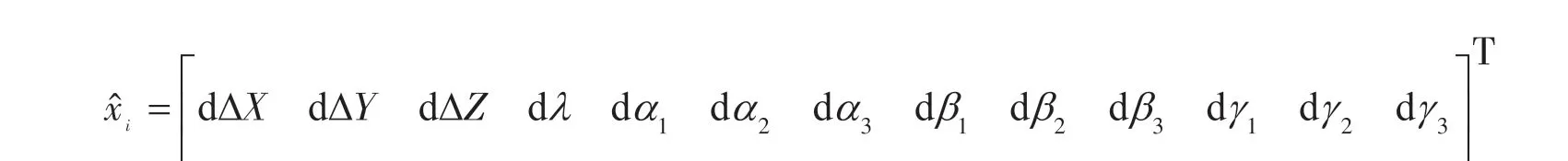
再根据式(6)列出条件方程:

其中, 的含义与式(8)相同。C 与W 分别为:
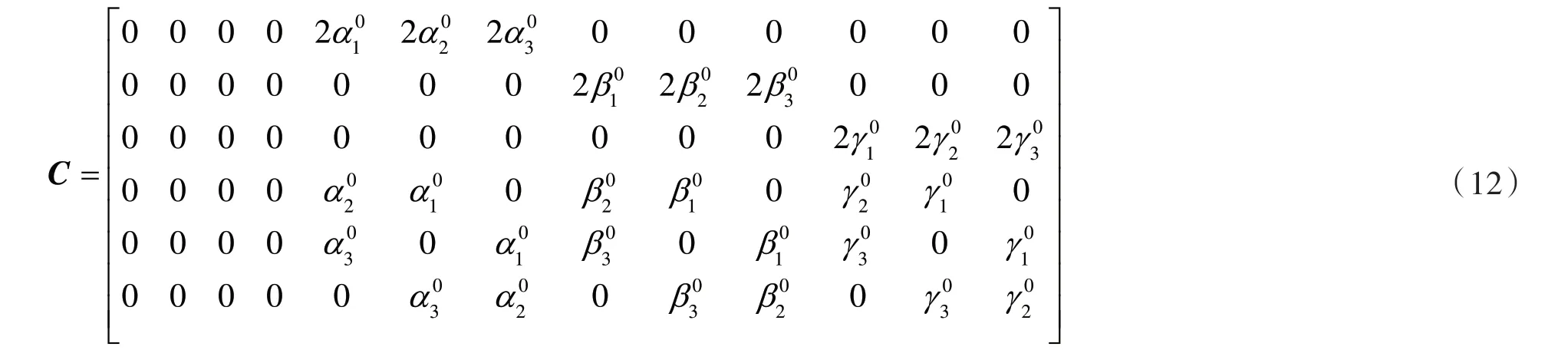
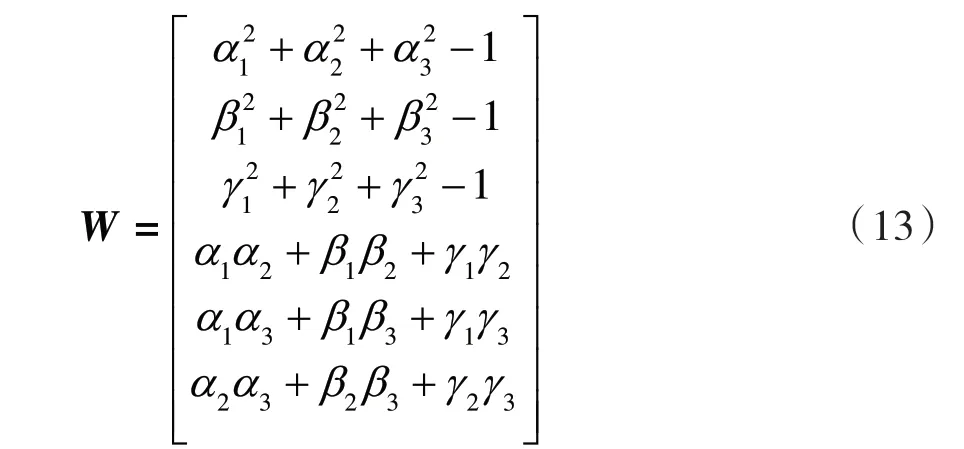
此时可利用最小二乘原理进行迭代计算来求解参数的最佳估值。
1.2.2 虚拟观测值法
虚拟观测值法的基本思想是将设计矩阵中含有测量误差的元素当作虚拟观测值,在原有误差方程的基础上增加虚拟误差方程,同时将设计矩阵中含有误差的元素在新算法中当作参数求解[11]。虚拟观测值法将附有约束条件的间接平差问题简化为经典间接平差问题,简化了计算步骤,使得计算更加方便。
本文将约束条件方程内的元素视为无误差,即约束条件方程元素的权无限大。在计算时可使用相对较大的数字替代,本次实验将约束条件元素的权设为1012。则虚拟观测值法的权阵P1为:
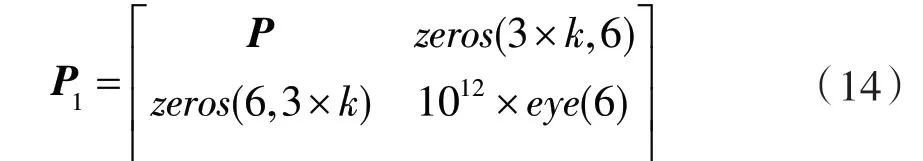
式中P为观测方程的权阵,k 代表公共点个数,zeros(n,m)代表一个n 行m 列的零矩阵,eye(q)代表一个q 维的单位矩阵。
当拥有三个或三个以上公共点时,可列出误差方程:

Ai为式(9)与式(12)的上下叠加矩阵,Li为式(10)与式(13)的上下叠加矩阵。
此时便可根据最小二乘原理进行迭代计算来求解参数的最佳估值。
2 实验分析
本次实验分为两部分:第一部分是在小旋转角情况下解算转换参数;第二部分是大旋转角情况下解算转换参数。实验步骤如下:
(1)仿真19 个点的源坐标系坐标,任取18 个点作为公共点参与解算,剩下的点作为检核点,给出七参数的真值,得到点位在目标坐标系内的坐标真值。
(2)随机生成各点的中误差,利用随机函数给真值加上误差,生成观测值,共生成1 000 次。设先验权中误差为σ0,则每个坐标的定权情况分别如下:
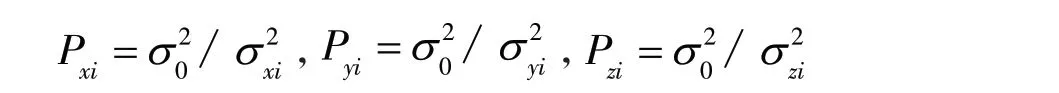
(3)利用外推点验证解算参数的精度。
(4)采用均方根误差作为精度评定的标准,迭代收敛阈值为10-8。
2.1 实验一(小旋转角)
假定源坐标系与目标坐标系之间的七个转换参数分别为 ΔX =1 000 m, YΔ =1 000 m,Δ Z =-1 000 m,λ=1.000 000 1(尺度参数),α=0.5″,β=0.5″,γ=0.5″。对各模型求取的参数估值与参数真值之间求取均方根误差,结果见表1。为了更好地进行比较,将十三参数进行了还原。
在旋转角比较小的情况下,线性布尔莎模型由于近似替代而造成的误差非常小。而非线性模型由于旋转矩阵本身的非线性特性,在起初就削弱了近似替代产生的误差,而且泰勒展开产生的误差非常小,可以忽略不计。结合表1 内容,可以得到线性化模型和非线性化模型都适用于旋转角较小时的坐标转换参数求解。
图1 给出了外推点分别在三个坐标转换模型下的差值序列。从图1 中我们可以看出,利用线性布尔莎模型、非线性七参数模型和非线性十三参数模型所求参数转换的点位坐标在X、Y、Z 方向的差值序列的范围分别在-0.05~0.05 m、-0.05~0.05 m、-0.05~0.05 m,说明虽然线性模型较非线性模型没那么严密,但是在小角度的情况下还是适用。
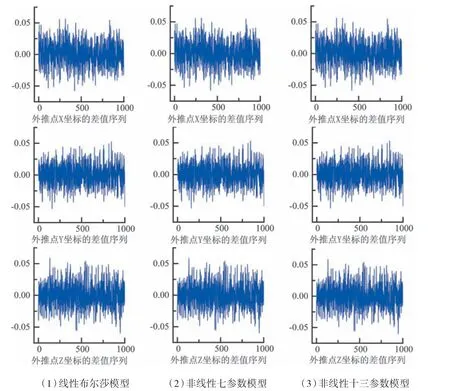
图1 小旋转角下外推点的差值序列
图2 是各模型的单次计算时间汇总。从图2 我们可以得到,小角度情况下,布尔莎模型单次计算时间的范围在0.000 15~0.000 6 s 之间,非线性七参数模型单次计算时间的范围在0.000 6~0.001 75 s之间,非线性十三参数模型两种计算方法分别在0.000 3~0.002 5 s 以及0.001~0.003 s 之间。再结合表1 内各模型计算得到参数的均方差以及各计算模型的平均迭代次数,可以得出,在旋转角较小的情况下,比较适合使用布尔莎模型来进行计算。

表1 小旋转角(三维坐标转换)转换参数的均方根误差

图2 小旋转角下各模型单次仿真计算时间
2.2 实验二(大旋转角)
设源坐标系和目标坐标系之间的7 个转换参数分别为 ΔX =1 000 m,ΔY =1 000 m,ΔZ =1 000 m,λ=2,α=36°,β=36°,γ=36°。对各模型求取的参数估值与参数真值之间求取均方根误差,结果见表。为了更好地进行比较,将十三参数进行了还原。
我们可以从表2 中得出:
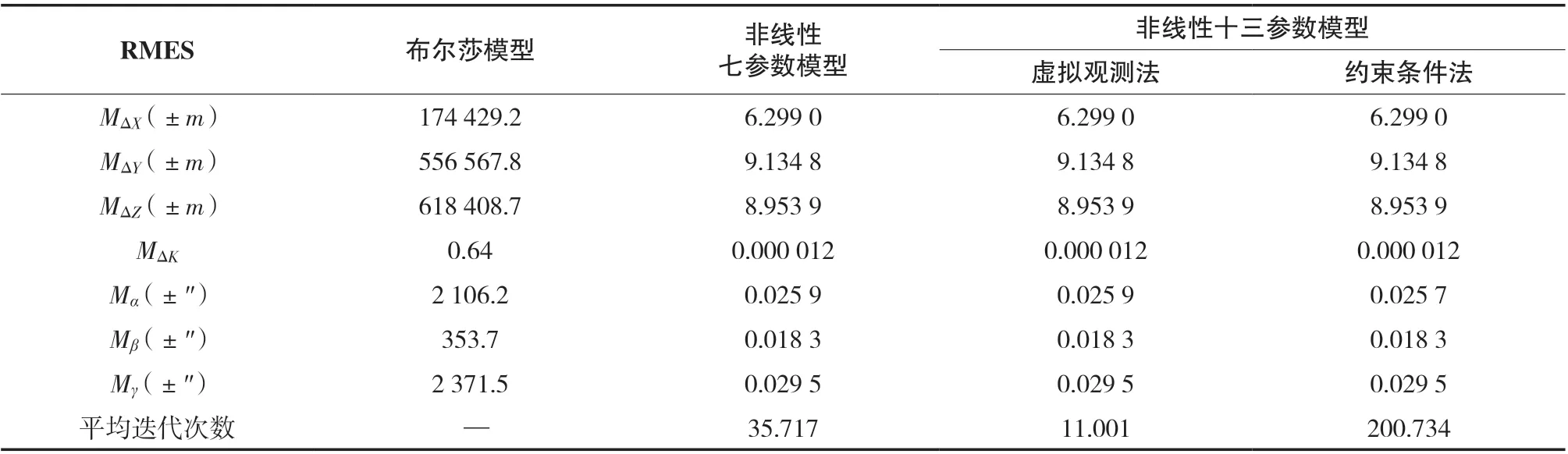
表2 大旋转角(三维坐标转换)转换参数的均方根误差
(1)在旋转角较大的情况下,线性布尔莎模型求得的七个参数估值严重偏离真值。而非线性十三参数模型与非线性七参数模型求得的参数与真值较为接近,且这两个模型求得的参数估值一致。
(2)从均方差的结果来看,两种非线性模型的均方差值一致。这是因为这二者的本质都是利用泰勒展开对坐标转换公式进行线性化并且只保留一次项,所以这两个模型的精度是一样的。
(3)从迭代次数上来看,虚拟观测值法所需的迭代次数要远少于非线性七参数模型,这是因为虚拟观测值法优化了系数矩阵,使得计算更加简便。
在图3 中,我们可以看到布尔莎模型解算的外推点的坐标在X、Y、Z 三个方向的序列差值分别为99 690~99 710 m、109 005~109 025 m、137 400~137 450 m,转换得到的参数与真值严重不符合,再次证明了布尔莎模型仅在旋转角较小的情况时适用。非线性七参数模型和非线性十三参数模型解算的外推点坐标在X、Y、Z 三个方向的序列差值分别为-0.15~0.15 m、-0.15~0.15 m、-0.1~0.1 m。可以得出,在大旋转角情况下,非线性模型推算的点坐标与真值之间的差距很小。
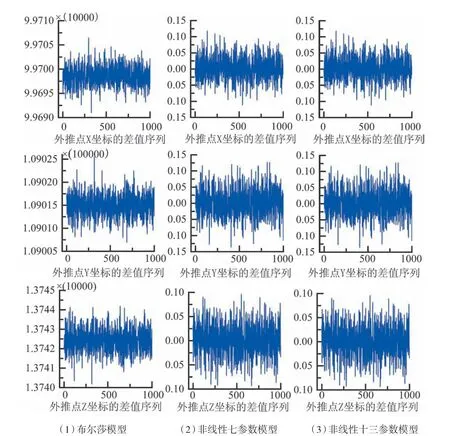
图3 大旋转角下外推点的差值序列
图4 内是各模型在大旋转角情况下单次仿真的计算时间。从图4 内我们可以看出,在大旋转角的情况下,非线性七参数模型、虚拟观测值法以及约束条件法的单次仿真计算时间范围分别集中在0.004~0.04 s、0.002 25~0.005 s、0.003 9~3 s 之间。在三种计算方案中,虚拟观测值法的计算时间最短,它的计算效率比非线性七参数模型提高了约500%,比约束条件法提高了约1 500%。
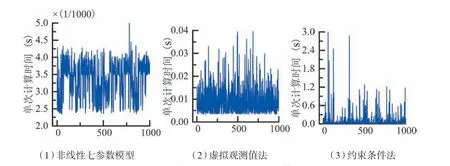
图4 大旋转角下各模型单次仿真计算时间
综上所述,在大旋转角的情况下,非线性十三参数模型(虚拟观测值法)比较适合用来求解转换参数。
3 总结
文中利用仿真模拟现实观测值,分别在大、小旋转角情况下进行坐标转换模型约束与非约束解法的计算,并利用外推点来检核解算的参数,与真值进行比较,对转换参数精度进行分析。实验结果表明:线性模型仅适合小旋转角情况下的坐标转换;在大旋转角情况下,非线性十三参数解法(虚拟观测值法)更适合来解算转换参数。

