T 形截面悬臂柱自重下弯扭屈曲无穷级数解与FEM 验证

张文福，吴 宇，黄 斌，杭昭明

（1.安徽建筑大学 土木工程学院，安徽 合肥 230601；2.南京工程学院 建筑工程学院，江苏 南京 211167；3.东北石油大学 土木建筑工程学院，黑龙江 大庆 163318）

T 形截面是钢结构轴心受力构件中的一类重要的截面形式。T 形截面构件可通过焊接、轧制或H 型钢剖分获得，具有易加工的优点，广泛应用于钢结构轴压构件中，而其在轴压作用下容易发生弯扭屈曲，需要对其稳定承载力进行分析。

国内外学者对薄壁T 形截面构件轴压稳定性的研究主要集中在理论、有限元模拟以及规范对比方面。Mohri[1]研究了包括T 形截面在内的薄壁构件受压的后屈曲平衡曲线。郭兵等[2]分别对T 形截面轴压钢构件的翼缘和腹板做了屈曲分析，提出了翼缘和腹板的宽厚比限值公式。申红侠[3]研究了《钢结构设计规范》（GB50017-2003）所提出的焊接T 形截面轴心压杆弯扭屈曲的换算长细比法，使用有限元分析软件ANSYS 验证了规范的合理性。熊晓莉等[4-5]提出了一种T 形截面压杆设计计算的新方法——折算长细比法，并研究了剖分 T型钢压杆轴向压力分别作用于形心和剪心时的整体稳定性。吴金池等[6]归纳总结了中、美钢结构规范关于双角钢T 形截面构件受压稳定承载力设计方法的差异。近年来关于薄壁构件有限元分析方法和理论研究也有所进展。张磊等[7]提出了壳体单元模型精确模拟薄壁构件整体稳定性的方法。张文福[8]以双轴对称的工字形轴压钢柱为例，在Kirchhoff 薄板理论和Euler 梁理论的基础上建立了一种开口薄壁构件弯扭屈曲新理论。对于矩形悬臂柱因自身重量而屈曲的问题，即著名的“旗杆问题”，自重产生的轴向压力沿着杆长方向连续分布，对应的屈曲平衡方程是变系数的微分方程，通常采用能量法、有限单元法等近似方法求解。张文福[9]采用能量变分法，运用Matlab 计算软件得到了矩形悬臂柱自重荷载下位移函数取50 项的弯曲屈曲精确解。

本文基于板-梁理论[10]和能量变分原理[11]解决了T 形截面悬臂柱在自重下的弯扭屈曲问题，得出了T 形截面悬臂柱在自重作用下的弯扭屈曲荷载。运用ANSYS 有限元分析软件验证理论计算结果，结果表明了理论的正确性，可为工程设计提供参考。

1 理论计算

1.1 板-梁理论

以图1 所示的T 形截面柱为研究对象，引入了两套坐标系：整体坐标系xyz 和局部坐标系nsz。这两套坐标系与Vlasov 坐标系类似，均符合右手螺旋法则，整体坐标系的原点选在截面形心C，各板件的局部坐标系原点选在板件形心。

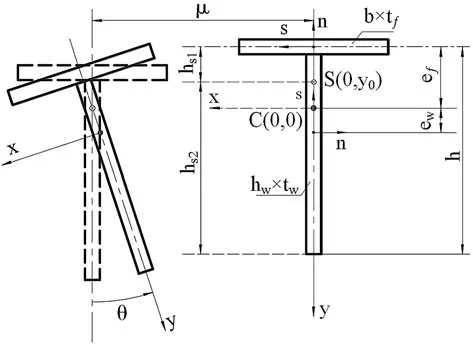
图1 T 形截面的坐标系与变形图

已知：钢柱的长度为L；翼缘的宽度为b；厚度为tf；翼缘的弹性模量为Ef，剪切模量为Gf，泊松比为μf；腹板的高度为hw，厚度为tw；腹板的弹性模量为Ew，剪切模量为Gw，泊松比为μw。

T 形截面柱的总应变能可表示为

1.2 弯扭屈曲无穷级数解

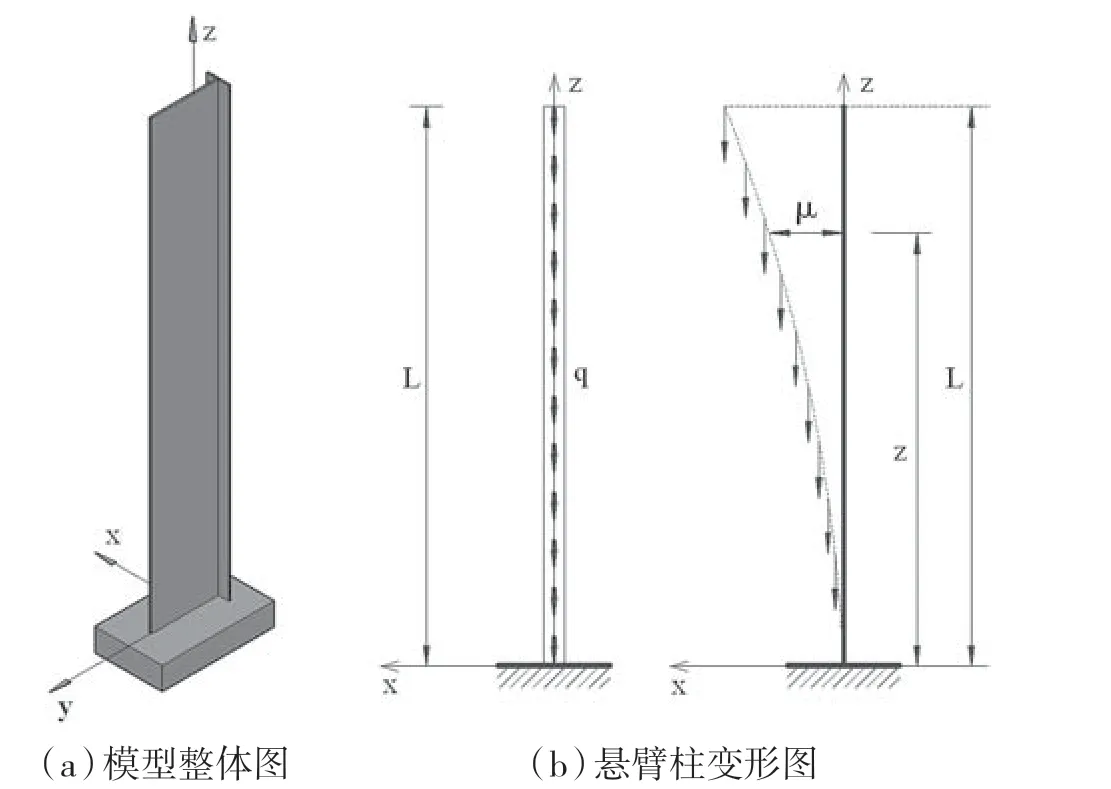
图2 自重下T 形截面悬臂柱计算简图

将式（15）～（18）代入式（12），根据势能驻值原理，即作用着外力的结构体系，其位移有微小变化而总的势能不变，即总的势能有驻值时，则该结构体系处于平衡状态，可表示为

上述方程的解即为所求单轴对称T 形截面悬臂柱受轴向压力发生弯扭屈曲时的临界屈曲荷载。

2 有限元验证

2.1 建立有限元模型

2.1.1 选择单元

借助有限元分析软件ANSYS 对自重荷载作用下的T 形截面悬臂柱的屈曲行为进行数值模拟。为了精确模拟薄壁构件整体稳定性，单元选用4 节点有限应变壳单元SHELL181。

2.1.2 定义几何参数和材料本构关系

柱高为L，T 形截面腹板高为hw=0.3 m，厚度为tw=0.008 m，翼缘宽度为b=0.1 m，厚度为tf=0.006 m，钢材取Q235 型号的钢材，弹性模量Es=1.06×105MPa，泊松比为μs=0.3。

2.1.3 建立几何模型并划分网格

有中国学者尝试对中国专利法的“平行进口”问题进行理论阐释时，认为虽然中国专利法承认了平行进口的合法性，但应该以“默示许可理论”来作为这一条的理论基础，而不应该适用权利用尽理论。例如严桂珍教授即主张“我国的实际情况表明，在允许平行进口的基础上，我国应当选择采用默示许可原则。”其理由是，“采用默示许可，权利人又可以通过合同限制排除权利用尽原则的适用，使权利人拥有一定的权利，不至于过于被动。而且，是否存在默示许可，又是由法院个案认定，最终由法院掌握规制专利平行进口的主动权，从而达到原则性与灵活性相结合的效果。” [10]

建立一个腹板高为hw，厚度为tw，翼缘宽度为b，厚度为tf的T 形截面柱，如图3 所示。

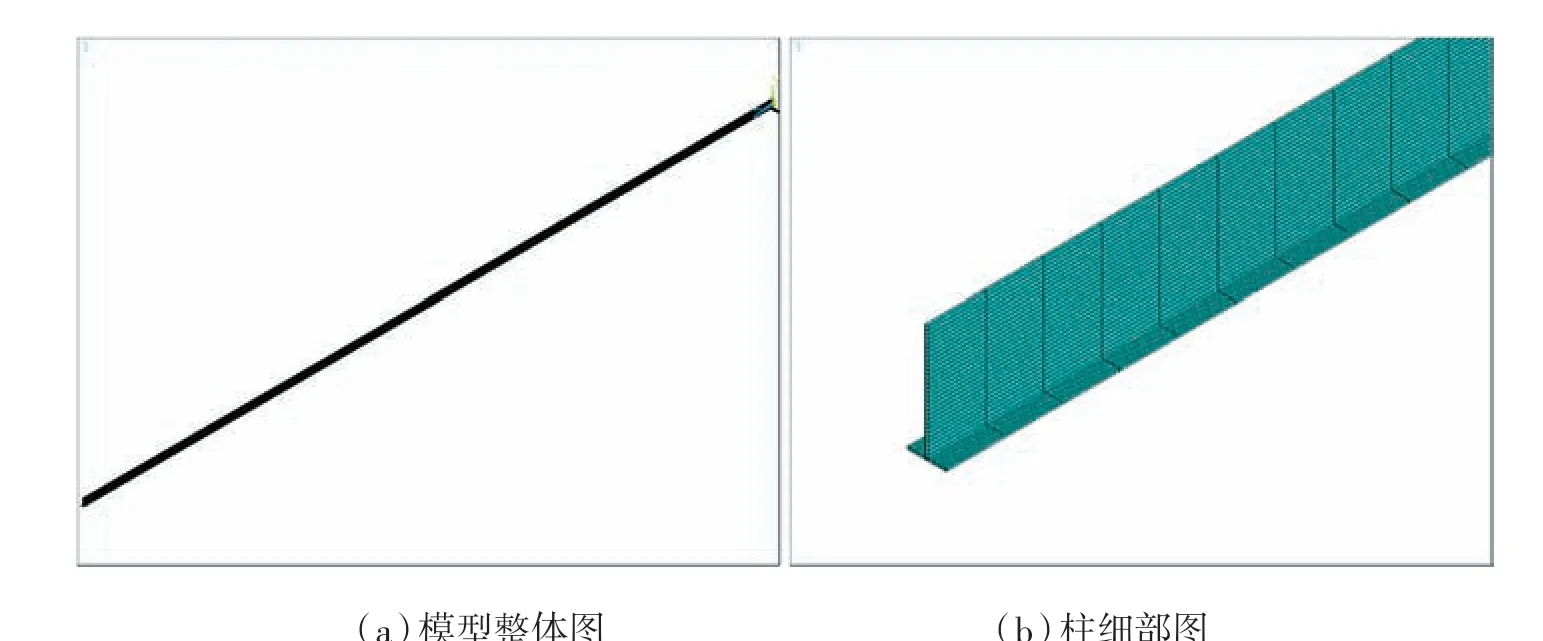
图3 模型概况

2.1.4 施加约束

有限元模型模拟悬臂柱，需模拟一端固定的边界条件，即限制一端全部节点的3 个平动和3 个转动自由度，如图4 所示。

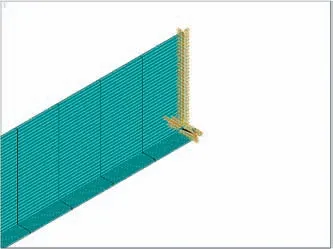
图4 约束边界条件图

2.1.5 施加荷载

通过对模型上所有的节点施加单位荷载1 来模拟柱体所受的自重荷载，如图5 所示。

图5 荷载施加情况

2.1.6 求解

根据有限元屈曲分析的一般步骤，先进行静力分析，再选择ANTYPE，BUCKLE 命令进行特征值屈曲分析。

2.1.7 后处理

后处理器可导出弯扭屈曲模态图和屈曲荷载系数表，最终的屈曲荷载为最小屈曲荷载系数与所施加的荷载的乘积。由图6（c）断面图可以看出截面发生了侧向弯曲屈曲以及扭转，即为T 形截面悬臂柱轴压作用下的弯扭屈曲模态。

图6 屈曲形态图

2.2 有限元验证

本文较为细致地分析了长细比因素的影响，分别建立了长细比为50、100、150、200、250、300 的6组悬臂细长柱有限元模型，屈曲荷载有限元模拟结果与理论推导所得的结果如表1 所示。

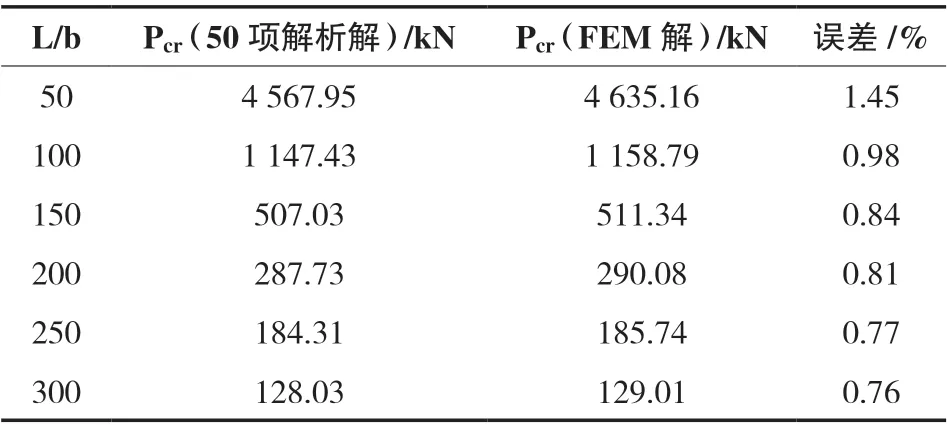
表1 有限元结果与理论结果的对比

从表1 可看出，本例中公式推导所得到的结果与有限元结果的误差均在1.5%以内，已经完全达到工程计算对精确度的要求。并且，两者的误差随着长细比的增大而减小。

3 结论

（1）板-梁理论可以求解自重荷载作用下的轴压构件屈曲荷载，并且对于长细比大于50 的细长T 形截面悬臂柱误差在1.5%以内，精度较高。

（2）ANSYS 有限元软件中SHELL 单元适合用于分析薄壁构件，T 形截面悬臂柱在自重荷载作用下发生弯扭屈曲，与理论假设相一致。

（3）板-梁理论根据经典理论将薄壁构件各板件的屈曲变形分解为平面内的弯曲变形和平面外的扭转变形，并分别按Timoshenko 梁和Kirchhoff板力学模型确定，根据能量变分原理计算求解。相较于传统Vlasov 理论，物理过程清晰明确、容易理解，适合薄壁构件的屈曲分析。