盾构下穿施工对既有城市道路沉降影响研究
南 钰,严 中,陈 凯,翟朝娇
(1.安徽建筑大学 土木工程学院,安徽 合肥 230601;2.合肥市市政设计研究总院有限公司,安徽 合肥 230041;3.中铁二十四局集团安徽工程有限公司,安徽 合肥 230011)
在城市化进程的加速推动下,地面交通已不能满足人们日常出行需要,因此在大中型城市建设地下轨道显得至关重要[1]。由于大中型城市地铁线路密度大,且市区范围内公路、铁路及管道分布密集,在复杂地质条件以及日渐增加的地下空间利用率下合理施工成为我们研究的关键。
盾构下穿对既有结构影响的研究近年来已经取得了不小的成就,并且指导了多个相关工程案例顺利实施。20 世纪60 年代,Peck[2]研究得出,地面以U 型槽形式发生沉降,基于对大量数据的分析,提出了Peck 公式。甘晓露等[3]利用Pasternak 弹性地基梁模型和 Loganathan-Polous 解,证明了隧道间距变化会引起地表沉降和隧道弯矩变化。王忠凯等[4]在运用应力路径法预测地表变形的基础上,结合隧道间距和沉降的关系,证明了应力路径法的特殊性。杜明芳等[5]基于洛阳市轨道交通2号线的现场监测数据,对大粒径卵石地层中盾构开挖对上部道路沉降影响规律进行研究。宋卫东等[6]通过建立三维数值模型,揭示了在盾构开挖过程中,土体的竖向和横向位移都会由于挤压作用而产生变化,且开挖面附近最为剧烈。赵丽雅等[7]研究并总结了铁路轨道走向与地表沉降变化之间的关系,并得出可以通过增大注浆体弹性模量的方式来减小地表变形。
以上研究主要论证隧道间距,隧道所处地层性质以及隧道周围注浆条件等因素对道路沉降的影响,但目前涉及作为主要影响因素的隧道埋深和开挖距离的研究还不充分,为此,本文将针对这两种因素下的各类工况,基于数值分析的方法,揭示盾构下穿施工时城市道路的沉降规律,以期为国内类似工程案例提供参考和借鉴。
1 工程概况
以合肥市轨道交通四号线天水路站—翠柏路站盾构区间工程为依托,区间分别经过合肥东编组站及其北侧空地、规划铜陵北路到达翠柏路站。盾构隧道内径为Φ5 400 mm,管片厚度为300 mm,宽度为1 500 mm,管片混凝土为C50P10。共观测到两层地下水,地下水类型为上层滞水、基岩裂隙水。盾构区间标准断面及土层物理力学性质参数如图1 和表1 所示。

表1 土层物理力学性质参数
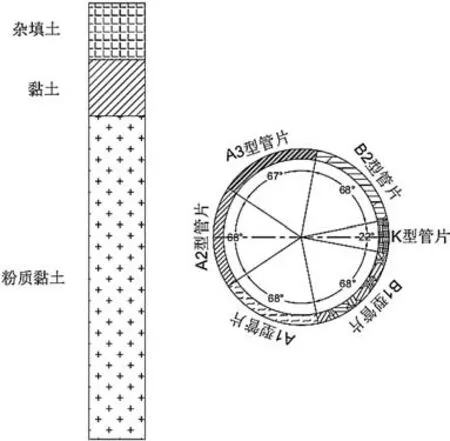
图1 盾构区间标准断面图
2 有限元模型建立
2.1 计算模型建立
本模型各参数确立拟依据现场施工情况。为了满足隧道开挖的边界条件,依据圣维南原理,在隧道周边填充的边界应不小于隧道外径的三倍且不大于隧道外径的五倍[8]。为了尽量减小边界效应的影响,本模型长度取10D=60 m(左右边界各取4.5D),宽度取5D=30 m,总高度取7D+0.8 m=42.8 m(上下边界各取3D)。本模型最上部为一层厚度0.8 m 的路基,路基下为四种不同性质的土层,自上而下分别为杂填土、黏土、粉质黏土、全风化泥质砂岩,厚度依次为3 m、3 m、26 m、10 m。隧道拱顶至地表距离为12 m,隧道间距为12 m。按照上文对模型的描述,建立如图2 和图3 的模型。

图2 道路与隧道相对位置图

图3 注浆环视图
模型有32 125 个单元,150 831 个节点。其中土层和路基采用修正-摩尔库伦本构关系,管片、盾壳等均视为线弹性本构模型[9]。施工过程中依次采用改变属性功能将注浆层原先为土体的地方更改为注浆材料属性。前、后、左、右四个边界面采用法向约束,模型最下层施加纵向位移约束以起到约束土层不横向变形的作用[10]。各材料物理力学性能参数(参考现场施工报告和资料)如表2所示。

表2 各材料物理力学性能参数
2.2 施工过程模拟
本模型全长30 m,每次开挖一环管片衬砌,宽度为1.5 m,且左线先行。开挖过程中盾构外壳先行,注浆和开挖区域同时钝化,并激活作用在下一开挖面上的掌子面压力。在此基础上,每条线开挖从第二步开始,都要依次激活管片、千斤顶力和注浆压力,并且将原注浆区域的参数转化为注浆材料,同时钝化前一阶段的盾构外壳和千斤顶力。
2.3 计算工况
为了研究隧道在不同埋深以及开挖不同距离时,盾构施工对既有城市道路沉降变形影响,拟采用不同工况进行分析,不同埋深的工况(保持隧道间距恒定,埋深取1.5D~3.5D 范围内偶数值)如表3 所示。
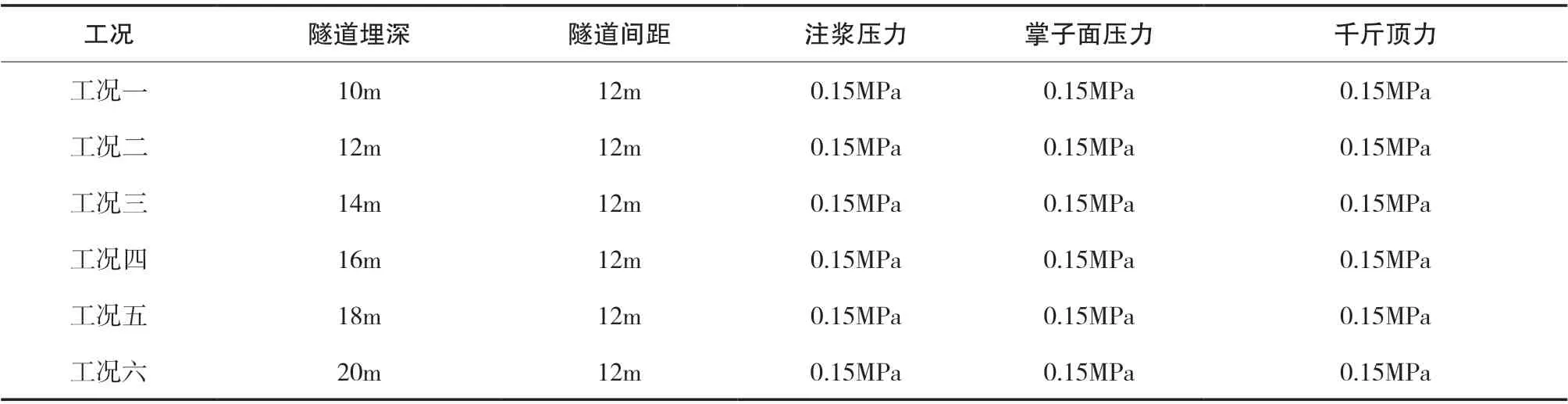
表3 计算工况
同时,固定隧道埋深和间距均为12 m 时,按照先开挖左线的顺序,每开挖7.5 m 设置一个工况,直至全线贯通。
2.4 模型验证
通过实测及模拟数据的对比,验证了模型的正确可行性,对比结果如图4 和图5 所示。由图可知,不论是在左线贯通还是全线贯通时,所得到的规律曲线都是保持相同的形态(左线“单谷”,全线“双谷”),且左线贯通的最大沉降差不超过2 mm,全线贯通的最大沉降差不超过3 mm,均不超过实测沉降最大值的30%[11]。这是由于实际施工中土体参数和施工方式的各项差异导致,在合理范围内。因此,本数值分析模型基本符合实际施工情况。
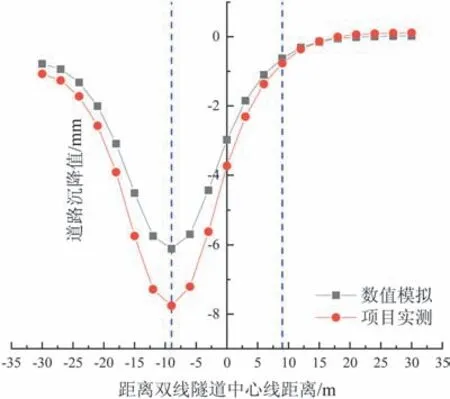
图4 左线贯通时Y=0 断面处路基沉降曲线
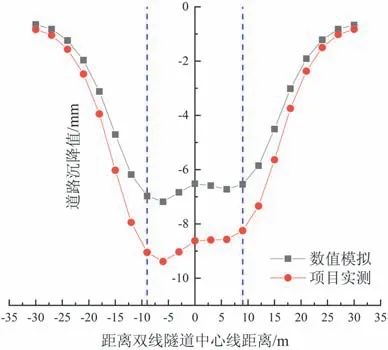
图5 双线贯通时Y=0 断面处路基沉降曲线
3 计算结果分析
3.1 隧道开挖距离的影响研究
为有效控制施工过程中隧道上方土层的变形,在隧道埋深为12 m、间距为12 m 的条件下,研究不同开挖距离与路基沉降之间的规律。通过分析不同工况下路基的沉降数值,可以得到如图6 所示的沉降值对比图以及路基沉降结果汇总表4。

表4 路基沉降结果汇总表
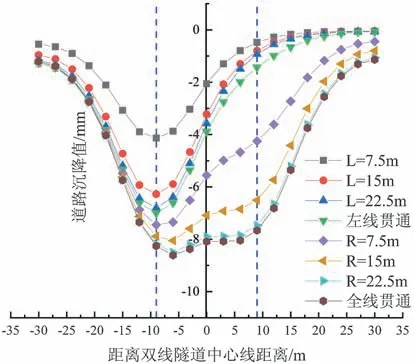
图6 不同开挖距离下的路基沉降对比图
通过研究表中数据变化可知,当左线开挖到第五环也就是7.5 m 处时,左线隧道上方的路基部分已经出现了显著的沉降,量值为4.13 mm;开挖不断加强土层扰动,从7.5 m 到15 m 的过程中扰动最强,从4.13 mm 突增至6.80 mm,沉降量差值超过了2 mm,而此后每一步最大沉降差值都不超过0.6 mm。这说明隧道在初始开挖阶段对上部土体变形的影响要大于开挖深入阶段,原因是随着管片的拼装,注浆总压力增大,注浆部分的浆液也逐渐凝结,从而限制了上部土体的下沉。
由图6 可知,随着左线开挖完成,路基最大沉降的位置仍然在左线隧道中心线处,但右线隧道上方土体也开始出现少量沉降。并且随着左线贯通,右线隧道开挖,路基沉降的最大值逐渐向双线隧道中心线方向移动,沉降值由两侧隧道向双线隧道中心线处减小,这是由于双线隧道开挖过程中,左右隧道之间的土体可能会产生垂直地面向上的挤压作用。并且左线隧道上部的土体始终保持着一定的下沉速率,这说明隧道开挖并非是各自独立的。
3.2 隧道不同埋深的影响研究
周围土体会因为开挖的推进而受到扰动,从而产生地层损失,而这种损失传递到地表则产生了沉降。现将隧道埋深依次取为10 m、12 m、14 m、16 m、18 m、20 m,并将工况一至六依次添加进模型计算,分别得到各工况下的路基沉降对比图,如下图7 和8 所示。
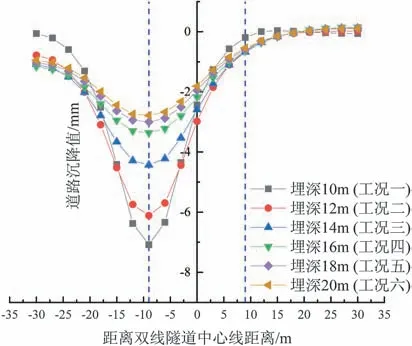
图7 左线贯通时六种工况下路基沉降值对比图
如图7 所示,当左线全部贯通之后,沉降最大值出现在左线隧道中心处。隧道对上部路基沉降的影响随着埋深的增大越来越小,曲线峰值不断减小,从7.08 mm 减小到2.68 mm,并且发现沿X 轴正方向距离左线中心线左侧最远处的沉降量始终大于距离左线中心线右侧最远处的沉降量,这说明离盾构隧道越近的土层受到施工的影响越大。
从图8 看出,全线贯通时,当隧道埋深较浅,沉降曲线呈现“双谷”的形式[12],并且“谷底”始终分布在左右线隧道中心处。同时随着埋深的增大(从10 m 增加到20 m),“谷峰”逐渐平缓,沉降槽逐渐增大,说明盾构施工对土层的影响逐渐减小。当埋深达到14 m 时,曲线又重新恢复为“单谷”形式。同时,从图中也可以明显看出,在埋深为10 m时,最大沉降值出现在左线隧道中心处。而随着埋深增大,最大沉降值位置逐渐平移到双线隧道中心处,这说明先行隧道上部土体会受到来自后行隧道开挖过程的影响,从而导致累计沉降量始终较大(埋深从10 m 到20 m 的过程中,左线隧道中心处沉降量占双线最大沉降量的比例是93%~67%)。但当埋深大到一定程度时,这种影响几乎可以忽略,届时最大沉降的位置一定是出现在两隧道中心线正上方。表5 统计了六种埋深下路基的沉降结果。
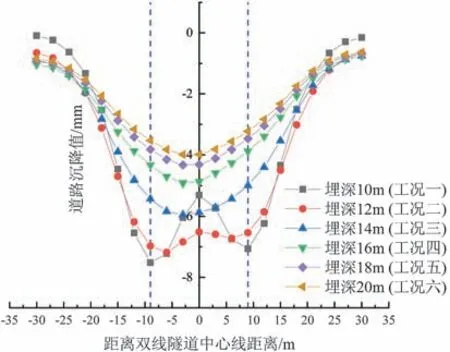
图8 全线贯通时六种工况下路基沉降值对比图
由表5 可知,全线贯通时的路基沉降最大值始终大于同埋深下的左线贯通,并且随着埋深的增加,全线贯通时沉降曲线的沉降槽宽度也在逐渐增大,说明对上部路基的影响越来越小。
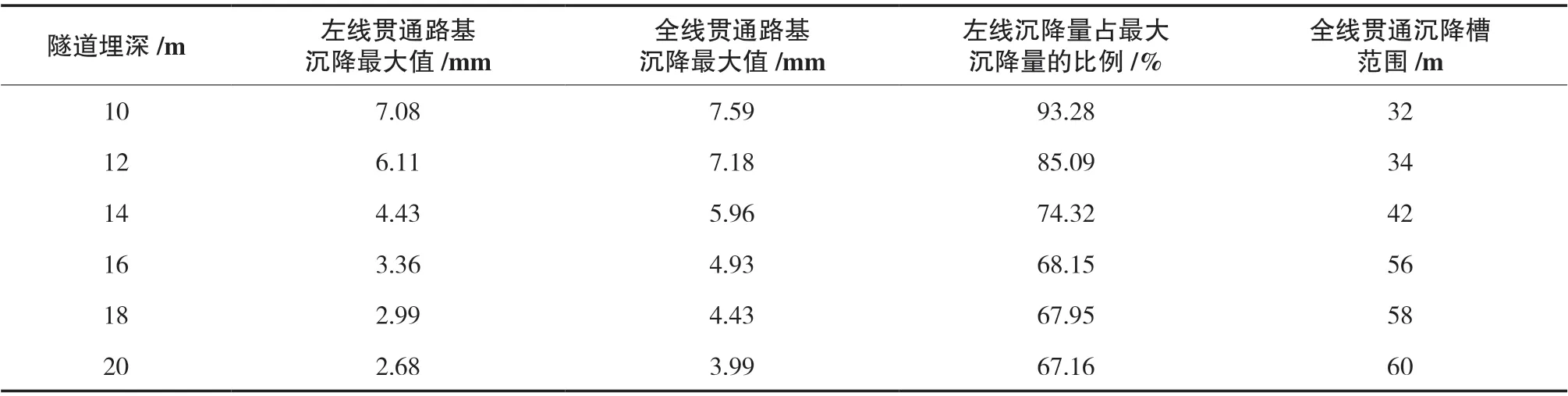
表5 六种隧道埋深下路基沉降结果统计
4 结论
本文主要采用数值模拟的方法,以合肥轨道交通四号线天水路站—翠柏路站区间工程为依托,对隧道在不同埋深和不同开挖距离下对城市道路产生的影响进行研究,得出主要结论如下:
(1)左线隧道在开挖第五环到第十环内,沉降差值最大。超过2 mm,并且随着右线隧道开始动工,路基沉降最大值逐渐向两隧道中心线方向移动。
(2)由于开挖过程中双线隧道间的互相作用,导致埋深在2D 以内时,隧道间的土体会受到挤压而向上移动,使得沉降曲线随着开挖的进行逐渐变为“双谷”形式,但沉降峰值始终出现在左线隧道中心线附近。
(3)当埋深增加至2D 到3.5D 之间时,左线贯通的曲线峰值出现在左线隧道中心线处,全线贯通的曲线峰值出现在双线隧道中心线处并且埋深与影响范围成正比,与影响程度成反比。本文仅研究了埋深在1.5D~3.5D 的情况,建议增加隧道埋深的范围,并研究施工时的其他参数对路基沉降有何种影响。

