度量G-空间中G-强链回归点集的拓扑结构

冀占江, 贝彩霞

(1. 梧州学院 大数据与软件工程学院, 广西 梧州 543002; 2. 梧州学院 广西高校图像处理与智能信息系统重点实验室, 广西 梧州 543002;3. 梧州学院 广西高校行业软件技术重点实验室, 广西 梧州 543002; 4. 梧州职业学院, 广西 梧州 543002)

强链回归点集和非游荡点集是动力系统研究的重点,有关强链回归点集和非游荡点集的研究成果[1-7]非常丰富,例如,文献[1]证明了强链回归点集是闭集,文献[2]给出同胚映射f的强链回归点集对f是强不变的,文献[3]给出移位映射的G-非游荡点集等于自映射f在它的G-非游荡点集上形成的逆极限空间.随着动力系统的不断发展,我们需要在度量G-空间中研究G-强链回点和G-非游荡点集的拓扑特征和结构,通过证明得到如下结果:1)f的G-强链回归点集对拓扑群G是强不变的;2) 映射f的G-非游荡点集是映射f的G-强链回归点集的子集;3) 映射fm的G-强链回归点集是映射f的G-强链回归点集的子集;4) 移位映射σ的G-强链回归点集是自映射f在它的G-强链回归点集上形成的逆极限空间的子集.文献[1-2]给出了有关强链回归点集的结果,我们知道强链回归点一定是G-强链回归点,反之不成立,因此本文所得结果推广了文献[1-2]的结论,并为G-强链回归点和G-非游荡点在其他学科中的应用提供了理论基础.

1 基本概念

定义 1[8]设(X,d)是度量空间,G是拓扑群.若映射φ:G×X→X满足:

1) ∀x∈X,有φ(e,x)=x,其中e为G的单位元;

2) ∀x∈X和∀g1,g2∈G,有

φ(g1,φ(g2,x))=φ(g1g2,x),

则称(X,G,φ)是度量G-空间,简称X是度量G-空间.为了书写方便,通常将φ(g,x)简写为gx.

特别地,若(X,d)是紧致度量空间,则称(X,d)是紧致度量G-空间.

定义 2[9]设(X,d)度量G-空间,f:X→X连续,称f是伪等价映射,如果∀g∈G,∀x∈X,∃h∈G使得f(gx)=hf(x)成立.

定义 3[9]设(X,d)是度量G-空间,f:X→X连续,称f是等价映射,如果∀g∈G,∀x∈X,有f(gx)=gf(x).

定义 5[10]设(X,d)是度量G-空间,f:X→X连续,x∈X,称x是f的G-非游荡点,如果∀U∈Ux,∃n∈N+,∃g∈G使gfn(U)∩U≠∅.f的G-非游荡点集用ΩG(f)表示.

注 1Ux表示x的所有邻域组成的集族.

定义 6[10]设(X,d)是度量G-空间,A⊂X,f:X→X连续,记

GA≡{gx|g∈G,x∈X)}.

若G(A)=A,则称A对G强不变.

定义 8[11]设(X,d)是度量空间,f:X→X连续,x∈X.如果∀ε>0,存在f作用下从x到x的强ε-链,则称x是f的强链回归点.f所有强链回归点组成的集合记为SCR(f).

注 2根据强链回归点的概念,下面给出G-强链回归点的概念.

定义 10设(X,d)是度量G-空间,f:X→X连续,x∈X.如果∀ε>0,存在f作用下从x到x的强(G,ε)-链,则称x是f的G-强链回归点.f所有G-强链回归点组成的集合记为SCRG(f).

2 主要结果

引理 1[10]设(X,d)是紧致度量G-空间,G是紧致的拓扑群,则∀ε>0,∃0<δ<ε,当d(x,y)<δ时,∀g∈G,有d(gx,gy)<ε.

定理 1设(X,d)是紧致度量G-空间,f:X→X连续,则G(SCRG(f))=SCRG(f).

(1)

特别地,

d(g0f(y),y1)<δ,

d(gn-1f(yn-1),y)<δ.

由(1)式知

d(ggn-1f(y

由f伪等价知,∃t∈G使得

f(gy)=tf(y),

因此

g0t1f(gy)=g0f(y).

则

d(g0t-1f(gy),y1)<δ,

故

d(g0t-1f(gy),y1)+

则{gy,y1,y2,…,yn-1,gy}是f作用下的强(G,ε)-链,因此gy∈SCRG(f),故

G(SCRG(f))⊂SCRG(f).

由定义知,SCRG(f)⊂G(SCRG(f)),因此

G(SCRG(f))=SCRG(f).

定理 2设(X,d)是紧致度量G-空间,f:X→X连续,则ΩG(f)⊂SCRG(f).

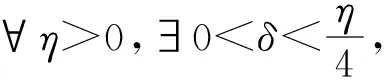
(2)

由z∈ΩG(f)知,∃y∈X,m∈N+和g∈G使得

d(z,y)<δ,

d(gfm(y),z)<δ.

由(2)式知

令xi=fi(y),1≤i≤m-1.x0=xm=z，则有

d(f(y),f(z))+d(gf(x

故{x0,x1,x2,…,xm-1,xm}是强(G,η)-链,则z∈SCRG(f),故ΩG(f)⊂SCRG(f).

定理 3设(X,d)是紧致度量G-空间,f:X→X连续,m≥2,则

SCRG(fm)⊂SCRG(f).

令

xpm+i=fi(yp),

0≤p≤k-1, 0≤i≤m-1,

xkm=y,

易知x0=xkm=y,取

tim-1=gi-1, 1≤i≤k.

于是ti=e,0≤i

注 3由于SCRG(f)对连续映射f不变,因此可以考虑f限制在SCRG(f)形成的逆极限空间,可以得到如下结论.

定理 4设(X,d)是紧致度量G-空间,f:X→X连续,则

SCR

又

故

则

因此

3 结束语

致谢梧州学院校级重点项目(2020B007)对本文给予了资助，谨致谢意.