基于STAR CCM+的离心式冷却水泵叶轮优化设计

雷刚，徐雪汉，谭巍，杨联林，王虎银

(重庆理工大学车辆工程学院, 重庆 400054)

随着汽车电子技术的发展，离心式电子冷却水泵作为冷却系统核心部件之一为汽车动力系统提供源源不断的冷却液，从而防止发动机因工作温度过高而导致功率降低及油耗增大.因此，冷却水泵的性能对发动机的燃油经济性具有重要影响.

汽车冷却水泵的过流部件主要包括叶轮和蜗壳，而叶轮是最核心的过流部件，其结构参数对水泵的性能具有决定性作用.李振兴等[1]应用CAD/CAM技术设计并加工了一种渐开线水泵叶轮，这种参数化建模方法提高了叶轮设计效率；吴杰等[2]提出了一种半闭式摆线叶轮设计方法，结合数值模拟和试验对比分析了优化叶轮和原叶轮的性能.在离心式水泵优化方面，何希杰等[3]基于遗传算法，对离心泵进行优化设计，建立了以离心泵效率最高、汽蚀余量最小为目标函数的数学模型.王幼民等[4]通过建立不同的目标函数，采用遗传算法对离心泵特性进行优化，对比表明优化后的水泵性能有了明显改善.以上对水泵叶轮的设计研究中，由于缺少明确的水泵叶轮结构尺寸及优化方案，使得仿真与试验次数较大，从而增大了研究难度.

为提高汽车冷却水泵叶轮的设计精度，减小数值计算及试验的工作量，文中针对冷却水泵在某一额定运转工况下设计一种半开式叶轮，基于MATLAB遗传算法工具箱[5-7]建立叶轮的数学模型，通过计算得到一组叶轮结构参数的最优组合，从而提高额定工况下水泵的效率.

1 水泵叶轮设计

1.1 叶轮设计理论

半开式叶轮具有结构简单、效率高等优点，在电子水泵中广泛使用[8-9].半开式叶轮主要包括3个部分，分别为叶片、安放叶片的后盖板和位于盖板中间用于连接泵轴的轮毂.叶轮设计集中在叶片，根据离心泵叶轮叶片设计理论[10]，液体在叶轮内的流动可以简化为在若干个流面上的流动，假设液体在每个流面上流动相同且速度均匀分布，因此可以求出液体质点的运动轨迹，然后将轨迹拟合，便可以得到叶片型线方程，即

(1)

在叶轮出口处采用一段圆弧修型，以防止液体回流，叶轮出口处叶片型线方程为

(2)

上述式中：A，B为影响型线长度的系数；a1，b1为影响出口边圆弧处弯曲程度的系数；a2，b2，c为影响进口边叶片弯曲程度的系数.

1.2 叶轮设计

叶片数直接影响液体在叶轮中的流动情况，考虑减少叶片的排挤和表面摩擦，以及使流道内流体有较为均匀的流速，文中设计叶轮叶片数为Z=6.在满足叶片强度要求下，根据设计经验[10],取叶片厚度为1.0 mm.

设计的叶轮需满足水泵的工况要求，参考同类型水泵，确定文中汽车冷却水泵在额定工况下的设计性能参数分别为转速n=3 000 r/min，流量Q=90 L/min，扬程H=4 m，比转数ns=150，水温为70～80 ℃；叶轮主要几何参数包括进出口宽度b1，b2,进出口直径D1，D2,叶片进出口安放角β1，β2.根据相似换算法[11]，确定叶轮的主要几何参数分别为b1=7 mm，b2=5 mm，D1=10 mm，D2=43 mm，β1=67°，β2=48°.

1.3 叶轮及泵壳建模

采用CATIA V5软件进行叶轮三维造型，如图1a所示.泵壳的设计除了考虑叶轮的尺寸之外，还要考虑水泵在汽车上的安装位置和空间布局等因素，文中设计的泵壳如图1b所示.根据经验，泵壳厚度不小于3 mm, 考虑强度因素，这里壳体厚度取3 mm，进口直径8 mm，出口直径7 mm.

图1 水泵三维造型Fig.1 3D model of cooling water pump

泵汽蚀时产生的振动较大，严重时可使过流部件被损坏.对于小流量水泵而言，提高其抗汽蚀性能不容忽视.研究表明，在泵入口处增加导流装置可改善泵的抗汽蚀性能[12]，因此文中在设计时增加了一块导流板.

2 数值模拟

应用计算流体动力学软件STAR CCM+对过流部件流体区域进行数值计算，计算步骤主要包括三维模型流道抽取、网格划分、边界条件设定、求解设置等.

2.1 控制方程及湍流模型

为准确地描述流体的运动，选取N-S方程作为流场求解控制方程[13]，即

(3)

式中：ρ为流体密度；ui，uj为流场中各坐标轴方向平均速度；p为压力；xi，xj为位移；μ为黏性系数；Rij为雷诺应力张量分量.

由于泵内流场为非定常流动，因此选用鲁棒性强且计算精度较高的标准k-ε双方程模型[13]为湍流模型，其输运方程为

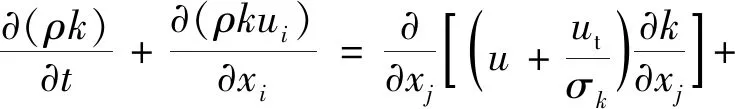
(4)

(5)

式中：σk，σε分别为湍动能k和湍动能耗散率ε相对应的Prandtl数，文中σk=1.0，σε=1.3；Gk为由层流梯度产生的湍流动能；Gb为由浮力产生的湍流动能；YM为可压缩流动的波动；Sk，Sε为用户定义源项；C1ε，C2ε，C3ε及其他参数为经验常数.

2.2 流道抽取及网格划分

对装配体进行流道抽取，并导入STAR CCM+中进行网格划分.网格划分前先进行网格无关性检验，选取网格数N分别为2.72×105，4.56×105，9.85×105，表1为额定工况下水泵性能计算结果.表中H，P，η分别为计算扬程、计算轴功率和计算效率.

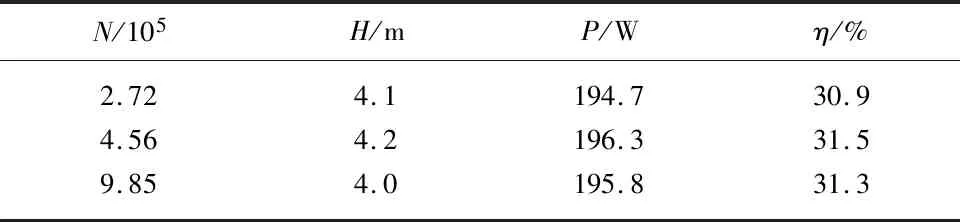
表1 网格无关性计算结果Tab.1 Grid independence results

由表1可以看出，网格数量对计算结果影响不大，具有无关性，因此最终选取N=4.56×105作为计算网格.模型采用四面体网格划分,叶轮部分进行局部加密，划分后的网格模型如图2所示.

图2 泵水体网格Fig.2 Mesh of computational domains

2.3 STAR CCM+分析

首先在STAR CCM+软件中建立旋转坐标系，转速设置为3 000 r/min.采用质量流量入口边界条件，qm=1.5 kg/s，冷却液温度设为80 ℃.设置压力出口，根据水泵性能要求，扬程为4 m(即压力为40 kPa)，则出口压力设置为40 000 Pa，其余参数保持默认.叶轮壁面采用平滑规格，剪应力指定为无滑移，水泵内部流体表面区域采用同样设置.

设AMG线性求解器中约束容差为0.9，收敛容差为0.5，最大迭代步数为8 000，其余参数保持默认.点击视图上方RUN按钮，即可进行迭代计算，并进行后处理.

3 后处理

3.1 水泵流道结果分析

数值计算结束后，在靠近旋转轴端点附近选取截面，得到转速3 000 r/min，流量1.5 kg/s时水泵该截面的绝对压力分布云图、相对速度矢量图以及湍动能分布图，如图3—5所示.

图3 水泵截面绝对压力分布云图Fig.3 Absolute pressure cloud diagram of pump section

由图3可以看出，叶轮的低压区主要集中在叶片中部和叶片的背压面，这是由于叶片在旋转时，叶片背面与液体形成流动分离.叶片旋转带动正面液体旋转，使得高压部分集中在叶片承压面，泵内腔其他区域压力分布较为均匀.

由图4可以看出，腔体内部速度较为均匀，为3.00 m/s左右，速度最大区域集中在出口管上方，最大值达到5.993 m/s.这是因为冷却液在离心力作用下获得较高速度被甩出腔体进入出口管.

图4 水泵截面相对速度矢量图Fig.4 Diagram of relative velocity vector in pump section

由图5可以看出，在该转速及流量下，湍动能值并不大且分布均匀，总体上，湍流脉动程度较小，内部流动相对稳定，水力损失较小.

图5 水泵截面湍动能分布图Fig.5 Diagram of turbulent kinetic energy distribu-tion in pump section

3.2 水泵外特性计算

通过STAR CCM+后处理计算得到冷却水泵在转速3 000 r/min，质量流量1.5 kg/s工况下的外特性参数，为后面叶轮尺寸优化建立初始计算模型参数.水泵外特性参数主要包括水泵扬程(H)、效率(η)以及轴功率(P)，其计算公式分别为

(6)

(7)

(8)

以上式中：pin，pout分别为水泵进口、出口压力；ρ为冷却液的密度；Δh为进口、出口端面高度差；g为重力加速度；T为冷却水泵转矩，数值由STAR CCM+后处理计算得到.

在额定工况下，对水泵流场进行数值计算，得到水泵外特性参数分别为H=4.2 m，P=196.3 W，η=31.5%.

4 基于MATLAB遗传算法工具箱优化

为避免以单一能量损失为目标优化时的缺陷，基于MATLAB遗传算法工具箱，以泵的总能量损失最小为优化目标，通过建立目标函数[14]、优化变量以及约束条件，寻求叶轮结构参数的最优组合，本次优化以水泵额定工况下的外特性参数为例.

对模型实施哈维检验，收尾概率=0.030 7，小于显著性水平5%，所以拒绝原假设，残差存在异方差性。为了处理模型的异方差性，根据残差随着GDP的变化而增大的特点，用GDP^1.5定义权数，修正后的模型即碳排放数量、地区生产总值和碳交易金额的关系可用以下公式表示：

4.1 目标函数确定

泵的总能量损失包括机械损失、水力损失、容积损失，即

P=Pm+PV+Ph，

(9)

式中：Pm为机械损失；PV为容积损失；Ph为水力损失.

机械损失为

(10)

式中：u2为叶轮出口圆周速度；ηm为机械效率.

容积损失为

PV=ρgqHth，

(11)

(12)

式中：Hth为理论扬程；q为叶轮进口密封处泄漏量；φ2为出口滑移系数，φ2=0.85.

水力损失为

Ph=ρgQ(Hth-H).

(13)

F(X)=min(Pm+PV+Ph).

(14)

4.2 优化变量确定

选取对离心式水泵叶轮设计影响较大的参数作为优化变量，分别为进出口宽度b1和b2，进出口直径D1和D2以及进出口角度β1和β2，其他参数可以通过查阅相关资料获取.优化变量可以表示为

X=(b1,b2,D1,D2,β1,β2).

(15)

4.3 约束条件

根据速度系数法和相关模型泵的设计数据[11]，确定文中优化变量的约束条件为

(16)

式中：Km1为叶轮进口轴面速度系数，Km1=0.255.

将额定工况下水泵的设计性能参数代入式(16)，得到各优化变量的取值范围为

(17)

4.4 结果分析

MATLAB遗传算法工具箱GUI因其交互式操作界面而极大简化了使用流程.算法采用实数编码，种群规模G为100，维数为6，通过调用工具箱内相应函数并设置相关参数，经仿真计算得到函数F(X)最佳解的变化和平均值的变化曲线如图6所示.

图6 函数F(X)最佳解的变化和平均值的变化曲线Fig.6 Variation curves of optimal solution and mean of function F(X)

计算得到最后一代的最优解为F(X)=4 535 600,种群平均值MeanF(X)=5 438 771,获得最优解时6个优化变量取值分别为

X=[0.005 8,0.006 2,0.009,0.041,72.4,42].

(18)

表2为优化前后叶轮几何参数对比.

表2 优化前后叶轮结构参数对比Tab.2 Comparison of impeller structural para-meters before and after optimization

为更直观地了解优化后冷却水泵的性能，对表2优化后的冷却水泵再次进行数值计算，得到水泵转速为3 000 r/min时不同运行工况下的水泵外特性参数，并分别绘制叶轮优化前后的扬程、轴功率和效率曲线进行对比，如图7所示.

图7 优化前后水泵外特性曲线对比Fig.7 Comparison of characteristic curves of cooling water pump before and after optimization

由图7a可以看出，优化后水泵的扬程整体有了一定的提升但幅度不大，在流量50 L/min处，扬程达到最高，为4.92 m.随着流量的增大，水泵的扬程逐渐下降.在额定工况下，扬程为4.65 m，满足设计要求性能.

由图7b可以看出，随着流量的增大，水泵的轴功率逐渐增大，优化后水泵轴功率相比优化前降低34%以上，在一定程度上减轻了过载现象.

由图7c可以看出，优化后水泵效率先增大后减小，在流量90 L/min处，即额定工况处水泵效率达到最高为33.8%，相比优化前提高了2.3%.

综上所述，优化后水泵在性能上有所提升，MATLAB遗传算法在对水泵的优化过程中具有重要的作用.

5 结 论

1) 针对水泵某一额定运转工况下对叶轮进行设计，明确了设计目标.通过对水泵的总的能量损失建立目标函数，避免了以单一能量损失为优化目标时的缺陷.

2) MATLAB遗传算法工具箱在寻找叶轮结构参数最优组合时具有明显优越性，且结果合理可靠，通过直接调用工具箱内部函数和遗传算法主程序节省了大量的编程工作.经叶轮优化后的水泵性能优良，额定工况下水泵效率提高了2.3%.