一种数据缺失时的卫星钟稳定度计算策略及对BDS-3评估

王宇谱，赵营营，王 威，李林阳，许普润，马保印

（1. 北京卫星导航中心，北京 100094；2. 武汉大学卫星导航定位技术研究中心，武汉 430079；3. 信息工程大学地理空间信息学院，郑州 450001）

目前，全球卫星导航系统（Global Navigation Satellite Systems, GNSS）已在多个领域得到了广泛应用，地位和作用日益突出[1]。卫星钟作为GNSS星上时间基准和卫星有效载荷的核心组成部分，其性能直接影响着系统服务质量[2]。因此，评估和分析GNSS在轨卫星钟的性能对于系统的运维和服务具有非常重要的实际意义，并且国内外学者对此进行了大量研究[3-7]。而在卫星钟的性能评估和分析中，频率稳定性是表征和反映其性能的一项重要指标[8]，因此在所有的原子钟性能评估和分析中都会计算和分析该指标。GNSS主要基于地面观测和解算得到的卫星钟差数据来计算和分析在轨卫星钟的频率稳定性。在导航卫星的实际运行过程中，由于通信中断、卫星有效载荷故障、观测数据异常等原因经常会造成所获取的卫星钟差数据存在间断、不连续的情况。但是，目前在计算卫星钟的频率稳定度时，缺少较为全面系统的关于数据缺失条件下通过内插补齐方式获取的稳定度结果与基于实际连续完整数据得到相应结果的差异分析及其对应的策略建议等，导致经常会出现同一卫星钟相同时间段的不同稳定度结果，对卫星导航系统的相关研究和运行维护带来了诸多不便。此外，已有的关于GNSS卫星钟频率稳定性评估和分析的相关研究大多是针对GPS系统[9]和北斗二号卫星导航系统（BDS-2）[10]，即使有一些关于北斗三号卫星导航系统（BDS-3）的[11~13]，其也主要是针对试验星[11]和运行时间相对较短的卫星[12,13]，缺少针对运行状态相对稳定后的BDS-3卫星钟频率稳定性较为全面科学的评估和分析。基于此，本文首先分析了卫星钟差数据存在缺失的情况下不同内插补齐数据量对频率稳定度计算结果的影响，同时给出了一种对应的数据缺失条件下的卫星钟频率稳定度计算策略；最后将本文所提的处理策略应用于BDS-3卫星钟频率稳定性分析中，更为客观准确地评估当前已经运行了相对较长时间、卫星钟处于相对稳定状态的MEO卫星的卫星钟的频率稳定度，得到了一些具有较好参考价值的结论。

1 卫星钟稳定度计算方法

在进行频率稳定性分析之前，首先要进行相位频率数据转换、粗差等异常值的处理等，然后计算稳定度值。本文的理论算法涉及有相频数据转换、基于改进中位数（MAD）方法的钟差数据预处理、基于重叠Hadamard方差的频率稳定度计算。

1.1 钟差数据与对应频率数据的转换方法

GNSS卫星钟的钟差（相位）数据转换为对应频率数据的关系式为[9]：

式中，xi为第i历元的钟差值，τ0为第i历元和i-1历元间的时间间隔，对于给定的钟差数据序列，τ0为已知的常数；yi为采样时间间隔为τ0的第i历元的频率值。根据式(1)可以看出，频率数据相对于相位数据其有效位数减少并且数据的数值也变小，这样便于异常值的识别；同时，异常的钟差数据对应于频率数据的峰值，而峰值较易进行探测。因此，钟差数据的异常值识别一般是在其对应的频率数据上进行的。

1.2 基于改进MAD方法的预处理方法

结合1.1节可知，钟差数据的粗差探测一般是在其对应的频率数据上进行的，而频率数据预处理中最常用的方法是中位数（Median Absolute Deviation,MAD）方法，其粗差探测的思路是[10]：将每一个频率数据iy与频率数据序列的中数（MED）加上中位数（MAD）的若干倍之和相比较，即当观测量

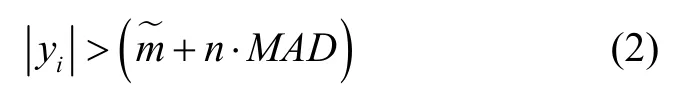
就认为数据yi是粗差点，式中整数n表示倍数，其值根据具体情况需要确定，本文取n=3。在异常值探测出之后，为了避免引入新的数据而造成原始数据一定程度上的失真，本文在探测出异常频率数据后直接将其对应的卫星钟差数据设为空，即这些历元时刻的卫星钟差数据缺失[14]。

1.3 重叠Hadamard方差计算方法

GNSS星载铷原子钟在运行过程中存在较为显著的频率漂移，一般基于Hadamard系列方差能够较为科学合理地进行各类型卫星钟的频率稳定度计算[11]。其中，重叠Hadamard方差具有较高的置信区间且公式相对简单，因此本文使用该方差计算卫星钟的频率稳定度。

基于频率数据的重叠Hadamard方差计算公式为[9]：

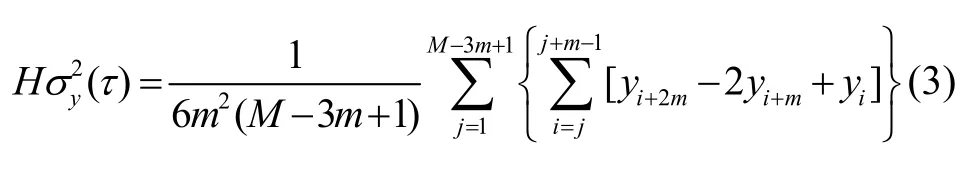
式中，τ = mτ0为平滑时间，τ0为相邻频率数据的采样间隔，yi为频率数据，M为频率数据的个数；m为平滑因子，一般取1≤m≤int(M/3)。

2 数据缺失条件下的频率稳定度计算策略

在卫星钟差（相位）数据的获取过程中，因为通信中断、卫星有效载荷故障、解算策略等多种因素的综合影响，导致最终的数据结果中存在一定的中断或缺失。图1给出了BDS-2卫星导航系统C02卫星的相位数据及其转换得到的频率数据，该钟差数据来自IGS MGEX武汉大学GNSS中心提供的精密星历星载卫星钟差（ftp://igs.gnsswhu.cn/pub/gps/ products），数据的采样间隔为15分钟，数据收集的时间段为2013年1月1日到2013年12月31日共1年。从图中可以看出，该卫星的钟差数据存在多处不连续的间断和缺失。

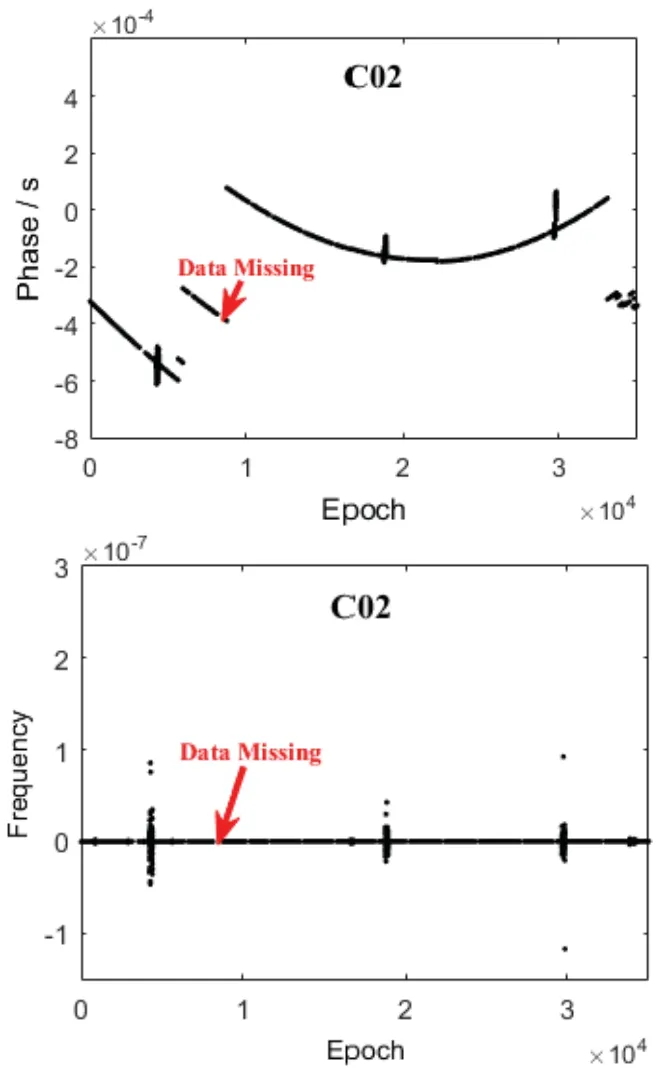
图1 C02卫星的相位数据及其对应的频率数据Fig.1 Phase data of C02 satellite and its corresponding frequency data

而在实际基于卫星钟差数据计算频率稳定度时，比较理想的条件是数据连续均匀且不存在较多的异常点；如果所使用数据存在缺失不完整的情况时，通常是需要通过数据内插等方式将其补充完整。但是，目前在计算卫星钟的频率稳定度时，缺少较为全面系统的关于数据缺失条件下通过内插补齐方式获得的稳定度结果与基于实际连续完整数据得到的稳定度结果的差异分析及其对应的策略建议等。因此，本节分析了不同内插补齐数据量对频率稳定度计算结果的影响，得到了一些可供参考的新结论，同时给出了一种数据缺失条件下的卫星钟频率稳定度计算策略。

本节以BDS-3的两颗MEO卫星C27和C36为例进行分析，其中前者搭载的是被动型氢原子钟（PHM），后者搭载的是铷原子钟（RAFS）[13,16,17]。考虑到天稳定度（简称天稳）是衡量原子钟频率稳定性的重要指标，这里主要以天稳结果作为分析对象。同时在计算天稳时，需要至少15天的数据才能得到可靠的结果[15]，因此图2-3给出了两颗卫星15天的钟差数据及其转换得到的频率数据。

图2 C27卫星的钟差数据及其对应的频率数据Fig.2 Clock bias data of C27 satellite and its corresponding frequency data

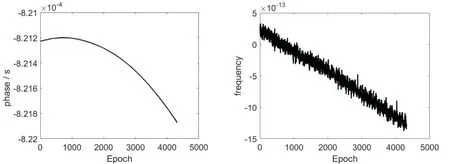
图3 C36卫星的钟差数据及其对应的频率数据Fig.3 Clock bias data of C36 satellite and its corresponding frequency data

该钟差数据来自IGS MGEX德国地学中心（GFZ）提供的精密卫星钟差（ftp://ftp.gfz- potsdam.de/GNSS/products/ mgex/），数据的采样间隔为5分钟，数据收集的时间段为2020年3月28日到2020年4月11日共15天。从图中可以看出这些数据的变化连续平稳，并且数据完整不存在缺失，适合作为实验数据。需要说明的是使用15天的数据与使用30天的数据或者其他更长时间段的数据，所得到的结论类似。

为了获得较为可靠的稳定度计算结果，同时为了便于对比分析不同时间段稳定度的变化情况，在基于长时间段（多于15天）卫星钟差数据计算卫星钟天稳时，本文采取的策略是：根据通常认为“当误差小于正常值的1/3时，该项误差影响被认为可以忽略”的原则，当所使用时段的钟差数据缺失率低于该数据段数据总量的4%时（以数据长度为15天、数据采样率为5分钟的一段卫星钟差数据为例，正常情况包含了288历元/天×15天=4320历元，当一个时间段的钟差总数多于4104个的时候），通过该数据段钟差数据所对应的频率数据拟合一次多项式模型（其他拟合模型亦可，结果的差别可忽略）来补充缺失历元的数据，然后基于补充后的连续完整数据计算该时间段的频率稳定度结果；否则，不计算该时间段的稳定度结果，因为此时数据缺失相对较多，通过内插补齐之后的数据序列计算的稳定度结果将会与实际数据计算的结果存在较大偏差（具体分析见下文），不能相对准确客观地反映真实的卫星钟稳定度特性，除非是有其他的特殊要求等。

同时，在计算稳定度结果之前，首先分析本文稳定度计算策略中数据缺失情况对计算结果的影响情况。以15天的数据缺失5%（216个数据）为例，缺失数据出现在整个数据段的不同位置，对稳定度计算结果的影响不一样：当其分散于整个数据段时，基于一次多项式补充时可以看作是一般的数据插值问题，并且是根据较多的数据插值相对较少的数据，此时能够得到较高精度的数据补充结果，其对频率稳定度计算结果的影响也相对小；而当216个缺失数据集中在一起时，特别是其位于整个数据段的最后或者起始位置时，此时补充这些缺失的数据相当于通过已有的数据对其进行预报，而通常在相同数据条件下数据内插的精度要高于数据（外推）预报的精度，此时得到的数据补充结果精度相对较差，对稳定度计算结果的影响也最大。因此，这里分析对稳定度计算结果影响最大的数据缺失情况，即缺失数据集中在整个数据段的尾端时的情况（起始位置类似）；图4和图5分别给出了模拟两颗卫星的数据缺失率从1%（Value1）到25%（Value25）变化时，基于本文所提的数据拟合补齐策略计算得到的频率稳定度（平滑时间在一天以内）结果和真实数据计算的频率稳定度结果的差值绝对值变化情况。

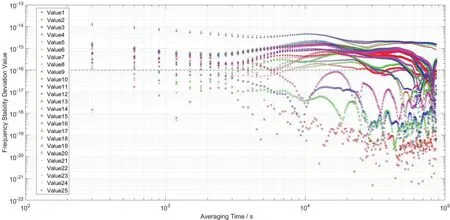
图4 C27卫星在不同数据缺失率条件下的稳定度偏差图Fig.4 Stability deviation diagram of satellite C27 under different data missing rates

图5 C36卫星在不同数据缺失率条件下的稳定度偏差图Fig.5 Stability deviation diagram of C satellite 36 under different data missing rates

从图4-5可以看出，两颗卫星均出现随着数据缺失率的增加其稳定度偏差值变大的情况，同时基于内插补齐数据计算的稳定度结果与基于真实数据计算的稳定度结果差异也在变大。此外，拟合数据的多少及其出现位置的不同，使得稳定度曲线图所表现出来的噪声特性不一样，导致实际噪声失真。

另外，考虑到目前BDS-3的MEO卫星钟天稳基本保持在10-15量级（详见下一节计算结果），因此为了确保内插补齐数据计算结果的可靠性，需要保证其结果与真实数据计算结果的差值比真实天稳结果低一个数量级，即差异控制在10-16量级。基于此，根据图中结果可知需将数据缺失率控制在4%左右。为了进行详细的定量分析，表1给出了这两颗卫星的真实天稳及其与不同数据缺失率（10%以内）条件下的天稳的差值绝对值。

从表1的结果可知，不论是被动型氢钟还是铷钟，两个卫星钟的真实天稳值基本相当，但是相同的数据缺失率对基于拟合补齐后的数据计算的稳定度结果却存在较为明显的差异，这说明相同的数据缺失率对于不同卫星钟频率稳定度计算结果的影响是不同的。同时可知，当数据缺失率小于10%时，两种稳定度结果的最大偏差基本能够保持在比实际天稳小一个数量级的10-16，该条件下基于内插补齐数据计算的结果基本可用，但是为了确保稳定度结果的客观准确需要进一步细化对缺失率的限制；根据通常认为的“误差小于正常值1/3时，该项误差影响被认为可以忽略”的原则，考虑计算的天稳在10-15量级而其1/3对应的值约为3.33×10-16，而从表1中可以看出，当C27的最大偏差值为3.46×10-16时对应的缺失率为4%、C36的最大偏差值为3.42×10-16时对应的缺失率也是4%，因此综合考虑后本文所提策略要求数据缺失率不高于4%才能得到相对客观准确的稳定度结果。

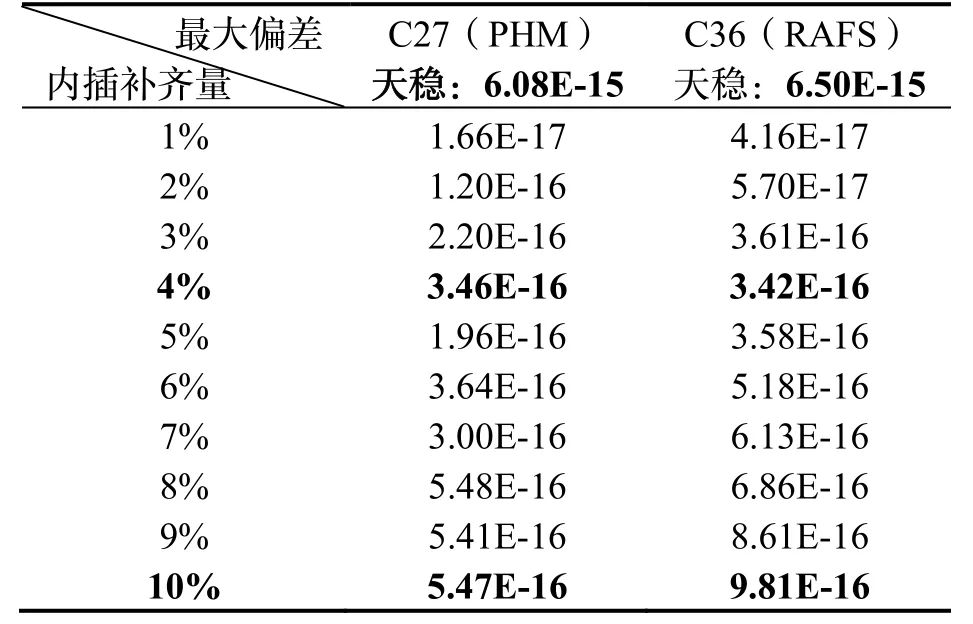
表1 两颗卫星不同数据缺失率条件下的天稳差值绝对值Tab.1 Absolute values of the daily stability differences of the two satellites under different data missing rates

最后，基于上述分析，再次明确本文所提策略可以归纳为：基于较长时间段（时长大于15天）的卫星钟差数据进行卫星钟的频率稳定性分析时，当所使用时段的钟差数据缺失率低于该数据段数据总量的4%时，通过该数据段钟差数据所对应的频率数据拟合一次多项式模型来补充缺失历元的数据，然后基于补充后的连续完整数据计算该时间段的频率稳定度结果；否则，不使用该数据进行频率稳定度结果的计算和分析。

3 BDS-3卫星钟频率稳定性分析

将本文所提的处理策略应用于BDS-3卫星钟频率稳定性分析中，更为客观准确地评估当前已经运行了相对较长时间、卫星钟处于相对稳定状态的MEO卫星的卫星钟频率稳定度。表2给出BDS-3卫星及其卫星钟的相关信息，其中加粗内容为本文所选取进行频率稳定度分析的卫星及其信息。此处所使用的卫星钟差数据的来源与前文C27和C36一样，只是为了更为充分的进行频率稳定性分析，此处所用数据的时间段为2020年3月28日到2020年5月23日共57天，同样的数据采样间隔为5分钟。

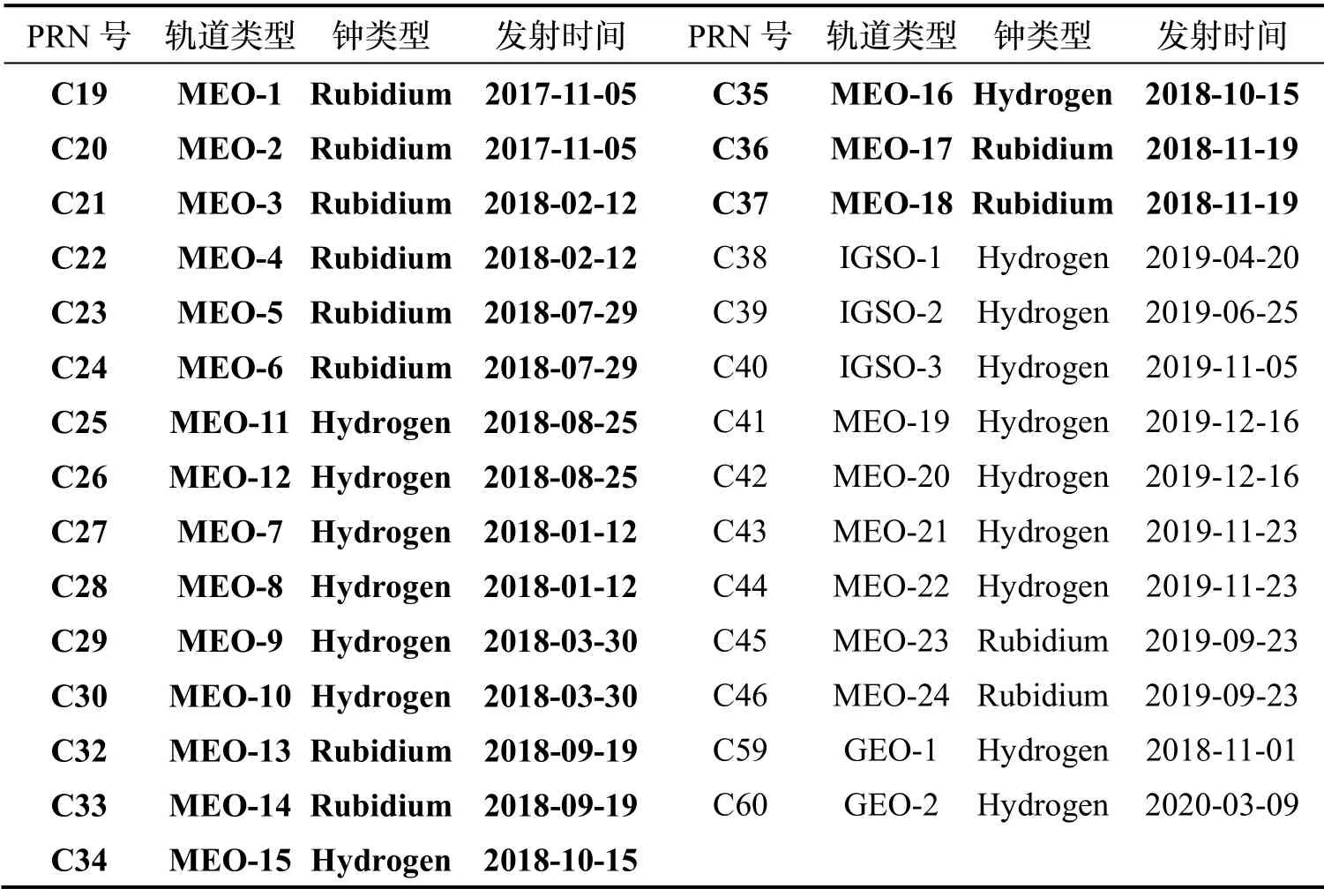
表2 BDS-3卫星及其卫星钟的相关信息[16,17]Tab.2 The relevant information of BDS-3 satellite and its onboard atomic clock[16,17]

图6 -7按照卫星钟类型分别给出了稳定度计算结果的曲线（Sigma-Tau曲线图），并且图示中给出了各卫星钟的天稳结果。对比图6-7的结果可以看出，BDS-3各卫星的星载氢钟较星载铷钟的频率稳定度变化波动相对要小，特别是平滑时间超过万秒之后表现得更为显著；这是因为星载铷钟存在较为显著的频率漂移，随着取样时间的增加，其性能较氢钟将会出现较为明显的下降。同时，从图6中可以看出，不同的星载铷钟其频率稳定性存在着较为显著的差异，例如C22卫星钟的天稳比C32卫星钟的天稳差了将近一倍；而从图7可以看出，不同的星载氢钟其性能差异相对较小，各个星载氢钟的性能趋于一致。

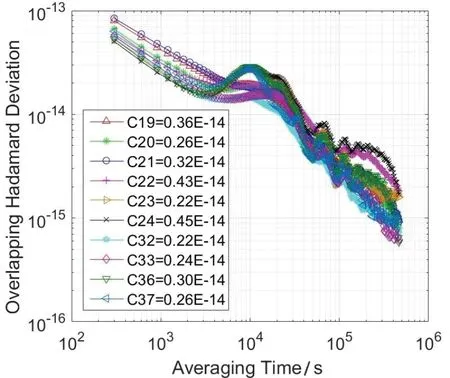
图6 铷钟频率稳定度曲线Fig.6 Frequency stability curve of rubidium clock

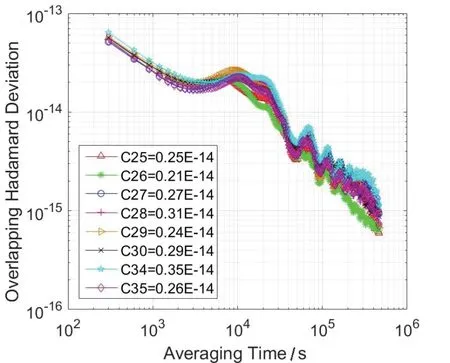
图7 氢钟频率稳定度曲线Fig.7 Frequency stability curve of hydrogen clock

此外，对比两张图还可以看出，万秒稳以内的相对较短时间内的频率稳定性，除了部分星载铷钟的性能与氢钟的性能保持基本一致均相对较好之外，其余铷钟的短期稳定性也相对氢钟要差一些。因此，这在一定程度上说明了BDS-3的星载氢原子钟性能优于其星载铷原子钟的性能。

最后，为了定量对比各卫星钟的频率稳定性并评估BDS-3卫星钟的稳定性，表3给出了各卫星钟的万秒稳和天稳统计结果，同时给出了对应的平均值。从表3可以看出，铷钟的平均万秒稳与氢钟的平均万秒稳基本相当，分别为2.18×10-14和2.23×10-14，这说明在相对较短时间内整体而言BDS-3星载铷钟的性能优于星载氢钟的性能；但是随着时间的增加，由于铷钟较氢钟存在更为显著的频率漂移，导致整体而言氢钟的天稳优于铷钟的天稳，两者的天稳平均值分别为3.10×10-15和2.77×10-15。对比已有关于BDS-2和GPS BLOCK IIF的卫星钟天稳结果[9,10]可知，BDS-3氢钟和铷钟的性能比BDS-2铷钟的性能高出一个数量级，与GPS IIF铷钟的性能处于相同量级但又明显优于其性能。最后，根据BDS-3卫星钟的频率稳定度平均结果可知，其万秒稳和天稳分别为 2.20×10-14和2.96×10-15，该结果表明BDS-3在轨卫星的卫星钟性能在当前所有卫星导航系统中处于先进甚至是领先水平，有效地保证了BDS-3的先进性和高质量的服务水平。

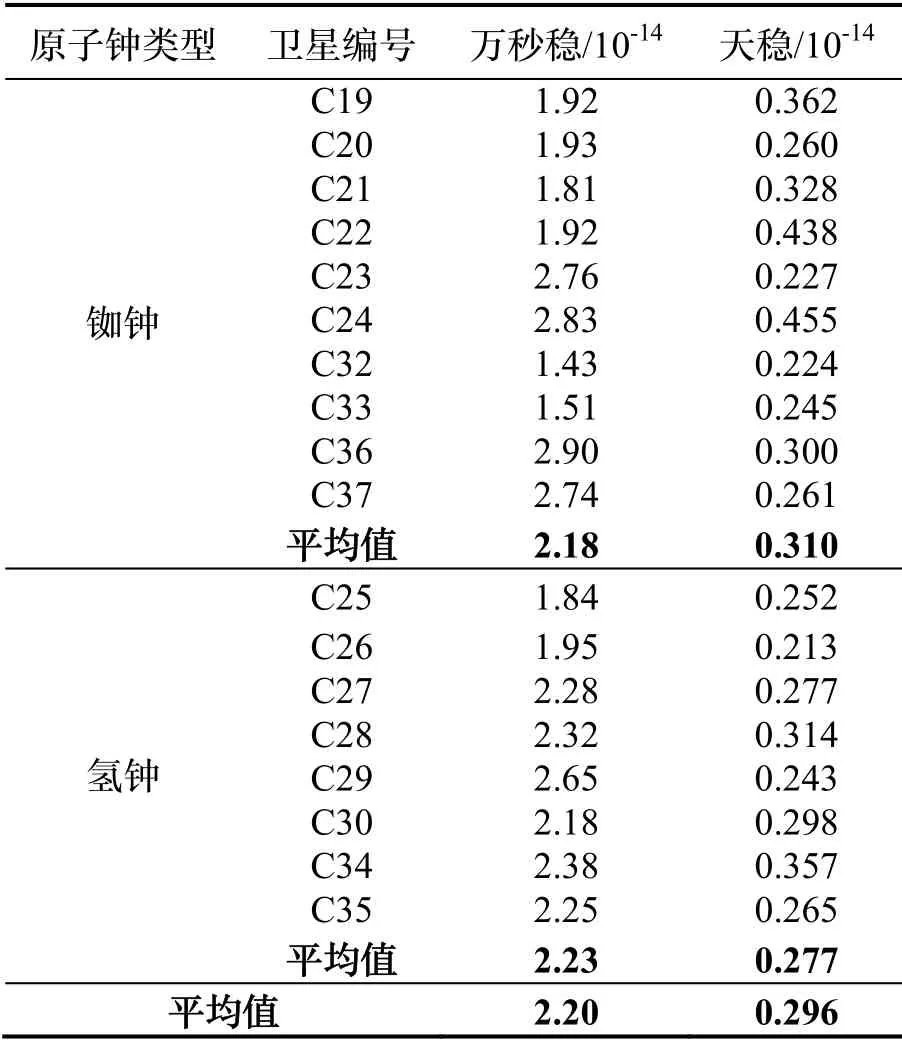
表3 BDS-3卫星钟频率稳定度的统计结果Tab.3 Statistical results of frequency stability of BDS-3 space-borne atomic clocks

4 结 论

GNSS卫星钟的频率稳定性是表征在轨卫星性能的重要指标之一。在基于卫星钟差数据计算并分析频率稳定性的过程中，经常会出现所使用的钟差数据存在缺失不完整的情况。但是目前缺少较为全面系统的关于不同的钟差数据缺失对频率稳定度结果影响的相关分析并且也缺少相应的有效可靠的处理策略。基于此，本文在分析不同数据缺失率对频率稳定度计算结果影响的基础上，提出一种数据缺失条件下的频率稳定度计算策略并将其应用在BDS-3卫星钟性能的评估与分析中，得到了较为可靠准确的评估结果及相关结论：

（1） 基于较长时间段卫星钟差数据进行卫星钟的频率稳定性分析时，当该数据的缺失率低于4%时，可基于内插补充完整后的连续数据计算该时间段的频率稳定度结果；否则，不使用该数据进行频率稳定度结果的计算和分析。

（2）BDS-3铷钟的平均万秒稳和天稳分别为2.18×10-14和3.10×10-15，氢钟的平均万秒稳和天稳分别为2.23×10-14和2.77×10-15；其结果比BDS-2铷钟的性能高出一个数量级，与GPS IIF铷钟的性能处于相同量级但又明显优于其性能。

（3）在相对较短时间内整体而言BDS-3星载铷钟的性能优于星载氢钟的性能，但是随着时间的增加，由于铷钟较氢钟存在更为显著的频率漂移，导致整体而言氢钟的天稳优于铷钟的天稳。

（4） BDS-3在轨卫星的卫星钟性能在当前所有卫星导航系统中处于先进甚至是领先水平，能够有效保证BDS-3的先进性和高质量的服务水平。