基于灰色马尔科夫模型的建筑施工安全事故伤亡预测

陆明刚，周 乾，彭粮波

（吉林建筑大学 应急科学与工程学院，吉林 长春 130118）

1 研究背景

在建筑施工作业中，由于建筑施工行业本身具有的特点，每年都会有大大小小的建筑施工安全事故发生，给人民的生命安全和身心健康带来重大损害，通过对建筑施工安全事故伤亡数进行有效且精准地预测，就可以为建筑施工安全事故预防提出有效的预防措施，提供相应的预防建议，也可以给建筑施工作业人员的生命安全和身心健康提供一定的保障，减少国家和建筑企业的部分经济损失，也能对社会稳定做出一定的贡献，对于个人、社会和国家都具有十分重要的意义。

当前，全球范围内已经研究出了很多种对事故未来发展趋势进行预测的预测法，其中如BP 神经网络法[1]、回归分析法[2]、时间序列预测法[3]、灰色理论预测法[4]和马尔科夫预测法[5]这5 种预测法是比较常见的，但前三种事故预测方法由于自身存在的缺陷不适用于现在研究的建筑施工安全事故的伤亡预测上，而对于灰色理论预测法和马尔科夫预测法而言，前者预测方法主要优点在于不需要大量样本并且样本不需要有规律性的分布，但是这就导致灰色模型预测法只能预测未来数据的变化趋势，不能较精确地预测出波动幅度较大的数据点，而后者马尔科夫预测法的主要特点就是无后效性，即事物出现的状态只与其前一次的状态有关，与其他任意时刻的状态无关。于是笔者结合两种预测模型的优点，从而得到对事故预测效果更佳的灰色马尔科夫模型[6]。

2 模型建立

2.1 灰色GM（1，1）预测模型

灰色预测模型（GREY MODEL）是原始序列生成后建立的微分方程，该模型为一个变量一阶线性动态模型，只需要一个原始序列就可建模，建立模型的过程如下

设参数向量

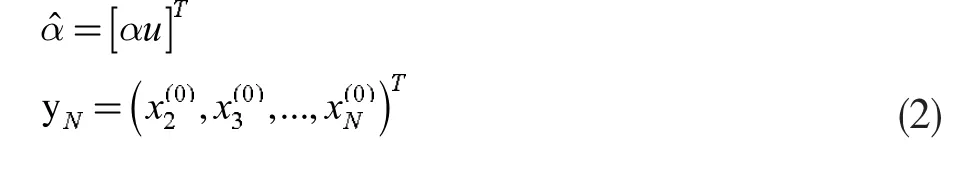
得到响应方程为

建模运算后需作逆生成

预测模型的后验差检验：

后验差检验，记为0 阶残差为

残差均值

残差方差

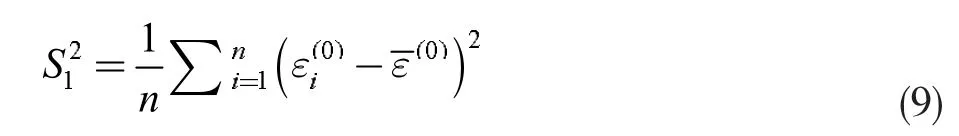
原始数据均值

原始数据方差

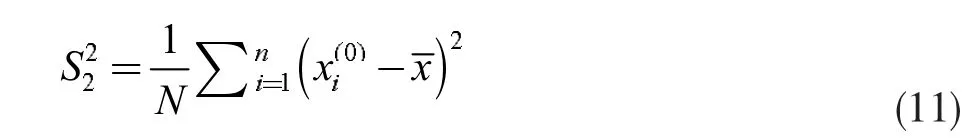
因此，可计算后验差检验指标：

后验差比值c

小误差概率p

计算得出两项指标后，可对比如下四个等级查出精度检验等级：

第一等级：好p>0.95，c＜0.35；第二等级：合格p>0.8，c＜0.5；

第三等级：勉强p>0.7，c＜0.45；第四等级：不合格p≤0.7，c≥0.65。

2.2 灰色马尔科夫模型

2.2.1 状态划分

运用灰色GM（1，1）模型得出的建筑施工事故数或伤亡数的预测值X，将其与实际值x（0）N做差得到残差，用残差除以真实值得到的相对误差为基准，划分3～5 个状态区间。Ei=[φ1，φ2]，其中Ei为系统处于第i 种状态，φ1,φ2分别是状态区间的上下限。

2.2.2 状态转移概率

式中，Eij为状态i 到j 的一步转移次数，Ei为i 状态的数量。由于序列最后的状态转向不明确，故计算pij（k）时要去掉数据序列中最末尾的那个Ei。

从而得到N×N 阶的状态转移矩阵

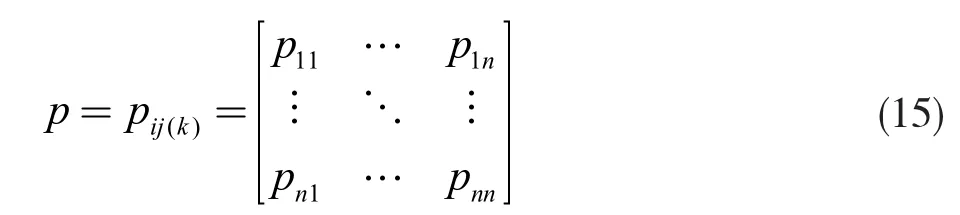
式中：p11是指数据从状态1 一步转移到状态1 的概率。

2.2.3 预测值的计算

式中，X（0）为灰色模型预测值，φ1n，φ2n为状态区间的边界值，当状态处于高估时取正，低估时取负。

3 模型在建筑施工安全事故中的应用

灰色GM（1，1）模型预测结果：

以浙江省某市2010-2021 年发生的建筑施工安全事故的伤亡人数为基础，对数据进行一系列处理，建立灰色预测模型GM（1，1），对模型进行求解并预测未来事故的趋势。该市2010-2021 年建筑施工安全事故的伤亡人数见表1。

3.1 原始数据处理

利用公式(1)～(6)，由表1 确定原始序列为

表1 各年伤亡人数的灰色预测值、残差、相对误差和状态

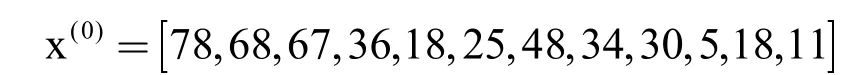
累加生成新序列为

求GM（1，1）的灰色参数a 和u

得伤亡人数的模型

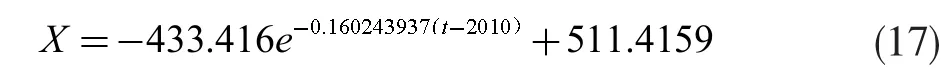
用式(7)～(13)对预测模型进行精度检验，得到p=0.833，c=0.495。

对照精度检验等级，得该市建筑施工安全事故的伤亡人数采用GM（1，1）模型的精度为第二等级“合格”，应用预测该市建筑施工安全事故的变化趋势是合理的，预测值与实际值较为接近，基本满足精度需求。

根据所建立的灰色GM（1，1）模型得到该市未来几年的建筑施工安全事故的伤亡人数及残差和相对误差，所得数据见表1。

3.2 马尔科夫修正预测值

根据表1 中误差结果显示，建筑施工安全事故的伤亡数的灰色预测值与实际值的相对误差范围为（-0.719224，0.66667933），由此可将各年伤亡数发生状态划分为3 种：E1（-0.719224，-0.25726），E2（0.25726，0.204714），E3（0.204712，0.66667933），得 到2010～2021年建筑施工安全事故的伤亡数的各年所处状态，见表1 的最后一列。

根据各年所处的状态，可得到一步状态转移矩阵

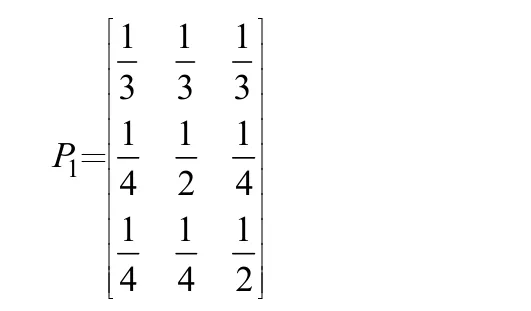
根据转移矩阵，对历年灰色预测值进行修正，并对未来几年的事故伤亡数使用灰色马尔科夫模型进行预测，最终得到的预测值见表2。

表2 建筑施工安全事故伤亡数及预测值

3.3 对比灰色预测值和马尔科夫修正值

见图1，三条折线分别表示了浙江省该市的2010-2021 年的伤亡数，2010-2023 年的灰色预测值和灰色马尔科夫预测值三组数据的变化情况，可以明显的看出，灰色预测值只能预测出浙江省该市的建筑施工安全事故伤亡数总体呈现出下降的趋势，灰色预测值与大部分对应的真实伤亡数之间存在着较大的误差，最大误差达到0.719 224。但通过马尔科夫模型对灰色预测值进行修正后可发现，修正后的灰色马尔科夫预测值在大部分数据点都更能接近真实值，所以也能更好的对未来建筑施工安全事故伤亡数进行预测。因此，采用灰色马尔科夫预测模型可结合两种模型优点，大幅度提高预测精度。

图1 建筑施工安全事故伤亡数预测图

4 结论

（1） 建筑施工安全事故的伤亡数可以采用灰色预测法预测，但其预测结果误差较大，只能反应预测数据的大体发展趋势。

（2） 灰色马尔科夫模型在预测建筑施工安全事故伤亡数上相较于灰色预测模型具有更为精准的预测效果，预测值更能反映出数据具体的变化情况。

（3） 笔者对浙江省某市的建筑施工安全事故的伤亡数进行预测，结果显示未来几年的伤亡人数都是逐年下降的，利用该模型预测该市未来建筑施工安全事故的变化趋势，对该市事故预防具有指导意义。