一类泛函极小值点的几何刻画

薛 荣

(中国人民银行兰州中心支行 国际收支处，甘肃 兰州 730000)

0 引言

变分理论旨在研究泛函的极大值和极小值问题，它的解法非常类似于数学分析中函数的极大值和极小值的方法.变分在泛函的研究中所起的作用，如同微分在函数的研究中所起的作用.这里先对变分的概念作以扼要陈述.

Δf=
f[y(x)+αδy]-f[y(x)]=
L[y，αδy]+β(y，αδy)|α|max|δy|.

f[y+αδy]对α的导函数于α=0时的值等于

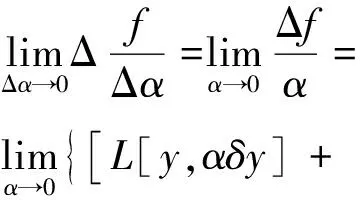
因此

如果Δf=f[y(x)]-f[y0(x)]≤0(≥0)，则说泛函f[y(x)]在y=y0(x)上达到极大值(极小值).如果Δf≤0(≥0)，而只在y=y0(x)时才有Δf=0，则说泛函f[y(x)]在y=y0(x)上达到严格的极大值(极小值)[1-3].

本文就复Hilbert空间中共轭双线性Hermite泛函的极小值和相应的变分不等式作一些讨论.

1 预备知识

(1)φ(αx+βy，z)=αφ(x，z)+βφ(y，z);

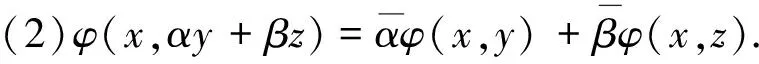
定义2[5]设φ(·，·)是线性空间X上的一个共轭双线性泛函，如果存在M>0，使得

|φ(x，y)|≤M‖x‖‖y‖(∀x，y∈X)，

则称φ(·，·)是X上的有界共轭双线性泛函.当φ(·，·)是X上的有界共轭双线性泛函时，记

称‖φ‖是泛函φ(·，·)的范数.

引理1设φ(·，·)是内积空间X上的共轭双线性泛函，则φ(·，·)是有界的⟺φ(·，·)是二元连续的.

证明设φ(·，·)在X上有界，并设xn，x，yn，y∈X(n=1，2，…)，xn→x，yn→y.由于

|φ(xn，yn)-φ(x，y)|≤
|φ(xn，yn)-φ(xn，y)|+
|φ(xn，y)-φ(x，y)|≤
‖φ‖(‖xn‖‖yn-y‖+
‖xn-x‖‖y‖)→0(n→+∞)，

所以，φ(·，·)是二元连续函数.

反之，设φ(·，·)是二元连续函数，如果φ(·，·)不是有界的，即存在{xn}，{yn}⊂X，‖xn‖=1，‖yn‖=1，使得

|φ(xn，yn)|≥n3(n=1，2，…).

显然

又因为φ(·，·)是双线性泛函，易知φ(0，y)=φ(x，0)=φ(0，0)=0 (∀x，y∈X)，从而由上式得到

这与φ(·，·)是二元连续函数的假设矛盾.所以φ(·，·)是有界的.证毕.

引理2[4-5](变分引理) 设X是Hilbert空间，M是X的一个非空闭凸子集，则∀x∈X，∃|y0∈M，使得

2 主要结果

定理1[6]设X是复Hilbert空间，φ(x，y)是X上的共轭双线性Hermite泛函，并且∃M>0，δ>0，使得

δ‖x‖2≤φ(x，x)≤

M‖x‖2(∀x∈X).

又设u0∈X，E是X中的一个闭凸子集，则函数

x|→φ(x，x)-Re(u0，x) (x∈X)

在E上达到最小值，并且达到最小值的点x0满足变分不等式

Re[2φ(x0，x-x0)-(u0，x-x0)]≥
0 (∀x∈E).

证明(1)先证φ(·，·)是X上的有界共轭双线性泛函，并且‖φ‖≤M.

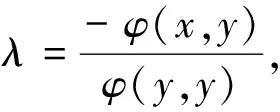
从而

再由题设给出的不等式得，

|φ(x，y)|≤M‖x‖‖y‖(∀x，y∈X).

因此，φ(·，·)是X上的有界共轭双线性泛函，并且‖φ‖≤M.

(2)证明定理1.记f(x)=φ(x，x)-Re(u0，x)(x∈X).根据引理1，φ(·，·)是X上的二元连续线性泛函.又容易验证Re(u0，x)是X上的实值连续线性泛函，所以f(x)是X上的实值连续线性泛函.注意到线性连续和线性有界等价，因此，f(x)在X上有界，从而有下确界.由于E是Hilbert空间X中的闭凸子集，据引理2(变分引理)，∀x∈X，∃|x0∈E，使得

于是

|f(x)-f(x0)|=|f(x-x0)|≤
‖f‖‖x-x0‖=‖f‖ρ(x，E) (∀x∈X).

下证变分不等式.记Δx=x-x0(x，x0∈E).设t∈(0，1)，则x0+tΔx=tx+(1-t)x0∈E，从而

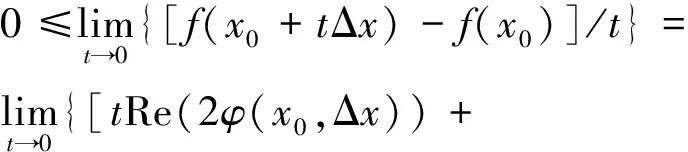
证毕.

定理2设X是复Hilbert空间，ψ是X上的线性连续泛函，M是X中的一个闭凸子集，则∃u0∈X，使得函数

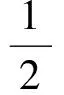
在M上有最小值，并且达到最小值的点x0满足变分不等式

Re[(x0，x-x0)-(u0，x-x0)]≥
0 (∀x∈M).

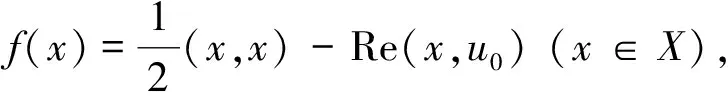
从而

|f(x)-f(x0)|=|f(x-x0)|≤
‖f‖‖x-x0‖=
‖f‖ρ(x，M) (∀x∈X).

下证变分不等式.记Δx=x-x0(x，x0∈M)，并设t∈(0，1)，则x0+tΔx=tx+(1-t)x0∈M，从而

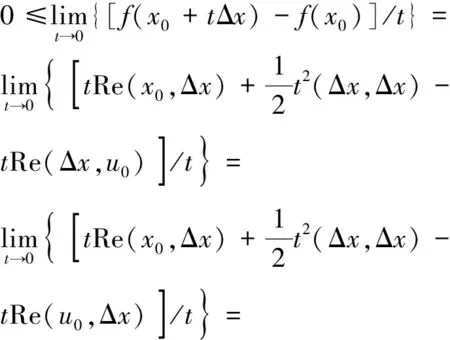
证毕.

定义4设φ(·，·)是线性空间X上的一个共轭双线性泛函，称由

q(x)≜φ(x，x) (∀x∈X)

定义的函数q(x)为X上由φ诱导的二次型.

引理3设φ(·，· )是线性空间X上的共轭双线性泛函，q是由φ诱导的二次型,则

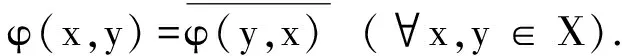
证明“⟸”是显然的.下证“⟹”.由于

从而

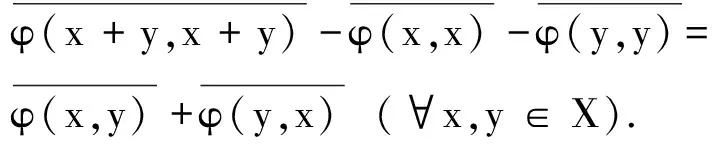
即得

(1)

把式(1)中的y换成iy，

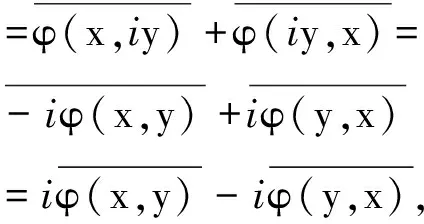
左右两端同除以i,得

(2)

式(1)与式(2)相减,即得

证毕.

定理3设X是复Hilbert空间，A为X的非空闭凸子集，f∈X*，φ(·，·)为X上的有界共轭双线性Hermite泛函,则∃|x0∈A，使得函数

x|→φ(x，x)-Ref(x) (∀x∈X)

在A上达到最小值，并且达到最小值的点x0满足变分不等式

Re[2φ(x0，x-x0)-f(x-x0)]≥
0 (∀x∈A).

证明记ψ(x)=φ(x，x)-Ref(x) (∀x∈X).由题设，φ(·，·)是X上的共轭双线性Hermite泛函，据引理3，φ(x，x)∈R(∀x∈X).又由题设，φ(·，·)在X上是有界的，据引理1，φ(·，·)是X上的二元连续泛函.又据题设，f∈X*，因此，ψ(x)是X上的实值连续线性泛函.由于线性泛函的连续性和有界性等价，所以，ψ(x)在X上有界，从而有下确界.据题设，A是Hilbert空间X中的非空闭凸子集，据引理2 (变分引理)，∀x∈X，∃|x0∈A，使得

于是

|ψ(x)-ψ(x0)|=
|ψ(x-x0)|≤‖ψ‖‖x-x0‖=
‖ψ‖ρ(x，A) (∀x∈X).

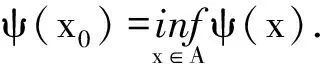
下证变分不等式.记Δx=x-x0(x，x0∈A)，设t∈(0，1)，则x0+tΔx=tx+(1-t)x0∈A，从而

证毕.

3 结语

本文使用初等方法讨论了与复Hilbert空间中范数相关的泛函的极小值的存在性，并对极小子给出了几何刻画.定理1讨论的是一个经典的泛函极小值和与之相关的变分不等式，但笔者没有看见过它的证明，故在此给出了一个较为初等的证明.