基于MOPSO的民航电动特种车辆充电调度策略
高建树,陈 煜,赵志民
(中国民航大学a.机场学院;b.电子信息与自动化学院,天津 300300)
随着中国民航业的迅猛发展,航班数量急速增长,这就要求机场航班地面保障服务有更高的效率。据相关资料[1]显示,地面特种车辆调度失误是航班延误主要原因之一,因此提升特种车辆调度的准确性,减少调度失误是民航特种车辆正常运行的主要任务。而随着中国民用航空局“油改电”项目的实施,中国机场燃油特种车辆将逐步被电动特种车辆替代[2]。电动特种车辆与燃油特种车辆有着明显区别,传统的燃油特种车辆补给一次燃油即可进行多次航班地面保障服务,所以传统的燃油特种车辆无需考虑自身的能源补给。而电动特种车辆受限于电池技术导致充电时间较长和续航能力较差,所以考虑机场电动特种车辆充电时长的特种车辆调度管理成为航班地面保障服务研究的关键问题之一。
目前,国内外对特种车辆的调度研究主要采用单车单航班调度的方式[3-6],此类调度方式可以快速地解决某一种特种车辆的调度问题,但对于整个机场特种车辆的调度效率较低。针对多类型特种车辆的调度,相关学者采用智能算法建立调度模型并进行求解[7-9],但仍存在忽视不同类型特种车辆进行航班保障服务任务之间的时间约束关系的问题。随着机场电动特种车辆增加,部分学者针对电动特种车辆进行了相关研究[10-11],但仅考虑了电动特种车辆的充电问题,没有解决多航班保障任务之间的次序问题,无法体现航班保障服务任务之间严格的次序关系。
目前针对特种车辆的相关研究大多基于单一车型进行调度或针对传统的燃油特种车辆进行研究,由于电动特种车辆自身充电所耗时间远大于传统的燃油特种车辆,所以传统的燃油特种车辆调度策略并不适用于当前应用更为广泛的电动特种车辆的调度。因此,对民航电动特种车辆充电调度的研究,在严格遵守航班保障任务次序关系的前提下,结合磷酸铁锂电池“浅充浅放”模式的实际使用方式,通过对一段时间内航班任务所需服务车辆的耗电情况的整体计算,将航班地面保障服务任务合理分配给机场内的电动特种车辆,使得电动特种车辆可以依据其航班保障任务的耗电量进行准确的充电补给,进而避免了车辆因充电时间过长而过多占用充电桩和因充电时间过短导致车辆频繁充电的情况出现,进而达到提升充电桩的使用效率,降低车辆总体充电时长的目的,最终提升车辆调度的准确性。本文采用多目标粒子群优化(MOPSO,multi-objective particle swarm optimization)算法,运用Matlab 进行编程并求解模型。粒子群优化算法有很多优点,包括目的性强、寻优方向清晰、收敛速度快、与其他算法更容易结合[12],目前该算法在电动车辆有序充电问题[13-14]中运用成熟,本文提到的民航电动特种车辆充电调度也同属于该问题,有一定的延续性。通过对模型求解最终实现了减少特种车辆数量和降低充电时长的目的,可为民航电动特种车辆充电调度问题的研究提供借鉴。
1 民航电动特种车辆充电调度建模
1.1 问题描述
通常在航班离港前,需由多种民航特种车辆来完成排除污水、更换清水、配备餐饮、装载货物、乘客换乘等一系列航班地面保障服务。
以下针对6 种不同类型的电动特种车辆的充电调度管理进行相关研究。给定需要进行航班地面保障服务的飞机数量,以及可进行航班保障服务任务的各种电动特种车辆数量,在航班地面保障服务之前,确定各电动特种车辆的服务次序(对于同一航班的不同航班保障任务,食品车必须优先于摆渡车完成航班保障任务,摆渡车必须优先于客梯车完成航班保障任务)及其充电时间,建立民航电动特种车辆充电调度模型,制定每辆特种车辆的服务开始时间窗,最终完成民航电动特种车辆与等待服务的航班匹配。
1.2 参数描述
M={1,2,…,m}表示电动特种车辆种类集合;
Ni表示第i 种电动特种车辆的数量;
Cij表示第i 种电动特种车辆第j 辆车;
F={1,2,…,f}表示需进行航班地面保障服务的航班集合;
P={1,2,…,p}表示可供电动特种车辆进行电量补给的充电桩集合;pij表示第i 种电动特种车辆第j辆车在p 充电桩进行充电;
Tijb和Tije分别表示第i 种电动特种车辆第j 辆车开始充电的时间和完成充电的时间;
Tijf和Tij(f+1)分别表示第i 种电动特种车辆第j 辆车服务航班f 的结束时间和服务航班f+1 的开始时间;
Sc表示电动特种车辆充电速率;
Eij和Eijsoc分别表示第i 种电动特种车辆第j 辆车在充电期间增加的电量和剩余的电量;
Qif表示航班f 的第i 种电动特种车辆服务所需电量(无负载运行电量和航班保障服务电量);

αif和βif分别表示航班f 接受第i 种电动特种车辆的航班保障服务的最早开始时间和最晚开始时间;
xijf表示第i 种电动特种车辆第j 辆车是否正在进行航班f 保障服务任务,即

yijf表示完成航班f 保障任务的第i 种电动特种车辆第j 辆车是否继续进行下一航班保障任务,即

1.3 模型规则制定
针对民航电动特种车辆进行充电调度管理研究,并制定如下规则:①每种电动特种车辆数量给定并不再改变;②每种电动特种车辆服务时间给定并不再改变;③任一特种车辆的航班保障服务开始后,完成之前不会中断;④任一架航班的每种服务一次只需要一辆特种车辆完成;⑤每个充电桩可同时为两个电动特种车辆进行充电;⑥同一车辆完成的相邻两个航班保障任务之间需预留5 min 空余时间。
1.4 电动特种车辆充电调度模型构建
1)目标函数
最小化电动特种车辆总数量,即

最小化电动特种车辆充电时间,即

2)约束条件

式(3)表示每架航班只能由一种类型车辆中的一辆特种车辆进行服务;式(4)表示同一辆电动特种车辆同一时间仅可进行一个航班的保障服务任务或无航班保障服务任务;式(5)表示第i 种电动特种车辆第j 辆车完成充电后5 min 内要开始航班f 的航班保障任务;式(6)表示当yijf=1,则可以进行下一航班保障任务,当yijf=0,则选择充电桩进行充电;式(7)表示航班f + 1 任务开始时间应在航班f 任务完成之后5 min;式(8)表示充电桩p 最多可为2 辆电动特种车辆同时进行充电;式(9)表示充电期间第i 种电动特种车辆第j 辆车补充的电量。
2 电动特种车辆调度模型求解
上述所提的民航电动特种车辆充电调度管理问题是一个组合优化问题。对于这类优化问题,通常很难通过数学方法得到一个最精确的解,由于问题规模增大,所以通常只能得到问题的多个可行解,即“非劣解”,称其为Pareto 最优解,且多目标组合优化问题一般会得到多个Pareto 最优解。
目前,大规模的组合优化问题常用群智能算法来解决,常用的群智能算法有粒子群优化、蚁群优化、鱼群算法等。而粒子群优化算法更适合本研究的特性。因此,在解决民航电动特种车辆充电调度管理问题时,采用多目标粒子群优化算法进行求解。
2.1 多目标粒子群优化算法
标准的粒子群优化算法的流程如图1 所示。

图1 粒子群优化算法流程图Fig.1 Flow chart of particle swarm optimization algorithm
(1)设置种群参数、变量范围等相关参数,并随机将一群含有位置和速度信息的粒子均匀分布在给定的寻优空间中并进行初始化。
(2)计算群体中每个粒子的适应度值。
(3)对每个粒子的适应度值都要与之前找到的最优适应度值进行比较,如果当前位置较好,则将个体最优位置设置为这个粒子的位置,然后更新种群最优位置。
(4)根据粒子速度和位置更新公式更新粒子的速度和位置如下

式中:i 表示粒子序号;k 表示迭代次数;d 表示D 维空间中坐标序号;c1和c2是取值范围为1~2 的常数,用于表示个体和种群历史信息对粒子运动行为的影响;rand 是0~1 的随机数表示个体最优位置表示种群最优位置;xk表示粒子当前的位置。式(10)包括3 个组成部分:第1 部分表示粒子当前速度,为下一代粒子提供飞行指示;第2 部分表示粒子认知,避免落入局部最优求解的情况出现;第3 部分表示粒子受群体信息影响进行交互式学习。
(5)判断给定的终止条件是否满足。若满足,则停止,并输出最终得到的结果;否则回到步骤(2)继续检索。
2.2 模型求解
考虑航班保障任务所需电量的民航电动特种车辆充电调度的具体求解步骤如下。
(1)航班时刻表统计。对某机场当日航班离港时刻进行记录。
(2)航班保障任务车辆次序规定。根据相关规定对不同类型航班保障任务车辆的次序进行规定。
(3)机场内信息系统数据输入。机场内信息系统数据包括电动特种车辆数量、电池容量、起始剩余电量信息和充电桩数量及其充电功率大小等。
(4)参数设置。设置多目标粒子群优化算法参数,其中种群规模设置为100,最大迭代次数设置为50。
(5)种群编码与初始化。种群采用整数编码,种群维度为航班数量×所需车辆种类数目,每个个体元素表示该航班分配的各类车辆的编号。初始种群在车辆编号范围内随机生成,计算初始适应度,每个个体的适应度值有两个,即电动特种车辆种类数量和电动特种车辆充电时间,同时个体需满足约束条件。
(6)确定是否已经达到最大循环迭代次数,如果未达到迭代次数,则将迭代次数增加1,然后转到步骤(5)以更新调度策略。
(7)计算完成,输出最终达到满足条件的结果。
3 实验数据
针对上述民航电动特种车辆充电调度管理这一课题的研究,利用多目标粒子群优化算法,并通过Matlab2018b 软件进行仿真。以国内某机场一天中7:45—22:40 内的航班离港时刻数据为例,实现该机场民航电动特种车辆的调度管理,并验证民航电动特种车辆充电调度模型和多目标粒子群优化算法的可行性。
3.1 民航电动特种车辆数据
该机场此时间段内有摆渡车10 辆、行李传送带车25 辆、客梯车15 辆、清水车15 辆、污水车15 辆、食品车10 辆,总计90 辆民航电动特种车辆可为离港航班的地面保障服务使用。车辆行驶速度为20 km/h[15]。所有车辆电量剩余初始值在35%~65%内随机分布。上述车辆从20%(欠电状态)到100%(满电状态)的充电时间为3.5 h。车辆进行一次航班保障服务任务所需电量为:摆渡车3%;行李传送带车4%;客梯车4%;清水车2%;污水车2%;食品车3%。该时间内有10 个充电桩(20 个充电枪)可为上述车辆进行充电。车辆在电量≤20%时前往充电桩充电,电量为20%~60%之间的车辆可在空闲时间超过30 min 时进行充电,其中电量最低的优先充电。
3.2 航班保障服务数据
经过对国内某机场调研,该机场在当日7:45—22:40 之间的航班离港时间如表1 所示。表2 分别为摆渡车、行李传送带车、客梯车、清水车、污水车、食品车对各离港航班进行地面保障服务开始时间窗,每辆车须在时间窗内开始对航班进行服务。

表1 部分航班离港时刻表Tab.1 Departure schedule of some flights

表2 航班保障服务开始时间窗Tab.2 Time window for the start of the flight support service
不同类型航班地面保障车辆所需的平均服务时间均有所不同,根据具体的机场调研得到摆渡车、行李传送带车、客梯车、清水车、污水车及食品车单次进线航班保障服务任务的平均时间分别为:15、15、15、5、5、10 min。
6 种类型特种车辆的调度分别属于客舱服务和货舱服务,由于在服务期间服务对象相同的需要遵守一定的次序关系,各类型航班保障车辆之间的次序关系如图2 所示,其中,清水车须在污水车服务结束之后进行,食品车完成服务之后,摆渡车与客梯车开始进行工作,行李传送带车单独服务于货仓,无需考虑其次序关系。
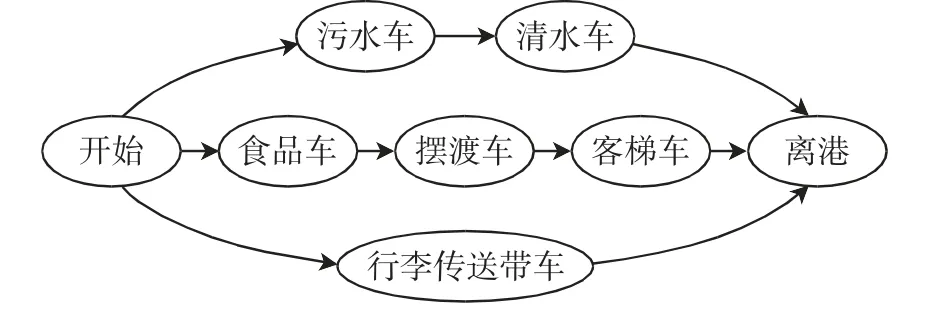
图2 各类型航班保障服务车辆次序关系Fig.2 Sequence relationship of vehicles for various types of flight support services
4 实验结果分析
采用MOPSO 算法对所述民航电动特种车辆充电调度模型进行求解,在最终得到的车辆总数量及充电时间的Pareto 解中选取3 组解,如表3 所示。

表3 车辆总数量及充电时间的Pareto 解Tab.3 Pareto solution of total number of vehicles and charging time
针对所得的Pareto 解,对最终方案选取的原则为:首先要满足在航班离港时间之前,各类型车辆尽可能地在服务时间窗内完成航班保障任务,同时尽可能减少特种车辆的数量及特种车辆的充电时长。经过比较,最终选取车辆总数量为85 辆,充电时间为5 230 min这组解。
在该组解中:所有民航电动特种车辆的初始电量在35%~65%之间随机分布如表4 所示;各类型民航电动特种车辆每辆车对应的服务航班编号如图3 所示;各类型车辆每辆车的充电时间如图4 所示。
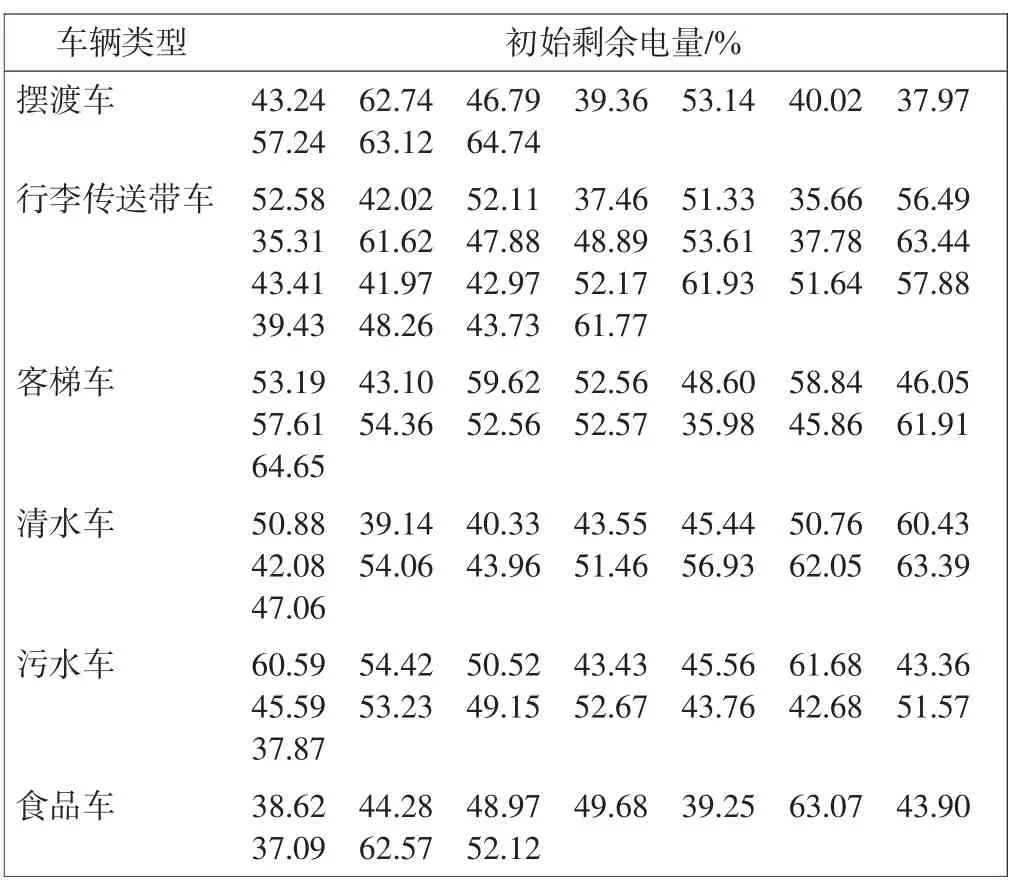
表4 电动特种车辆初始剩余电量Tab.4 Initial residual power of electric special vehicles
以图3(a)及图4(a)中4 号摆渡车为例,在这一时间段的航班保障任务开始之前,4 号摆渡车所剩电量为39.36%,在其完成7 号航班的乘客输送任务之后,该辆摆渡车选择在7:05—9:33 之间的时间段内进行148 min 的充电,这段时间所补给的电量足够4号摆渡车完成其在当日9:33—22:40 时间段内剩余的航班保障服务任务。
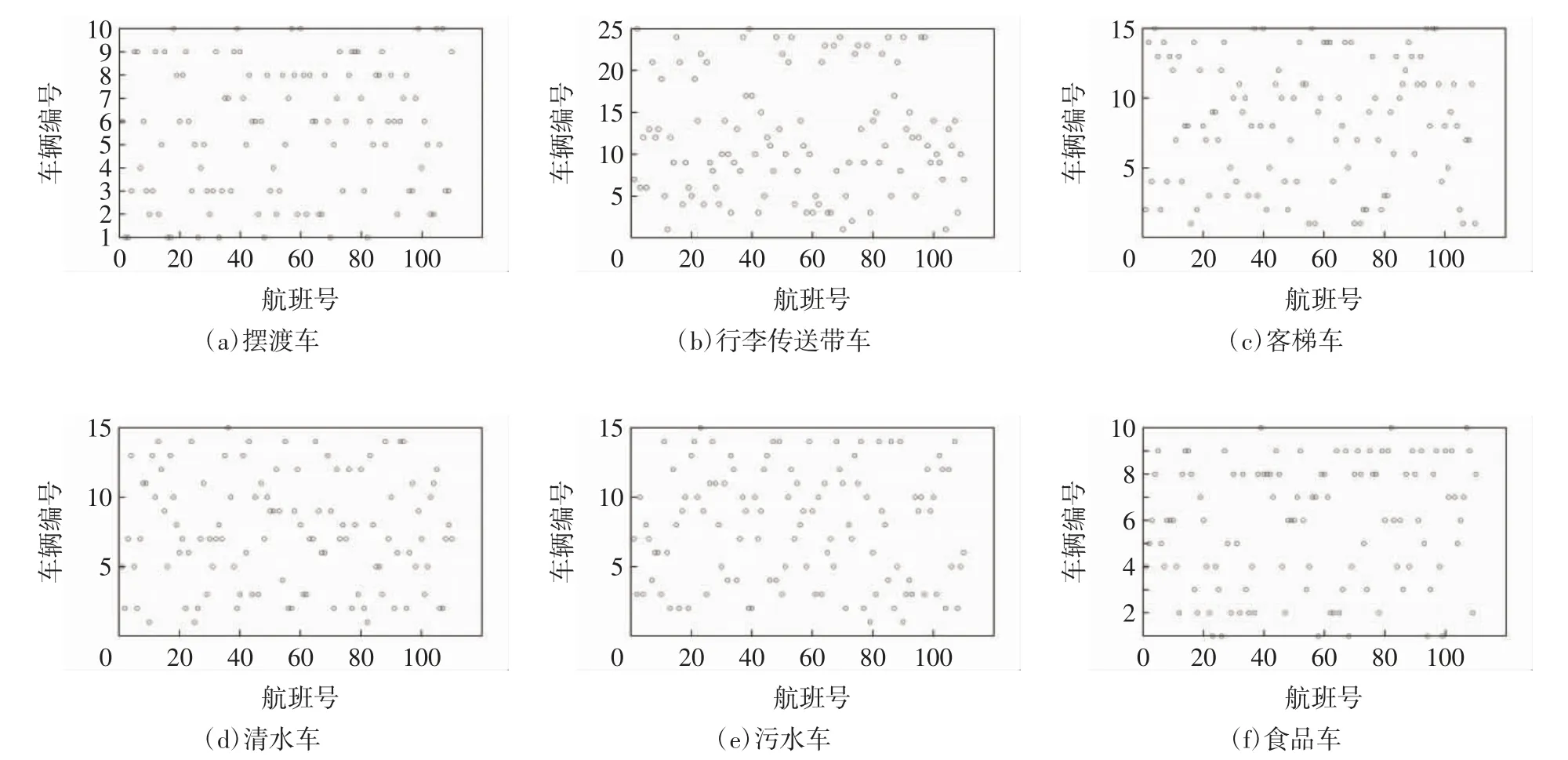
图3 电动特种车辆服务对应航班号Fig.3 The flight number corresponding to the electric special vehicle service

图4 电动特种车辆充电时间Fig.4 Charging time of electric special vehicles
根据整体航班保障服务任务所需电量的计算与统计,使得每辆民航电动特种车辆的服务任务及充电时长有了更明确规定。其中在当日的航班保障服务期间共有52 辆电动特种车辆在此时间段内需要补充电量,若不对充电时长进行规定,车辆每次充电都达到满电状态才停止充电,则所需总充电时长为6 124 min;而当电动特种车辆根据后续航班保障任务所需消耗的电量进行对应的电量补给,则总体充电时长缩短至需5 230 min,相比较节省了14.60%的充电时长,为112个航班提供服务时,减少了5 辆电动特种车辆。
5 结语
为了适应当前机场特种车辆从燃油车辆转电动车辆的趋势,通过分析航班地面保障任务的业务流程,对不同类型民航电动特种车辆进行次序约束,结合航班离港时间及充电桩的使用,以减少机场民航电动特种车辆的数量和充电时长为目的,采用MOPSO 算法,利用Matlab 仿真验证所述的民航电动特种车辆充电调度模型,实验证明,所提调度策略不仅减少了民航特种车辆数量还可以明显缩短车辆的充电时长,较好地解决了民航电动特种车辆充电调度问题。
在实际工作中可能还会有天气环境等因素影响机场车辆调度,下一步将对此进行深入研究。

