基于改进Voronoi图的终端扇区动态规划研究

郭宇帅

（民航局空管局运行管理中心，北京 100022）

随着国内航班量的不断增长，最初的终端区规划已不能适应当前民航业发展需求。空域规划不合理会增大管制员在某个扇区内的工作负荷，从而导致扇区间的管制复杂程度出现不均衡状态，会进一步降低航班正常率，影响旅客的出行质量。

终端区空域规划是空中交通管理的重要组成部分。国外对终端区空域规划研究开展较早，Trandac 等[1]针对动态空域划分问题，提出一种基于克尼丁算法增益概念的图划分启发式方法，可在短时间内为大规模实例寻找合理且良好的初始解，但并未从节点中确定扇区的确切边界。Yousefi[2]将美国国家空域分解为3层，然后将空域划分为航路交通管制中心（ARTCC，Air Route Traffic Control Center），并在每个ARTCC 中继续进行分区，以构建最佳扇区边界。Sabhnani 等[3]提出一种利用高度进行三维扇区划分的方法，并提出一种符合交通流切割的方法。Gerdes 等[4]提出一种处理非凸空域边界的划分方法，并实现了动态扇区划分。国内对终端区空域规划研究开展相对较晚。张慧[5]引入飞行航段理论，通过Voronoi 图对空域进行有限元切割，并对上海终端区进行了优化。贾铧霏[6]提出一种基于均衡静态复杂度的空域划分方法，并基于西安05 号扇区进行验算。宁亚美[7]将扇区划分方法总结为Voronoi图剖分方法和航段划分方法，并利用太原终端区对两种方法进行了算例验证。高伟等[8]通过谱聚类对太原空域关键点进行聚类，并建立了扇区划分模型，解决了管制扇区划设时协调负荷过大的问题。

综上，通过对国内外研究发现，终端区扇区动态规划存在未结合实际交通流进离场特性和剖分扇区未考虑航路点权重等问题。基于以上问题，本研究提出基于改进Voronoi 图的终端扇区动态规划研究方法，从结合实际交通流进离场特性与引入关键点权重方面入手，通过改进Voronoi 图水平划分，运用改进蚁群算法将终端区管制工作状态按时间段分为3 种交通流情况，并对每种交通流情况建立模型，最终建立扇区动态规划模型，使终端区扇区动态规划更符合实际运行情况，可为提升管制工作效率提供借鉴。

1 基于权重的Voronoi 图

根据文献[6]不难发现，终端区空域规划一般采用Voronoi 图进行划分，但Voronoi 图的原理是将各节点视为具有相同权重的节点，即各航路点被视为同等重要，但这种规划方式非常不符合实际情况。在空域规划中，有的航路点联接多条航路，其复杂程度必然高于联接航路较少的航路点。因此，将航路点设置为不同权重符合空域规划的实际情况，因此，本研究采用基于权重的Voronoi 图对终端区进行空域规划。

1.1 Voronoi 图构成

根据文献[4]，Voronoi 图可将二维平面分割为若干个凸多边形，其基本原理是画出每相邻两个点的垂直平分线，由这些垂直平分线将二维平面分割成为不同的凸多边形，二维平面上每个点都与其最近的关键点有关系。也就是说，该凸多边形内的点到该凸多边形上关键点的欧式距离最近。

一般常用的Voronoi 图构造方法为对偶生成法，其构造过程为：先找出不共线的相邻3 点，形成三角剖分；然后基于欧氏距离，对每个三角形上的3 条边作出其垂直平分线，这3 条垂直平分线便构成了正交中心，这些正交中心便是Voronoi 图的边界交点，分割的边界则为这些垂直平分线，Voronoi 图结构如图1 所示。

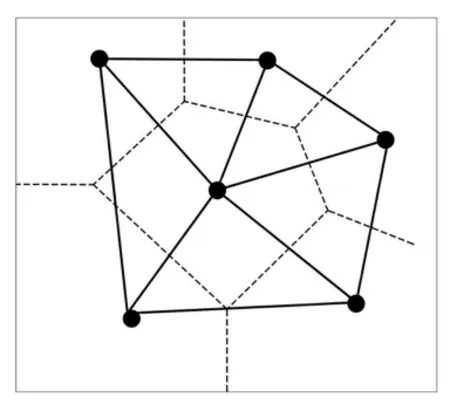
图1 Voronoi 图结构Fig.1 Structure of Voronoi diagram

1.2 关键点权重设置

将终端管制区看作平面，终端区内的航路点看作关键点，但每个航路点所联接的航路数量是不相同的，所以每个航路点的重要程度也各不相同。因此，管制员在对航空器进行航空管制时，每个航路点的管制复杂程度也会不同。

故本研究引入权重概念，设平面内关键点的集合d={p1，p2，…，ph}，其中pk（k = 1，2，…，h）为第k 个区域块的关键点，pik为Voronoi 划分区域第k 个区域块内的一点，根据Voronoi 图的分割性质，可以得出该点距离关键点pk小于到其他关键点pj，即

D（pik，pk）≤D（pik，pj） j≠k j≠i j=1，2，…，Z

式中：D 表示欧式距离；pj表示pk以外的关键点。

设每个关键点的复杂程度为qk，k=1，2，…，h，则关键点的权重Qk可表示为

根据式（1）得到关键点的权重，则可将相邻关键点的距离由欧氏距离改为权重距离，则权重距离可表示为

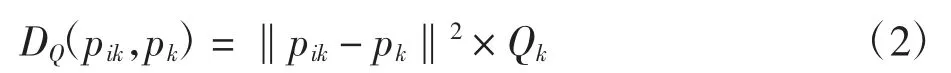
本研究将权重引入，将普通Voronoi 图中的欧氏距离相等改为权重距离相等，设原始三角剖分的边为e，运用权重距离得到两相邻关键点的垂直平分线e′，则该垂直平分线e′就是三角剖分的对偶边，将所有的对偶边依次相连，从而得到新的凸多边形。

2 终端扇区动态规划模型

2.1 目标函数

从几何角度出发，终端区空域都可以视作不规则的多边形，经过引入权重的Voronoi 图处理，可以得到m 个区域块。假设规划n 个扇区，那么便可转化为数学问题，即如何将m 个区域块合理地划入n 个扇区集合中。在确定扇区个数后，从实际工作出发，为最大限度均衡各扇区的管制复杂程度，以各扇区间管制复杂程度的标准差，建立目标函数，标准差越小，则各扇区间复杂程度越均衡，即

式中

式中：Fj表示第j 个扇区的复杂程度表示n 个扇区的平均复杂程度；fi表示第j 个扇区内第i 个区域块的复杂程度。

在实际工作中，终端区的进场架次不可能总是与离场架次大致相同，其具体分成3 种情况：离场架次明显多于进场架次（FD＞FA）、进离场架次数量基本一致（FA≈FD）、进场架次明显多于离场架次（FA＞FD）。

为实现各扇区管制复杂程度相对均衡的目标，当FD＞FA时，应着重考虑离场航线的扇区划分；当FD≈FA时，应平衡考虑进场、离场航线的扇区划分；当FD＜FA时，应着重考虑进场航线的扇区划分。

2.2 约束条件

在实际工作中，设定定量约束条件如下。

1）几何连通性约束

管制工作扇区应为一个完整连续的单元主体，即不能出现中间为2 号扇区，左右两侧为1 号扇区的情况，即

式中：ξij为整数约束，即第j 个扇区是否包含第i 个区域块，若包含则为1，若未被包含则为0；hi为第i 个区域块所邻接的区域块集合。

2）几何唯一性约束

每一区域块只能被包含在唯一扇区内，即该区域块不能同时被包含于1 号与2 号扇区内，即

3）几何完整性约束

所有的区域块都应被包含在划设的扇区内，即区域块不能未被包含，即

除此之外，扇区规划还应满足航空器进入扇区不小于最低飞行时间和避免航空器多次转换无线电频率进入不同扇区，这些约束将作为手动修正的依据。

3 改进蚁群算法

根据文献[9]，蚁群算法具有正反馈性、强鲁棒性的优点，但该算法收敛速度较慢，不易得出全局最优解，为了解决上述缺点，设置动态信息挥发参数。

蚁群算法有以下参数：信息素参数α，信息素挥发参数ρ，信息素强度Q，启发式函数参数β 等。

针对于本目标函数，面向扇区动态规划的蚁群算法具体步骤如下。

（1）根据终端区实际管制工作特点，假设有x 只蚂蚁，需要放在x 个离散点上，为实现基于进离港流量分布的终端扇区动态规划，将分为以下3 种情况确定蚂蚁爬行起点：①针对离场架次明显多于进场架次的情况，蚂蚁爬行起点应设置在离场关键点上；②针对进离场架次数量基本一致的情况，蚂蚁爬行起点应均匀设置在进离场关键点上；③针对进场架次明显多于离场架次的情况，蚂蚁爬行起点应设置在进场关键点上。

（2）确定第i 个关键点和与之相邻联接的关键点Ei，生成邻接矩阵，1 表示两点相连，0 表示两点不相连。

（3）根据两点的连通情况得到蚁群禁忌表utab，将该表设为s。

（4）根据设定，蚁群只会选择相连的点作为即将前往的下一点，则第x 只蚂蚁选择下一点的概率为

式中：Ax表示第x 只蚂蚁选择下一点的可行集合；τiu（t）表示在第t 次迭代中由点i 到点u 信息素的大小；κiu（t）表示在第t 次迭代中由点i 到点u 蚂蚁的启发性因素；fu为该关键点所在区域块的管制复杂程度。

当每完成一次爬行，其信息素更新为

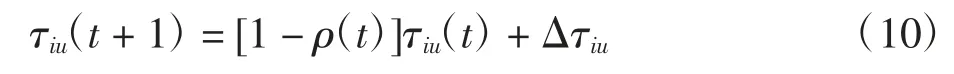
式中

式中：M 表示当前完成的迭代次数；Tx表示第x 只蚂蚁走的下一个关键点；E（i，u）为该蚂蚁从点i 到点u所经过的路线。

传统蚁群算法中信息素挥发参数为固定数值，这易陷入局部最优解，为加快寻找全局最优解，故设置ρ值为自适应函数，即

式中0.3≤ρ≤0.6。

（5）当所有航路点均被x 只蚂蚁爬行完成，输出本轮解。

（6）如果经过判断未达到最初设置的迭代次数，则次数加1，转回步骤（1）继续输出。

（7）根据不同时间段的动态进离场分布情况，得到扇区最优动态规划方案。

4 算例分析

4.1 参数设置

基于2020年8月昆明终端区管制数据，所有数据均来自管制自动化系统雷达数据。将终端区内航路点看作划分扇区的关键点，将各点的经纬度转为二维直角坐标系下的点，且坐标系内的原点（0，0）为跑道基准点。

基于昆明终端区历史航班架次统计数据，昆明终端区2020年8月平均每小时的进离港架次分布，如图2所示。

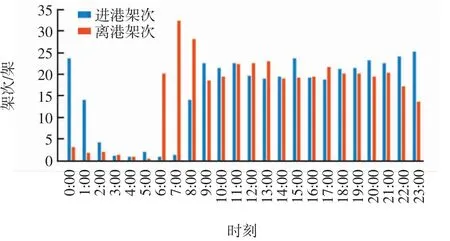
图2 昆明机场平均小时进离港架次分布Fig.2 Distribution of average hourly arrivals and departures at Kunming airport

通过对图2 分析可发现：2:00—5:00 时段中，进离场架次明显偏少，故不予考虑；6:00—8:00 时段属于离场架次明显多于进场架次的时段；9:00—21:00 的时段中，进离场架次数量基本一致，因此将该时段看作进离场均衡的时段；在22:00—次日1:00 时段中进场架次明显居多。

蚁群算法的参数设定为：信息素参数α=1，信息素初始挥发参数ρ=0.6，信息素强度Q=20，启发式函数参数β=1，迭代次数为100 次，划设扇区数量为5。

如果航路关键点所联接的航路越多，则该点的管制复杂程度越高，故将各个关键点的管制复杂程度数值设置为其联接的航路个数，如表1 所示。

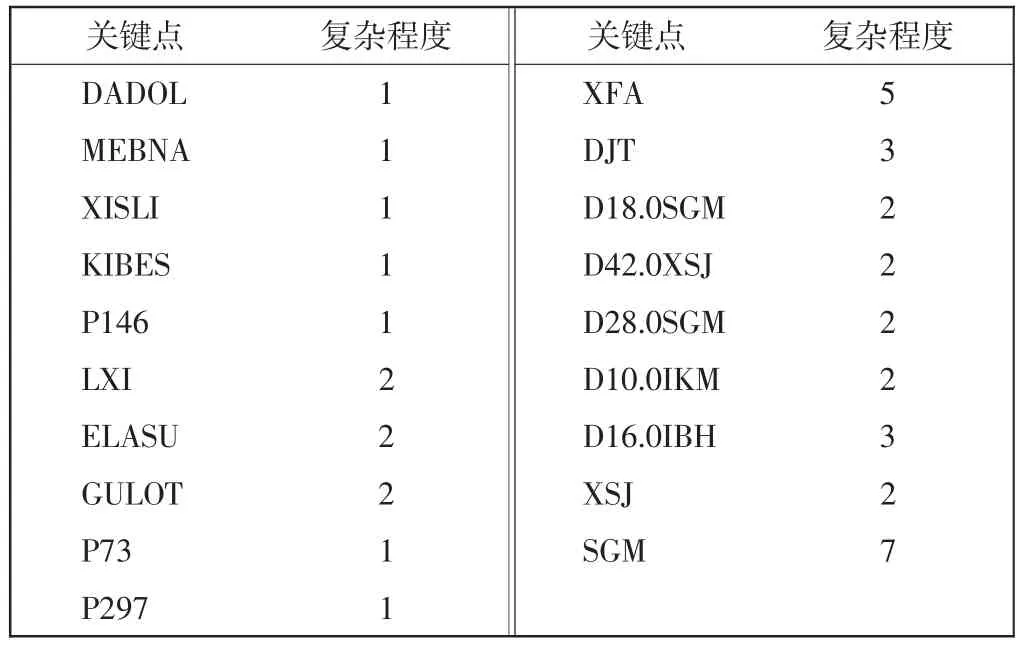
表1 区域块关键点复杂程度Tab.1 Complexity of area block key point

4.2 仿真结果

将昆明终端区的关键点坐标数据导入Matlab 中，通过基于权重的Voronoi 图剖分，并把各关键点所划分的区域块用序号进行标记，该空域共有19 个关键点，故每个区域块用序号1～19 表示。各区域块的红点表示关键点的所在位置，结果如图3 所示。

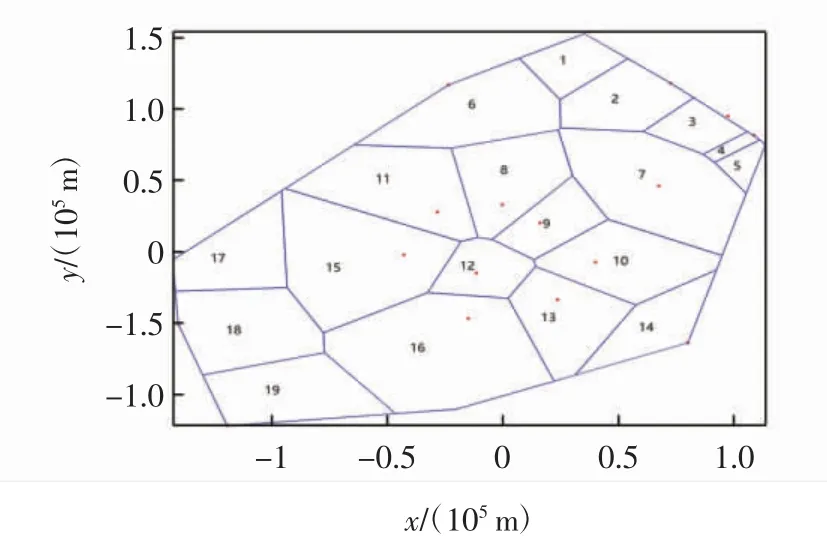
图3 昆明终端空域剖分结果Fig.3 Dissection result of Kunming terminal airspace

（1）在6:00—到8:00 时段内，由于离场架次明显居多，为了尽可能减少离场航路出现在同一个扇区内，爬行起点选为离场航路关键点，该时段扇区规划结果如表2 所示。经计算，该时段最优划分结果的均衡程度为1.469 7。

表2 6:00—8:00 时段扇区划分输出结果Tab.2 Sector division output results at time 6:00-8:00

（2）在9:00—21:00 的时段内，由于离场架次大致等于进场架次，爬行起点选为昆明终端区所有关键点，该时段扇区规划结果如表3 所示。经计算，该时段最优划分结果的均衡程度为0.748 3。

表3 9:00—21:00 时段扇区划分输出结果Tab.3 Sector division output results at time 9:00-21:00

（3）在22:00—次日1:00 时段内，进场架次明显居多，为尽可能减少进场航路出现在同一个扇区，爬行起点选为进场航路关键点，该时段扇区规划结果如表4 所示。经计算，该时段最优划分结果的均衡程度为1.326 6。

表4 22:00—次日1:00 时段扇区划分输出结果Tab.4 Sector division output results at time 22:00-next day 1:00

优化前后各时段内扇区动态规划得出的复杂程度[9]对比如图4 所示。

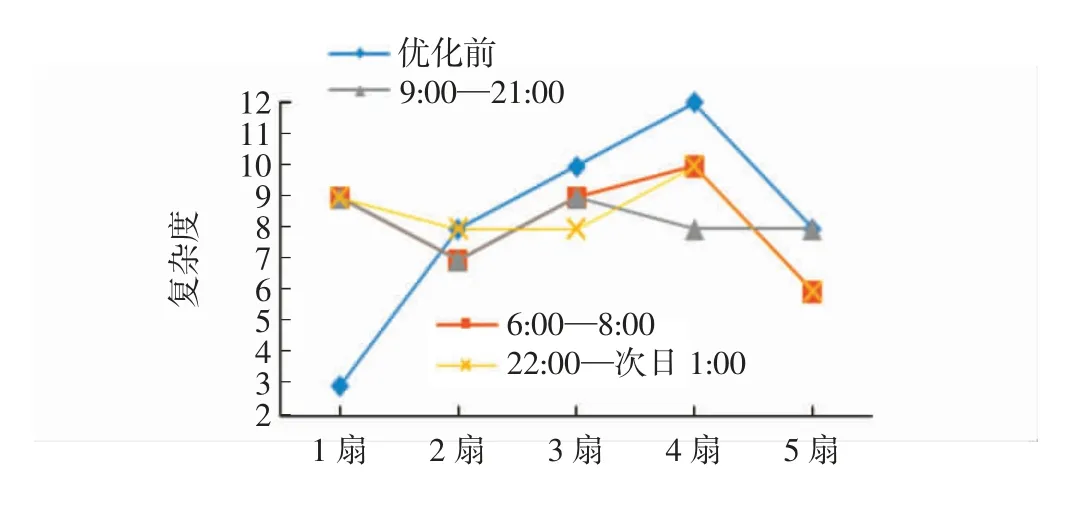
图4 优化前后复杂程度对比Fig.4 Comparison of complexity before and after optimization

从图4 可看出：优化前，1 扇复杂程度最低，4 扇复杂程度最高，分配极不平均；经过扇区动态规划后，5 个扇区的复杂均衡程度有了极大提高，验证了模型的有效性。

5 结语

本研究提出一种基于改进Voronoi 图的终端扇区动态规划方法。首先，通过引入权重概念，用改进后的Voronoi 图对终端区进行剖分，形成了初步的分割模块；其次，根据终端区流量特点，考虑进离流量分布不均的时隙特点，从实际工作出发构建了扇区动态规划模型；最后，基于改进的蚁群算法，根据进离场流量变化情况分别划分扇区，通过不同的区域块组合方式，达到动态规划扇区的效果，同时基于昆明终端区数据，验证了该动态规划模型的可行性与有效性。