基于DEA模型的空中立交桥效益分析评价

王莉莉，胡启伟

（中国民航大学空中交通管理学院，天津 300300）

近年来，随着航空运输业的快速发展，航路交叉点日益增多，中国提出了空中立交桥的概念并进行实施。空中立交桥的发展对于未来空域规划具有重要意义，为了衡量搭建空中立交桥的合理性及其运行参数是否被充分利用，需要对其搭建效益进行评价。因此，将各运行参数加入效益评价分析模型，测算各地区的评价结果，为未来空中立交桥的合理规划提供参考。

国外并没有空中立交桥的概念，但国外的相关研究主要有：Hering[1]在对欧洲空中交通流分布情况分析的基础上，总结了欧洲已有的3 种空域结构设计理念，初步探讨了欧洲空中高速路的设置方法，其中提到的高速路交叉点采用不同高度分离开的观点；Hoffman等[2]总结了各类航路的设计概念，将管道理论拓展，定性地总结出了空中高速路设计上需要解决的位置、运行、激活、匝口管理等问题，初步分析了可增加的容量；Chen 等[3]研究了管道航路的激活问题，提出只有交通流量超出容量足够大时，才适合于激活管道航路；Xue[4]在空中走廊的设计分析中综合多方面因素，提出了空中走廊运行模型，还分析了其对非走廊交通的影响。国内相关研究包括：杨超[5]阐述了单向循环航路改造对空中立交桥的影响，并分析了空中立交桥的成因、利弊，以及影响空中立交桥搭建的因素；位放[6]研究了空中航路交叉点的定量分级方法，给出了分级为枢纽、繁忙的航路交叉点应建立空中立交桥的建议；戴福青等[7]通过建立新型空中立交桥对航路交叉点进行优化，解决交叉点对航路容量的限制问题，达到航路扩容的目的。但国内对于空中立交桥运行效益的评估研究较少。数据包络分析（DEA，data envelopment analysis）法是效益评价的一种手段。李美娟等[8]叙述了DEA 的思想、模型和应用步骤，总结了近20 多年DEA的发展和主要应用领域。黄彩德[9]研究分析了铁路安全投入与效益之间的关系。综上分析，也可将DEA 模型与空中立交桥运行参数建立联系。

本研究主要针对空中立交桥的搭建点进行了分析，在采集到的数据中进行输入指标和输出指标的选取，并通过DEA 模型进行效益评价。最终的计算结果可作为该处搭建空中立交桥是否合理的参考标准之一，为空中立交桥的搭建提供理论支持。

1 数据包络分析法简介

1978年Charnes 等[10]提出了一个数学结构和一个线性规划模型，这个模型被称为“数据包络分析法”。DEA 是一个强大的优化工具，用于衡量任何单位或部门在技术和规模方面的效率，其将决策单元与前沿边界上的目标进行比较。前沿是指基于当前数据集的最佳实践前沿，而有效前沿线（也称有效边界）是指连接最有效点的线。有效前沿线包围其他数据点，这就是为什么该方法被称为“数据包络分析法”。DEA 是一个多标准决策工具，在应用DEA 模型之前，需要选择一组决策单元（DMU，decision making units），DMU 在DEA模型中指定被评估或基准测试的单位，这些单位可以是农场、公司、医院、银行、大学、产品、城市、政府、航空公司等。最终，DEA 被用作绩效评估和参照为最佳做法而制定的基准方法。DEA 是一种具有相对有效性的综合评价方法，在对评价对象做出评价时，与选取的投入（输入）指标和产出（输出）指标的量纲无关，因此使用DEA 建立模型之前并不需要对原始数据进行量纲化处理[9]。适用于多投入、多产出问题的DEA 模型即使不确定输入和输出之间的线性或非线性关系也可以得到最终的结果。

在对空中立交桥的运行参数进行分析的过程中，将运行参数分为输入指标和输出指标，然后通过DEA进行评价分析研究。

2 DEA 的应用步骤

为了比较各个地区空中立交桥的效益，使用DEA模型进行评价分析。首先选择决策单元，根据决策单元中采集到的数据进行输入、输出指标体系的建立，选择合适的DEA 模型，然后通过Matlab 程序对已选择的DEA 模型进行计算，最后根据计算结果判断DEA是否有效，若有效，则说明该决策单元达到了效益相对平衡，反之则未达到效益相对平衡，继续确定决策单元进行效益分析。DEA 的具体应用步骤如图1 所示。

图1 DEA 应用步骤Fig.1 Application steps of DEA

3 DEA 基础模型

DEA 作为一个分数规划问题，分数目标函数可以理解为单位虚拟输入的虚拟输出。目标函数的分子是决策单元对所有输出的加权和。多输入多输出方案被扩展到其他决策单元，且虚拟输出和输入之比不得超过1，即用对其最有利的投入和产出权重来评估其绩效的决策单元，限制其自身的绩效比率不超过1。通过Charnes-Cooper 变化，分数规划问题就转化为一个线性规划问题。由线性规划的对偶理论可以得到一个对偶规划，对偶规划的经济含义可以理解为其与生产可能集及有效边界的联系。

有效边界称为“边界线”，边界线显示该单元与其他单元相比的优劣。其他单元的效率是相对于有效边界来衡量的，可通过点与边界线的偏差来衡量，有效前沿作为基准。任何企业或单位的效率都由两部分组成：①技术效率，指企业从给定的一组投入中获得最大产出的能力；②规模效率，指一个企业在给定各自价格的情况下，以最佳比例投入的能力[11]。

C2R 模型是使用最多的允许恒定规模回报的模型。然而，可变规模回报可以建模为向目标函数和单个约束添加常数的C2R 问题。假设有n 个决策单元，每个决策单元都有p 种投入和q 种产出。则第j（j∈1，2，…，n）个决策单元的输入向量和输出向量分别为

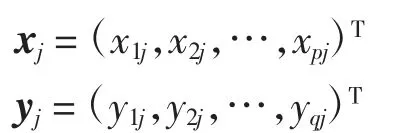
式中：xpj是指第j 个决策单元对其第p 种类型输入值的投入；yqj是指第j 个决策单元对其第q 种类型输出值的产出。设输入和输出权向量分别为

则模型为

式中，j0∈{1，2，…，n}是决策单元集合中某个相对效率值最大的元素。

C2R 模型是把决策单元DMU，j0效率评价系数φj0=看作目标，将所有决策单元的效率评价系数φj0作为约束构造的规划问题，其约束条件为

式（3）是一个分式规划模型，通过Charnes-Cooper 变换，令

则模型转化为

写成向量形式有

上述模型的对偶问题为

式中：n 为决策单元的数量；θ 表示相对效率；λj表示第j 个决策单元的系数；xj表示第j 个决策单元的输入向量；yj表示第j 个决策单元的输出向量。为了便于在经济意义上进行深入研究，要建立对偶模型，设上述问题的最优解为λ*、s*、θ*，其中引进松弛变量s+和s-，将不等式约束条件转化为等式约束

上述问题的最优解λ*、s*、θ*有以下经济学含义：

（1）当θ*= 1，且s+= 0，s-= 0 时，称决策单元是DEA 有效，说明此刻该决策单元最终到达技术有效与规模有效；

（2）当θ*=1，且s+和s-不同时为0 时，称决策单元不是DEA 有效，说明此刻该决策单元最终没有达到同时技术有效和规模有效；

（3）若θ*＜1，称决策单元不是DEA 有效，说明此刻决策单元既不技术有效也不规模有效。

λj值用来评价决策单元在规模方面的收益情况。若存在λj，使得∑λj*=1 成立，则称决策单元的规模收益不变；若∑λj*＜1，则称决策单元规模收益是递增的，相反，规模收益就是递减的。

4 算例分析

4.1 地区空中立交桥介绍

华北地区共搭建了5 架空中立交桥，分别在HUR（怀柔）、VYK（大王庄）、TYN（太原）、ZHO（周口）、WXI（魏县）航路交叉点，这几个航路点流量密集，交叉点的复杂度大。武汉地区空中立交桥是比较典型的空中立交桥，多条航路交叉，物理结构复杂。此外，此处航路网比较复杂，搭建空中立交桥的原则中有1 条为：当航路交叉角度小于30°时，可以看作是一个方向的来流。因此，武汉地区空中立交桥实际上是两架空中立交桥的组合，一个是WHA（天河）交叉点，一个是ZHO（周口）交叉点。其他地区空中立交桥已有航路、航线及高度层信息介绍如下。

DS（叙永）立交桥主要航路、航线：B213、W30、H4、W180、H20、H39。ZHJ（芷江）立交桥东北向航班流可使用高度层：S0890、S1070、S1190、S0810、S0950、S1010、S1130。DYG（张家界）立交桥东向航班流可使用高度层：S0950、S1070、S1190、S1250。ENH（恩施）立交桥东北向航班流可使用高度层：S0810、S0890、S0950、S1010、S1070、S1130。LKO（龙口）立交桥西北向航班流可使用高度层：S0920、S1040。TOL（桐庐）立交桥东南向航班流可使用高度层：S0890、S1010。HO（长武）东北向航班流可使用高度层：S0810、S0950、S1130、S1190。

根据以上地区空中立交桥的信息介绍，选取其中的10 个地区进行效益分析。

4.2 输入和输出指标的选取

首先是对输入和输出指标的选取，将不同地区空中立交桥作为DMU，复杂度表示空中立交桥的复杂程度，决定了投入量的大小，所以作为输入指标。小时风险和全天风险作为输入指标主要是因为空中立交桥的搭建可以减少飞机间的碰撞风险，风险减少可以对投入起到一定的积极作用。而因为空中立交桥的搭建会使小时流量和全天流量产生变化，可以作为一个产出结果，即作为输出指标。指标选取如表1 所示。

表1 输入和输出指标的选取Tab.1 Selection of input and output indicators

要计算一个DMU 的相对效率值并讨论其（弱）有效性，需解1 个线性规划；若要计算所有DMU 的相对效率值，就需要解n 个线性规划，其计算量比较大。所以通过Matlab 程序[12]解决了DEA 模型中大量计算的问题。经过Matlab 程序计算的相对效率值为：E1=0.238 3，E2= 0.333 1，E3= 0.524 1，E4= 0.829 7，E5=0.481 2，E6= 0.981 1，E7= 0.794 9，E8= 1.000 0，E9=0.935 9，E10=1.000 0，如图2 所示。

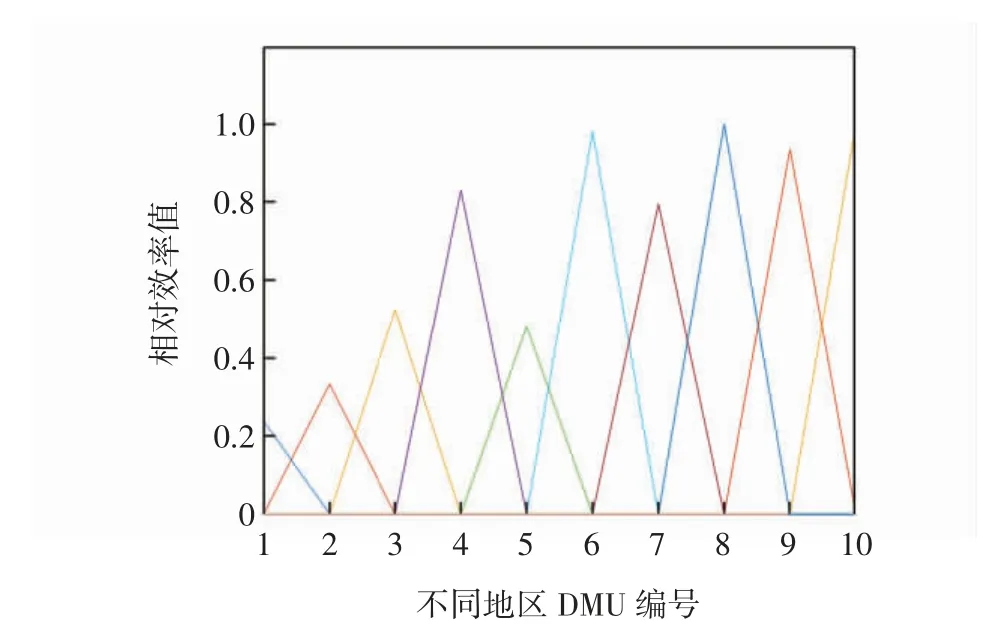
图2 DEA 相对效率值plot 图像Fig.2 Plot of relative efficiency value of DEA model

而在标准的DEA 模型中，有效率的DMU 值均显示为1，无法继续对相同效率值的决策单元进行排序对比，因此提出了超效率评价模型，在超效率DEA 评价中可进一步看出决策单元的有效性排序。通过传统DEA 模型得出两个地区的相对效率值为1，如果要区分相对效率值为1 的地区，就需要超效率DEA 模型来进行计算，同样经过Matlab 程序计算出的结果如图3 所示。

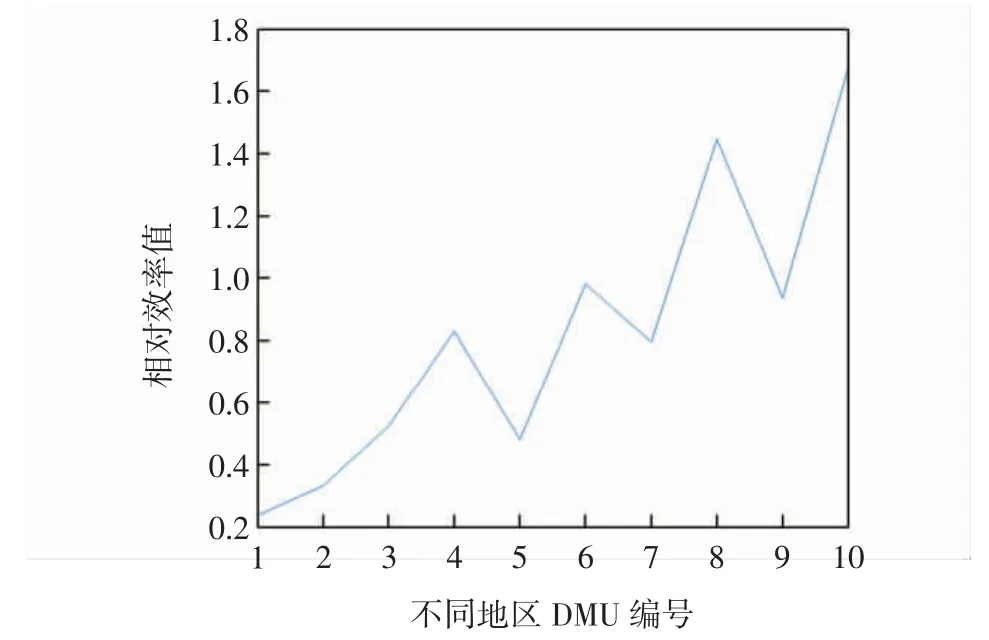
图3 超效率DEA 相对效率值plot 图像Fig.3 Plot of relative efficiency value of super efficiency DEA model

由定义可知，相对效率值达到1，即为弱DEA 有效，因此，DMU8和DMU10至少是弱DEA 有效，DMU1、DMU2、DMU3、DMU4、DMU5、DMU6、DMU7、DMU9是非弱有效的，至于DMU8和DMU10的有效性及其他权向量非有效的原因，这里暂不做分析。所以周口和长武空中立交桥的相对效率值均达到1，即达到了弱DEA 有效，说明这两个地区做到投入和产出的规模相适应，在这两个地方搭建空中立交桥的效益处于最佳状态。通过超效率DEA 模型分析后得出DMU10的效率值又大于DMU8，所以长武的效益又优于周口，所以此方法也可以作为一个效益分析的手段，为搭建空中立交桥提供参考性建议。

5 结语

利用DEA 模型将空中立交桥不同航路点的数据进行分析，通过Matlab 程序进行计算，将不同地区作为DMU，并对DEA 是否有效进行讨论，将结果作为效益评判的标准，即DEA 有效的地区长武和周口是达到效益平衡的，进而通过超效率DEA 模型分析得出长武的效益更优，而非DEA 有效的地区效益平衡方面可能存在不足之处。此方法可为是否搭建空中立交桥提供参考，但对于部分权向量非有效性的原因还有待进一步探讨。