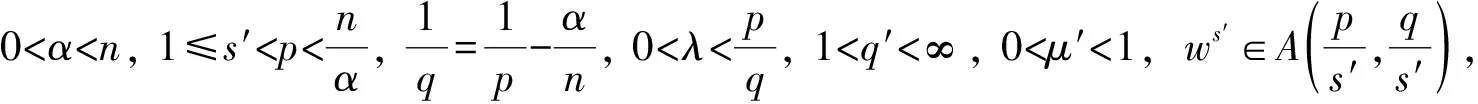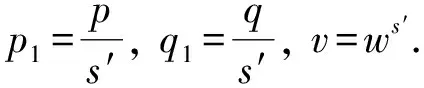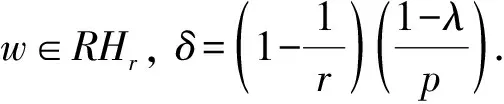混合Morrey空间上Marcinkiewicz积分的加权估计
王 静, 陶双平
(西北师范大学 数学与统计学院, 兰州 730070)
1 引言与预备知识
设Ω在n上零次齐次且满足消失矩条件其中:x′=x/|x|,x≠0;Sn-1为n(n≥2)中的单位球面, dσ(x′)为其上的Lebesgue测度.
固定T>0, 对t∈(0,T), 与时间t相关的Marcinkiewicz积分μΩ定义为
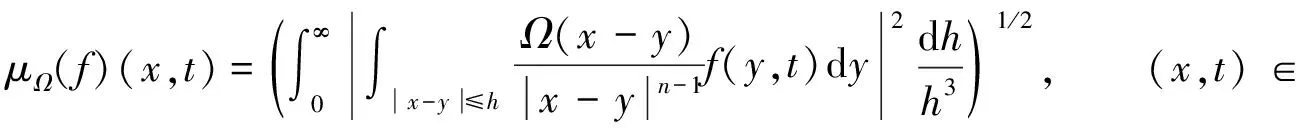
(1)
对于局部可积函数b, Marcinkiewicz积分交换子定义为

(2)
同理, 对t∈(0,T), 0<α (3) 当f(y,t)恒为f(y)时, 上述定义的与时间t相关的Marcinkiewicz积分和Riesz位势即为经典的Marcinkiewicz积分和Riesz位势. 文献[1]得到了经典的Riesz位势在加权Lebesgue空间上的有界性, 进一步的结果可参见文献[2]. 当Ω∈Ls(Sn-1)(s>1),s′ 定义1设T>0, 1 Lq,μ(0,T,Lp,λ(u,v))∶={f(x,t): ‖f‖Lq,μ(0,T,Lp,λ(u,v))<∞}, 其中 这里Bρ(x)={y∈n: |y-x|<ρ}.当u=v时, 简记为Lq,μ(0,T,Lp,λ(u)). 易见, 当权函数u=v=1时, 时空混合范加权Morry空间Lq,μ(0,T,Lp,λ(u,v))即为文献[10]中定义的Lq,μ(0,T,Lp,λ(n)), 且是文献[7]中定义的加权Morry空间Lp,λ(u,v)的一种自然推广. 设1 (4) 则称非负可测函数w∈Ap[2].设1 (5) 设1 (6) 记w∈RHr. 引理2[3]设零阶齐次函数Ω∈Ls(Sn-1)(1 1)s′ 则存在与f无关的常数C>0, 使得对任意的f∈Lp(w), 有‖μΩ(f)‖Lp(w)≤C‖f‖Lp(w). 引理3[4]设零阶齐次函数Ω∈Ls(Sn-1)(1 引理4[13]设w∈Ap且p≥1, 则对任意的球B, 存在一个绝对常数C>0, 使得w(2B)≤Cw(B).一般地, 对任意的λ>1, 有w(λB)≤C·λnpw(B), 其中C与B和λ无关. 引理5[14]设w∈RHr(r>1), 则存在一个常数C>0, 使得对包含球B的任意可测集E, 成立 引理6[15]设b∈BMO(n), 则对任意的1≤p<∞, 有 其中‖b‖*=‖b‖BMO. ‖Iα(f)‖Lq′,μ′(0,T,Lq,λq/p(wq))≤C‖f‖Lq′,μ′(0,T,Lp,λ(wp,wq)). 证明: 设B=B(x0,r)={x∈n: |x-x0| 由引理1和引理4, 可得 下面估计I2(t).由Hölder不等式得 注意到当x∈B,y∈(2B)c时, 有|y-x|~|y-x0|.因此 从而 从而 于是由引理5得 结合I1(t)和I2(t)的估计, 有 对式(7)两边取q′次方, 再在(0,T)∩(t0-ρ,t0+ρ)上积分, 可得 将式(8)两边乘1/ρμ′, 并取上确界, 两边再取1/q′次方, 得 从而 ‖Iα(f)‖Lq′,μ′(0,T,Lq,λq/p(wq))≤C‖f‖Lq′,μ′(0,T,Lp,λ(wp,wq)). 证毕. 定理2设1 证明: 设B=B(x0,r), 类似定理1的证明, 记f=f1+f2, 其中f1=fχ2B.则 由引理2和引理4, 可得 下面估计K2(t).注意到当x∈B,y∈2j+1B(2jB),j≥1时, 2j-1r≤|x-y|<2j+2r成立.因此利用Minkowski不等式和Hölder不等式, 得 再利用球坐标变换, 有 注意到, 如果x∈B,y∈(2B)c, 则|y-x|~|y-x0|.因此可得 从而 由于w∈Ap/s′, 记p1=p/s′, 由Hölder不等式得 因此 于是由引理5可得 结合K1(t)和K2(t)的估计, 有 对式(9)两边取q次方, 再在(0,T)∩(t0-ρ,t0+ρ)上积分, 可得 将式(10)两边乘1/ρμ, 并取上确界, 两边再取1/q次方, 得 ‖μΩ(f)‖Lq,μ(0,T,Lp,λ(w))≤C‖f‖Lq,μ(0,T,Lp,λ(w)). 证毕. 定理3设1 ‖[b,μΩ](f)‖Lq,μ(0,T,Lp,λ(w))≤C‖f‖Lq,μ(0,T,Lp,λ(w)). 证明: 设B=B(x0,r)={x∈n: |x-x0| 由引理3和引理4, 可得 下面估计J2(t).对任意的x∈B, 有 由定理2的证明, 可知 则 因此 由于w∈Ap/s′, 则存在r>1, 使得w∈RHr.因此利用Hölder不等式和引理6, 可得 由式(11)和引理5, 得 下面估计J22. 当x∈B,y∈(2B)c时, 有|y-x|~|y-x0|.由于w∈Ap/s′, 记p1=p/s′, 因此由Hölder不等式和定理2的证明, 可得 于是由引理5有 再由定理2的证明中关于K2(t)的估计, 可知 注意到当b∈BMO(n)时, 有|b2j+1B-bB|≤Cj‖b‖*, 则 因此 结合J1(t)和J2(t)的估计, 得 对式(12)两边乘1/ρμ, 并取上确界, 两边再取1/q次方, 得 ‖[b,μΩ](f)‖Lq,μ(0,T,Lp,λ(w))≤C‖f‖Lq,μ(0,T,Lp,λ(w)). 证毕.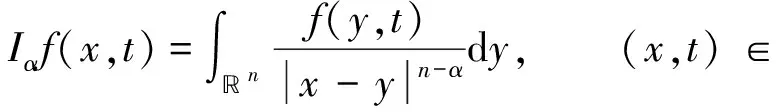
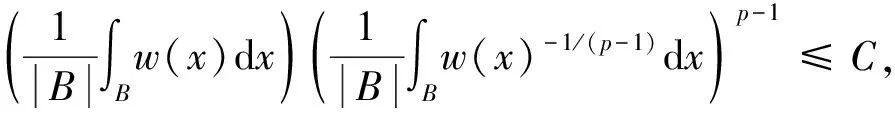




2 主要结果