基于CFD的双向流道泵站压力脉动混沌特性研究

肖忠明，颜红勤，蒋红樱，成 立，刘志泉

（1.丹阳市九曲河枢纽管理处，江苏镇江 212000；2.江苏省水利工程科技咨询股份有限公司，南京 210029；3.扬州大学水利科学与工程学院，江苏扬州 225009）

0 引 言

在我国长江沿岸，为满足灌溉、排涝等要求，建有许多双向流道泵站。该类泵站的特点是流量大、扬程低［1］，同时受长江水位变化影响，易偏离设计工况运行［2，3］。水泵长期偏离设计工况运行，不仅会诱发不良压力脉动［3，4］，导致机组异常振动，而且降低机组运行效率，影响泵站安全稳定性，引发泵站故障［5-7］。

针对轴流泵机组压力脉动特性，国内外许多学者进行了研究［8-12］。王福军、施卫东等［8，9］采用数值模拟的方法研究了轴流泵在不同工况下的压力脉动特性，得出压力脉动幅值在叶轮进、出口随半径增大而增大，导叶中间和出口变化规律则相反，且偏离最优工况越远，脉动的相对振幅越大。张德胜等［10］采用试验的方法研究了轴流泵在不同流量、转速下的压力脉动特性，揭示了轴流泵内部不同位置处压力脉动规律。Al-Obaidi A R［11］研究了轴流泵在不同叶片角度下压力脉动的时域和频域特性，结果表明叶轮叶片角度和非定常流动对压力脉动幅值影响较大。目前对轴流泵压力脉动特性的研究分析方法主要是FFT、小波分析等，此类方法对脉动信号周期性明显的叶轮区域有较好的适用性。但在远离振动源叶轮的区域，如导叶出口、进出水喇叭口、流道等，压力脉动分布规律逐渐变得杂乱无序［13，14］，此类方法适用性较差。混沌理论认为在非线性系统中看似随机不确定性的行为，不是来源于外部环境的随机因素对系统运动的影响，而是系统自发产生的，即具有随机性的运动状态是由确定性方程（内因）直接得到的［15］。许多学者利用混沌理论对泵和水轮机等流体机械进行压力脉动分析和故障预测［16-22］，梁超等［16］对采集的压力脉动信号进行小波包分解，根据混沌特征参数把离心泵汽蚀过程划分为4 个阶段，从不同的角度定量描述动力系统的混沌特性。苏文涛等［17］研究了水轮机在不同空化程度下的压力脉动信号的混沌动力学特征，认为水轮机压力脉动信号中存在混沌吸引子。

以某立式轴流泵站为模型，通过CFD 计算得到设计工况下各监测点的压力脉动时域信号，对其进行相空间重构，利用小数据量法求得最大李雅普诺夫指数，判断其混沌特性，通过求取其分形标度和关联维数，对压力脉动信号的混沌特性进行分析，并对其他两种常用工况进行验证。

1 数值计算模型及计算方法

1.1 计算模型

以某沿江双向流道泵站为计算模型，如图1所示，该泵站设计流量Qopt=20 m3/s，设计扬程H=2.61 m，叶轮直径D=2 550 mm，转速n=150 r/min，叶片数为3片，导叶片数为7片，采用“X”型双层箱涵式进出水流道。

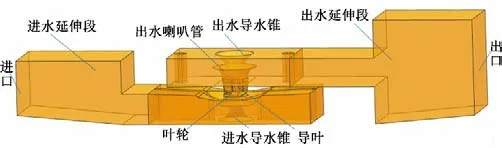
图1 计算模型示意图Fig.1 Diagram of calculation model

1.2 网格划分

对计算模型进行六面体结构化网格划分，对叶轮、导叶及边壁进行加密处理，划分网格数量962.6 万个，整体网格质量控制在0.5以上。叶轮和导叶网格划分示意图如图2所示。

1.3 边界条件设置

CFD 计算采用非定常计算，计算模型进口设为质量流量进口，出口设为自由出流条件；叶轮与导叶、进水流道的交界面采用瞬态动静转子模型。文献［23］的研究结果表明，SSTk-ω模型对流体机械的计算有较好的适用性，因此湍流模型选择SSTk-ω模型，计算收敛精度为10-5。叶轮旋转周期T=0.4 s，取叶轮旋转周期的1/90 为1 个时间步长，即时间步长Δt=3.333 3×10-3s，共计算12个周期。

1.4 测点布置

为监测轴流泵内部压力脉动，在进水喇叭口、叶轮进口、叶轮出口、导叶中部、导叶出口、出水喇叭口截面各布置3个测点，从轮缘至轮毂沿径向分布，共布置18 个测点，测点布置示意图如图2所示。

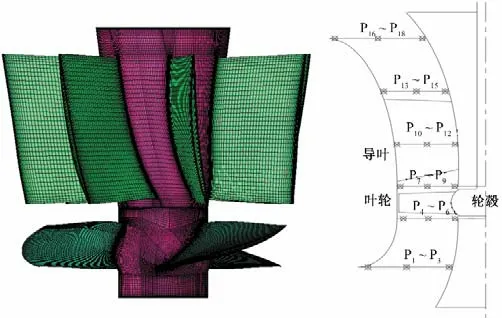
图2 网格划分及测点布置示意图Fig.2 Diagram of grid division and measuring point arrangement

2 外特性验证

在CFX 中对该泵站在0°叶片安放角下的7 个工况进行计算，流 量 分 别 为0.7Qopt、0.8Qopt、0.9Qopt、1.0Qopt、1.1Qopt、1.2Qopt、1.3Qopt，得到其关于流量Q和扬程H、效率η的外特性曲线，并与试验换算得到的原型泵装置性能数据对比，如图3所示。

图3 数模与试验外特性曲线图Fig.3 Curves of numerical simulation and test external characteristics

由图3 可知，数值模拟得到的外特性曲线比试验外特性曲线整体略低，两者变化趋势基本一致。因此，SSTk-ω模型可以较好地预测轴流泵的内部流动，数值模拟计算结果可靠。

3 压力脉动时域信号分析

通过非定常计算得到泵站运行时的压力脉动时域信号，选取径向外缘有代表性的测点P3、P6、P9、P12、P15、P18进行分析，测点的压力脉动时域图如图4 所示，为方便观察，图中均显示后4个周期的时域图。

由图4（a）可知，进水喇叭口处P3点压力脉动波形较乱，无明显的周期性，因为水流从流道进入进水喇叭口时，水流速度、方向改变，使幅值呈现波动变化。由图4（b）、图4（c）可知，叶轮进口P6点周期性规律明显，1 个周期内存在1 个波峰波谷；叶轮出口P9点压力脉动波形复杂，1个周期内有多个波峰波谷，幅值变化较大，此处水流受叶轮和导叶动静干涉作用的影响，流场变化复杂。由图4（d）可知，导叶中部P12点压力脉动变化受叶轮的影响，1 个周期内有3 个波形波谷，与叶片数相对应，幅值发生变化可能与导叶内存在回流等不良流动有关。由图4（e）、图4（f）可知，导叶出口P15点、出水喇叭口P18点距叶轮较远，此处压力脉动规律不明显，但幅值较高，双向出水流道内流态较差，对该处压力脉动的变化产生影响。

图4 测点压力脉动时域图Fig.4 Time-domain diagram of pressure at each measuring point

4 混沌特性分析

4.1 相空间重构

混沌时间序列的判定、分析与预测都是在重构的相空间中进行的，因此相空间重构是混沌特性分析重要的步骤［24］。采用坐标延迟法［24，25］将计算得到的压力脉动时间序列｛x（t）｝，t=1，2，…，N，根据时间延迟τ与嵌入维数m进行相空间重构，得到一组新序列：

式中：t=1，2，…，M；M=N-（m-1）τ。

时间延迟τ采用互信息量法求得，嵌入维数m采用G-P 算法求得，详细计算方法参见文献［24，26，27］。选取有代表性的测点P3，P6，P9，P12，P15，P18点的压力脉动进行相空间重构，得到三维相轨迹图如图5所示。

由图5可知，进水喇叭口P3点相轨迹图无明显规律，从底部至上部呈现扩张规律。根据叶轮进口P6点压力脉动时域图4（b），该点压力脉动周期性最明显，相轨迹图呈收缩状，表现出混沌特性。叶轮出口P9点相轨迹图呈扭转的圆环状，混沌特性明显，对应该点复杂的压力脉动变化。导叶中部P12点相轨迹图呈现螺旋上升的曲线状，该点压力脉动仍具有周期性，但幅值有所变化，使相轨迹图收缩为长条状，序列点自底部至上部离散程度增加。导叶出口P15点、出水喇叭口P18点远离振动源，加之受流道水流变化的影响，压力脉动无周期性，相轨迹图为不规则的长条状。

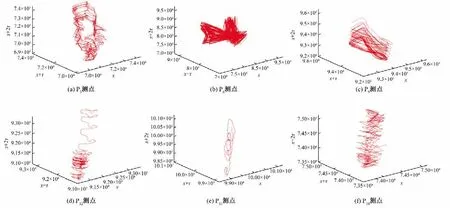
图5 测点压力脉动三维相轨迹图（无量纲）Fig.5 Three-dimensional phase trajectory of pressure pulsation at each measuring point

4.2 最大李雅普诺夫指数分析

李雅普诺夫指数（LE）是混沌的表征量之一，可用李雅普诺夫指数定量分析偏流量工况下的压力脉动信号，判别和验证系统的混沌程度。采用小数据量法［26，27］求解设计流量下的P3、P6、P9、P12、P15、P18号点的最大李雅普诺夫指数。在混沌系统中最大李雅普诺夫指数λ＞0，表示系统既不会稳定在不动点，也不存在稳定的周期解，同时也不会发散，系统进入混沌。求得各监测点脉动信号的最大李雅普诺夫指数均大于0，分别为0.000 23、0.000 39、0.000 24、0.000 086、0.001 506、0.002 235，因此该双向流道泵机组压力脉动信号具有混沌特性。

4.3 关联维分析

关联维数作为分形维数的一种，能描述时间序列相空间中奇异吸引子的维数，可由时间序列直接得到［28］。关联维数度量了重构相空间的向量距离随超球半径变化的速率，也度量了系统内部结构复杂程度。采用G-P 算法计算关联维数，关联积分C（r）定义如下：

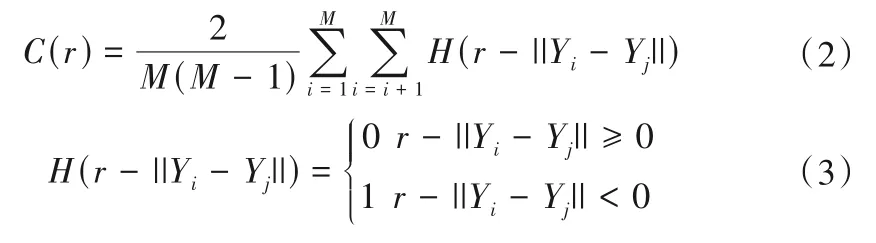
式中：r为相空间中超球体半径；Yi为重构相空间中的向量。

作出关联积分曲线lnr～lnC（r），对曲线上的直线区域拟合得到关联曲线。逐渐增加嵌入维数m直至其斜率不发生明显变化，即呈现饱和趋势，对此时的斜率进行拟合即得到关联维数D，此时的m为最优嵌入维数。

图6 为设计工况下P3、P6、P9、P12、P15、P18号监测点嵌入维数从1递增到30的关联积分曲线图，拟合即得关联维数D，分别为2.7、2.08、3.3、1.96、2.02、1.96。由图6 可知，随着嵌入维数m的增大，关联维数D也相应增大，直至趋于饱和，近乎不变，这是混沌时间序列的特征，设计工况下各监测点压力脉动信号的混沌特性得以验证。叶轮出口P9点处监测点的关联维数最大，出水喇叭口P18点处关联维数最小。结合图4 来看，关联维数大小与压力脉动振幅变化大小相对应，振幅变化越大，关联维数越大；振幅变化越小，关联维数越小。

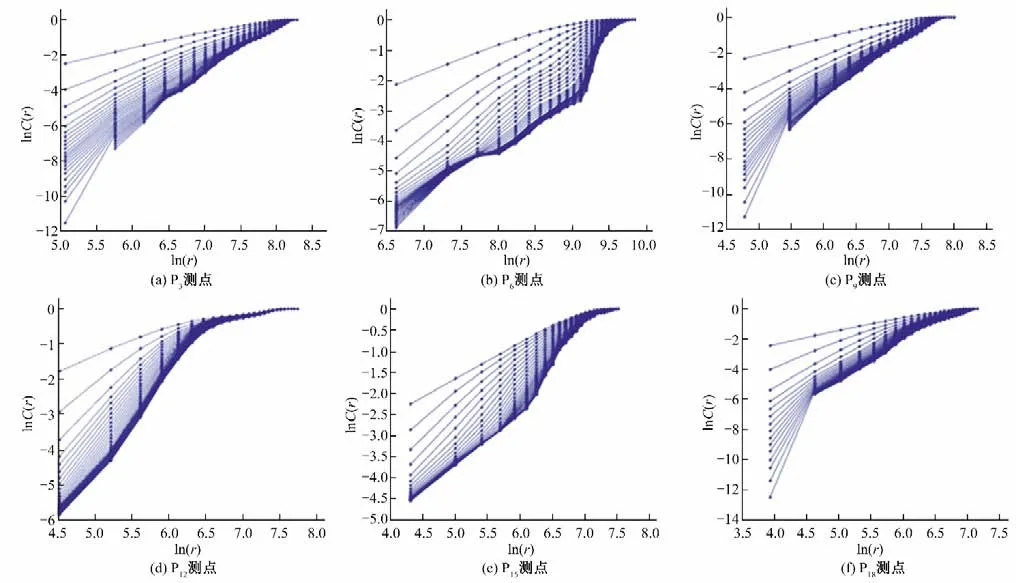
图6 各测点关联积分曲线图Fig.6 Correlation integral curve of each measuring point

4.4 分形标度分析

利用去倾扰动分析法（DFA）［26］对分形标度进行求值。对压力脉动时间序列｛x（t）｝求平均值xˉ，分别与均值作差，累加得序列y（k）：

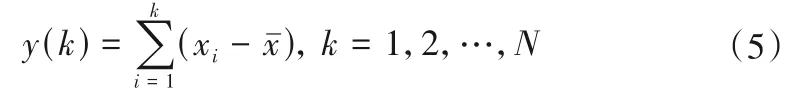
将y（k）平均分为l份的新序列，每一份的长度即为n=N/l。通过最小二乘法对新序列进行拟合，求得每个子序列的拟合函数yn（k）后，求取y（k）与yn（k）差值的均方根F（n）：

选取每个监测点的后800个数据，取100以内800的因数得n=5，8，10，16，20，25，32，40，50，80，100，进行lgn-lgF（n）曲线图的绘制如图7 所示，拟合的对数曲线的斜率即为相应的时间序列对应的分形标度值。

由图7 可知，随着lgn的增大，lgF（n）也随之增大，拟合曲线的斜率逐渐减小，求得的相应的时间序列对应的分形标度值分别为1.683 8、0.722 1、2.195 1、1.957 2、2.546 4、1.842 0，从数据上可以看出分形标度值均大于0，可知每个时间序列均为混沌时间序列。监测点P6分形标度值最接近0，最接近临界混沌状态；监测点P15分形标度值最大，代表在此情况下混沌特性最强。

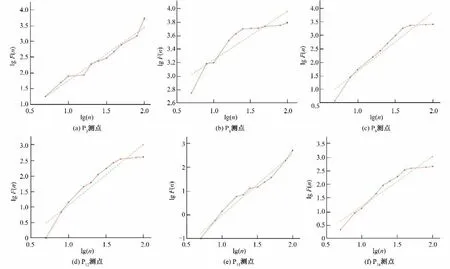
图7 设计工况F（n）-lg n曲线图Fig 7 Diagramlog F（n）-lg n of design condition

5 结 论

（1）数模得到的外特性曲线与试验外特性曲线变化趋势一致，表明计算结果可靠。

（2）进水喇叭口处水流、速度方向发生变化，压力脉动波形较乱，无明显的周期性；叶轮进口受叶轮转动影响，压力脉动周期性规律明显；叶轮出口受动静干涉作用，压力脉动波形复杂；导叶出口、出水喇叭口距叶轮较远，压力脉动规律不明显，但幅值较高。

（3）各测点最大李雅普诺夫指数均大于0，表明双向流道泵站压力脉动时域信号具有混沌特性，可用混沌理论进行分析研究。

（4）随着嵌入维数的增加，关联维数呈现饱和的趋势，进一步证明压力脉动时域信号具有混沌特性，计算得到的时间序列均为混沌时间序列。P9测点振幅变化最大，关联维数最大；P18测点振幅变化最小，关联维数最小；各监测点关联维数大小与压力脉动振幅变化大小相对应。

（5）各时间序列对应的分形标度值均大于0，监测点P6分形标度值最接近0，表明该点最接近临界混沌状态；监测点P15分形标度值最大，表明该点下混沌特性最强。混沌理论为分析泵站的压力脉动提供了一种新方法。