素养立意下一道视角极值题的溯源、破解与思考

张志刚

(山东省宁阳县复圣中学 271400)

1 题目呈现

题目(2022年1月广东省华附、省实、广雅、深中高三四校联考第7题)在足球比赛中，球员在对方球门前的不同位置起脚对球门的威胁是不同的,出球点对球门的张角越大， 射门的命中率就越高.如图1为室内5人制足球场示意图，设球场(矩形)长BC大约为40米，宽AB大约为20米，球门长PQ大约为4米.在某场比赛中有一位球员欲在边线BC上某点M处射门(假设球贴地直线运行)，为使∠PMQ最大，则BM大约是( ).(精确到1米)

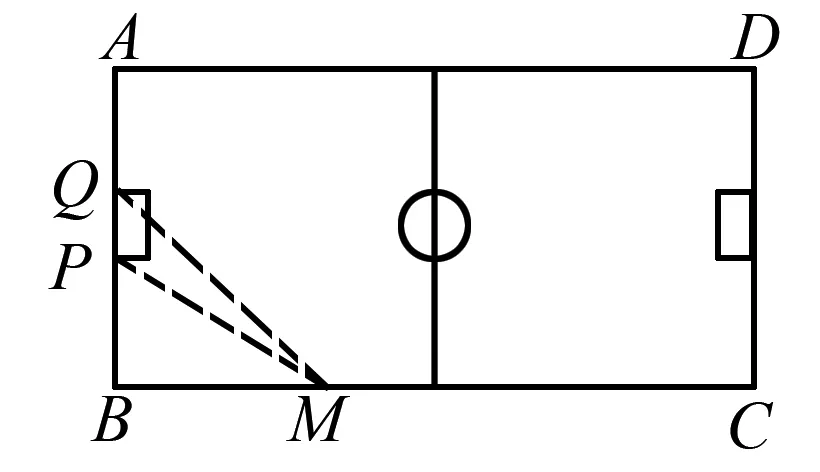
图1

A.8米 B.9米 C.10米 D.11米

本题通过设置鲜活的生活情境，考查一类最大张角问题，重点考查直观想象、数学建模、数学运算、逻辑推理等核心素养，内蕴丰富，具有较高的挖掘价值.

2 命制背景

2.1 问题探源

通过对典型习题的深度挖掘，有利于我们发现问题的内涵和本质，“揭秘”题目背后的故事与历史渊源，概括归纳深藏其中的思维主线，以此为中心推而广之，可以收到以一敌百的良好成效.本题源于历史上经典的米勒问题.1471年，德国数学家、天文学家米勒(Johannes,miller)向诺德尔(Chri-stian,roder)教授提出了如下有趣的问题:在地球表面的什么部位，一根垂直的悬杆呈现最长(即可视角最大)？上述最大视角问题因米勒首先提出，故称之为米勒问题.米勒问题广泛分布于各种实际问题，例如探求欣赏一幅画的最佳角度、足球比赛最佳射门点等，成为世界数学史上100个著名极值问题的第一个极值问题.历史上的米勒问题所涉及的范围是三维空间.作为实际问题，我们首先抽象出数学模型.如图2所示，相对于悬杆而言，地球的体积是相当大的，我们可视地球表面为平面，为了简化模型，同时忽略观察者身高的影响，即观察者的身高视为0，且悬杆在地面上的投影也为0，因为悬杆垂直于地面，所以到点O距离相同的点所得可视角相同.

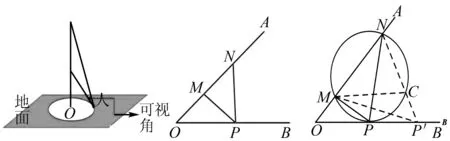
图2 图3 图4

2.2 模型概括

将上述问题一般化：如图3，设M,N是角∠AOB的一边OA上的两点，试在边OB上找一点P，使∠MPN最大.

对于上述问题，我们有如下定理：

米勒定理设M,N是角∠AOB的一边OA上的两点，点P是射线OB上异于点O的一动点，则当且仅当△MNP的外接圆与射线OB相切于点P时，∠MPN最大.

证明如图4，在射线上任取异于点P的一点P′，连接MP′,NP′,NP′与圆相交于点C.易知∠MCN>∠NP′M.又因为∠MCN=∠MPN,所以∠MPN>∠MP′N,得证.

2.3 教材链接

普通高中课程标准试验教科书《数学必修5》(人民教育出版社2007年1月第3版，A版)第101页习题3.4B组第2题：如图5，树顶A离地面am,树上另一点B离地面bm,在离地面cm的C处看此树，离此树多远时视角最大？

图5 图6

3 问题解答

思路1 几何视角，由圆的几何性质探求张角最大值.

解法1如图6所示，易知无论点M是前行还是后退到点M′，过点P,Q,M′的圆必与直线BC相交，此时∠PM′Q必小于圆内的角∠PMQ.

思路2代数视角，由探求张角的三角函数值的最值求张角最大值.

解法2 如图6所示，PB=8，QB=12，设BM=x(0≤x≤40).

所以tan∠PMQ=tan(∠QMB-∠PMB)

本题还可讨论∠PMQ的正弦或余弦的最值进行求解，不再赘述.

4 模型应用

以米勒问题为背景的最大张角问题在历年高考中屡见不鲜，经久不衰，现枚举几例.

例1(1986年高考全国卷理科第5题)如图7，在平面直角坐标系中，在y轴正半轴(坐标原点除外)上给定两定点A,B，试在x轴正半轴(坐标原点除外)上求一点C，使∠ACB取得最大值.

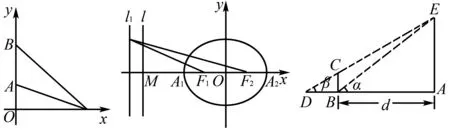
图7 图8 图9

例2(2005年高考浙江卷理科第17题)如图8，已知椭圆的中心在坐标原点，焦点F1,F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，|MA1|∶|A1F1|=2∶1.

(1)求椭圆的方程；

(2)若直线l1：x=m(|m|>1)，P为l1上的动点，使∠F1PF2最大的点P记为Q，求点Q的坐标(用m表示).

例3(2010年高考江苏卷第17题)某兴趣小组测量电视塔AE的高度H(单位m)，如图9所示，垂直放置的标杆BC高度h=4 m，仰角∠ABE=α，∠ADE=β.

(1)该小组已经测得一组α,β的值，tanα=1.24，tanβ=1.20，请据此算出H的值；

(2)该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离d(单位m)，使α与β之差较大，可以提高测量精确度，若电视塔实际高度为125 m，问d为多少时，α-β最大.

限于篇幅，以下仅给出例3(2)的解答：

解法1 由题设知d=AB，得

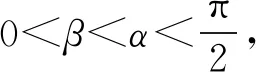
解法2由题设知α-β=∠DEB.

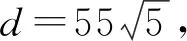
特别值得关注的是，近年来，米勒问题在竞赛数学中也频频亮相，需要引起足够的重视.

例4(2004年全国高中数学联赛第12题)在平面直角坐标系xOy中，给定点M(-1,2),N(1,4)，点P在x轴上移动，当∠MPN取最大值时，点P的横坐标为____.

解析设直线MN与x轴交于点Q，易得Q(-3,0)，圆H过点M,N且与x轴相切于点P，则点P即为所求.

由切割线定理,得

所以|PQ|=4.

易得P(1,0)或P′(-7,0).

而∠MPN>∠MP′N，故点P的横坐标为1.

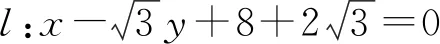
则∠APF1=∠AF2P，|AP|2=|AF1|·|AF2|.

又由△APF1∽△APF2，可得

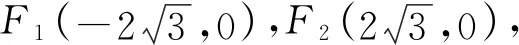
解析由已知得A(a,0)，F1(-1,0),F2(1,0).

首先考虑点P在x轴上方的情形.

设P(a,t)(t>0)，则

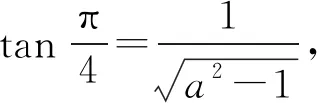
解得a2=2，即t=1.

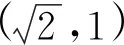
评注例6中，点P在x轴上方时，其位置可由米勒定理直接确定：经过点F1,F2且与直线l相切的圆的切点，由切割线定理，可知 |AP|2=|AF1|·|AF2|.

通过以上分析可以看出，以米勒问题为背景命制的试题在高考、竞赛和模拟试题中频频亮相，常常以解析几何、平面几何和实际应用为载体进行考查.若能突破思维瓶颈，从题设中挖掘出隐含其中的米勒问题模型，并能直接运用米勒定理解题，无疑会降低思维难度、大幅减少运算量，加快解题进程，促使问题顺利解决.