整体法在高中物理力学解题中的应用
马向京
(安徽省马鞍山市红星中学 243011)
就高中阶段的物理力学相关知识而言,其整个知识体系都比较繁杂,因此,学生在应对该类题型解答的时候,就需具备明确明晰的思路进行解题,将整体法运用于力学解题当中,其既是相对全面的一种解题方法,也是一种逻辑明晰的解题思路,这不仅能够使学生更加准确的把握住力学题的解题入手点,而且还可以使学生在力学题的解答当中,避免出现错误的思维,从而使学生在面对力学题时的解答效率得到切实提高.就整体法来说,通常就是让学生在物理学科的实际学习中,站在整体化角度,对与物理相关的运动规律实施观察,以整理出物体之间的正关联及整合,以此对相关力学问题实施综合、全面的解决.同时,高中物理的力学解题过程中运用整体法,不仅能防止学生由于力学知识的复杂性,无法有效解题,而且还可以促进物体受力的整个过程实现简化,并站在相应的高度,提取力学试题当中的关键信息,以此使学生准确掌握有关内容的同时,实现高效率的力学试题解答.
1 整体法概述
在高中物理中的力学解题当中应用整体法,通常指对力学题实施系统化或全过程的分析以及研究的一种方法.就力学而言,其则是把各个物体看作为整体,以其为对象,开展受力分析,但是,其更多的对整体之外的相关物体所做出的力加以分析,而没有考虑物体内部的作用力.整体则是将物体整体系统当做研究的对象,依据整个过程或整体,准确的把控物理现象中的具体规律,这通常是将有相互依赖、相互联系、相互作用、相互制约的多种状态、多个物体等组合成融洽且有研究价值的思维形式.对于整体思维而言,其属于综合性思维,是高度综合的多种思维,具有较强的理论性与应用价值.
整体法是物理知识学习的常用方法,特别是高中物理的力学解题过程中,整体法的运用更加常见.对于力学内容而言,其具有较强的综合性,且涉猎的范围也比较广,再加上该部分内容的逻辑性比较强,因此,教师与学生需注重力学相关内容的学习与掌握.
2 整体法在力学解题中应用的重要性及其注意内容
2.1 整体法在力学解题中应用的重要性
高中阶段物理内容中,力学的受力分析一般是学生最难以理解与掌握的内容.在解答力学试题时,学生一般只是会对个体问题进行分析,但却没有注意到其中存在的变量,再加上学生在力学题的解答时,较为随意、松散,在分析物体具体受力时也不够全面,这就容易造成内容遗漏.同时,学生解题时碰到与连接体有关的问题时,大部分学生更多会运用整体法以及隔离法,并把与其有关的力学题之间的连接作为整体,在分析受力的时候,也是对其整体开展分析,这种情况下,学生解答相关力学题的时候,就能避开复杂的步骤,降低解题的实际难度,最终实现力学题的解答准确率提高.整体法、隔离法彼此的作用是相互关联的,都对学生的解题具有显著的帮助,鉴于此,学生在对力学题进行解答前,明确整体法、隔离法彼此存有的差异,并清晰的知道在遇到哪类题型的时候,选择哪种方法,并明确了解到整体法的运用优势.通过相应的分析,不论是解题准确与正确的效率,还是学生自身具备的思维方式,都能体现出整体法在力学题解答中的重要性,并实现力学题的高效化解答.
2.2 整体法在力学解题中应用的注意内容
首先,注重学生的整体思维培养.许多学生通过整体法进行物理问题解决时,因为对整体法缺乏认识,并影响到解题效果提升.因此,在整体法运用时,需注重整体思维的培养,这也是高效解题的基础.教师在引导学生对相关物理知识实施归纳总结时,可通过思维导图,帮助学生构建知识体系,以促使学生充分掌握相关物理知识的相互关系,并促进学生的物理思维以及整体意识提升.
其次,注重空间想象力培养.物理教学中,整体法的有效运用,通常需学生充分理解物理题目,并绘制图形进行解题,以促使学生的空间想象力得到显著提升.因此,在整体法应用之前,物理教师需对学生自身的物理思维进行锻炼,引导学生想象物体的运行与受力,并经过绘图的形式,促进学生空间想象精准性的提高,从而使学生能更好的运用整体法进行解题.
3 整体法在高中物理力学解题中的应用
3.1 运动过程类题型中整体法应用
高中物理的教学中,需注重学生充分掌握分析物体实际运动状况的技巧与能力,牢记物体在具体运动状态下所产生的变化,及其变化时受到的力的作用.物体的运动过程通常能分成单个物体进行单段运动以及多段运动、多个物体进行多段运动.通常来说,在对物体运动过程中的多个物体的实际受力状况进行分析时,首先,需把多个物体分成不同局部,如果各物体的加速度相同,且各物体之间不需要作用力的时候,就能将其看作为整体,对整体的受力的合力进行分析,运用牛顿第二定律,对加速度进行求取.
3.2 相互作用类题型中整体法应用
物理力学的具体教学当中,其彼此的互相作用一般有弹力、摩擦力、重力等,面对连接体相互作用的相关问题中,运用整体法就显得极其重要.例如,木块1与木块2,其均处于光滑水平面,质量分别是m与M,两个木块使用一条细绳进行连接,水平力F应用到木块2上,让两个木块进行加速运动,那么,两个木块之间轻绳的实际张力是?此时,物理教师可应用整体法对其加以分析,把两个木块当成为一个整体,然后,对木块1的具体受力状况进行单独分析,由此可得张力.
3.3 力学综合类题型中整体法应用
高中物理的力学题中,其类型最多的就是综合题型的分析与解答,在对该类型题解答的时候,应用整体法,需充分关注到其中的条理分析,特别是力的分析与合力的分析,另外,涉及到正负数量或电荷量时,也需注重条理分析.例如,图1当中ab为2个带电体,其质量均通过m代表,已知a的电荷量为+2q,b的电荷量为-q,如果2个小球以绝缘线加以连接,并用长度一样的绝缘线,将a吊到天花板,电场的强度通过E进行代表,若a、b平衡的时候,2根线都位于拉直的状态,此时,a、b的竖直方向的夹角是什么关系?
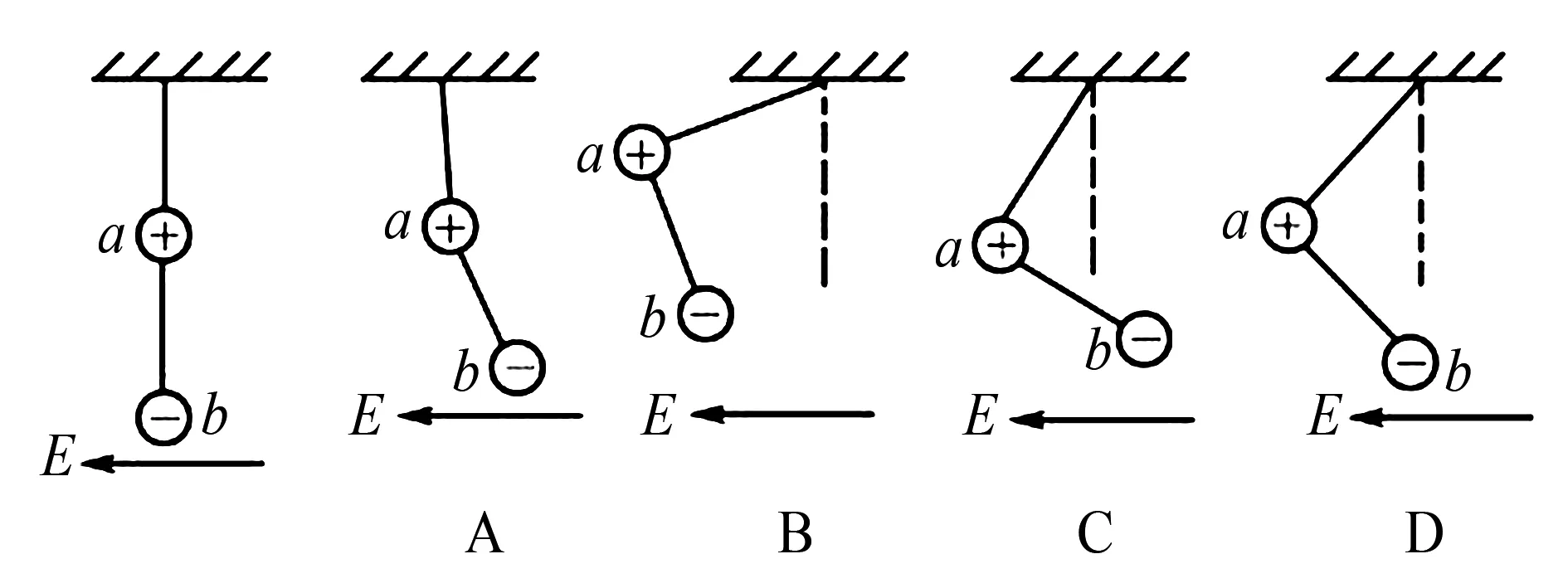
图1
通过整体法进行解题,可把a、b球当做一个整体,因为电荷数不同,a更多是正电数,因此偏左,具体的幅度可根据图1 中ab小球和竖直方的角幅度开展计算,因此,把a和竖直方向形成的夹角可设置成α,b和竖直方向形成的夹角设置成β,tanα=Eq/2mg,以计算出a的幅度,tanβ=Eq/mg计算从b的幅度,因此α<β,也就是a竖直方向夹角比b竖直方向的夹角大,因此,C是正确的.
3.4 物体平衡题型中整体法应用
高中物理的知识当中,平衡问题作为力学题解答的基础,因此,其占据了很大的比重,对学生分析物体受力的能力是极大的考验.对于平衡类问题而言,其通常分成两种,主要是单个物体、连接体当中各个物体之间的受力分析.就单个物体来说,对其平衡问题分析相对简单,主要是三个力平衡、三个以上的力平衡、动态平衡,而连接体平衡分析通常有着较高的难度,需通过整体法对物体的实际受力情况进行分析.如图2所示,倾角是α的粗糙的斜劈置于粗糙水平面,物体a置于斜面上,轻质的细线一侧固定于物体a上,另一侧绕过光滑滑轮固定于c处,滑轮2下可悬挂个物体b,系统位于静止的状态,现在将固定的点c逐渐向左缓慢的移动一点,就会发现a和斜劈处于静止,在该过程当中,以下说法正确的为( ).

图2
A.斜劈对于地面造成的压力不变
B.细线对于物体a产生的拉力增大
C.细线对于滑轮2的作用不变
D.地面对于斜劈摩擦力明显增大
解析对滑轮与物体b的受力进行分析,依据平衡条件对细线的拉力实际变化状况进行求解;对滑轮2实施受力分析,依据平衡条件对细线对于滑轮2作用力实施分析;对斜劈、物体a、物体b的受力整体情况进行分析,依据平衡条件,对整体和地面的静摩擦力与弹力状况实施求解,答案:AC.
综上所述,整体法运用于力学题的解答中,不仅能节省具体解题时间,而且还能促进解题准确率提升.同时,力学试题的具体解答中,整体法运用,还能对思维实施有效整合,并通过整体法进行力学问题的解答,不仅能实现解题效率的切实提高,而且还能锻炼学生的综合性思维,从而使解题水平提高.

