关于多边形数的几个结论
甘志国
(北京市丰台二中 100071)
1 关于多边形数的4道考题
题1 (2009年高考湖北卷文科、理科第10题)古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( ).

图1
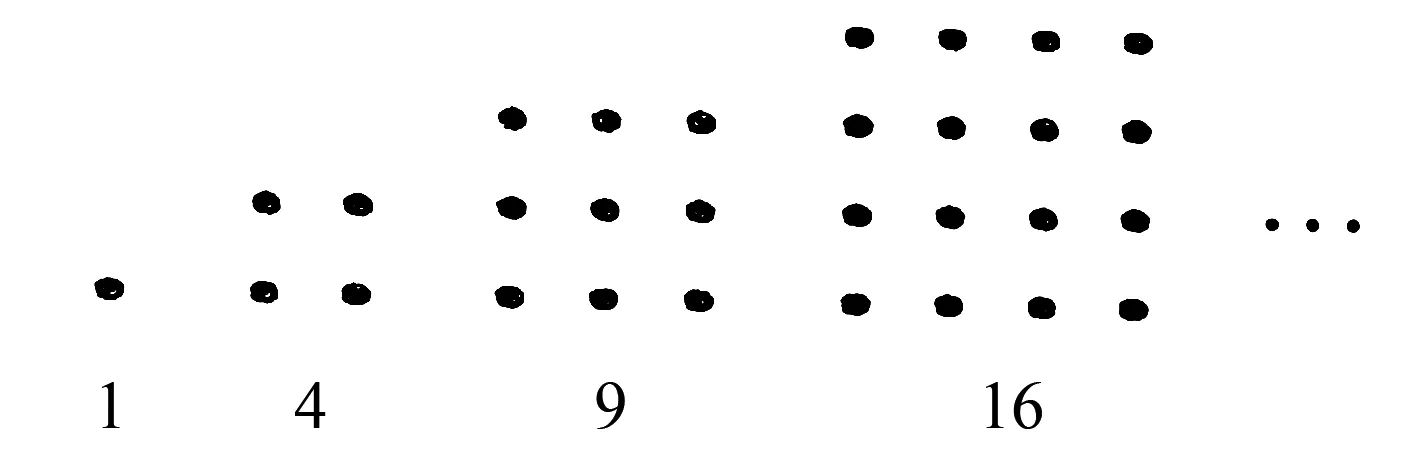
图2
A.289 B.1024 C.1225 D.1378
答案C.
注题1出自当时的教材普通高中课程标准实验教科书《数学5·必修·A版》(人民教育出版社,2007年第3版)第28页的相关叙述,及现在使用的教材普通高中教科书《数学·选择性必修·第二册·A版》(人民教育出版社,2020)第9页第5题.

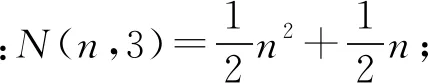
正方形数:N(n,4)=n2;

六边形数:N(n,6)=2n2-n;…
可以推测N(n,k)的表达式,由此计算N(10,24)=____.
解析本题主要考查考生应用观察、猜想、验证等步骤进行合情推理的解题能力.
由所给的四个等式可猜测
N(n,k)=akn2+bkn(k≥3),


①
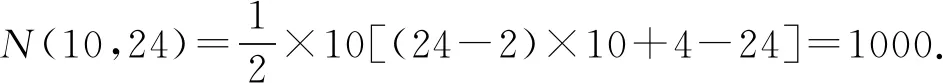
题3 (2012年高考湖北卷文科第17题)传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图1所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:
(1)b2 012是数列{an}中的第____项;
(2)b2k-1=____.(用k表示)

题4(2001年上海交通大学联读班数学试题第6题)有一盒大小相同的小球,既可将它们排成正方形,又可将它们排成正三角形,已知正三角形每边比正方形每边多2个小球,则这盒小球的个数为____.
解析设正方形每边是n个小球,得1+2+3+…+(n+2)=n2,进而可得n=6,n2=36.
2 关于多边形数的几个结论
下面用N(n,k)表示第n(n∈N*)个k(k∈N,k≥3)边形数.
定理1 (1)三角形数的2倍的个位数字是0,2,或6;正方形数的个位数字不是2,3,7,8;
(2)连续求三角形数的各位数字之和的最后结果是0,1,3,或6.
证明(1)当n=1,2,3,…,10时,可得三角形数的2倍,即n(n+1)的个位数字依次是2,6,2,0,0,2,6,2,0,0;
当m=1,2,3,…,10时,可得正方形数m2的个位数字依次是1,4,9,6,5,6,9,4,1,0.从而可得欲证结论成立.
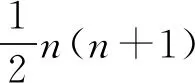
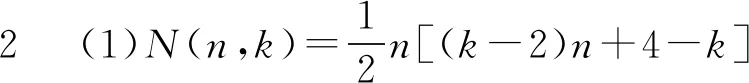
(2)8(k-2)·N(n,k)+(k-4)2
=[2(k-2)n-(k-4)]2,
证明(1)著作[4]第225页的表75即下面的表1:

表1
由表1的各行,可得

第n个正方形数N(n,4)=1+3+5+…+(2n-1)=n2;

第n个六边形数N(n,6)=1+5+9+…+(4n-3)=n(2n-1);

进而可得第n(n∈N*)个k(k∈N,k≥3)边形数
(2)由结论(1)可得结论(2)的第一个等式成立;再由2(k-2)n-(k-4)=(2n-1)k+4-4n≥(2n-1)·3+4-4n=2n+1>0,可得结论(2)的第二个等式也成立.
注用定理1及定理2(2)可判断一个数是否为k(k∈N,k≥3;k已知)边形数:
①小学生即可用排除法给出题1的简解:
由定理1(1)的第一个结论可排除选项A,B;由第二个结论可排除选项D.故选C.
②我们用定理2(2)来判断一个数是否为k(k∈N,k≥3,k已知)边形数:
先看55是不是七边形数?

再看46是不是七边形数?

又看33是不是七边形数?
因为8(7-2)×33+(7-4)2=1329=(36.4554…)2不是整数,所以33不是七边形数.
定理3 不是1的k+1(k∈N,k≥3)边形数均可表示成一个三角形数与一个k边形数之和:N(n+1,k+1)=N(n,3)+N(n+1,k)(n,k∈N*,k≥3).
推论1不是1的正方形数均可表示成两个三角形数之和:N(n+1,4)=N(n,3)+N(n+1,3)(n∈N*).
定理4 (1)前n个正整数的立方和是从小到大的第n个三角形数的平方:13+23+…+n3=[N(n,3)]2(n∈N*);
(2)八个相同的三角形数与1的和是一个正方形数:8·N(n,3)+1=[N(2n+1,4)]2(n∈N*).

推论2(1)所有从小到大的既是三角形数又是正方形数的数组成的数列是
该数列{an}可由a1=1,a2=36,an+2=34an+1-an+2(n∈N*)确定;

该数列{an}可由a1=1,a2=210,an+2=194an+1-an+16(n∈N*)确定;

该数列{an}可由a1=1,a2=9801,an+2=9602an+1-an+200(n∈N*)确定;

该数列{an}可由a1=1,a2=1225,an+2=1154an+1-an+72(n∈N*)确定;
(5)所有从小到大的既是五边形数又是六边形数的数组成的数列是
该数列{an}可由a1=1,a2=40755,an+2=37634an+1-an+3136(n∈N*)确定;
(6)所有从小到大的第n个六边形数即所有从小到大的第2n-1个三角形数,所以既是三角形数又是六边形数的数组成的数列是{n(2n-1)},
该数列{an}可由a1=1,an+1=an+4n+1(n∈N*)确定.
证明用定理5来证.
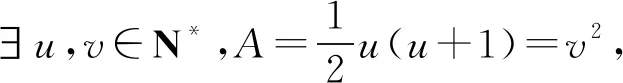
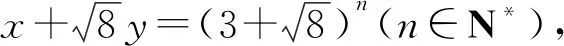
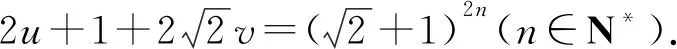
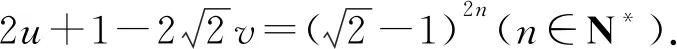


可得(6y-1)2-3(2x+1)2=-2.



从而可得欲证结论成立.

进而可得(6v-1)2-24u2=1.


因而A=u2
从而可得欲证结论成立.
(4)同(1)可证.


所以,当n∈N*时,

从而可得欲证结论成立.

猜想若k,l,m∈N,3≤k

