基于自适应CYCBD和1.5维谱的滚动轴承故障特征提取方法*

朱战伟,何怡刚,宁暑光,王 涛

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

0 引 言

滚动轴承在机械的传动系统中扮演着重要的角色。为了确保设备工作的稳定性,对轴承进行状态监测及故障诊断有重要的意义。

然而,在轴承故障诊断中,故障特征的表征与提取制约着故障诊断准确性的提高。因此,对故障特征的提取方法进行研究有重要的应用价值[1]。

在滚动轴承振动信号的特征提取方法中,因具有良好的故障特征表征能力,时频分析方法得到了广泛的应用。在对信号进行时频分析时,往往需要通过对振动信号进行时频域处理,进而提取故障特征。但是在实际工况环境中,故障信号会混杂于背景噪声信号及轴、齿轮等运动部件产生的谐波干扰信号中,使得直接对振动信号进行特征提取的难度很大[2-4]。

设计滤波器对观测信号进行滤波,是一种有效分离故障特征信号的方法。基于此,ANTONI J[5]提出了Kurtogram算法,并使用该算法成功对信号进行了自适应滤波。WANG Lei等人[6]将滑动的窗口与双树复小波包变换引入到Kurtogram算法中,并基于双树复小波包变换滤除噪声,有效提高了算法的频带分割能力。

但由于Kurtogram算法采用固定频谱分割策略,可能会导致一些故障信息的丢失。

近年来,盲解卷积算法也在轴承等机械的故障诊断中得到了广泛应用。盲解卷积采用反向搜索有限脉冲响应(finite impulse response,FIR)滤波器,进而进行信号去噪的策略,旨在通过更新和获得滤波器系数的最佳组合,以此来消除信号传递路径的影响,并从含噪振动信号中恢复故障脉冲[7]。

最小熵反褶积(minimum entropy deconvolution,MED)是较早应用于工程领域的盲解卷积方法。由于其具有优异的提取周期脉冲能力,现已被成功用于齿轮故障和轴承故障检测中[8,9]。但是,MED可能收敛到偶然出现的单个脉冲,而非故障引起的周期性脉冲。

为了克服MED的缺点,MCDONALD G L等人[10]提出了相关峭度(correlated kurtosis,CK)指标,并通过用相关峭度替代峰度来计算最大相关峭度反卷积(maximum correlation kurtosis deconvolution,MCKD)。MCKD通过指定信号周期,可以从混杂强烈背景噪声的信号中提取出感兴趣的所有周期性成分,在旋转机械的故障诊断中表现良好[11]。

但是MCKD需要较多的输入参数,参数的选择对其性能有较大的影响,而且峭度只考虑了信号的稀疏性,忽略了轴承振动信号的统计特征。

旋转机械振动信号的统计特征呈现周期性变化,该特征可以描述为循环平稳过程(cyclostationary,CS)[12]。近年来,有学者将循环平稳指标引入反卷积框架,进而提出了最大二阶循环平稳盲卷积(CYCBD)[13]。

随着更多学者的关注,已有学者提出将CYCBD方法与快速迭代滤波分解相结合,在对轴承信号进行滤波分解的基础上,使用CYCBD算法进一步解混提取故障特征信号[14]。赵晓涛等人[15]使用CYCBD算法对轴承振动信号进行了降噪,通过包络谱分析识别故障的特征频率。然而,CYCBD方法的性能强烈依赖于循环频率选择的准确性,这限制了CYCBD在故障诊断方面的应用。虽然有学者提出了应用谐波积谱(harmonic product spectrum,HPS)[16]来估计循环频率,但是当某阶谐波分量为零时,会对估计准确性造成影响。所以针对循环频率的估计问题仍需要做进一步研究。

考虑到上述情况,笔者提出一种基于自适应CYCBD和1.5维谱的滚动轴承振动信号故障特征提取方法(算法)。

该算法以最大化加权谐波和为优化目标,在搜索的频率范围内,跟踪确定CYCBD的最优循环频率;通过参数优化后的CYCBD算法进行滤波,并结合1.5维谱抑制信号中的高斯白噪声,得到滚动轴承的故障特征信号。

1 基本原理

1.1 最大二阶循环平稳盲卷积

最大二阶循环平稳盲卷积(CYCBD)是一种盲卷积方法，其主要作用是从含噪信号x中恢复源信号s0，可将其描述为：

s=x*h=(s0*g)*h≈s0

(1)

式中：s—估计的源信号；x—观测信号；s0—待估计源信号；g—传递路径的脉冲响应函数；h—逆滤波器；*—卷积运算。

式(1)可用矩阵表示为：

(2)

式中：h—滤波器系数矩阵；L—信号s的点数；N—逆滤波器h的长度。

逆滤波器的求解过程可以表示为在条件约束下的优化问题。在CYCBD中，为了得到逆滤波器，引入了循环平稳性指标ICS2，该指标值越大，信号的周期性表现就越明显。

ICS2可以定义为：

(3)

式中：上标H—矩阵的共轭转置；RXWX—加权相关矩阵；RXX—相关矩阵。

其中，加权矩阵可以表示为：

(4)

(5)

(6)

(7)

|s|2=[|s[L-1]|2,…,|s[N-1]|2]Ts

(8)

式(4～8)中：W—加权矩阵；P[|s|2]—包含故障特征循环频率的矩阵；K—样本数；Ts—故障信号的周期。

其中，对于离散信号，循环频率定义为1/Ts。

CYCBD算法的最终求解过程可以描述为：

h0=arghmaxICS2

(9)

为了寻找最优滤波器h0，需要最大化式(3)。经过转化，最优滤波器可以通过搜索下式的最大特征值λ对应的特征向量来完成，即：

RXWXh=RXXhλ

(10)

其搜索过程描述如下：

(1)设置初始参数，包括循环频率、滤波器长度、最大迭代次数等；

(2)加载观测信号x，并计算相关矩阵RXX，加权相关矩阵RXWX；

(3)根据式(10)求解特征值问题，找到对应于最大λ的h；

(4)如果不满足收敛条件，重复步骤(2)。

1.2 循环频率的自适应估计

在周期性信号特征统计方面，CYCBD的循环平稳性指标ICS2具有优异表现，使CYCBD方法能较好地应用于轴承或齿轮等旋转机械的故障特征提取。

然而，在滚动轴承的特征提取中，为了使CYCBD算法能够滤除谐波信号和噪声信号，以得到轴承的故障特征信号，需要根据先验知识，预先设置合适的循环频率。

而在实际的轴承故障诊断中，真实故障特征频率可能会偏离理论故障特征频率，简单地将理论特征频率设置为循环频率，会导致CYCBD算法的滤波效果不佳。因此，为了提高算法的滤波能力，需要估计合适的循环频率。

谐波积谱(HPS)能有效提取声信号的基频，估计循环频率。但谐波积谱容易放大频率误差，出现倍频错误，使频率估计值偏大。

为了更精确地估计循环频率，笔者引入了一种谐波加权和指标来估计合适的循环频率。

谐波和的特点在于当频率和基频重合时，谐波和达到最大。笔者利用该特性对循环频率进行估计。同时，考虑到振动信号中常常混入高频噪声，以致高阶谐波失真，为了减小高次谐波对估计结果的影响，笔者引入了加权因子h。

谐波和函数可表述为：

(11)

式中：K—考虑的最大谐波次数；h—压缩因子，h=21-k；k—当前计算的谐波阶次。

笔者使用加权谐波和指标对循环频率α进行估计的过程，可描述为α=argf0max(H(f0))，就是将加权谐波和函数达到最大时的基准频率确定为循环频率。

另外，使用式(11)估计循环频率时，考虑到周期性的故障脉冲信号主要分布在较低的频率区域，而噪声的频率较高，谐波阶次过大会增加噪声干扰的影响，故笔者取最大谐波次数K为10。

1.3 1.5维谱

平稳振动信号x(t)三阶累积量的对角切片R3x(τ1,τ2)(τ1=τ2=τ)可以表示为：

R3x(τ,τ)=E{x(t)x(t+τ)x(t-τ)}

(12)

式中：E{·}—数学期望值。

平稳振动信号x(t)对角切片R3x(τ1,τ2)的一维傅里叶变换是1.5维谱B(ω)，可表示为：

(13)

2 故障特征提取

滚动轴承的采样振动信号是源信号与噪声的卷积混合,冲击特征微弱,CYCBD算法以二阶循环平稳指标构造滤波器,通过解卷积运算提取信号中的周期性脉冲成分。

经过对算法进行改进,使用CYCBD算法自适应构造最佳滤波器,使算法更适用于提取轴承的弱故障特征。

轴承振动信号在滤波后,信号中仍然有一些存在频率耦合关系的信号成分,利用1.5维谱对故障信号的包络信号进行分析,能够去除与故障特征无耦合关系的干扰谱线,同时有效抑制白噪声干扰。

综上所述,笔者结合自适应CYCBD和1.5维谱的优势,提出了基于自适应CYCBD和1.5维谱的滚动轴承故障特征提取方法。

其故障特征提取流程,如图1所示。

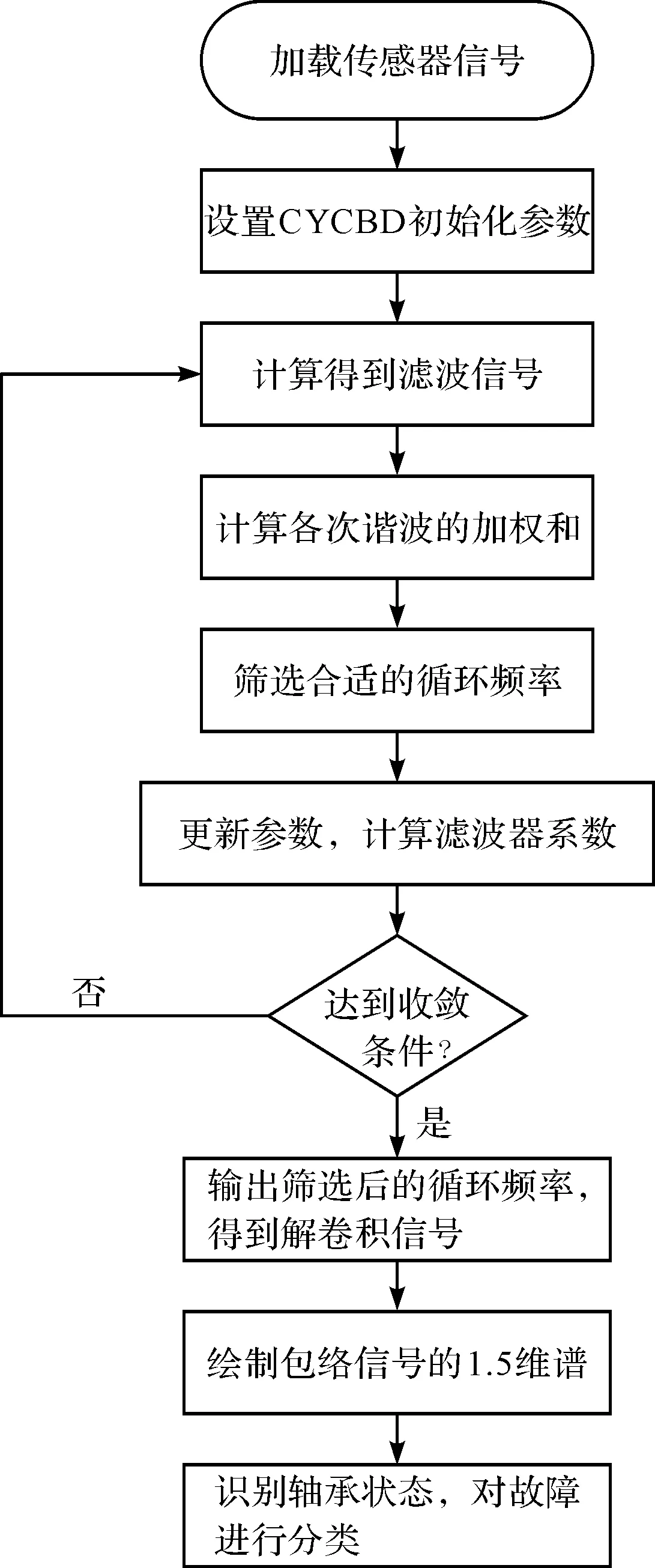
图1 基于CYCBD和1.5维谱的算法流程

基于自适应CYCBD和1.5维谱提取方法的具体实施过程如下:

(1)设置滤波器长度,最大迭代次数,收敛条件等初始化参数;

(2)在初始化条件下解卷积得到滤波信号;

(3)在搜索频率范围内,通过更新滤波器参数,搜索获得最大加权谐波和处的循环频率;

(4)通过最优循环频率计算解卷积信号;

(5)计算滤波后包络信号的1.5维谱,提取滚动轴承的故障特征,确定轴承的故障类型。

3 仿真信号分析

为了验证所提算法的有效性,笔者根据滚动轴承振动模型构建滚动轴承的内圈故障仿真信号。

仿真信号考虑了实际环境中的谐波干扰及噪声等成分,其振动信号描述如下:

y(t)=x(t)+b(t)+g(t)+n(t)

(14)

式中：x(t)—轴承缺陷激发的周期脉冲响应；b(t)—模拟外部振动或电磁干扰等产生的随机脉冲；g(t)—轴、齿轮等旋转运动产生的谐波干扰；n(t)—高斯白噪声。

其中，各部分信号的定义如下：

(15)

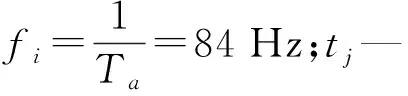
(16)

式中：η—系统结构衰减因子，η=1 500 rad/s；ε—随机脉冲传递路径衰减因子，ε=1 000 rad/s；fn—共振频率，fn=3 000 Hz；fr—轴承所在轴的旋转频率，fr=10 Hz。

笔者设置仿真信号的采样频率为25 kHz,采样时长为1 s。

仿真信号的时域波形和包络谱如图2所示。

图2 仿真信号

为了检验CYCBD方法的故障特征提取能力,笔者使用文献[13]中的CYCBD方法处理信号的包络谱(设置滤波器长度为40,循环频率分别为84 Hz、88 Hz)。

处理后信号的包络谱如图3所示。

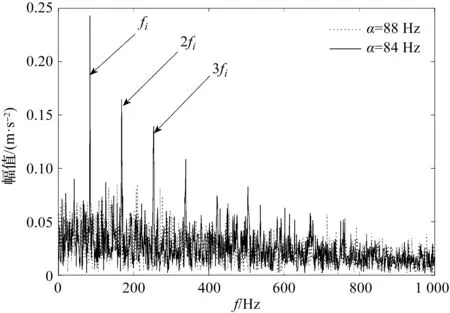
图3 CYCBD处理信号的包络谱

观察图3可知：当循环频率等于轴承内圈故障频率fi时，CYCBD算法有较强的故障频带定位能力；然而当循环频率α与故障频率fi偏移较大时，CYCBD不再有突出的故障表现能力。

笔者使用自适应CYCBD算法对仿真信号进行分析处理(滤波器长度取为40),其算法的迭代过程如图4所示。

图4 循环频率迭代曲线

观察图4可知：算法经过3次迭代，收敛到内圈故障特征频率fi，从仿真结果可以看出，加权谐波和方法可以快速有效地对循环频率进行估计。

算法处理后的信号时频域分析结果,如图5所示。

图5 该算法分析结果

对比图2(a)和图5(a)可知:信号经过处理后背景噪声受到较为明显的抑制,并且周期性脉冲的幅值得到了增强,在图5(a)中可以观察到周期性脉冲。

对解卷积信号进行包络分析，其包络谱见图5(b)。对比图2(b)和图5(b)可以看到：包络谱中故障频率周围的谐波频率成分得到明显的抑制，使故障频率fi及其倍频在频谱图中表现得更为清晰。

对包络信号进行1.5维谱处理,结果如图5(c)所示。对比图5(b)和图5(c)可以发现:1.5维谱进一步抑制了信号中的噪声干扰成分,使提取的信号特征成分更加清晰。因此,从仿真实验结果可以看出:在强噪声干扰及谐波存在的条件下,采用该方法可以有效地对较弱的周期性故障脉冲进行提取,从而对轴承故障进行诊断。

为了进一步分析算法的性能,笔者采用EMD算法处理仿真信号(并将其与该算法进行比较),EMD处理结果如图6所示。

图6 EMD分析信号结果

由于分解后的各阶模态分量包含不同的频率成分,为了筛选有效分量,笔者使用峭度准则对处理得到的本征模态函数IMF进行处理,选取峭度值大于3,且按降序排列的前4阶IMFs,处理得到其时域波形及其包络谱。

观察图6可以发现：IMF2分量的包络谱中包含较为清晰的故障频率。

IMF2分量包络谱如图7所示。

图7 IMF2包络谱

由图7可以发现：在IMF2的包络谱中出现了轴承内圈故障的特征频率及其3倍频,但是2倍频成分由于谐波干扰,不能在图中明显地表示出来,这造成了轴承状态诊断的困难。与笔者所提出的算法结果进行比较,说明了该方法在抑制噪声和提取故障特征方面有一定的优越性。

在前文中笔者使用该文所提算法对仿真信号进行了频谱分析,并与其他算法的分析结果进行了比较。

为了对算法的特征提取能力进行量化分析,笔者再次使用量化指标对各种算法进行评价。根据文献[17]对香农熵的研究,香农熵与信号中的周期性脉冲强度呈现负相关关系。笔者据此使用香农熵为指标,对算法提取轴承故障特征的能力进行评价[18]。

香农熵表达式如下:

(17)

式中：sh—香农熵；p(xi)—随机序列xi的概率分布；c—与单位相关的正数。

算法处理后信号的香农熵计算结果如表1所示。

表1 仿真信号处理结果分析

从表1结果可以看出:用笔者所提方法处理后,信号的香农熵远小于其他两种方法,说明该算法处理得到的信号中噪声成分含量较少,周期性的脉冲成分强度更高。

与前文的频谱分析结合,说明笔者所提算法有较好的抑制信号噪声,以及提取轴承信号中周期性故障脉冲的能力。

4 实验及数据分析

为了证明该自适应CYCBD方法在轴承故障诊断中的适用性,笔者使用西安交通大学XJTU-SY滚动轴承加速寿命实验数据[19]对此进行验证分析。

实验所用的轴承加速寿命测试平台如图8所示。

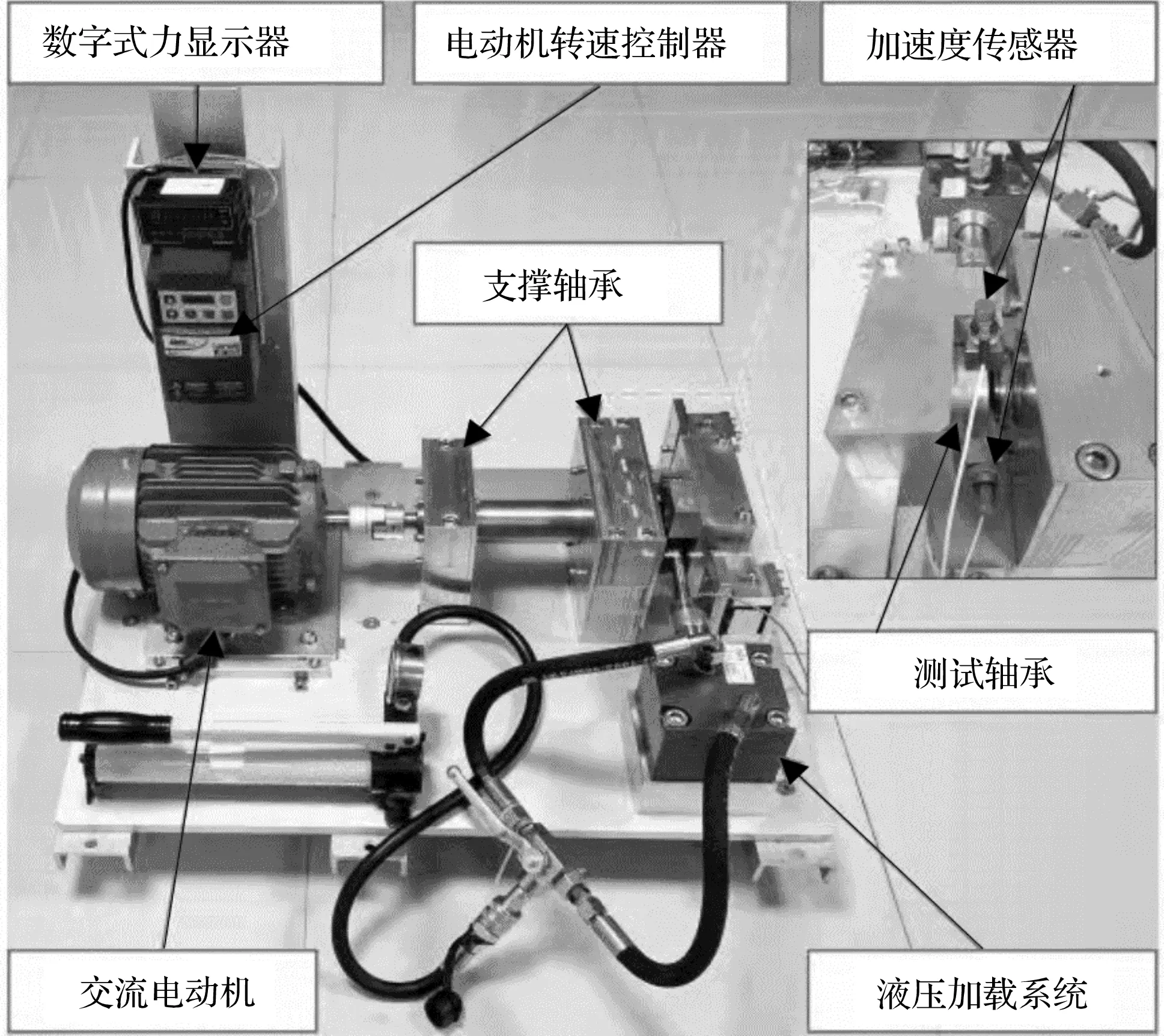
图8 轴承加速寿命测试平台

由图8可知：测试平台由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统、测试轴承、水平方向和垂直方向加速度传感器等组成。

实验中所采用的轴承为LDK UER204滚动轴承,其基本参数如表2所示。

表2 轴承基本参数

实验中,利用水平方向和竖直方向2个PCB 352C33加速度传感器,采集轴承在3组工况条件下运行时的振动信号。

实验中各工况条件设置如表3所示。

表3 实验工况

在每种工况下,分别对5个轴承进行了实验。实验设置的采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。

笔者取第1组工况下的轴承1测试数据,采集到的振动信号包含轴承的外圈故障振动信号;以Bearing1_1的第66组采样信号进行分析。

在采样信号中,水平方向采集到的振动信号时域波形,以及对振动信号进行包络分析得到的其包络谱,如图9所示。

图9 采样信号

由图9可以发现：虽然可以从原始信号的时域波形观察到较为突出的脉冲成分,但由于噪声和谐波的干扰,无法观察到明显的脉冲周期;在原始信号的包络谱中,观察到频率为108.1 Hz的谱线,其与计算得到的外圈故障理论频率107.9 Hz接近,且存在三倍频。

但在图9中,其二倍频程附近存在较多的杂频成分,不能判断是否存在二倍频,因此不能直接判断轴承的运行状态。

为了验证该改进算法的有效性,笔者拟先采用文献[13]中的参数化CYCBD算法对振动信号进行分析;设置滤波器长度为40,循环频率为实验轴承理论外圈故障频率107.9 Hz。

循环频率为107.9 Hz时,采用CYCBD算法处理得到的结果,即解卷积信号的时域波形和包络谱,如图10所示。

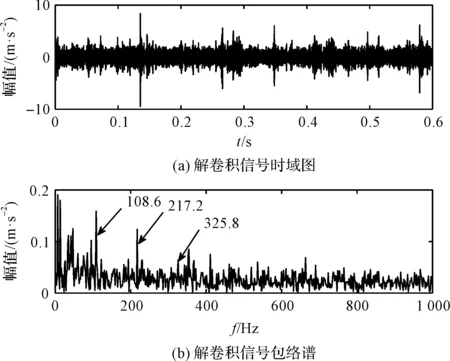
图10 循环频率107.9 Hz时CYCBD算法处理结果

从图10的时域波形图中可以看到：信号中的噪声成分得到了较好的抑制,周期性的脉冲成分得到了较大幅度的增强,可见算法处理后提高了信号的信噪比;在解卷积信号的包络谱中,观察到了108.6 Hz的谱线,其接近理论外圈故障频率,而且其二倍及三倍频也都出现在图10中。

笔者使用改进算法对振动信号进行处理,算法搜索循环频率的迭代过程,如图11所示。

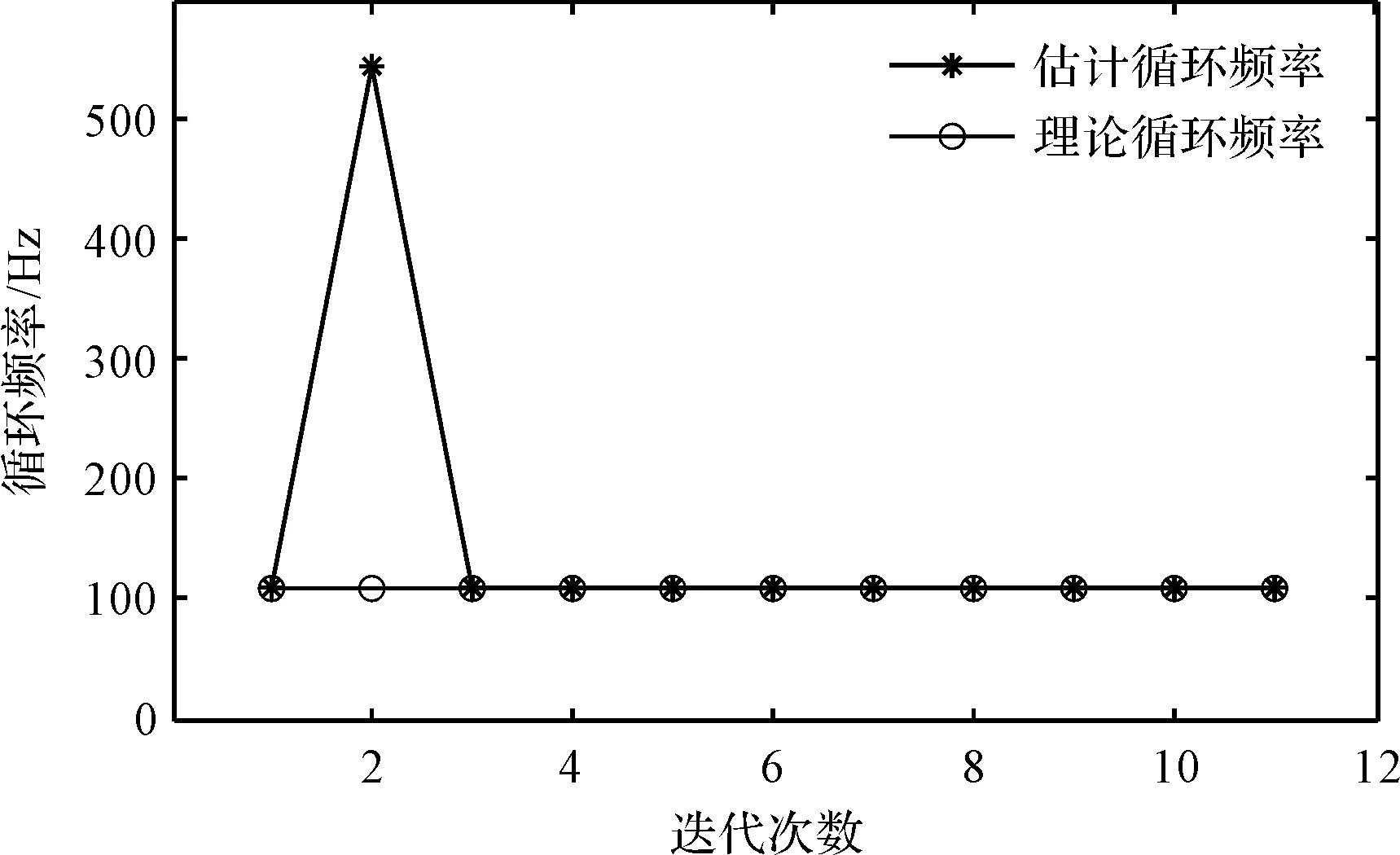
图11 算法迭代曲线

在图11中可以看到:经过3次迭代算法收敛,此时估计的循环频率为108.1 Hz,而理论循环频率为107.9 Hz。

由此可见,采用该算法能对循环频率进行快速搜索。

在该算法处理结果分析中,算法处理得到解卷积信号的时域波形和包络谱,如图12所示。

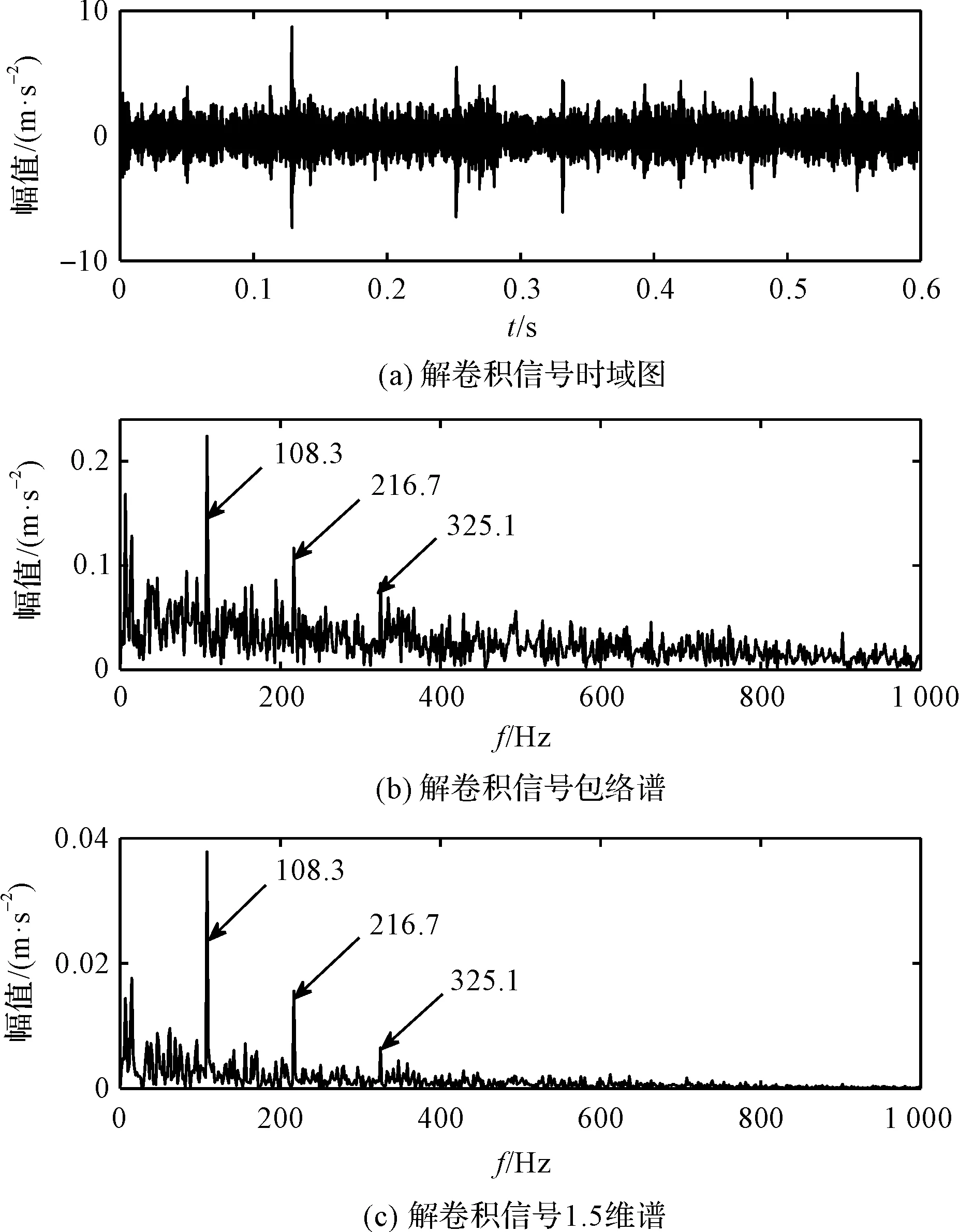
图12 该算法处理结果分析

笔者将解卷积信号的时域波形图与图10(a)进行比较可以发现:经该算法处理得到的信号与参数化CYCBD算法处理后的信号具有相似的周期性脉冲;

在图12(b)中可观察到：108.3 Hz的谱线及其倍频成分,与图10(b)进行比较,图12(b)中谐波频率成分受到了较大的抑制,故障特征频率表现更为清晰;

使用1.5维谱对包络信号进行分析,结果如图12(c)所示,从中可以看到:相比包络分析方法,1.5维谱方法可以较好抑制干扰成分,得到较为清晰的故障频率特征。

上述信号分析结果表明:在提取滚动轴承故障特征方面,该自适应CYCBD算法和1.5维谱方法具有较好的效果。

为了分析该算法的性能,笔者进一步采用EMD算法对轴承振动信号进行处理,并对结果进行对比,所得处理结果如图13所示。

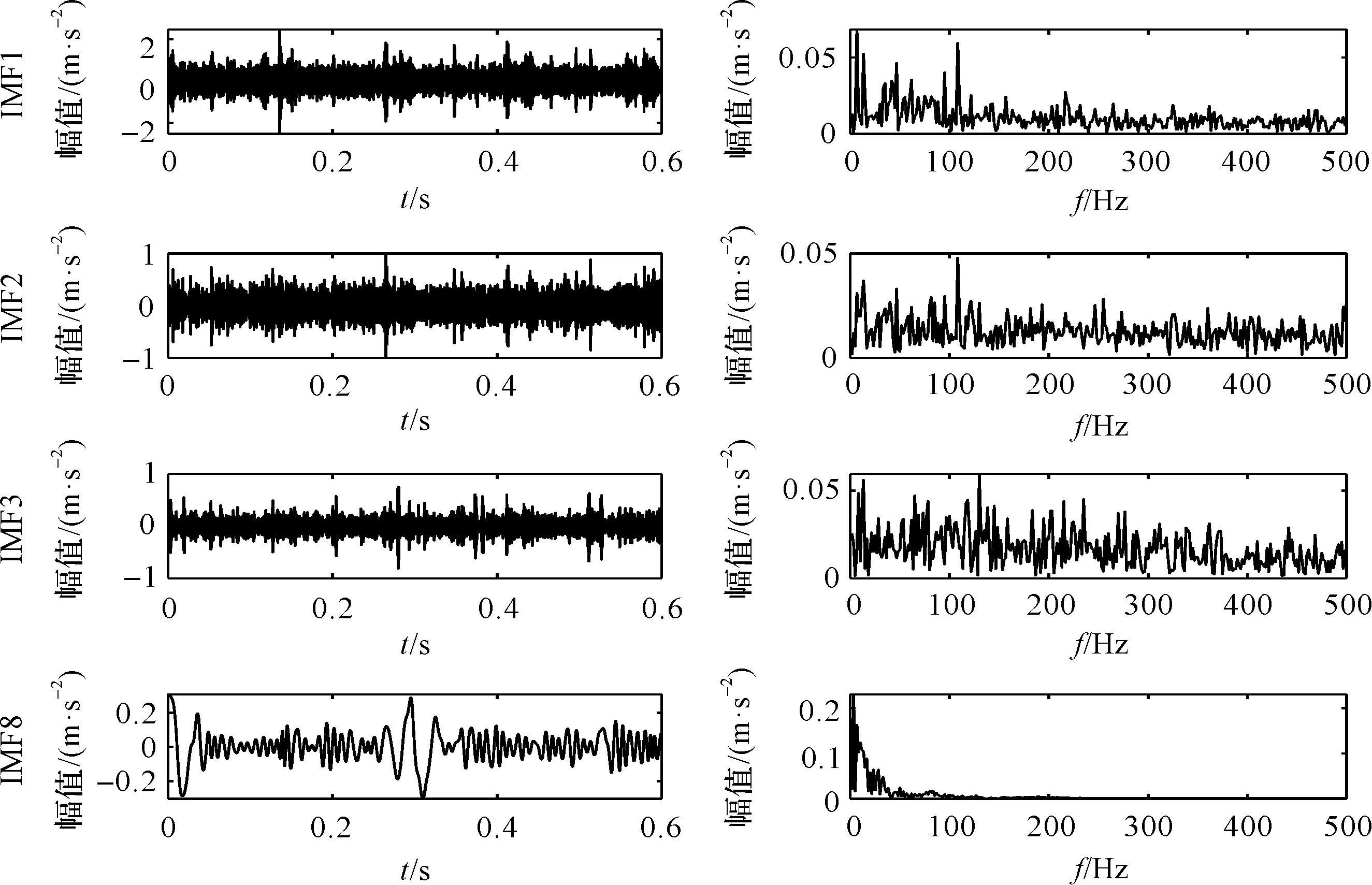
图13 EMD处理结果

图13展示了前4阶峭度最大的IMF时域波形及其包络谱。

由图13可以看出:前3阶分量保留了较多的频率成分,而且IMF1中保留了较多的故障信号成分。

笔者绘制IMF1的包络谱如图14所示。

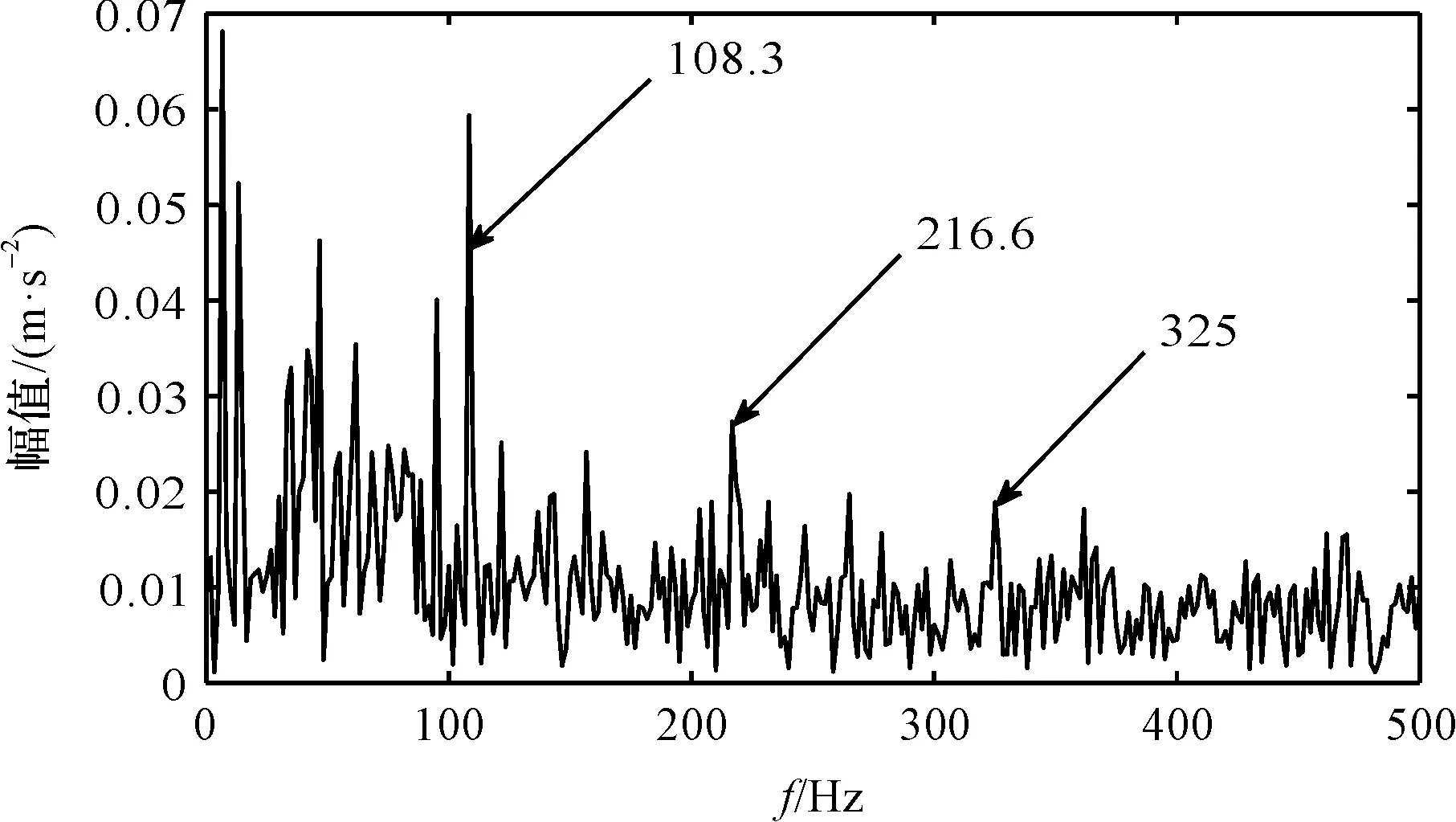
图14 IMF1包络谱

由图14可知:经过EMD算法处理在IMF1的包络谱中出现的故障特征频率及其倍频,发现其周围有较多干扰频率谱线。

对比图14和图12(b)可知:CYCBD算法可以增强故障特征,从而在包络谱中得到较为清晰的特征谱线,提高滚动轴承故障诊断的准确性。

因此,通过对不同算法分析结果的对比,说明了该方法在特征提取能力上具有一定的优越性。

与仿真信号相似,为分析该算法对实测信号特征的提取能力,笔者采用香农熵指标对算法处理结果进行分析,其结果如表4所示。

表4 实测信号处理结果分析

从表4可以看出:该算法处理后信号的香农熵小于其他两种方法,说明对于实测信号而言,相比于CYCBD方法和EMD方法,采用该算法有较强的抑制噪声和周期性故障脉冲提取能力。

5 结束语

为了对强背景噪声环境下的滚动轴承故障特征信号进行提取,笔者提出了一种基于自适应最大二阶循环平稳盲卷积(CYCBD)和1.5维谱的滚动轴承故障特征提取方法。

首先,使用加权谐波和指标改进CYCBD算法循环频率选取过程;然后,将CYCBD算法与1.5维谱相结合,并将其应用于滚动轴承的故障特征提取中。

理论仿真分析和实验验证结果表明:

(1)以加权谐波和指标对CYCBD的循环频率进行自适应选择,解决了人为选取参数的困难,使CYCBD算法更适用于实际的轴承故障特征提取;

(2)对于信噪比较低的轴承振动信号,采用CYCBD与1.5维谱相结合的方法,能够对振动信号起到较好的噪声抑制效果;

(3)在轴承的故障特征提取方面,与传统CYCBD方法和经典EMD方法相比,基于自适应CYCBD和1.5维谱的方法具有更为优秀的表现。

目前,笔者仅对单一故障情况下的轴承故障特征提取进行了研究,而在工程实际中,往往是多种故障同时存在。因此,在未来的工作中,笔者将进一步对轴承混合故障特征的提取进行研究。