基于改进蚁狮优化算法的柔性作业车间调度研究*
王彦杰,向凤红
(昆明理工大学 信息工程与自动化学院,云南 昆明 650000)
0 引 言
生产调度的出现,让人们脱离了原始的生产模式,解放了劳动力。但随着社会的发展,单一的生产调度模式,已经不符合人们日益增长的需求,需寻求更加有效的生产制造方式[1]。
柔性作业车间调度问题(FJSP)是传统的作业车间调度问题(job shop scheduling problem, JSP)的扩展[2]。柔性作业车间调度的不确定性和复杂性,适合现代多变、复杂的生产环境,同时也使得对该类问题的研究变得困难,促使越来越多的学者加入到调度生产模式研究中来。
目前,对于柔性作业车间调度问题的研究方法主要是利用智能算法模拟实际生产,寻求最好的调度方案。智能算法的出现为解决该问题提供了工具,极大程度上解决了复杂性强、问题规模大的FJSP问题。
SINGH M R等人[3]在传统粒子群算法中加入了量子行为策略,提出了一种混合量子行为粒子群算法,以此来求解柔性作业车间调度问题,但该算法对于初始种群的优化存在明显不足。乔兵等人[4]在遗传算法中设计了新的基因编码方式,对不合法基因进行了修复,求解了以最大最小完工时间为优化目标的柔性作业车间调度问题;但该算法优化后增加了完成加工的时间,且只针对不合法基因进行优化,有一定的局限性。贺仁杰等人[5]利用不同种群之间的进化方式以及调整参数设置,以此来推演优秀种群的演进过程,并且根据种群之间不同方式的演进过程和资源竞争,使种群之间的信息得以共享,从而推动了算法整体的进化,同时提出了通过知识型协同进化算法来求解柔性作业车间调度问题的方法;但该算法无法在大规模实例中进行准确优化,并且存在需要调整的参数多等问题。MASTROLOLLI M等人[6]利用禁忌搜索算法与新领域结构相结合的方式,增加了求解FJSP问题时算法搜索的效率与范围,避免了算法过早陷入局部最优;但该算法存在着运行时间过长、计算复杂度较高等不足。
上述文献说明,目前智能算法虽然已经得到了广泛的应用,但蚁狮算法求解FJSP问题的可行性国内外还无人能证明。同时针对传统蚁狮算法存在的不足之处,急需有一种计算复杂度低、求解进度高、调参少、能够解决实际大规模问题的改进蚁狮算法,以此来求解FJSP问题。
笔者尝试使用蚁狮优化[7](ALO)算法求解以最小最大完工时间为目标的FJSP问题。首先,提出基于混沌映射与竞标赛选择的混合策略,生成初始种群;其次,引入传统遗传算法中的最简单交叉变异策略,设计工序和机器加工选择的交叉变异策略;最后,利用Brandimarte基准算例进行实验对比分析,对该算法求解FJSP问题的有效性以及算法的性能进行验证。
1 柔性作业车间调度问题
1.1 问题描述
FJSP包括两个子问题:(1)对加工工序进行合理地机器分配;(2)对所选加工机器上进行不同加工工件的加工工序进行紧前紧后安排。
具体描述如下:柔性作业车间调度问题是n个工件(j1,j2,j3,…jn)可以在m台机器(m1,m2,m3,…mn)上加工,工件i(i=1,2,3,…,n)有qi道工序,每道工序所用的加工时间为t,允许工序可以在多个机器上进行加工操作,根据所选择的加工机器的不同,加工时间也不同。
调度问题研究的实质就是解决工件工序是否可以在某几台机器上加工,根据选择加工机器的不同,所产生的加工时间也不同;为实现最理想化的生产,对工件的工序进行安排以及选择合适的加工机器,是整个调度方案的重点。
在建立问题模型之前,需要对加工过程中进行一点条件约束,具体如下:
(1)机器在某时刻有且只有一个工件进行加工;
(2)工件工序在加工过程中,仅能选择一台机器进行加工操作;
(3)工件工序加工开始就不会停止,直到工件工序完成加工;
(4)待加工的工件,在选择加工时无主次之分,仅根据调度方案安排工件的加工;
(5)相同工件的不同工序需考虑加工先后顺序。
1.2 模型建立
为证明蚁狮算法求解柔性作业车间调度问题的有效性,笔者以最小最大完工时间(Cm)为目标,建立单目标柔性作业车间调度模型。
在其数学模型中,目标值为:
(1)
表示每个工件的每道工序加工开始就不能中断的为:
(2)
表示确认是否可以在机器上进行加工,为0~1决策变量的为:
(3)
表示同一个工件的不同工序之间加工时有紧前紧后关系的为:
Ci(j+1)≥Pij,∀i,j;
(4)
表示工件工序加工时间不得超过该工件所有工序完成的加工时间的为:
(5)
表示工件工序的加工时间不得超过最大完工时间的为:
Pj≤Cm
(6)
表示每个工件的不同工序可以循环在同一个机器上进行加工的为:
(7)
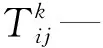
2 基于ALO单目标柔性作业车间调度
2.1 蚁狮优化算法
蚁狮优化(ALO)算法通过模拟自然界中一种生物—蚁狮狩猎蚂蚁的行为,对目标函数优化求解,借助于蚁狮周边蚂蚁的随机游走,以保证该算法的全局搜索能力。与粒子群等算法不同,该算法中有两个种群:蚁狮和蚂蚁,通过蚁狮对蚂蚁的捕获,实现种群的进化。ALO算法具有求解进度高、调参少等优点,得到了广泛的应用[8-12],但无人证明其求解柔性作业车间调度问题的有效性。
笔者尝试使用改进后的蚁狮算法求解柔性作业车间调度问题,证明其有效性。
2.2 蚁狮算法的数学模型
2.2.1 蚂蚁的随机游走及归一化处理
为保证蚂蚁随机游走在可行域的范围内完成搜索,笔者将进行归一化处理,使其运动范围在可行域内,如下式所示:
X(t)=[0,cumsum(2r(t1)-1),
cumsum(2r(t2)-1),…,cum(2r(tn)-1)]
(8)
(9)

(10)
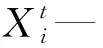
2.2.2 陷阱对蚂蚁随机游走的影响
笔者设计陷入陷阱边缘的蚂蚁运动过程受陷阱的影响,保证陷入陷阱的蚂蚁能够被蚁狮所捕获,如下式所示:
(11)

2.2.3 轮盘赌策略捕获方式
利用式(1)去计算适应度,根据蚁狮适应度大小利用轮盘赌策略来选择蚁狮,适应度越高的蚁狮有更高的捕捉蚂蚁的机会。
为提高算法的收敛速度,笔者将蚂蚁随机游走的范围随迭代次数的增加而缩小,其数学模型如下:
(12)
(13)
(14)
式中:t—当前迭代次数;w—随迭代次数而动态调整的参数;T—最大迭代次数。
2.2.4 捕获蚂蚁后重筑陷阱
当蚁狮捕获蚂蚁后,需重筑陷阱去捕获蚂蚁。若某只蚂蚁的适应度高于蚁狮的适应度时,则认为被蚁狮捕获,更新蚁狮位置,即:
(15)

2.2.5 精英更新
笔者利用轮盘赌选择的蚁狮和精英蚁狮的双重择优措施,对当前蚂蚁随机运动产生影响,将适应度最优的蚁狮作为当前最优的精英个体进行确定,并储存其信息,即:
(16)

2.3 蚁狮算法流程框图
不同于其他群智能算法,蚁狮算法在算法初始种群中引入了2个种群,即蚁狮种群和蚂蚁种群。笔者将能够抓住蚂蚁的蚁狮,即适应度最高、靠近最优解的蚁狮定义为精英蚁狮,运用轮盘赌策略选择一个适应度较好的蚁狮,让选择好的蚁狮和精英蚁狮同时进行捕猎,循环该过程,直到从中找到最好的解。
蚁狮算法流程框图如图1所示。

图1 蚁狮算法流程框图
2.4 编码解码
2.4.1 编码
由于传统的JSP问题只考虑工件工序的加工顺序,一般只是对工件工序进行设计编码,但是FJSP调度问题不仅要设计工序的加工方案,使其合理安排加工,不会出现因加工顺序安排出错,而导致加工冲突的事件发生,还要根据约束以及调度方案为每道工序设计合理的可加工机器,避免机器利用率不高,以及加工工序在机器上加工时出现冲突的情况发生,仅对工序的编码设计无法达到合理安排以及解决该问题。
因此,笔者使用基于工序和机器双层实数编码规则,该编码具体是针对工序以及加工机器两部分进行编码设计,达到合理解决加工工序间和机器间的冲突以及利用率不够问题的目的,且最终得到了正确可行的调度解。
为便于读者理解,笔者提出一个3×5的MOFJSP例子。现有工序集为O1={O11,O12,O13},O2={O21,O22},O3={O31,O32,O33};机器为M={M1,M2,M3,M4,M5}。
扩展的基于工序和机器的双层编码方式如图2所示。

图2 扩展的基于工序和机器双层编码方式
图2中:表示工件2的第1道工序可以在机器4上加工,工件1的第1道工序可以在机器3上加工,其表示的序列为:(O21,M4),(O11,M3),(O31,M1),(O12,M1),(O32,M2),(O13,M5),(O22,M2),(O33,M5)。
其中:基于工序编码的基因串是确定各个工件工序的加工顺序;基于机器编码的基因串为每个工件加工工序所对应的加工机器,机器的基因长度与工序的总数相等。
2.4.2 解码
解码是为了对设计的编码信息以及编码规则所形成的调度方案,利用甘特图的形式清晰地看出其是否合理安排了加工过程,根据甘特图所表示出来的问题进行进一步修改,直到找寻到最佳的调度方案,且不同解码设计方案也会产生不同的调度解,影响着最终调度结果的优越性。
因此,笔者利用插入式贪婪算法,根据编码信息以及编码规则进行解码操作。其具体过程为:找寻到加工机器的空闲时间,判断在该机器加工空闲时间里是否可以安排加工其他工件的工序。
基于插入式贪婪算法解码得到的甘特图如图3所示。

图3 基于插入式贪婪算法解码得到的甘特图
图3中:利用插入式贪婪算法对图2编码方式进行解码,得到可行解的甘特图,其中,图2编码方式的加工时间为[4,3,7,2,6,8,3,5];
机器5上共可以加工两道工序,即O13与O33,判断工序O13后是否有空闲时间,可将工序O33前插进行加工操作;机器2可加工两道工序O32与O22,判断O32之后有无大面积的空闲时间,将工序O32后插进行加工操作,这种操作可以使机器之间利用均衡,达到理想的加工效果。
2.5 混合策略的种群初始化
初始化种群的质量往往影响着最终求解结果。在蚁狮算法中,存在两个种群,即蚁狮种群和蚂蚁种群,且这两个种群都是随机生成的,这样随机生成的种群质量无法保证,进而影响算法的有效性。
在单目标柔性作业车间调度研究中,为解决蚁狮算法种群质量不佳的问题,笔者采用混沌映射策略以及锦标赛选择方式相结合的混合策略,生成初始种群改进蚁狮算法。
混沌映射是用于生成混沌序列,在确定的系统中生成随机序列,增强初始种群的混乱程度,即使初始始种群分布均匀。笔者使用混沌映射策略中的Logistic,即虫口映射方式,其递推方程如下:
zk+1=μzk(1-zk)
(17)
式中:zk—一数列。
其中:μ∈[0,4]。
笔者设定种群大小为100,其中,种群包括蚁狮种群和蚂蚁种群。利用混沌映射策略随机初始化生成蚁狮种群与蚂蚁种群,其大小分别为50,将随机生成的蚁狮种群和蚂蚁种群分别进行排序,取排序后的蚁狮种群中前1/5,即10个最优种群个体,作为下一代蚁狮种群。
为保证蚁狮种群不变,笔者在排序和选取后剩下的90个种群个体中,利用锦标赛选择方式,根据目标函数公式计算其适应度,挑选适应度最好的种群个体,以此来弥补下一代蚁狮种群中空缺的40个种群个体。这样可保证种群的多样性和种群质量,从而进一步减小了种群质量的好坏对算法的影响。
2.6 交叉变异操作引入
在单目标柔性作业车间调度过程中,为解决蚁狮算法收敛速度较慢、逃避局部最优能力弱以及对加工工序顺序的安排、加工机器的选择和利用率不高的问题,笔者将遗传算法的交叉变异操作引入蚁狮算法中。其具体过程如下:
2.6.1 交叉操作
在FJSP加工过程中,不仅需要确定工件i的所有工序j的加工顺序,还要对加工工序进行加工机器分配,针对该特点,笔者使用了两种交叉操作:
(1)单点交叉操作。用于对染色体中工序加工顺序的交叉,可更好地继承父代染色体中的优良基因;
(2)两点交叉操作。用于染色体中对工序加工机器的分配的交叉。
以下对两种交叉操作进行说明。
单点交叉又被称为简单交叉,它是指在父代染色体中的工序加工顺序基因段中随机选取一个随机点,交换两个父代在随机点前后的基因段,产生子代。
单点交叉如图4所示。

图4 单点交叉
图4中:在父代P1与P2工序加工顺序染色体中,随机选取一个随机点,交换父代P1与P2随机点前后的基因,产生子代C1和C2。
两点交叉操作是对父代染色体工序所分配的机器进行交叉,工序的加工顺序保留到子代。
基于机器编码的两点交叉操作如图5所示。

图5 基于机器编码的两点交叉操作
图5中:设父代P1和P2交叉产生子代C1和C2。两点交叉操作的过程为:随机在P1和P2中选择并设置两个交叉点,交换两个父代中所选定的两个交叉点之间的部分染色体,产生子代C1和C2,P1和P2中其他所分配的机器保留到子代。
2.6.2 变异操作
采用两种变异操作:(1)在工序编码染色体中使用插入变异操作方式;(2)利用单点变异操作进行工件加工工序机器的替换,从两方面进行变异操作。
笔者使用插入变异操作对工序进行变异操作,其工序的插入变异如图6所示。
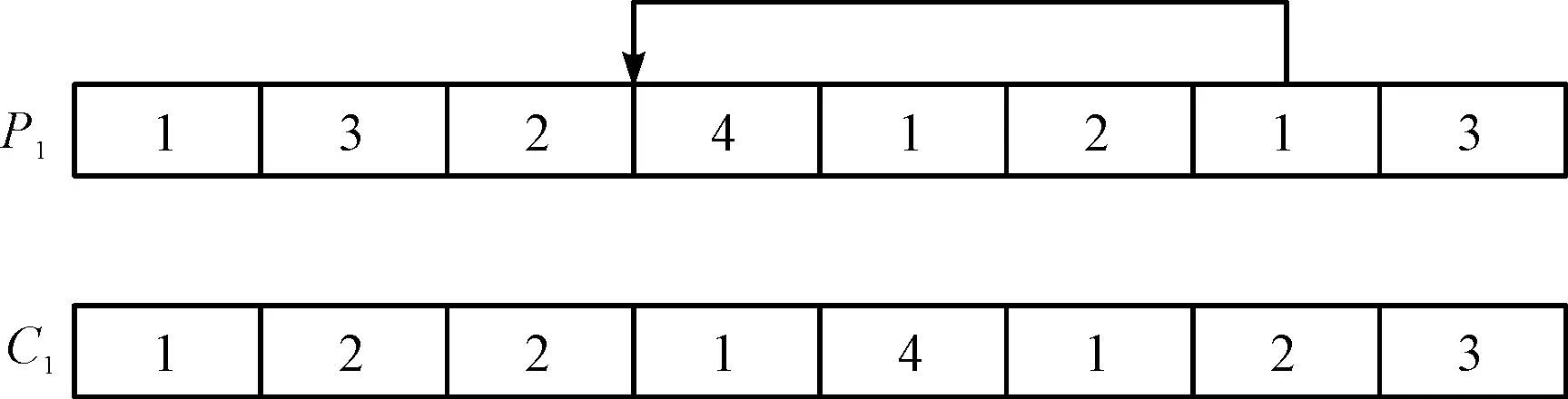
图6 插入变异
图6中:在工序编码的父代染色体中随机选择一个基因,将其随机插入某个基因前面或者后面,保持其他基因不变,产生子代。该变异操作对工序的安排进行一个随机化处理,让工序加工有更多的可能性,可更好地选择出一个合适的调度方案。
笔者采用单点变异操作进行工件加工工序机器的替换。基于机器编码的单点变异如图7所示。
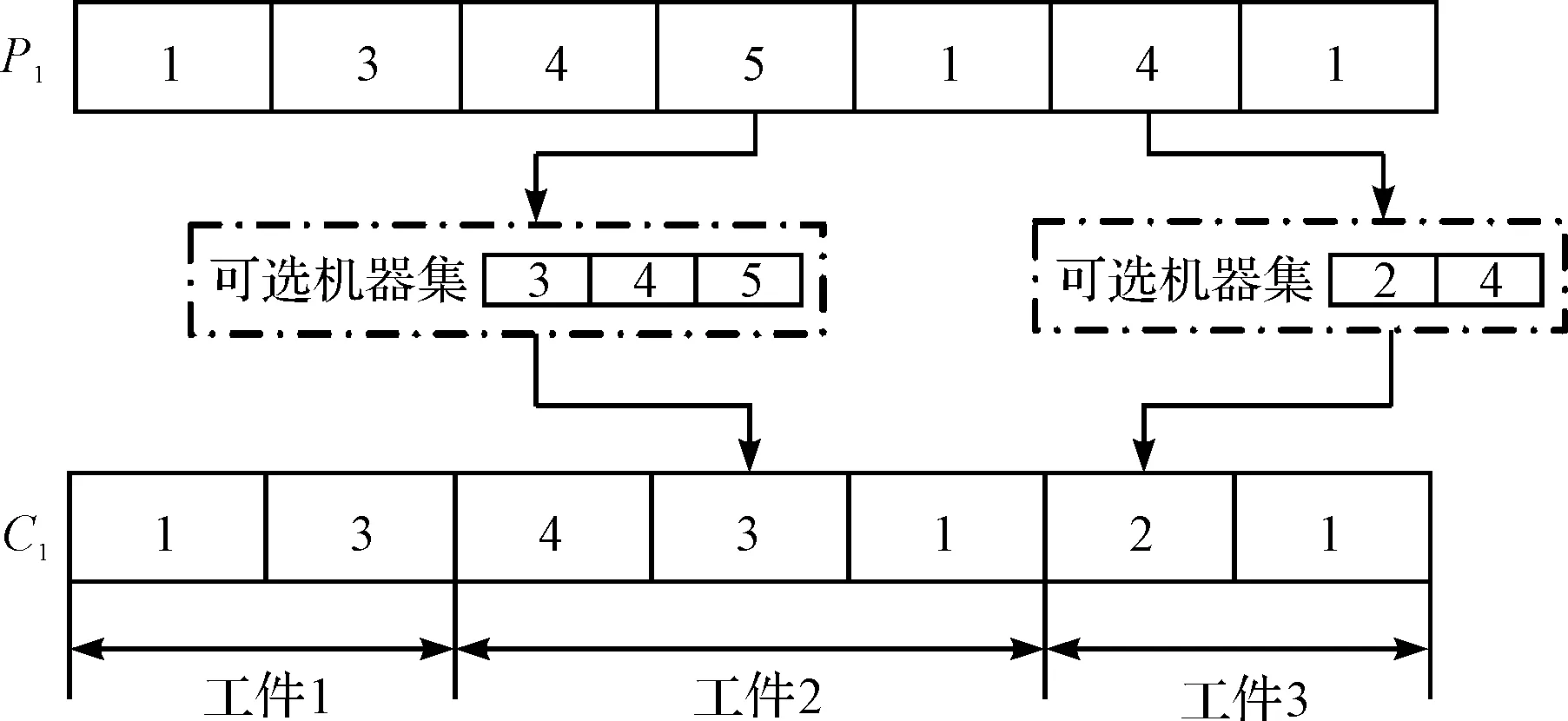
图7 基于机器编码的单点变异
图7中:笔者在机器编码的染色体中选择一个基因段,从该机器所加工的工序可选机器集中选择一个进行替换,可选择机器号小的机器来替换执行变异操作的基因段。
3 仿真实验分析
3.1 改进前后ALO算法的实验对比
为了验证改进的蚁狮算法在柔性作业车间调度上的有效性,笔者利用Brandimarte基准算例加工环境数据集(MK01—MK10)作为模型进行仿真测试。
MK01算例加工环境模型如图8所示。
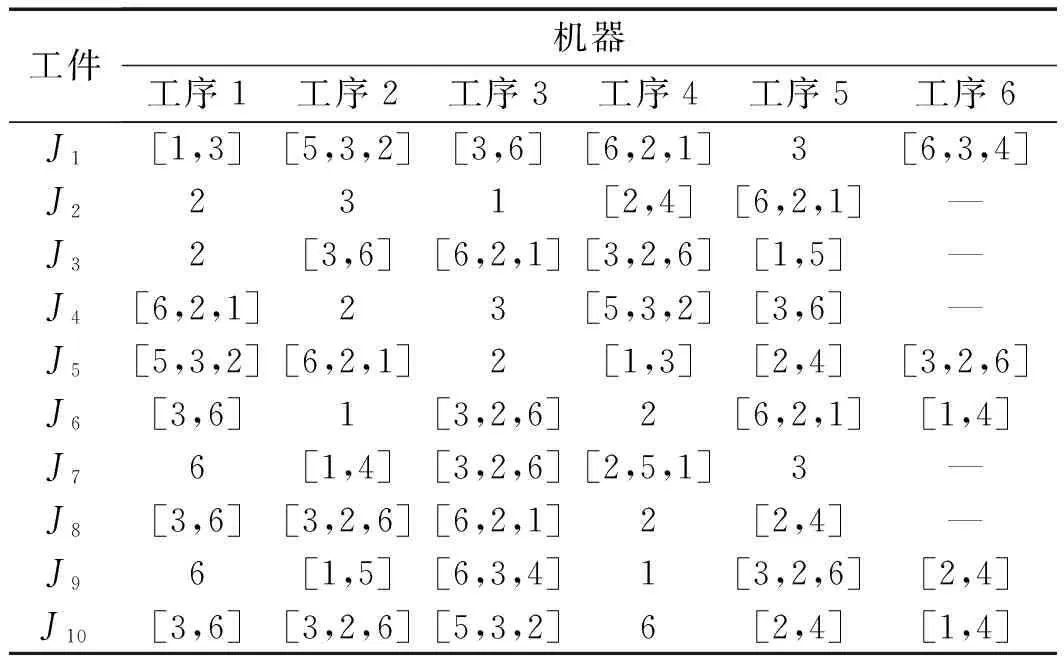
工件机器工序1工序2工序3工序4工序5工序6J1[1,3][5,3,2][3,6][6,2,1]3[6,3,4]J2231[2,4][6,2,1]—J32[3,6][6,2,1][3,2,6][1,5]—J4[6,2,1]23[5,3,2][3,6]—J5[5,3,2][6,2,1]2[1,3][2,4][3,2,6]J6[3,6]1[3,2,6]2[6,2,1][1,4]J76[1,4][3,2,6][2,5,1]3—J8[3,6][3,2,6][6,2,1]2[2,4]—J96[1,5][6,3,4]1[3,2,6][2,4]J10[3,6][3,2,6][5,3,2]6[2,4][1,4]
算法使用MATLAB2014b进行编程。运行环境为Windows10,Intel(R) Core(TM) i5-6200U CPU 2.40 GHz,内存4 GB,64位操作系统的个人笔记本电脑。
测试目标函数为1.2节中的式(1),算法参数设置为:种群大为100,迭代次数为200次,交叉范围(0.3,0.9),变异范围(0.1,0.25)。
笔者使用Brandimarte算例中的MK01基准算例,以最小化最大完工时间为优化目标,运行20次ALO算法;然后进行改进前后ALO算法对比,从迭代收敛图和甘特图可以明显地看出优缺点。
改进前后ALO算法迭代收敛对比图如图9所示。

图9 改进前后ALO算法迭代收敛对比图
图9中可以看出:第一次迭代时,改进前的时间是65,改进后的时间是49,验证了改进ALO算法利用混沌映射和竞标赛选择的混合初始化种群策略对初始化种群的质量有了极大的改善,保证了初始种群的多样性和质量;
ALO算法迭代160左右才找到最优解,而改进后的ALO算法迭代100次时就找到了最优解,且找到的最优解比改进前找到的解要小,说明改进ALO算法较ALO算法收敛速度快,能够快速地求解柔性作业车间问题;
其次,ALO算法在40代到135代之间陷入了局部最优,逃离局部最优的能力较弱,而改进的ALO算法仅在40代到100代之间陷入局部最优,逃离局部最优的能力有显著增强,加快了算法的收敛速度;
从加工时长来看,ALO算法最小最大完工时间最优为53,而改进ALO算法最小最大完工时间最优为40,明显提高了生产加工的速率。
为探究改进前后ALO算法优化FJSP问题的加工调度方案的优、缺点,可根据甘特图进行对比观察。
改进前后甘特图对比如图10所示。

在图10中可以看出:对机器5的利用率不高,只有两道工序在机器5上进行加工,且机器4的空闲时间较多,而引入了遗传算法的交叉变异操作,在机器5上加工工序变为了4道工序,明显提高了对加工机器的利用率,同时也使机器4的空闲时间减少,充分利用了固有资源,降低了生产成本,减少了完成加工的时间。综上所述,改进后的蚁狮算法更加适用于解决单目标柔性作业车间问题。
3.2 与其他智能算法的实验对比
为进一步验证改进蚁狮算法求解单目标柔性作业车间调度问题的有效性,笔者使用Brandimarte基准算例中的MK01-MK10基准算例,以最小化最大完工时间为单目标,运行20次算法,与姜天华等人[13]提出的混合灰狼优化算法(hybrid grey wolf optimization,HGWO)、PRASERT S等人[14]提出的改进微分进化算法(improved differential evolution,IDE)、CALDEIRA R H[15]提出的改进Jaya算法(improver Jaya algorithm, IJaya)、ALO算法,以及改进ALO算法的仿真结果进行对比。
Brandimarte算例对比结果如表1所示。
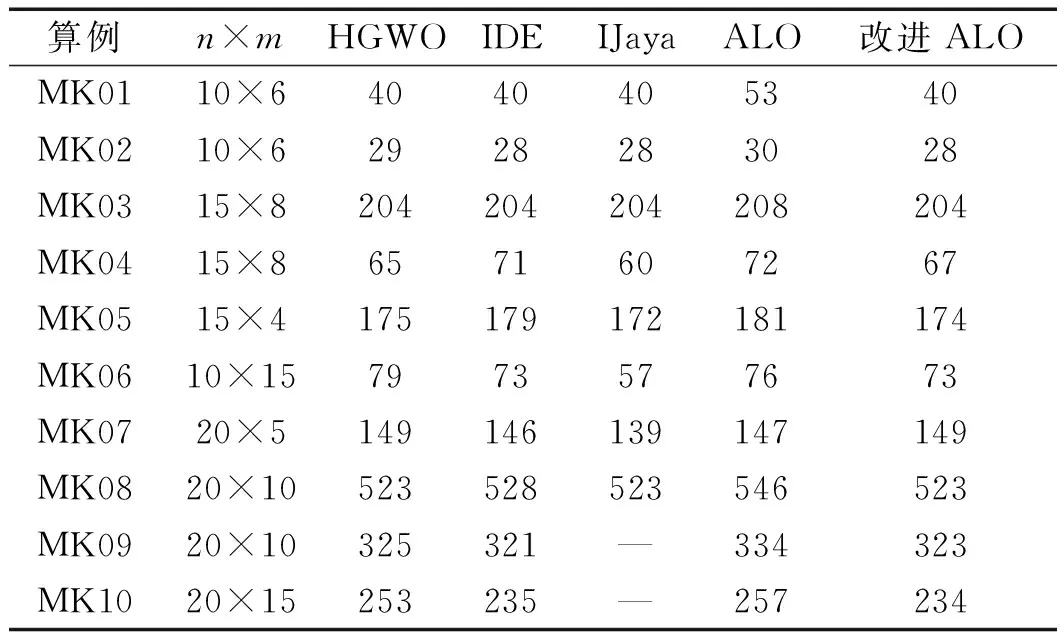
表1 Brandimarte算例对比
从表1中可以发现:改进ALO算法比ALO算法效果更加明显;与其他3种算法相比,改进后的ALO算法比HGWO除了MK03算例略差,MK01、MK03、MK07以及MK08这4个算例效果持平,剩下的5种算例均优于HGWO算法;
与IDE算法相比较可知,除了MK07和MK09以外,改进后的ALO算法均优于IED算法。与IJaya算法相比,改进ALO算法效果与其持平,没有体现出明显优于IJaya算法的趋势。
MK02算例下Makespe=28调度方案甘特图如图11所示。

图11 MK02算例下Makespe=28甘特图调度方案
综上所述,与改进前算法相比,改进蚁狮算法具有更强的收敛速度和不易陷入局部最优的特点;且在工序加工安排和加工机器的选择上,该算法可以极大程度地避免机器空闲和加工机器利用率不高的现象发生。
与目前单目标柔性作业车间调度问题的求解算法相比,该算法都具有优势。该结果表明,采用改进蚁狮算法求解单目标柔性作业车间调度问题是有效的。
4 结束语
笔者建立了以最小最大完工时间为优化目标的柔性作业车间调度模型,使用蚁狮算法求解柔性作业车间调度问题,通过实验证明,蚁狮算法可以求解柔性作业车间调度问题,但是也存在一定的缺陷,为此,笔者对算法进行了改进,提出了基于混沌映射与竞标赛选择的混合策略生成初始种群;引入了传统遗传算法中的交叉变异策略;通过Brandimarte基准算例的仿真结果与其他算法进行实验对比,验证了改进ALO算法求解柔性作业车间调度问题的有效性。
研究结论如下:
(1)蚁狮算法可以用于求解柔性作业车间调度问题,但会出现随机生成的初始种群质量不优、算法的收敛速度较慢、逃避局部最优能力较弱、最小最大完工时间较长、加工机器利用率低以及加工空闲时间较多等问题;
(2)蚁狮算法可以得到改进。首先,提出了基于混沌映射与竞标赛选择的混合策略生成初始种群,可以保证初始种群的质量和多样性;其次,引入了传统遗传算法中交叉变异策略,可以使该算法在迭代过程中,收敛速度加快,逃避局部最优的能力增强以及加工机器的利用率更高;
(3)通过利用Brandimarte基准算例,进行改进前后蚁狮算法实验对比,证明了改进ALO算法在解决该问题时,其收敛速度、逃避陷入局部最优的能力有明显的提升。
为进一步验证该算法的有效性,笔者将其与解决柔性作业车间调度问题的其他智能算法进行了实验对比,结果证明了该算法有较好的寻优能力和收敛速度,验证了该算法解决该问题的有效性。
在后续的研究中,笔者将根据现有的研究内容,将该算法运用到求解多目标柔性作业车间调度问题中,并对其进行改进,使该算法更加适用于求解实际柔性作业车间调度问题。

