基于改进阈值DT-CWT降噪与WPHM模型的滚动轴承可靠度评估*

赵红美,周志宏,杨胜兵

(1.唐山工业职业技术学院 机械工程学院,河北 唐山 063299;2.福州大学 机械工程及自动化学院，福建 福州 350108;3.福建省永安轴承有限公司,福建 三明 366000)

0 引 言

作为旋转机械最重要的支撑部件之一,滚动轴承广泛地应用于航空航天[1]、交通运输[2]、风力发电[3]等关乎国家基础设施建设和国计民生的重要领域,被誉为旋转机械系统的“心脏”。

但是在内外各种因素的综合作用下,使用过程中,滚动轴承的性能和健康状态会出现衰退的趋势,甚至在相同服役环境下,同种部件的可靠度也会出现几个数量级的差别。为了保证滚动轴承的健康运行,急需对轴承的运行可靠性进行评估,以实现滚动轴承的预测性维修,保证旋转机械设备安全稳定地运行[4]。

滚动轴承可靠性评估方法大致可分为以下3种,即基于模型的方法、基于专家系统的方法和基于数据驱动的方法[5],现详细分述如下:

(1)基于模型的方法。需建立准确的数学或物理模型来描述机械退化过程,并使用监测数据调整模型参数。基于模型的方法中,常用的有马尔可夫模型[6,7]、Winner模型[8]、高斯混合模型[9]等。但在实际应用中,针对复杂机械系统建立准确物理模型相当困难,使其在实际应用时受到了一定限制;

(2)基于专家系统的方法。不需要建立准确的物理模型,只须利用已有的信息,采用预测推理的方式对机械未来发展趋势进行估计。郭昆等人[10-12]将层次分析法、模糊综合评价法、模糊极小极大神经网络和动态模糊综合评判法等应用于滚动轴承可靠性评估和寿命预测中。但该方法受专家经验及知识库的限制,容易产生误判,且模糊系统、模糊规则选择的不确定因素众多,导致其得到的结论具有一定的不确定性;

(3)基于数据驱动的方法。在缺乏对故障预测先验知识的情况下,该方法的应用极为广泛。其应用主要集中在两方面,即构建可靠度指标和选择合适预测算法。WU Chun-zhi等人[13]提出了一种多尺度卷积神经网络,以频域特征作为模型的输入,构造了反双曲正切函数健康指标,以此来反映轴承运行过程中的退化状态。为解决传统方法在提取故障特征时造成的维数过高或者信息缺失问题,夏均忠等人[14]应用累积马氏距离实现特征降维,以此构建了轴承的健康指标。赵广谦等人[15]提出了一种基于卷积神经网络和双向长短时记忆网络的滚动轴承剩余寿命预测方法;该方法充分利用数据间的时序特性,实现了对滚动轴承剩余寿命的精准预测。

上述研究主要涉及滚动轴承的可靠性评估模型、专家预测推理知识、健康指标构建和预测算法选择等方面,并且以上研究也取得了卓越的成果。但是其在信号降噪、信号提取以及可靠性参数估计方面仍然存在不足之处。因此,急需要在海量信号的降噪、纯净信号的提取以及可靠性参数估计方法方面做进一步的优化研究。

笔者基于数据驱动的评估方法,利用改进的双树离散小波变换阈值降噪方法、粒子群优化算法和最小二乘法的融合算法,解决滚动轴承的提取数据失真问题,并快速寻找威布尔比例分布的最佳参数,从信号降噪和参数估计两方面探讨滚动轴承可靠性评估,提高滚动轴承预知性维修策略的准确性。

1 改进DT-CWT阈值降噪算法理论

1.1 DT-CWT理论

由于傅里叶变换存在缺乏局部化能力、对非平稳信号分析效果不好等缺点,笔者提出了一种具有多分辨率分析信号能力的小波变换[16]。通过不同尺度的“小波”来分解信号,能够很好地反映信号的局部特征[17]。

假设函数ψ(x)∈L2(R),L2(R)为平方可积复函数空间,其傅里叶变换为ψ′(x),则满足下式:

(1)

式中:ψ(x)—母小波;ω—采样频率。

将母小波进行伸缩和平移可得到一簇小波函数,如下式所示:

(2)

式中:a—尺度因子;b—平移因子;ψa,b(x)—小波基函数。

若有积分变换:

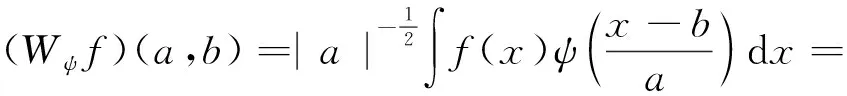
(3)

则称上述变换为f(x)以ψ(x)为小波基函数的连续小波变换。

由于连续性要求,导致连续小波变换在工程应用时的计算量巨大;并且,对尺度和平移参数采用极小的量化区间,会导致连续小波变换产生很大的冗余度。因此,笔者提出了离散小波变换(discrete wavelet transformation, DWT),将a、b离散化。

该处令a=2-j、b=2-jk,且j,k∈Z,则可得到:

(DWψf)(j,k)=[f(x),ψj,k(x)]

(4)

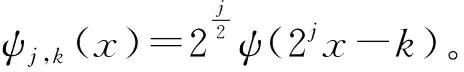
在工程实际中,使用小波变换时通常要对其进行离散化,然而其抽取过程却使DWT产生平移敏感性。虽然当信号产生很小的平移后,DWT在整体上能够实现信号的完全重构,但是其低通和高通分量也会产生变化。

小波平移分解性如图1所示。

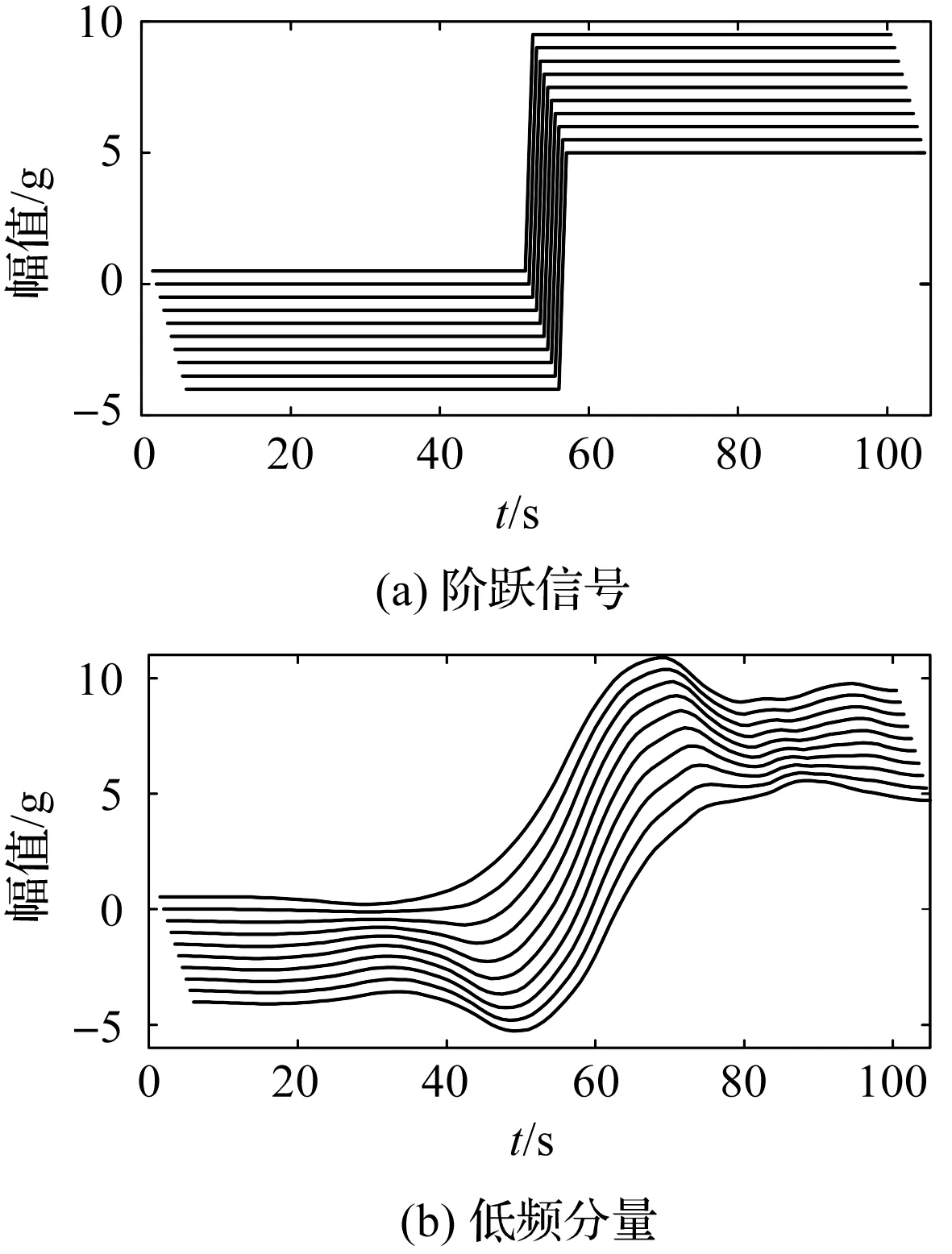
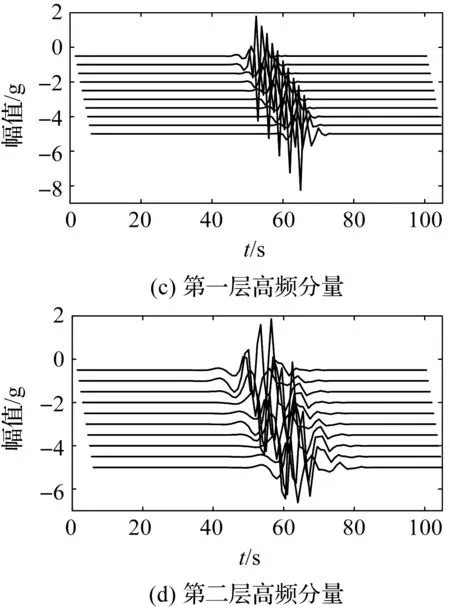
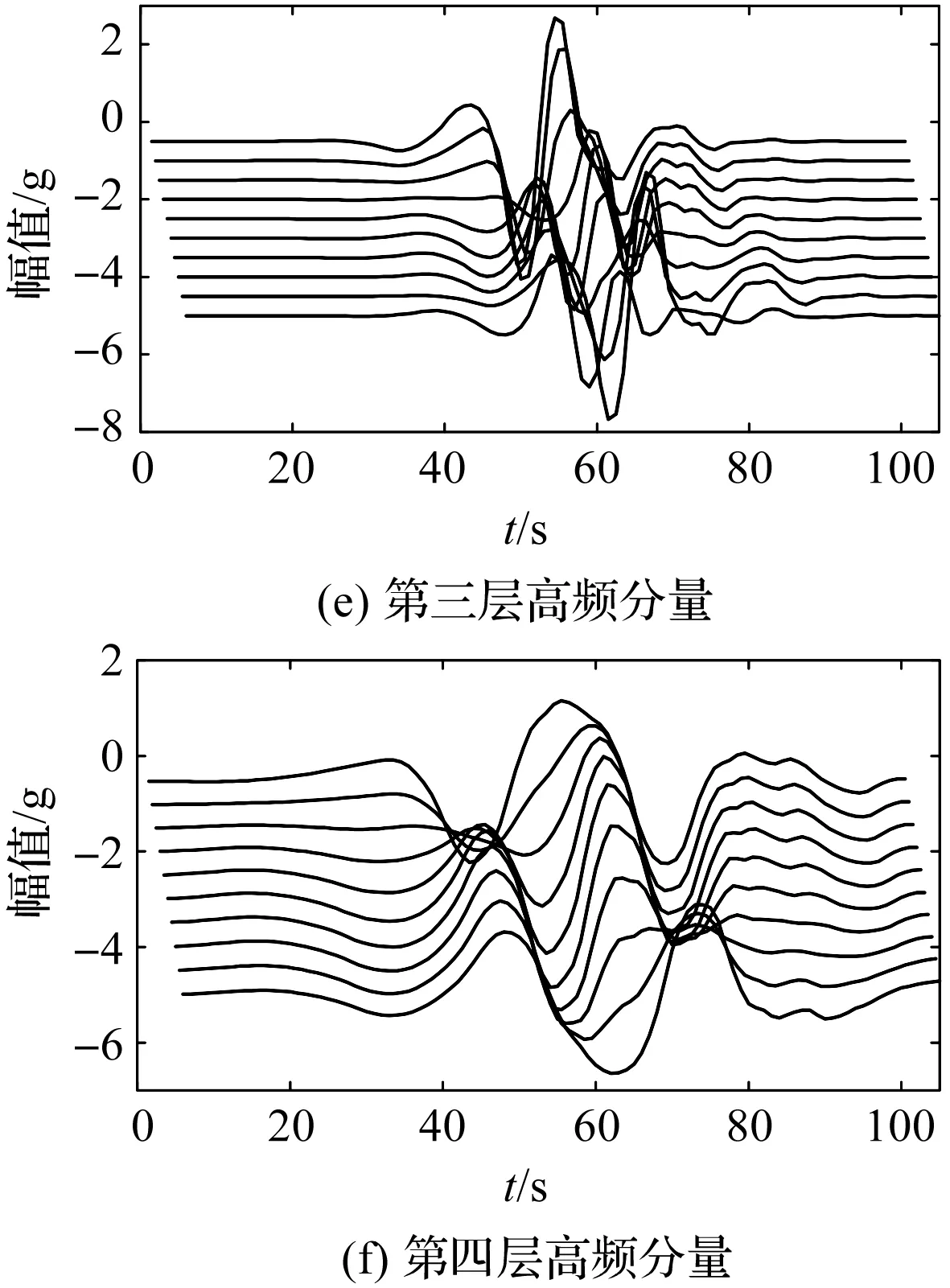
图1 小波平移分解性

阶跃信号在小量平移后进行4层离散小波分解,其低频和高频分量波形均产生变化,部分波形产生振荡,如图1(c～f)所示。在这种情况下,对低频和高频分量进行特征处理时,容易产生完全不同的特征信号;

此外,DWT在离散时间下的采样,容易导致信号在分解与重构过程中产生频率混叠[18]。常规DWT在处理不连续点或奇异点时,容易产生伪吉布斯现象,从而使重构后的信号在不连续点或奇异点两端产生震荡。

针对以上提到的DWT在信号分解与重构中产生的频率混叠现象,KINGSBURY N[19]提出了双树离散小波变换(dual-tree continuous wavelet transform, DT-CWT)方法,即通过两组平行且独立的低通和高通滤波器构成实部树和虚部树,实现对信号的完全重构。

采用DT-CWT实现对原信号完全重构的结构示意图,如图2所示。

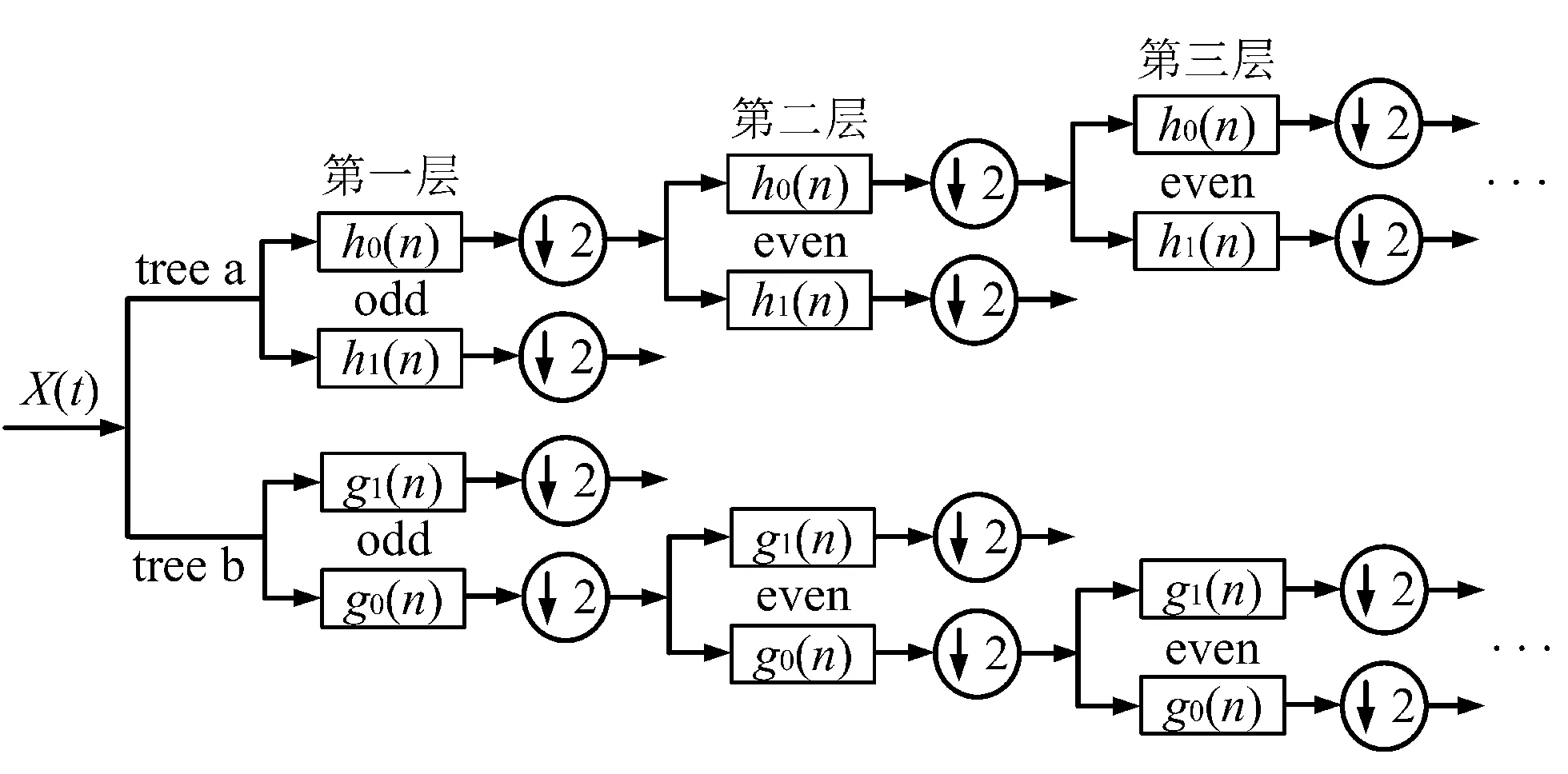
图2 DC-CWT结构示意图h0(n),h1(n)—tree a中的共轭正交滤波器组中的低通和高通滤波器;g0(n),g1(n)—tree b中的共轭正交滤波器组中的低通和高通滤波器;↓2—各点采样

图2中,tree a生成实部,tree b生成虚部。

笔者构造Q-shift滤波器组,第一层中tree a和tree b都采用奇数长度滤波器,分别对信号的奇数采样位置和偶数采样位置进行了滤波。第二层及更高层都使用偶数长度滤波器组,并且具有1/4采样周期的群延迟。这样保证了tree a和tree b相对于各自采样速率1/2个采样间隔的延迟,一棵树在下采样时始终能够取到另一棵树在下采样时舍去的采样值,从而实现其平移不变性[20]。

实部树tree a的小波系数和尺度系数为:

(5)

虚部树tree b的小波系数和尺度系数为:

(6)

则DT-CWT的小波系数和尺度系数为:

(7)

对信号进行重构后可得:

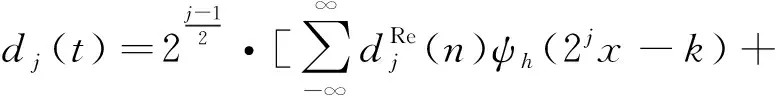
(8)

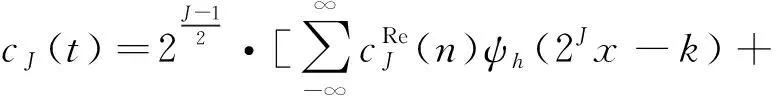
(9)

(10)

1.2 改进的阈值函数

传统的小波阈值函数分为硬阈值函数ω1(x)和软阈值函数ω2(x)。

两种阈值函数可以表示为:

(11)

式中:λ—阈值。

硬阈值函数是将小于阈值的小波系数全部置零,大于阈值部分原值保留。

传统阈值函数如图3所示。

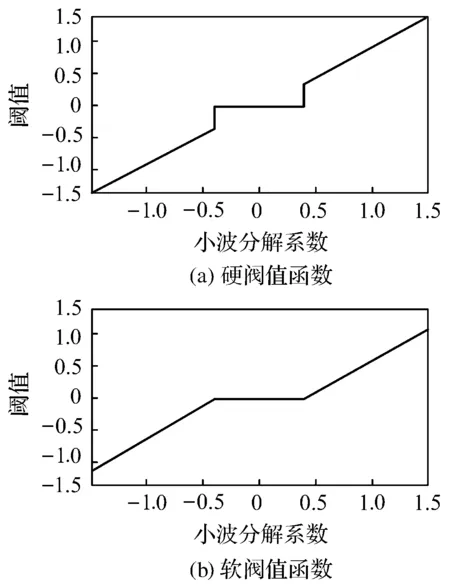
图3 传统阈值函数

由图3(a)可知：硬阈值处理导致小波系数在阈值点处存在间断点,使得降噪后的信号容易产生局部震荡,部分信号区域出现不连续现象或奇异点。

为了使降噪后的信号更加平滑,现在多采用软阈值函数,软阈值函数也是将小于阈值的小波系数全部归零,但是对大于阈值部分的小波系数全部进行了固定压缩,即把大于阈值部分的小波系数全部压缩到一个阈值。这样处理保证了降噪后信号的光滑性,如图3(b)所示。

虽然软阈值处理后保证了降噪后信号的光滑性,但是对大于阈值部分的小波系数进行压缩,造成部分高频信号损失,使得降噪后的信号与原信号存在部分失真。

基于目前硬软阈值函数存在的问题,笔者提出了一种改进阈值处理方法,既能解决硬阈值函数在阈值处尖端导致的不连续问题,又能减少软阈值压缩小波系数带来的信号失真问题。

改进的阈值函数如下:

(12)

改进的阈值函数如图4所示。

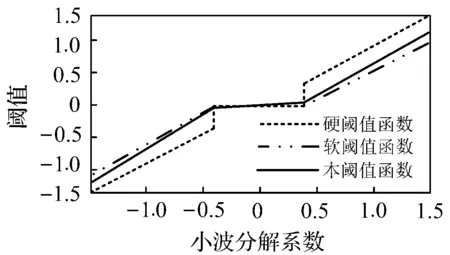
图4 改进阈值函数

由图4可知：改进的阈值函数在阈值点处连续,可改善硬阈值函数处理后信号的局部震荡问题。并且大于阈值部分的小波系数会随着小波系数的增大,而逐渐接近其自身真实值,可避免软阈值函数处理后,因小波系数与真实值之间存在固定值压缩而导致信号失真。

2 基于PSO与LS的WPHM参数估计

威布尔分布能够很好地描述“失效浴盆曲线”的3个失效阶段,其被看作一个个首尾相连的金属链环,整个复杂系统的整体寿命取决于最脆弱环节的服役寿命[21]。

由于威布尔分布在描述机械零件失效领域应用广泛,因此,笔者建立以威布尔分布为失效函数基底的比例风险模型,其失效函数λ(t)、可靠度R(t,zt)和累计分布函数1/(1-F(t,zt))如下:

(13)

式中:β—形状参数,β>0;η—尺度参数,η>0;γ—协变量回归参数;zt—协变量。

建立样本分布规律模型后,仍需根据样本提供的信息进行模型的参数估计,而参数估计的准确性能够决定分布模型最终效果的好坏。

笔者将粒子群优化算法(PSO)与最小二乘法(LS)融合,快速寻找到威布尔比例风险模型(WPHM)的最佳参数值。

最小二乘估计法需要将回归分析的样本点(xi,yi)列在二维直角坐标系中,利用一条直线进行回归拟合,即:

(14)

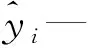
笔者根据微分极值定理、威布尔比例风险模型累积分布函数变换,以及取对数和偏导数求解等方法,得到如下结果:

(15)

笔者利用LS将非线性分布函数线性化后,并借助PSO,使目标函数的偏差平方和最小。

利用PSO的全局最优搜索策略与LS结合,能快速寻找到WPHM的最佳参数值。

PSO基本结构如图5所示。

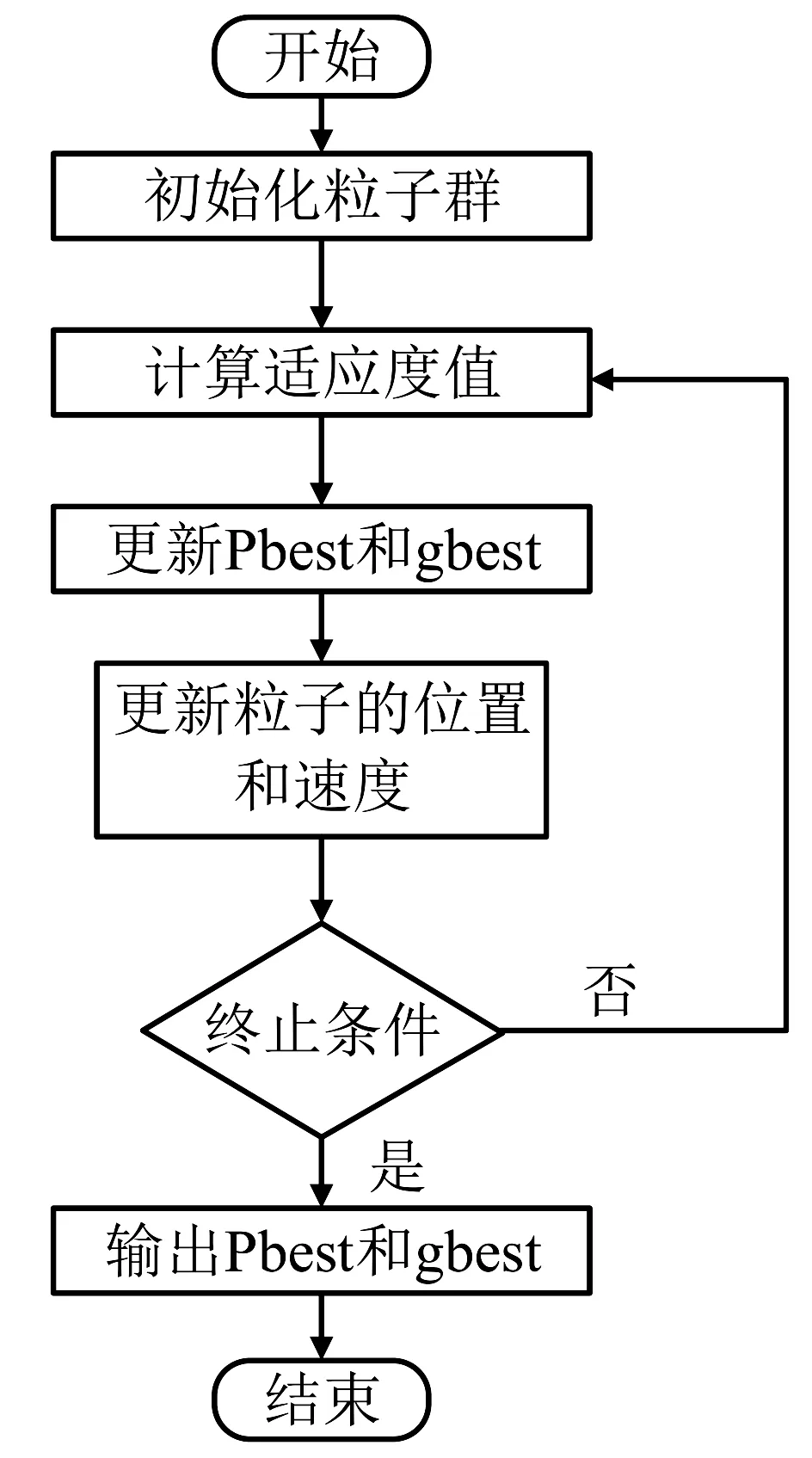
图5 PSO基本结构

PSO优化算法的基本步骤如下:

(1)设置种群参数,随机初始化种群;

(2)根据目标函数,确定适应度函数,并计算种群中所有粒子的适应度值;

(3)根据当前适应度值来寻找个体极值和群体极值;

(4)根据个体极值和群体极值对个体速度和位置进行更新;

(5)判断是否达到迭代终止条件,如果是则输出结果,否则需重复步骤(2)、(3)、(4)、(5)。

3 实验与结果分析

3.1 PRONOSTIA轴承实验台

正常轴承从健康状态到最终故障损坏,通常需要工作几千甚至数万个小时。到工厂中采集实时工况下的轴承全寿命数据比较难以实现,因此,笔者在此处选用了法国弗朗什孔泰大学FEMTO研究所的PRONOSTIA轴承实验台的数据[22]。

该实验台采用加速寿命实验方法,即对测试轴承进行加载或者增加转速,以达到加速失效的目的。

实验所使用的轴承均为同一型号滚动轴承,采样频率25.6 kHz,采样时长0.1 s,采样间隔10 s。当加速度幅值持续超过20 g时,认为轴承发生严重故障,则停止实验。

在实验中,20 g失效是实验设置的,与轴承的失效、塑性变形有一定关联。加速度传感器的型号是美国Dytran3035B,最大采集范围是50 g。

如果在测量过程中发现采集到的加速度信号幅值持续超过20 g,但轴承并未因为失效而停止工作,为了防止因轴承的破坏造成的实验台损坏,则可认为轴承已经发生了失效,实验结束。

在该实验中,轴承的加速寿命实验分3种工况进行,具体实验过程和实验台可参考文献[23]。

每种工况的转速及载荷信息如表1所示。

表1 工况信息

实验轴承的静态额定载荷为2 470 N,动态额定载荷为4 000 N,根据额定载荷及实际运转载荷计算轴承的额定寿命。

对于滚动球轴承,其额定寿命为:

(16)

式中:Cr—额定动载荷;Pr—当量动载荷;p—寿命计算系数,球轴承为3,滚子轴承为10/3。

将表1中的数据代入式(16),可得3种工况的寿命分别为9.259 3 h、8.725 6 h和5.688 9 h。

3.2 改进DT-CWT阈值降噪效果分析

该处笔者构造的轴承振动原始信号和仿真信号,如图6所示。

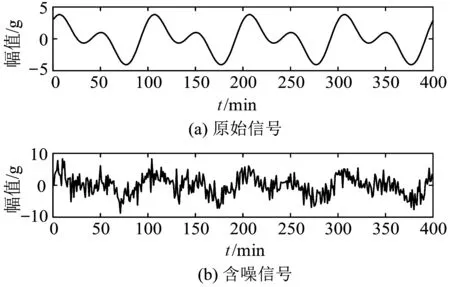
图6 仿真信号

软阈值函数、硬阈值函数和笔者提出的改进阈值函数降噪后的效果对比,如图7所示。

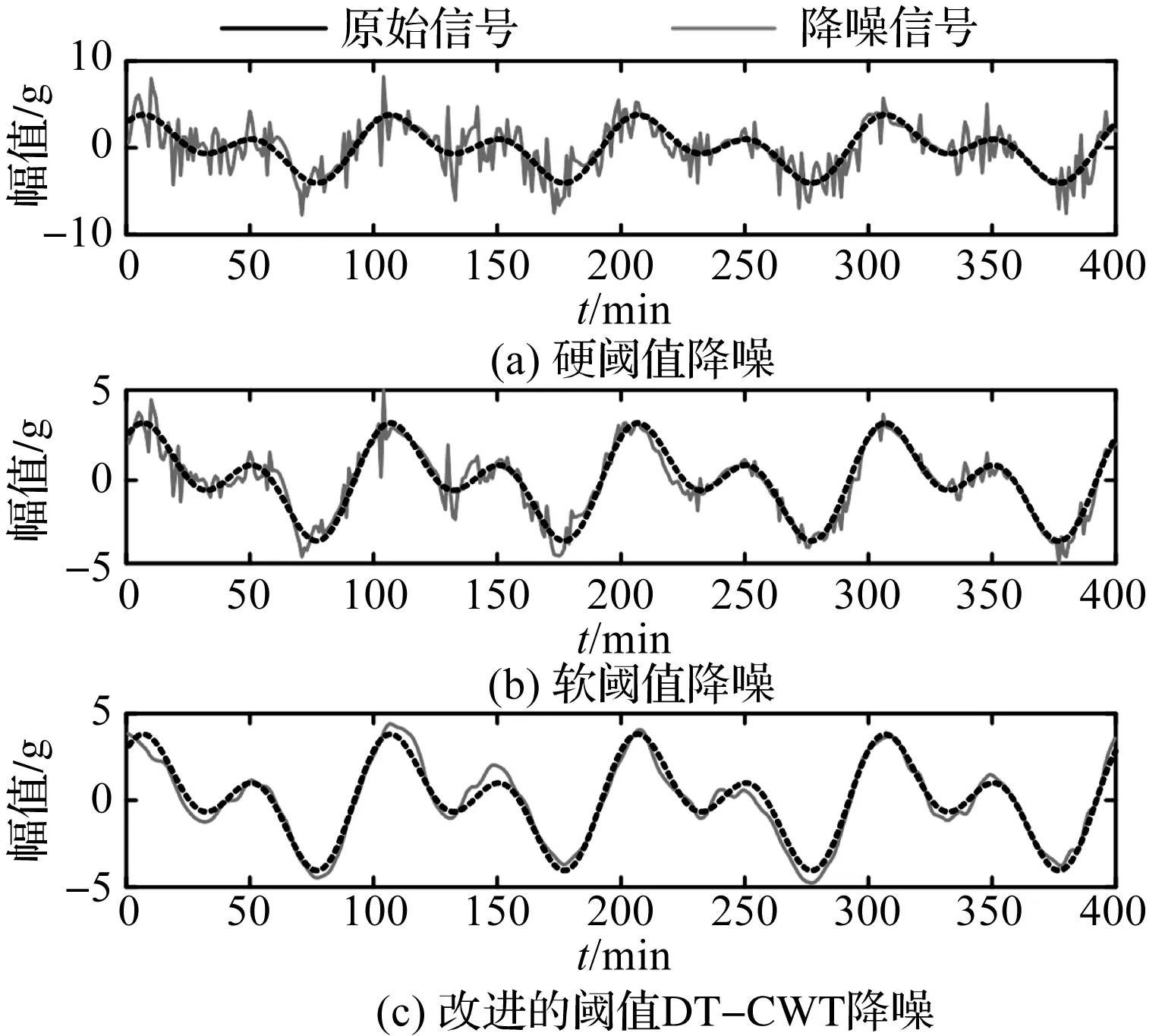
图7 阈值降噪效果对比

从图7中可以看出:通过构造高通和低通滤波器实现对信号的完全重构,传统软、硬阈值函数处理后的信号存在明显的局部震荡情况,毛刺突出部分比较明显,信号整体不平滑;使用改进阈值函数后,减少了降噪信号局部震荡的发生,并且降噪信号更接近原始信号。

综合比较可知,相对于传统阈值函数,改进阈值函数的降噪效果更好。

根据信噪比(signal-to-noise ratio, SNR)和均方根(root mean square error, RMSE)两种评价指标,笔者对软阈值降噪和改进阈值DT-CWT降噪方法进行对比。

降噪指标对比结果如表2所示。

表2 降噪指标对比

结合图7和表2可知:改进的DT-CWT阈值降噪可以提高信噪比,并且降低均方根差,降噪效果较好,可为后续轴承可靠度指标评估提供更加纯净的有效信号集。

3.3 WPHM可靠度指标评估

笔者采用PRONOSTIA轴承全寿命实验数据[24]进行了3层DT-CWT降噪,再针对分解出的小波系数,采用改进阈值函数进行降噪处理;将小波系数中的噪声部分清除后,重构得到降噪后的信号[25];对降噪的信号提取均方根等有量纲时域特征,以及峰值因子等无量纲时域特征。

有量纲时域特征结果如图8所示。

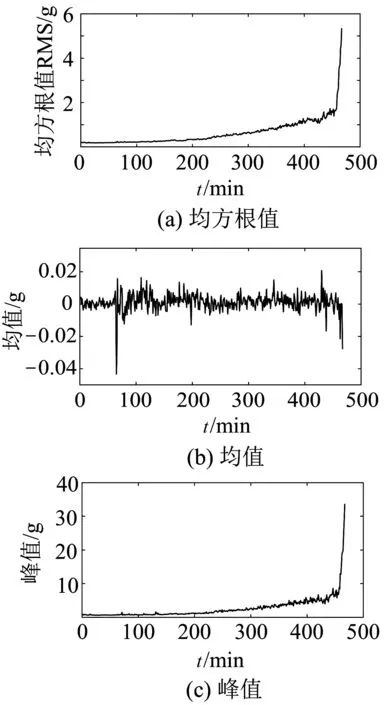
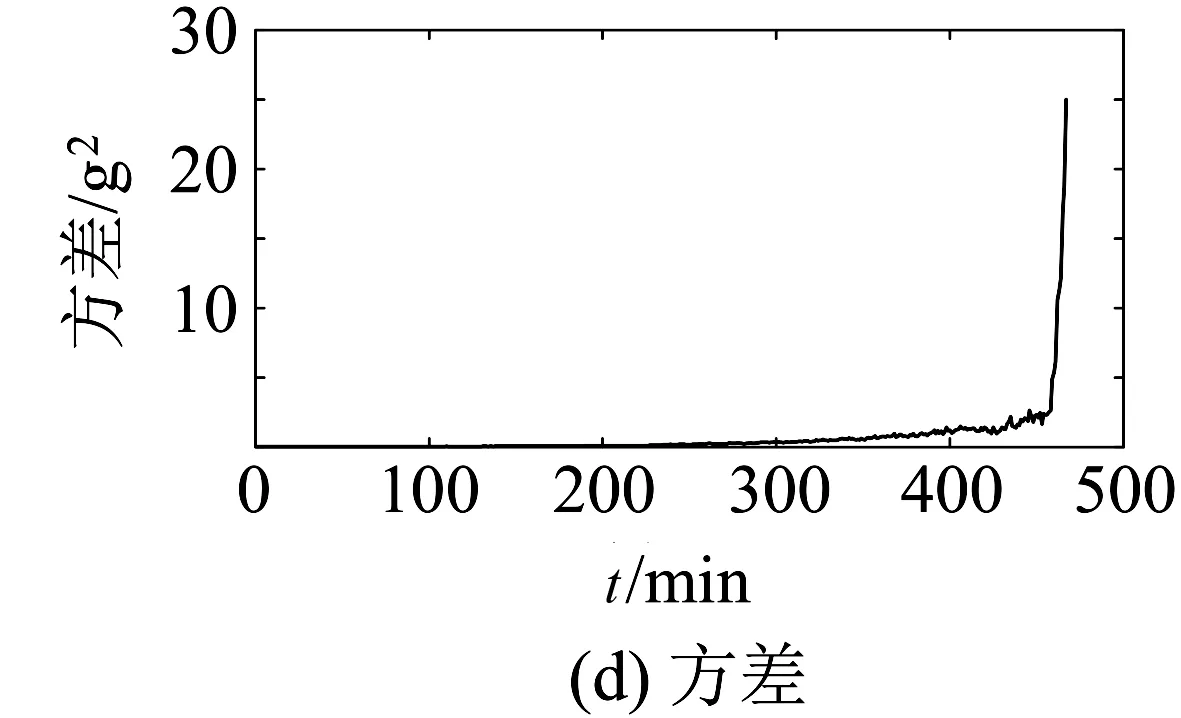
图8 有量纲时域特征

无量纲时域特征结果如图9所示。

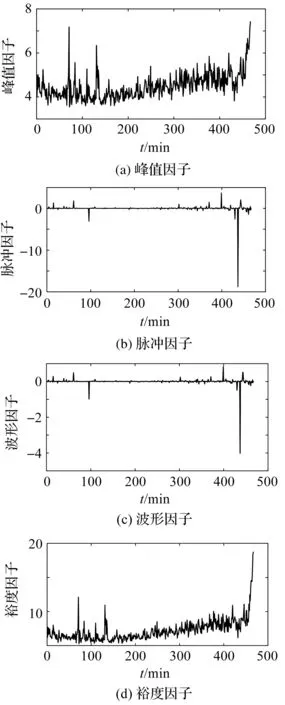
图9 无量纲时域特征

从图(8,9)中可以看出:在轴承可靠度较差时,有量纲时域特征中的均方根值、峰值和方差等指标较为明显,均会发生突变;而无量纲各个特征因子没有太明显变化。

为了更加准确地预估轴承的可靠度曲线,笔者利用PSO-LS方法进一步对WPHM进行参数评估。

β、η和γ这3个参数的估计结果如表3所示。

表3 参数估计

笔者将参数估计结果代入式(13)中,通过将WPHM中的目标函数进行线性变换,并使用LS进行参数估计,建立合适的WPHM模型,以此来计算轴承的可靠度曲线。

轴承的可靠度曲线如图10所示。

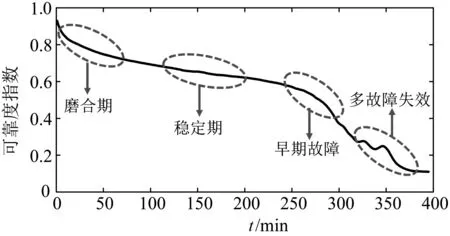
图10 轴承的可靠度曲线

由图10可知：当可靠度指数为1时,表示轴承处于完全健康状态;而当指数为0时,表示轴承处于报废下机状态。

根据轴承的可靠度曲线变化还可以看出:轴承的可靠度总体呈下降趋势,与轴承在使用过程中的退化趋势相符。早期轴承可靠度下降较快,轴承处在磨合期,此时振动幅值变化较大;当磨合期过后,轴承可靠度下降相对较缓慢,此时轴承运行状态和性能都处于一个稳定状态;随着运行时间增加,轴承开始出现早期故障,并且故障不断积累扩展,运行工况逐渐恶劣。此时轴承状态波动较大,可靠度有明显下降的趋势,并且随着多故障综合影响,可靠度也出现一定波动。故障逐渐积累,振动信号幅值已经出现大幅增加,可靠度降至低点,最终轴承故障失效。

通过对比3种实验工况的失效寿命时间可知:通过WPHM模型计算得到的可靠度评估曲线介于工况2和工况3之间,符合轴承使用过程中的实际情况。因此,能够将WPHM模型作为轴承在不同阶段的健康指标,以反映轴承的健康状态。

4 结束语

滚动轴承作为旋转机械的核心部件,其运行状态关乎整个机械系统的安全与稳定。针对滚动轴承海量运行数据降噪困难和可靠性预测精度不高等难题,笔者提出了改进的DT-CWT阈值降噪函数,基于PSO-LS对WHPM模型进行了参数估计,并进行了仿真分析和实验验证。

研究结果如下:

(1)改进的DT-CWT阈值降噪函数解决了传统软、硬阈值函数处理后信号存在的局部震荡、毛刺突出和信号整体不平滑等问题,并且其降噪信号更接近原始信号。相对于传统阈值函数,改进阈值函数的降噪效果更好;

(2)在SNR和RMSE两种评价指标对比下,利用改进的阈值降噪函数可提高SNR 58.2%,降低RMSE 58.3%;

(3)PSO-LS算法解决了WPHM模型中的参数估计问题,并且加快了算法的计算速度,得到的可靠度评估曲线符合轴承使用过程中的实际情况,能够将其作为轴承在不同阶段的健康指标,以反映轴承的健康状态。

随着机械装备的不断更新,滚动轴承经常处于复杂变工况的服役环境下,积累了大量带故障的数据样本,并且轴承故障的样本也呈现微弱、混乱的特征。因此,如何更精确地清洗样本,并增强故障特征是实现寿命预测的关键环节,这将是笔者今后的研究方向。