考虑多普勒效应的列车轴承参数驱动声学故障诊断模型*

滕繁荣,刘 方*,翟中平,侯超强,翟涛涛,刘永斌

(1.安徽大学 电气工程与自动化学院,安徽 合肥 230601;2.中国科学技术大学 精密机械与精密仪器系,安徽 合肥 230027)

0 引 言

轮对轴承是列车的关键部件之一,如其发生故障,将可能导致列车脱轨事故的发生。

现有的列车轴承在线健康监测技术主要分为两类:(1)车载监测;(2)轨边监测。前者将传感器安装在列车上,后者将传感器安装在铁路两侧。比较这两种技术后可以发现,后者采用的是非接触式测量,其具有低成本的优势。

目前,常见的轨边监测系统有两种检测方法:(1)热轴承检测系统(hot bearing inspection system,HBD);(2)轨边声学检测系统(trackside acoustic detection system,TADS)。在TADS系统中,铁路两侧安装麦克风,当列车经过时,轴承发出的声音信号被轨道边的麦克风采集,对信号进行处理,即可实现对轴承健康状况的判别。与热轴承检测系统(HBD)相比,轨边声学检测系统(TADS)具有早期故障检测的能力和优势[1-3]。

然而,由于列车在高速运动过程中,多普勒效应会对轴承声音的信号产生影响,导致其时域的幅度调制和频域的非线性偏移,这会对列车轴承振动信号的有效分析和对轴承故障的精确诊断带来困难。

目前,信号校正是解决上述问题的主要方法。在信号校正法中,最常用的是时域插值重采样(time domain interpolation resampling,TIR)方法[4]。在时域插值重采样方法中,多普勒频移信号被一个新的时间序列(根据声源和麦克风之间的距离变化计算出来)重新采样。然而,在采用该方法时,其运动学模型的参数应该是已知的,或预先测得的。引入参数估计算法可以解决该问题,例如希尔伯特变换(Hilbert transform,HT)[5]和短时傅里叶变换(short time Fourier transform,STFT)[6]两种瞬时频率估计(instantaneous frequency estimation,IFE)方法。在这些方法中,可以通过信号的IFE获得重采样时间序列。因此,它是一种基于信号的,无需外部传感器的校正方法。

然而,当背景噪声较强时,采用上述方法提取瞬时频率会变得困难。

基于匹配追踪的方法,可以通过Doppler-let变换来实现估计参数[7],但其匹配追踪算法计算量较大。在此基础上,ZHANG Shang-bin等人[8]引入了均匀线性阵列(uniform linear array,ULA)和时变空间滤波重排(time-varying spatial filter rearrangement,TSFR)策略;与单个麦克风的方法相比,该方法采用了更多麦克风同时捕获轨边信号,并且可以设计基于多径信号时间延迟机制的TSFR,通过瞬时能量图(instantaneous energy map,IEM)来自适应消除多普勒效应。

在该方法中,信号校正的精度取决于空间滤波的方向性精度。但是,估计的声源位置存在误差,当声源距离麦克风较远时会出现跳变现象。

后来,LIU Xing-chen等人[9]提出了一种结合ULA的匹配追踪算法。多普勒畸变的自适应校正可以通过参数化原子匹配识别参数来实现。但由于原子参数较多,其计算成本相对较高。

近年来,卷积神经网络(convolutional neural network,CNN)在故障诊断领域得到了广泛的应用,是目前使用最为广泛的神经网络之一,具有良好函数逼近能力[10-12]。

笔者尝试将多普勒效应对信号的影响看作传递函数DTF,使用CNN建立直接DTF-1来解决多普勒畸变问题。具体来说,即笔者设计一种运动学参数驱动卷积神经网络(kinematic parameters drive convolutional neural networks,KPD-CNN),以此来构建DTF-1。但是CNN的准确构建需要足够多的代表性样本(故障类型),这在工程应用初期很难满足,因为在应用初期,系统采集到的样本大部分是健康样本。因此,样品不平衡问题将严重影响模型的准确建立。

安全域分析是近年来系统状态评估中常用的一种方法。该方法属于一种二分类模型,仅使用安全样本构建一个名为安全域模型(security realm model,SRM)的分类模型[13-15],以有效识别系统状态是否安全。该方法最早应用于电力系统的安全状态评估[16],后来被推广到网络控制、公路交通和电子政务等领域[17,18]。

近年来,安全域的基本概念被引入轴承故障诊断和铁路运输等领域[19]。最近,SRM内核参数的新优化方法被提出,同时成功地采用了一种源自SRM的指标,用于对高速列车轴承的健康进行评估[20]。在TADS系统应用的早期,系统采集的样本大部分是健康样本。因此,SRM非常适合现阶段的应用。

笔者针对TADS声信号的畸变特点,基于SRM方法,提出一种运动学参数驱动安全域模型(kinematic parameters drive security realm model,KPD-SRM),用于在应用初期样本不平衡时诊断模型的建立。通过这种方法可以不断积累数据样本;当积累了足够多的具有代表性的数据样本时,就可以使用KPD-CNN模型建立准确的故障诊断模型。

综上所述,笔者提出一种KPD-SRM/KPD-CNN的列车轴承智能诊断方法(包含两个改进的学习模型,其中,KPD-SRM用于应用初期阶段的样本积累,KPD-CNN用于后期代表性故障样本积累足够后的诊断模型的建立)。

1 参数驱动学习模型

1.1 TADS模型

轨边声学检测系统(TADS)模型如图1所示。

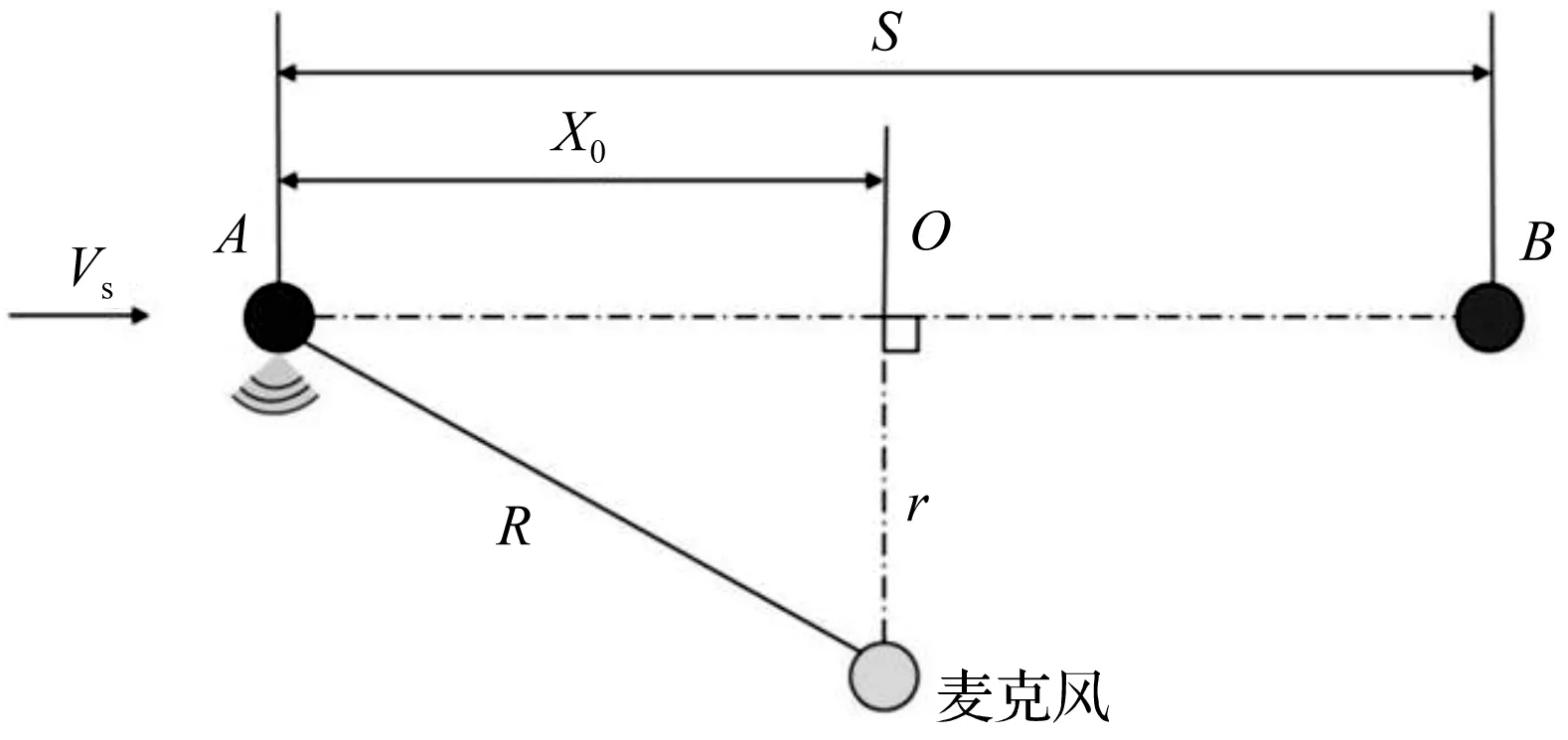
图1 TADS的基本示意图

由于轴承声源相对麦克风运动,麦克风采集到的声源信号会有多普勒效应影响,导致在时域和频域中失真,这将严重影响故障诊断的准确性和有效性。

多普勒效应对信号时域和频域的影响可以分别表示为:

(1)

(2)

式中:X0—信号初始时刻麦克风与声源的距离;r—声源运动过程中麦克风的最近距离;f0—故障频率;VS—声源运动速度;M=VS/c;c—声音的传播速度。

多普勒效应对信号在时域和频域的影响是由{r,X0,VS,c,f0}这5个变量决定的。在这些变量中,f0是由信号本身的特性决定的;而声速c是1个与环境有关的物理量,在实际应用中可以看作是1个常数值。所以多普勒效应对信号的影响可以用以下3个参数来描述:γ={r,X0,VS}。

因此,可以通过公式来描述多普勒效应对信号的影响:

DTF=f(r,X0,Vs)

(3)

通过进一步分析可以发现,对于同一类型的列车,r是一个固定值。而在实际应用中,X0也可以设置为固定值。例如,可以在图1中的A点和B点设置距离检测传感器,利用位置检测传感器脉冲信号截取轴承信号。因此,对于同一类型的列车,多普勒效应的影响主要由VS决定。

笔者使用仿真分析来研究多普勒效应对信号的影响。根据图1所示模型进行仿真,仿真参数设置如下:X0=10 m,r=1 m,c=340 m/s。声源移动速度VS为15 m/s和100 m/s之间,以5 m/s的间隔设置总共18个值。轴承信号的多普勒调制是通过多普勒发生器来实现的。在仿真中,选择美国凯斯西储大学提供的轴承信号作为声源信号[21]。

轴承信号在麦克风相对轴承静止的状态下采集,数据信号包含健康状况(Healthy)以及3种故障:外圈故障(outer ring failure,ORF)、内圈故障(inner ring failure,IRF)和滚子故障(roller failure,RF),3种故障对应故障尺寸为0.177 8 mm、0.355 6 mm和0.533 4 mm,共10种轴承信号样本,如表1所示。

表1 轴承信号

经短时傅里叶变换得到的部分模拟信号的时频分布,如图2所示。

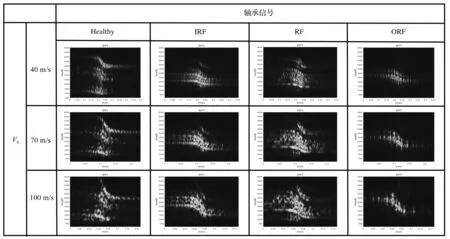
图2 多普勒频移轴承信号的时频分布图

从图2中可以看出:多普勒效应给信号时、频域带来了失真,并且随着速度的增加,失真程度增加。

在故障诊断领域中,通常利用信号的特征来表示故障的相关信息。

该方法中共有8个统计特征,分别是波形因数(waveform factor,WF)、方差(μ)、余量因数(margin factor,MF)、峰度(kurtosis,K)、频率集中度(frequency concentration,FC)、脉冲因数(impulse factor,IF)、波峰因数(crest factor,CF)、频率标准偏差(frequency standard deviation,FSD),如表2所示。

表2 8种统计特征

为了消除多普勒效应对轴承信号的影响,可以利用DTF的反函数DTF-1来进行消除,这样就可以直接根据采集到的原始信号进行故障诊断,不需要事先对信号进行校正。

笔者所提出方法的详细过程如图3所示。

图3 笔者所提方法的详细过程XD—轨道旁的麦克风收集的具有多普勒效应的声音信号;γ—描述系统运动学模型的参数集

在现有方法中,为了解决XD的多普勒效应,需要先对XD进行信号校正。而笔者所提方法不需要进行多普勒失真校正,而是直接从采集的信号XD中提取特征FD,利用DTF-1进一步消除了多普勒效应影响,从而得到静态采集的声源信号中的特征向量F;然后,通过传统的诊断模型进行故障决策。

但是,DTF-1很难在数学上建立表达式,因为这涉及到声学理论。在实际工程应用中,轴承声源信号也很难准确地用数学表达式表示。

鉴于卷积神经网络在变量间函数关系未知的前提下,可以通过数据样本的学习,建立两个变量间的函数关系。因此,在该研究中,笔者尝试使用卷积神经网络建立DTF-1。

1.2 基于参数驱动的学习模型

传统的CNN是构建特征与故障诊断决策之间的关系,而笔者采用运动学模型与传统的特征共同构建信号特征与故障诊断决策之间的关系,因此,将其命名为运动学参数驱动CNN,如图4所示。

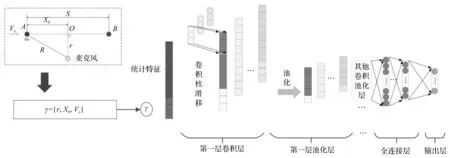
图4 运动学参数驱动CNN

KPD-CNN作为一种有监督的机器学习方法,需要大量具有不同轴承故障类型和不同故障级别的数据集。但在工程应用初期,采集的样本大多为健康样本,很难获得足够有代表性的数据样本,数据集不平衡的问题会影响KPD-CNN的准确建立。

为了解决数据集不平衡问题,笔者提出了一种基于支持向量数据描述(support vector data description,SVDD)的KPD-SRM方法。SRM是一个二分类模型,健康样本的特征向量构建一个最小安全区域,当测试样本的特征向量在该空间内时,认为该样本是健康样本,反之则认为是故障样本。

笔者利用决策函数来判断样本是否属于安全区,即:

f(x)=sign[Bound(x)],x=(F,γ)

(4)

式中:F=(F1,F2,…,Fn)—样本的特征向量;n—特征个数;Bound(x)—边界函数。

笔者添加运动学参数γ={r,X0,VS},构造新的特征向量D={x1,x2,…,xn+3}。其中：D—TADS系统工程应用早期采集的健康样本的特征向量和运动学参数。

笔者采用SVDD获取半径最小的超球面,并尽可能地包含所有的健康样本。

超球面应满足下式:

(5)

式中:Φ(xi)—样本的核空间映射;ξi—松弛变量;C—用于平衡T和ξi的惩罚参数。

通过拉格朗日乘子,可以得到拉格朗日函数:

(6)

根据Wolfe对偶定理,可以等价于下式:

(7)

其中:κ(xi,xj)=(Φ(xi),Φ(xj))。

一般采用径向基函数作为核函数。通过求解上式,可以得到a的最优解为∑αi*Φ(xj)。

半径T是球心a到支持向量xk的距离,即:

T2=‖Φ(xp)-a‖2=

(8)

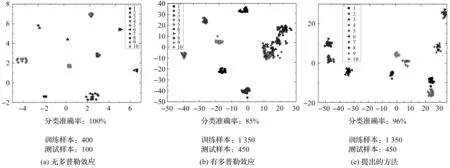
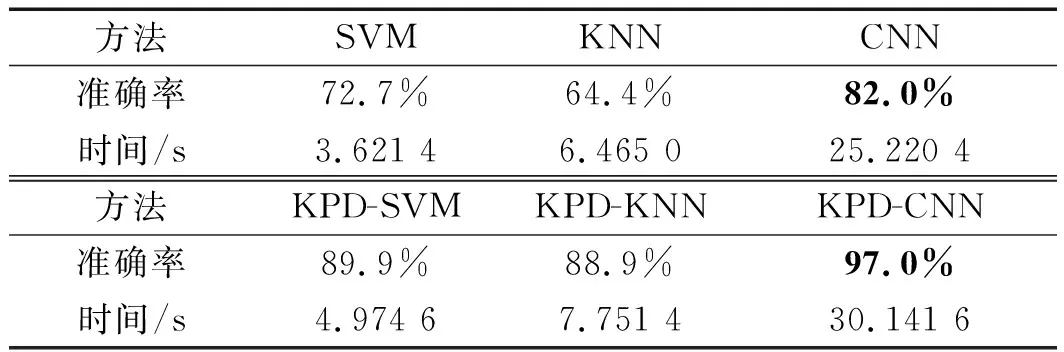
式中:xp—对应于0<αi

如果测试样本到a的距离小于T,则认为是安全的;否则,则认为是不安全的。

结合上述2种学习模型,笔者提出了KPD-SRM/KPD-CNN方法,如图5所示。

图5 基于参数驱动的学习模型

图5中,第一个模型用于初始阶段故障诊断,并积累样本;当积累了足够多的多类代表性数据样本时,用第二个模型进行故障诊断。

与现有方法不同,该方法不需要预先进行信号校正。该方法具有以下优点:

(1)与现有的信号校正方法相比,除了声源速度外,无需进行参数测量;(2)采用机器学习方法,可以利用历史数据提高诊断准确率,并随着监测样本的增加而不断提高;(3)提出的参数驱动模型可以有效解决初始应用中的样本不平衡问题。

2 仿真验证

2.1 KPD-SRM有效性

为了验证上述基于参数驱动的学习模型的有效性,笔者对仿真数据进行分析。

为了测试KPD-SRM模型/方法的有效性,笔者进行3个案例的分析:

(1)使用传统SRM分析无多普勒效应的轴承信号;(2)使用传统SRM分析有多普勒效应的轴承信号;(3)使用KPD-SRM分析具有多普勒效应的轴承信号。

其中:案例(1)的数据集包含10种类型轴承信号,每种类型有50个样本,命名为数据集A;案例(2)的数据集包含10种类型轴承信号,每种类别180个样本(18种不同速度下的轴承信号),命名为数据集B。

笔者使用数据集A的40个健康样本作为训练数据集,构建安全区域,其余10个健康样本和450个失效样本作为测试数据集;通过网络搜索算法,得到训练后的SRM的最优惩罚参数C为0.29。SRM测试集的准确率为99.1%。

由于SRM是高维的,无法直接可视化,因此,笔者选择了8个特征中的2个来重新训练模型。

SRM的降维可视化如图6所示。

图6 SRM的降维可视化

其中,图6(a)显示了使用F2和F8作为输入向量构建的SRM;图中,圆圈代表训练样本分布,正方形代表支持向量点。在案例(2)、案例(3)中,训练集与测试集与案例(1)中保持同样的比例;

图6(b)显示了受多普勒效应影响后识别率下降到90.3%,说明多普勒效应降低了特征的可分离性。

由于案例(3)中使用的KPD-SRM同时使用声源速度和统计特征作为输入,使识别率提高到97.5%。

由此可见,笔者所提KPD-SRM方法是有效的。

上述仿真分析验证了笔者所提出的KPD-SRM的有效性,KPD-SRM只能区分样品是否有故障,不能区分故障的具体类型或程度。当积累了足够多的代表性故障样本时,可以使用KPD-CNN建立多分类模型。

2.2 KPD-CNN有效性

接下来,笔者使用仿真分析验证上述KPD-CNN方法的有效性。

同样,下面笔者对3个案例进行对比分析:

(1)使用传统的CNN分析数据集A(没有多普勒效应);(2)使用传统的CNN分析数据集B(具有多普勒效应);(3)使用笔者所提出的KPD-CNN分析数据集B(具有多普勒效应)。

t-SNE对特征分布的降维可视化,如图7所示。

图7(a)中,利用t-SNE将构建的CNN模型中学习特征可视化为二维。可以看出:案例(1)中不同的故障类别和故障之间有很大的可分性。同一类别的特征聚类良好。测试样本识别率达到100%;

在案例(2)和案例(3)中,数据集B通过KPD-CNN进行测试,分别如图7(b)和图7(c)所示。通过对比图7(a)和图7(b)可以看出,在多普勒效应的影响下,其中4个(第3、5、7、9号)故障类型重叠。这导致分类准确度下降到85%;

从图7(c)可以看出:KPD-CNN的分类准确率提高到96%。

图7 t-SNE对特征分布的降维可视化

各类故障基本完全分类识别。仿真分析结果对比如表3所示。

表3 仿真分析结果对比

从表3中可以发现:(1)在多普勒效应的影响下,如果直接从信号中提取特征进行故障诊断,识别率会显著降低;(2)笔者所提出的参数驱动学习模型能够有效构建信号特征、运动学参数和诊断结果之间的函数关系,识别率分别从90.3%、85%提高到97.5%、96%。

2.3 KPD-CNN优越性

为了进一步验证该KPD-CNN方法的优越性,笔者采用经典的支持向量机(support vector machines,SVM)方法[22]和K近邻(K-nearest neighbors,KNN)方法[23]对上述相同情况进行处理,并将结果进行比较。

笔者构建运动学参数驱动的支持向量机(kinematic parameters drive support vector machines,KPD-SVM)和运动学参数驱动的K近邻(kinematic parameters drive K-nearest neighbors,KPD-KNN);然后,将这两个网络用于处理数据集B(具有多普勒效应),并与笔者所提出的KPD-CNN、传统SVM和KNN的结果进行比较,结果如表4所示。

表4 与其他方法的比较

首先,从识别率的比较可以看到:在不使用3个参数作为输入的情况下,3个网络的识别率分别达到了20.0%、31.7%和85.0%;使用3个参数作为输入后,3个网络的识别率分别提高到了30.7%、44.6%和96.0%。

由此可见,运动参数的输入确实可以有效提高网络的识别率;同时,可以看到采用KPD-CNN的识别率达到了最高;

其次,笔者还比较了3种方法的效率:在使用这3个参数作为输入之前,3种方法的花费时间分别为7.253 2 s、8.971 4 s和72.694 2 s;使用这3个参数作为输入后,这些方法的花费时间分别为8.226 2 s、10.001 2 s和80.987 4 s。

通过对比可以发现：KPD-CNN虽然计算效率相对较低,但是达到了最高的故障识别率。

3 实验验证

3.1 实验装置

为了进一步证明基于参数驱动的学习模型的有效性,接下来笔者通过实验来加以验证。

由于使用真实列车进行实验的高风险和高成本,笔者选择使用仿真实验。

仿真实验的装置和麦克风阵列,如图8所示。

图8 实验装置与麦克风阵列

图8(a)中:实验使用汽车上的扬声器作为轴承声源,通过汽车的高速运动可以实现多普勒效应,可以控制车速来获得不同的声源运动速度信号。实验使用了7种不同速度。利用光电传感器检测前后轮的到达时间,利用前后轮到达的时间差计算出车速。光电传感器的信号也可用于截取信号进行分析。

图8(b)所示的3×5自由场麦克风阵列用于捕获声音信号。实验中选择了4种故障类型的轴承信号作为声源,包括IRF、ORF、RF和Healthy状态。实验中麦克风控制在距离声源运动距离最近的1 m处。

3.2 实验结果与分析

为了方便对比分析,笔者首先使用传统的SRM对不受多普勒效应影响的声源信号进行分析(每种故障类型50个样本,共200个样本)。

在进行特征计算之前,笔者使用带宽为1 kHz～4 kHz的巴特沃斯带通滤波器来消除轮胎噪声、气动噪声等背景噪声;然后选取40个健康样本作为训练样本构建SRM,其余10个健康样本和150个异常样本用于测试。训练后的SRM的最优惩罚参数C为0.1。

在实验分析中训练的SRM的降维可视化图,如图9所示。

图9 在实验分析中训练的SRM的降维可视化图

其中,图9(a)显示了训练后的SRM的降维可视化。测试准确率为97.5%;

然后笔者分别使用SRM和KPD-SRM分析具有多普勒效应的样本,分析的样本对应4种故障,每种故障包含7种速度的30个样本。健康样本总数的80%作为训练数据,其余20%和其他故障类型的630个样本用于测试。训练后的SRM的最佳惩罚参数分别为0.37和0.42;

图9(b,c)显示了构建的SRM和KPD-SRM的视觉结果。可以发现:在多普勒效应的影响下,如果直接使用传统的SRM建模方法,测试准确率从97.5%下降到88%;当使用提出的KPD-SRM方法时,识别率提高到93.5%。

笔者使用实验数据来验证KPD-CNN的有效性。为了比较分析,笔者首先使用CNN对没有多普勒效应的样本进行分析。共分析4种故障类型,每种故障类型100个样本,训练集和测试集样本比例为7 ∶3。

笔者使用t-SNE降维可视化图,如图10所示。

从图10(a)中可以看出:特征的可分性很高,训练模型的识别准确率达到了100%;

然后,笔者使用CNN和KPD-CNN来分析受多普勒效应影响的样本。分析样本共包含840个样本,从样本中随机抽取588个样本进行训练,其余252个样本用于测试。

笔者使用t-SNE降维可视化如图10(b,c)所示。通过比较图10(a,b),可以发现：图10(b)中的不同类型相互重叠,说明在多普勒效应的影响下,可分离性明显降低,导致识别准确率下降到82%;

通过对比图10(b,c)可以发现：图10(c)中的特征可分性得到了明显的提升,识别准确率也提高到了97%。

图10 在实验分析中通过t-SNE对特征分布的降维可视化图

上述不同方法的识别准确率对比结果如表5所示。

表5 实验分析结果对比

通过以上实验分析,进一步证实了多普勒效应对信号特征可分离性的影响,也证实了基于参数驱动的学习模型的有效性。实验方案分析中提出的参数驱动学习模型的识别准确率分别达到了93.5%和97%。

同样,为了进一步验证KPD-CNN方法的先进性,笔者使用仿真方案中提到的另外2种网络结构进行对比分析,结果如表6所示。

表6 与其他方法的比较

首先,由识别准确率的比较可以看到:在不使用3个运动参数作为输入的情况下,3个网络的识别准确率分别达到了72.7%、64.4%和82.0%;使用这3个参数作为输入后,3个网络的识别准确率分别提高到了89.9%、88.9%和97.0%。这再次证明了参数的输入确实可以有效提高网络的识别准确率;同时,也可以看到笔者所提出的KPD-CNN的识别准确率达到了最高;

其次,在使用3个参数作为输入之前,3种方法的构建时间分别为3.621 4 s、6.465 0 s和25.220 4 s。以这3个参数作为输入后,这些方法的构建时间分别为4.974 6 s、7.751 4 s和30.141 6 s。

通过以上实验方案的对比分析,可以进一步证明,虽然KPD-CNN在计算效率上没有优势,但可以达到最高的识别准确率。

4 结束语

在轨边声学检测(TADS)过程中,列车轴承信号由于多普勒效应的影响,会导致其轴承故障诊断准确性下降,为此,笔者提出了一种基于参数驱动学习模型的列车轴承声学智能故障诊断方法。

该学习模型中的第一个模型KPD-SRM用于初始阶段诊断,并积累样本;当积累了足够多的多类代表性数据样本时,用第二个模型KPD-CNN进行故障诊断。为了验证上述模型的有效性,笔者分别采用仿真和实验的方式对其进行了验证。为了验证其优越性,笔者又将其与其他方法进行了对比。

研究结果表明:

(1)仿真分析的故障诊断准确率分别达到97.5%和96%,实验分析的故障诊断准确率分别达到93.5%和97%,因此,可以证明KPD-CNN方法是有效的;

(2)该方法不需要预先信号校正来消除多普勒效应的影响,也可准确地进行故障诊断,这为TADS技术提供了新的思路;

(3)由于机器学习方法的引入,可以利用历史数据来提高诊断准确率,并且准确率会随着监测样本的增加而不断提高;

(4)该方法所采用的安全域技术可以解决工程实践中无法避免的样本不平衡问题,具有良好的实际工程应用前景。

与现有方法相比,KPD-CNN方法无需信号校正,可以解决样本不平衡问题;采用机器学习方法,利用历史数据提高诊断准确率,并且准确率会随着监测样本的增加而不断提高。

在后续的工作中,笔者将继续对上述故障诊断模型进行改进和优化,不断提高故障诊断的精度,并利用实测数据对该诊断方法的有效性进行验证,对算法进行改进。