基于时频域多指标融合和图模型的滚动轴承早期退化监测方法*
桂 伟,陈 鑫,叶新来
(1.武汉商学院 机电工程学院,湖北 武汉 430100;2.山东大学 机械工程学院,山东 济南 250061;3.潍柴动力股份有限公司,山东 潍坊 261199)
0 引 言
滚动轴承作为一种重要的通用机械部件,广泛应用于工业机械中,被称为“工业的关节”[1]。然而随着其使用时间的增加,滚动轴承的性能会逐渐下降。当滚动轴承的退化达到临界水平时,将会形成严重故障,从而导致不可预测的严重后果。
因此,对滚动轴承进行全生命周期的状态监测,以确保其在运行过程中的可靠性和稳定性,对于整个机械设备的安全运行至关重要[2]。
目前,从滚动轴承的振动信号中提取监测指标是进行滚动轴承状态监测的有效手段之一[3]。传统的监测指标有:均方根值(root mean square, RMS)、方差、峰值因子、峭度、偏度等。但振动信号往往涉及复杂的频谱变化、非线性特征等,导致传统指标在检测过程中往往会出现许多错误检测点或遗漏检测点。出现该现象的主要原因是以上指标在处理高噪声和非平稳振动信号时存在固有缺陷。
作为改进的替代方案,许多研究已经将时域统计指标与频谱相结合,从而利用滚动轴承振动信号的固有特性进行状态监测。例如,ANTONI J等人[4]提出了一种应用Spectral kurtosis(SK)来表征滚动轴承非平稳振动信号的方法,同时探索了其在旋转机械故障诊断(振动监测)中的应用[5]。为了更好地描述旋转机械的瞬态故障,ANTONI J[6]提出了一种更快捷的计算方法,称为Kurtogram。
上述改进指标虽然在实际应用中均取得了良好的效果,然而这些指标仍然是联合时频域的一维指标,对旋转机械复杂故障信息的提取仍然不够全面。
另一方面,在滚动轴承复杂的工况条件下,使用单一指标往往会有不同的表现[7]。例如,RMS是分析平稳信号的有力工具,但在分析时变的非平稳振动信号方面受到限制;峭度通常用于检测瞬态冲击,但是难以区分脉冲噪声和循环瞬态冲击,尤其是在信噪比(signal-noise ratio, SNR)较低的情况下。因此,解决采用单一指标时,存在的复杂故障信息提取不够全面的问题,比较直接的方法是采用某种融合技术,将单一指标的有用信息进行聚合,从而得到一个综合指标。
目前,许多数据融合技术被提了出来,并得到了广泛应用。比如,主成分分析、支持向量机、自适应加权融合等。WANG T等人[8]提出了一种通过加权因子将逐点均值和逐点最大值结合的融合方法,并取得了很好的实验效果。但是在数据融合技术使用过程中,其权重因子的确定仍要依赖于SNR,并由经验确定,从而限制了该方法的实际应用效果。
同时,近年来图模型在机械设备状态监测领域得到了广泛的应用。由于图模型在处理数据序列时不需要任何先验知识,同时其能够很好地捕捉信号的长相关性[9],在变化点检测及故障诊断方面取得了优异效果。比如,文新[10]提出了一种将小波分解与图模型相结合的方法,用于轴承的早期故障检测与诊断。WANG T等人[11]提出了一种基于图模型的新时频统计方法,并将其应用于速度与负载变化的检测。
相比于经典的方法,采用上述方法得到的状态检测结果有了显著改善。然而上述方法仍为基于单指标的监测方法,在故障特征提取时仍然可能存在一些遗漏。
基于上述工作,笔者提出一种新的基于时频域多指标融合和图模型的滚动轴承早期退化监测方法,即先从滚动轴承振动信号中提取时频域指标,再采用图模型对其进行优化,吸收噪声;随后对优化后的多指标进行融合,得到综合的监测指标,从而有效提高该方法的实际应用效果;最后,采用XJTU-SY滚动轴承加速寿命试验数据集[12],对该方法进行实验验证。
1 滚动轴承退化点检测方法
1.1 时频域指标提取
振动信号的指标提取是第一步,也是最重要的一步之一。
首先,笔者将原始的振动信号X分为包含相同数据点的多个片段,每个片段内数据近似视为一段平稳信号,即{X1,X2,…,Xn}(其中,n为分段数);在实验中根据实验设置,如采样率等因素确定分段包含的数据点,即滑动窗L的大小(在该实验中,作为先验估计,设置了多个不同的滑动窗长度,即L=1 000,2 000,5 000,10 000,并在实验结果中展示了最佳滑动窗长度的实验结果);原始振动信号分段完成后,从每一分段Xi(i∈1,2,…n)中提取一系列时频域指标,然后将提取的每一个指标按时间顺序重新组合,即可表征滚动轴承的运行状态。
在时域指标中,均值和标准差通常被用作度量具有对称分布的时间序列最有效的特征。其他统计特征也能从不同的角度提供有关时间序列的重要信息,如峭度、RMS和偏度。
因此,在该方法中,笔者选取了常用的{标准差,方差,RMS,最大绝对值,峭度}共5个时域指标。同时,为了保证提取指标全面性,笔者将分段信号进行离散傅里叶变换,计算频率的RMS值,即均方根频率[13]。
综上所述,笔者共提取6个时频域指标,使得原始信号X可以由提取的多个指标来表示,即X=[H(1),H(2),…,H(6)]T。

1.2 图模型指标优化
上述提取到的传统时频域指标,容易受到噪声的干扰,出现错误检测点,或者因轴承早期的微弱变化信息被噪声掩盖,而无法检测到真实的退化点。因此,笔者提出了一种新的基于图模型的方法,来优化每个通道上的单一指标,以克服传统指标在轴承早期退化监测中的缺陷。
由于图模型能很好地体现非平稳信号时序上的相关性,能够增强传统指标的抗干扰和抗噪声能力,笔者采用图模型对提取的时频域指标进行优化,其优势在于:图模型能够有效地捕捉非平稳时间序列的长程相关性,极大地抑制振动信号中存在的非平稳现象;且通过图建模,可以提取单一指标中隐藏的结构和拓扑信息,有助于吸收局部噪声。
典型的图G由一组节点和一组边组成,即G=(V,E),其中:V={v1,v2,…},E={e1,e2,…}。
对第m维单一指标H(m),图建模的过程如下:
(2)在每个数据片段中,将所有数据点视为节点{v1,v2,…,vj},连接每2个节点va和vb得到一组边la,b,其中:a,b∈{1,2,…,j};
(3)计算每个边的权重da,b,da,b为对应于ta和tb的之间的欧几里德距离,即la,b→da,b;
(4)将图模型G表示为邻接矩阵εk,即:
(1)
图建模流程示意图如图1所示。
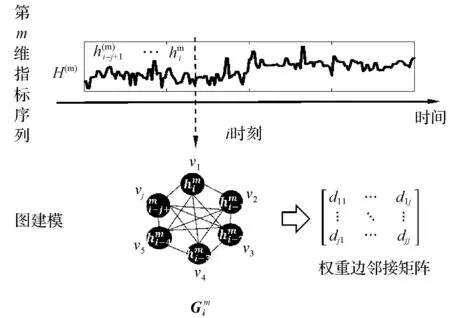
图1 图建模流程示意图
1.3 图模型相似度计算
得到图模型序列后,需要经过动态图模型分析找出异常点。在动态图分析中,需要一个特定的模型来拟合/表征历史图模型。中值图被证明是实现这一目的的重要工具[14]。
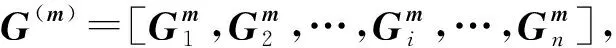
(2)
式中:M(·,·)—图模型距离度量。
该处,笔者使用基于边缘权重值(distance ofedge weight value, DEWV)的方法,即:
(3)
(4)
(5)
为了提高计算效率,笔者使用当前时间节点前的4个图模型来计算中值图。
(6)

1.4 多指标融合
上述得到的相似度分数仍然是相互独立的,因此,需要一个融合方法将独立通道中的信息进行整合,从而得到最后的综合指标。
笔者采用逐点均值和逐点最大值结合的方法进行多维信息融合,其计算过程如下:
由于不同维相似度分数数值差异较大,融合时为了避免较小的数值融合后丢失,出现“大数吃小数”的现象,首先要对相似度分数S(m)采用最大最小归一化处理:
(7)
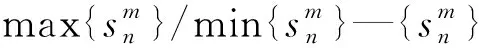
计算逐点均值qavg和逐点最大值qmax:
(8)
(9)
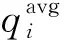
(10)
式中:α—权重因子。
其中:
(11)
式中:σavg—初始化数据{qavg}的方差;σmax—初始化数据{qmax}的方差。
1.5 异常决策
根据上述综合指标{si},笔者使用±kσ准则进行假设检验,通常k取值为3或6。kσ准则以高斯分布为基础,用控制上限和控制下限来定义置信区间。
超出置信区域的点则视为异常发生,即:
H0:正常状态:sn+1∈A
HA:发生异常:sn+1∉A
(12)
式中:A—置信区间。
其中:
A=[μn-kσn,μn+kσn]
(13)
式中:μn—相似度序列的平均值;σn—相似度序列的标准差。
2 状态监测实验及结果分析
2.1 实验设置
笔者采用在滚动轴承状态监测中常用的公开数据集:XJTU-SY滚动轴承加速寿命试验数据集,对所提出综合指标的有效性进行实验验证。
XJTU-SY滚动轴承加速寿命实验台如图2所示。

图2 XJTU-SY滚动轴承加速寿命实验台
该实验台采用交流电机进行驱动,包含2个支撑轴承和1个测试轴承;采用液压装置对轴承进行径向加载,通过加速度传感器采集信号。
XJTU-SY轴承数据集工况及失效类型如表1所示。
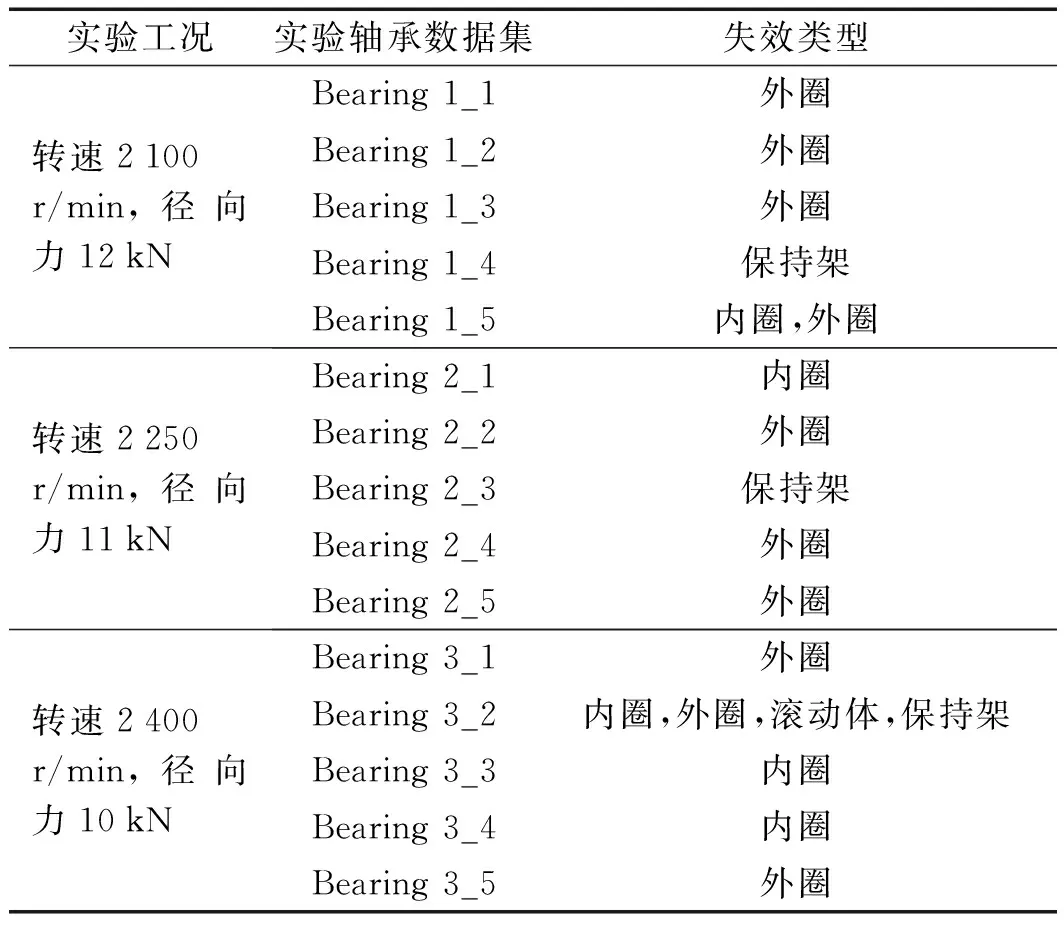
表1 XJTU-SY轴承数据集工况及失效类型
加速退化实验设置了3种工况,分别是:
(1)转速2 100 r/min,径向力加载12 kN;
(2)转速2 250 r/min,径向力加载11 kN;
(3)转速2 400 r/min,径向力加载10 kN。
每种工况下有5个测试轴承,总共采集15组测试数据。测试轴承型号选择LDK UER204型滚动轴承,在被测试轴承的水平和竖直方向,分别安装PCB 352C33型加速度振动传感器,采样频率均为25.6 kHz。
笔者根据以上数据集采样率等实验设置,考虑到不同的数据长度及提高计算效率,将:
bearing3-1,3-2,3-4数据按1 ∶50进行降采样;
bearing1-4,2-1,2-3,2-5及3-3数据按1 ∶10进行降采样;
其余数据,按1 ∶5进行降采样。
滑动窗长度L设置为5 000个数据点,图建模节点数j设置为10,假设检验时k取值为6。
2.2 实验结果与分析
应用上述综合指标,笔者在XJTU-SY数据集的15组测试数据上进行了实验。从检测结果可以看出所提出的方法能够有效地检测到轴承退化点。
XJTU-SY数据集检测结果示例如图3所示。
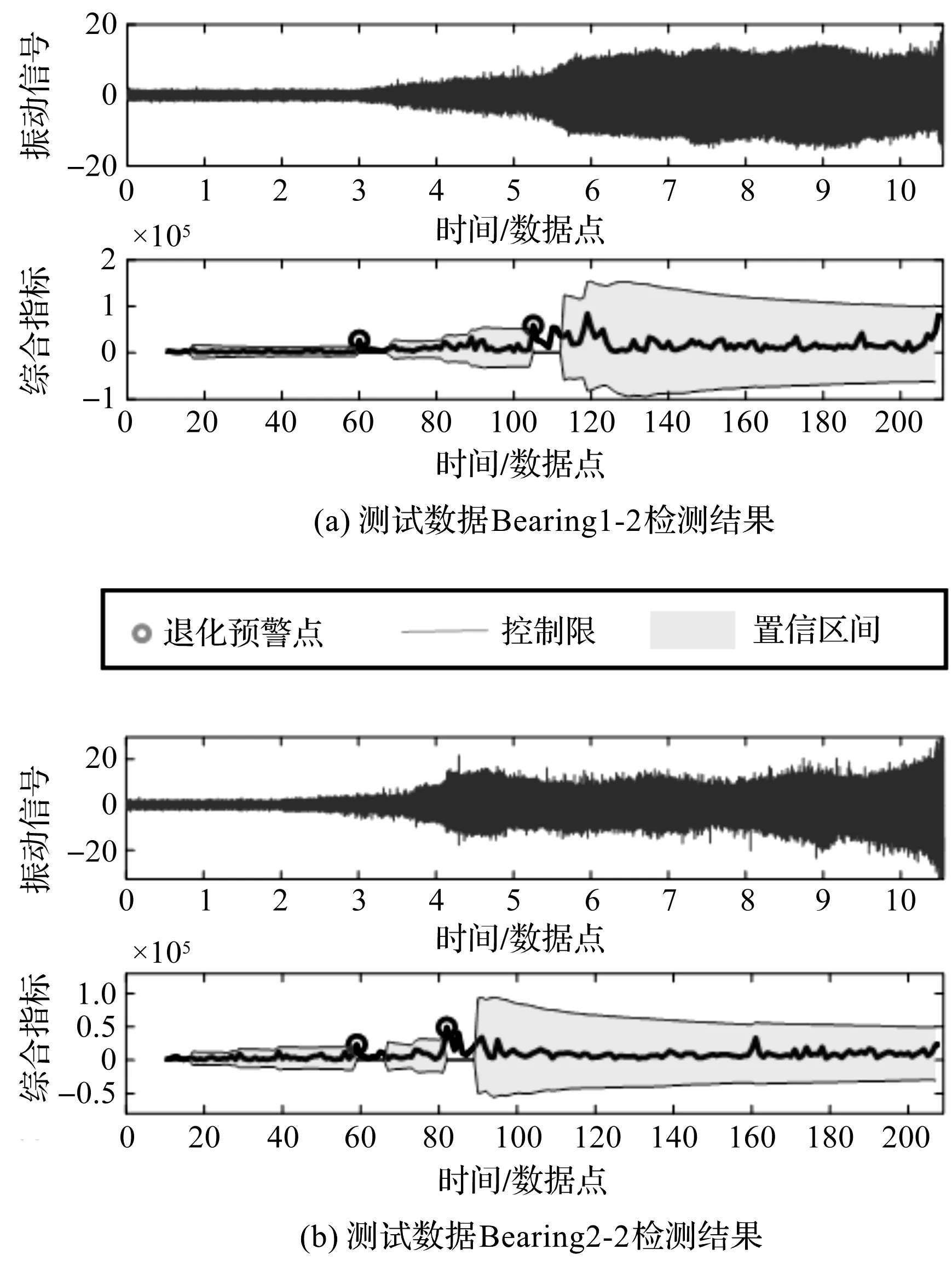
图3 XJTU-SY数据集检测结果示例
轴承的退化是多阶段的,完整的轴承生命周期包括正常、轻微退化、严重退化及失效多个阶段[16];对Bearing1-1,1-2,1-3,1-5,2-2,2-4,2-5和3-5,轴承退化包含多个阶段。
因此,笔者所提方法可以检测到1—2个退化点,可以为有效地为轴承早期性能退化提供预警;但并非所有轴承都会完整地经历多个阶段后失效,如对Bearing1-4,2-1,3-1,3-3和3-4,轴承是突然退化的,笔者所提出的方法能够准确地检测到这些退化点。特别地,对bearing 2-3和3-2,均为缓慢退化的类型,但该方法在检测过程中均出现了一个或多个误报点,以bearing2-3为例,误报点处峭度值出现较大异常值,在指标融合后出现误报点。
峭度对冲击性振动敏感[17],因此,该处可能存在短暂的冲击振动等噪声影响,笔者也将继续探究出现该误报的原因,对该方法进行进一步的改进。
2.3 对比与分析
为了展示综合指标的有效性和先进性,笔者将该综合指标与文献[18]中提出的SES infogram(SESI)进行了比较;同时,还将该综合指标与峭度、RMS、方差等代表性方法进行了比较。
为了量化比较结果,笔者根据排名(method of ranking,MOR)法则[19]对以上方法的检测结果进行排名(排名规则为:误报警点少、检测延迟小的方法排名更高)。显然,综合的平均排名越高,检测效果越好。
对比实验结果如表2所示。
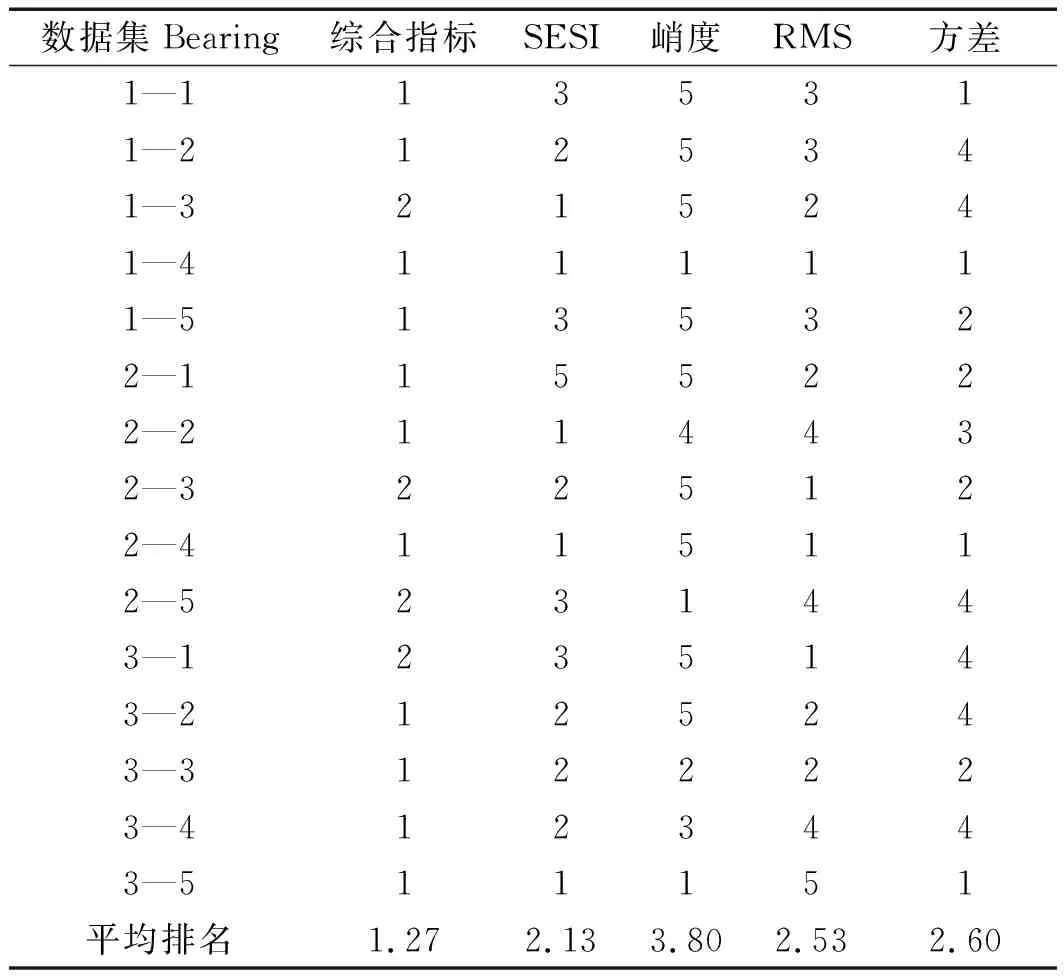
表2 对比实验结果
从对比结果可以看出:基于时频域多指标融合和图模型的方法(即表2中的综合指标)取得了最高的平均排名,证明了该综合指标在轴承退化点检测上的有效性[20]。
3 结束语
在对滚动轴承的全生命周期健康状态进行监测,采用从振动信号中提取监测指标时,存在噪声干扰、检测准确度低的问题,为此,笔者提出了一种基于时频域多指标融合和图模型的滚动轴承退化点检测方法,并通过滚动轴承全生命周期数据集及对比实验,对所提出的综合指标进行了验证。
研究结果表明:
(1)该方法在公开轴承退化数据集上的实验,对每一个测试数据均能成功检测到1—2个退化点,表明该方法通过图模型的优化,提高了传统指标的抗噪声干扰能力,同时多指标融合保证了监测的全面性;
(2)在与其他方法的对比实验中,该综合指标取得了1.27的最高平均排名,体现了所提出方法的先进性,也表明了该方法在实际工程应用中具有良好潜力。
在以后的工作中,笔者将根据实验中出现的误报点进一步优化时频域指标和权重因子,以取得更好的检测效果。

