混凝土深梁腹筋拓扑优化设计

吴大健，周 巍，闵雪峰，张申昕

(1.中交第二公路勘察设计研究院有限公司,武汉 430100；2.河北省高速公路京雄筹建处，河北 雄安 071799;3.武汉理工大学 交通与物流工程学院，武汉 430063)

在城市交通日益复杂、空间受限的情况下，大悬臂花瓶型混凝土桥墩在保证了行车净空与行车视距、增加桥下通透度的同时也保有了结构的曲线美，因此，这一桥墩构造形式在现今得到了越来越多的应用。

对于大悬臂花瓶型混凝土桥墩，顶部的“盖梁”受力特性表现为不再满足平截面假定的深梁复杂受力构件，与适用于传统抗弯理论和抗剪理论的浅梁区别较大。对此类深梁构件，通常使用拉压杆模型反映结构的传力机理并进行结构配束设计，且技术较为成熟。Panjehpour等[1]针对压杆拉杆模型方法计算深梁的极限抗剪强度，完成了仿真与试验的对比研究；仲济涛等[2]推导了考虑预应力效应的深梁极限抗剪承载力公式，提出了主拉应力沿深梁压杆分布的不均匀系数表达式。 准确合理地建立拉压杆模型是应用拉压杆模型进行设计时的重点，中外许多学者在运用拉压杆模型研究复杂应力构件时发现，通过荷载路径及应力迹线来确定复杂应力构件所对应的拉压杆模型较为困难。陈晖等[3]发现复杂应力构件的实际破坏形态与拉压杆模型设计的破坏形态存在差异；Deng等[4]则发现使用拉压杆模型设计复杂应力构件的适用性存在问题。

国内外学者通过运用结构拓扑优化的方法来得到更为符合荷载传力路径的拉压杆模型。Almeida等[5]采用基于位移为优化基准的平滑结构优化算法，并证明其具有一定效果；Seifi等[6]则分别使用过渡截面法和双向进化结构法对深梁结构进行设计优化。张鹄志等[7-8]、刘霞等[9]则利用遗传拓扑优化算法对钢筋混凝土深梁进行了拓扑优化，并进行了相应的试验对比和配筋设计；Zhou等[10]开发了弹性响应捕捉的拓扑优化算法并验证其准确性。但现有结构拓扑优化研究大都忽略了混凝土开裂后的软化现象以及腹筋对钢筋混凝土深梁结构抗剪受力性能的影响，忽略了混凝土开裂后应力重分布对钢筋应力分布的影响[11-13]。目前学者们已经提出基于混凝土的软化现象、腹筋的抗剪作用及相对应的理论模型。潘元等[14]提出了节点等效核心区在剪、压复合作用下的软化桁架模型；马煜东等[15]证明了软化拉压杆模型计算抗剪承载力的有效性。但这些理论模型尚未被应用到钢筋混凝土深梁的拓扑优化及腹筋的配束设计中。

文中通过ANSYS软件的APDL语言进行二次开发，编写相应的钢筋混凝土深梁腹筋的拓扑优化算法，并结合软化拉压杆理论分析优化腹筋对深梁结构抗剪受力性能的影响，完成深梁结构的腹筋配束设计。在此基础上结合花瓶式桥墩盖梁缩尺模型实例，进行腹筋拓扑优化及配束设计并验证其有效性。

1 软化拉压杆理论

如图1所示，软化拉压杆模型由斜向机构、水平机构和竖向机构三部分构成。斜向机构一般为混凝土所构成的斜压杆，而水平机构和竖向机构则由混凝土中相应的水平腹筋或竖向腹筋及其对应的平缓压杆及陡峭压杆组成[16]。

图1 节点软化拉压杆模型

在软化拉压杆模型中，深梁内的水平剪力及竖直剪力与混凝土斜压杆、水平腹筋及竖向腹筋中力的关系可表示[17]为

VQ h=-Fccosθ+Fh+Fvcotθ

(1)

VQ v=-Fcsinθ+Fhtanθ+Fv

(2)

VQ v/VQ h=tanθ

(3)

式中：VQ h为深梁中水平剪力,VQ v为深梁中竖直剪力,Fc为混凝土斜压杆压力,Fh为水平腹筋拉力,Fv为竖向腹筋拉力。

由于深梁中的剪应力由混凝土斜压杆、水平腹筋及竖向腹筋共同承担，因此，需要明确三者所承担剪力的相应比例。根据研究表明，三者之间的剪力承担比例[18]为

-Fcsinθ∶Fhtanθ∶Fv=Cc∶Ch∶Cv

(4)

其中，Cc，Ch和Cv分别为混凝土斜压杆、水平腹筋及竖向腹筋之间力的比例关系，而比例系数的求解则与深梁节点中水平腹筋及竖向腹筋的参与情况相关。下面分别介绍不同的节点受力模式。

1.1 节点剪力由混凝土斜压杆与竖向腹筋承担

当节点处没有水平腹筋或水平腹筋已经受拉屈服时，节点只有混凝土斜拉杆与竖向腹筋来承担剪力时,此时竖向腹筋与竖直剪力比值为

(5)

而该比值的范围则是由混凝土斜拉杆的角度来决定:当混凝土斜压杆的角度较小时，混凝土斜压杆对竖向剪力的承担可以忽略不计，此时认为节点处的竖向剪力全部由竖向腹筋承担;当混凝土斜压杆的角度较大时，则认为节点处的竖向剪力全部由混凝土斜压杆来承担。

1.2 节点剪力由混凝土斜压杆与水平腹筋承担

同样，当节点处的竖向腹筋已经受拉屈服时，节点处的剪力只由混凝土斜压杆及水平腹筋来承担，此时水平腹筋与水平剪力比值为

(6)

在确定γv与γh后，即可计算Cc、Ch和Cv

(7)

(8)

(9)

则相应的混凝土斜压杆、水平腹筋及竖向腹筋各自力分别[19]为

(10)

(11)

(12)

而节点的破坏可认为是核心区混凝土达到其极限抗压强度导致的破坏，则有

(13)

式中：σd,max以受压为正，θf和θs分别为平缓压杆、陡峭压杆与水平轴的夹角。

根据图2中的几何关系，2tanθf=tanθ=(1/2)tanθs, 则式(13)可变换为

(14)

图2 混凝土压杆力分析

2 基于软化拉压杆理论的腹筋拓扑优化算法

2.1 基于软化拉压杆模型的腹筋优化思路

由上文软化拉压杆模型的介绍可知，结构中的水平腹筋及竖向腹筋与不同方向的混凝土组成水平机构或竖直机构，共同承受混凝土中的剪应力。因此，可以基于软化拉压杆理论，在ANSYS中建立钢筋混凝土有限元模型，分别采用Link10单元与Solid65单元来模拟钢筋与混凝土，其中Link10单元设置为只承受轴向拉应力的杆单元来模拟腹筋，与软化拉压杆模型中的腹筋受力模式刚好相符。同时，可以很好地区分被优化的腹筋单元对象与混凝土单元。由于软化拉压杆模型为开裂混凝土的抗剪受力模型，因此,在ANSYS中需要考虑混凝土开裂情况的模拟，而 Solid65单元作为具有开裂特性的实体单元，可以通过设置开裂后的剪力传递系数，同时假定裂缝在单元内部发生，且产生裂缝之后的混凝土仍然保持连续，则能够较好地模拟腹筋拓扑优化所需情况。

2.2 腹筋拓扑优化算法的舍弃标准

在腹筋拓扑优化中舍去了对结构抗剪贡献较小的腹筋单元，所以需要设置腹筋单元的舍弃标准，再根据舍弃标准进行腹筋单元的舍去或保留。比较合适的标准为腹筋单元的拉应力或是应变能，选取腹筋单元拉应力作为舍弃标准时，优化目标较为明确，可以很直观地反映腹筋单元与混凝土斜压杆共同参与抗剪作用的多少，但不能较好地反映结构的整体状态，不利于整体的腹筋步骤优化及后续拓扑优化收敛的判断，因此，选择结构整体单元的平均应变能作为舍弃标准。在腹筋拓扑优化过程中，通过ANSYS的生死单元法杀死抗剪贡献较小的腹筋单元，会使得整个结构的平均应变能发生变化，所以，在优化过程中通过保证杀死的腹筋单元对整体结构的平均应变能影响较小，即可达到腹筋拓扑优化目的。

下面对杀死腹筋单元后结构整体的平均应变能变化量进行推导，在有限元计算中，每个单元刚度与位移的乘积为单元荷载

F=Ku

(15)

式中：K为有限元单元的刚度矩阵，u为单元位移向量。

由此计算得到荷载势能

(16)

式中：F为荷载向量。

根据荷载势能的计算公式，将荷载势能代入平均应变能算式中可得

(17)

假定结构的荷载恒定，与单元变量无关，通过对荷载在单元变量i上求导，则有

(18)

将结构的平均应变能公式对单元变量i求导，并将荷载对单元变量的求导算式联立，最终得到

(19)

在拓扑优化过程中只舍弃腹筋单元，而舍弃腹筋单元对结构整体重量变化很小可以忽略不记。同时因为混凝土单元并不是拓扑优化对象，在整个拓扑优化过程中混凝土重量不发生变化，因此忽略结构自重的变化，只考虑外部荷载对结构产生的影响，舍弃腹筋单元变量i后，结构整体的平均应变能变化量为

(20)

2.3 腹筋拓扑优化收敛指标

(21)

(22)

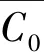
根据前文所述，可以将给第i次拓扑优化后的结构转换平均应变能与初始转换平均应变能作为第i次拓扑优化的优化性能指标Rp，对腹筋拓扑优化的效果进行评价得

(23)

将式(21)～(22)代入式(23)中，可得

(24)

由弹性力学假设可知钢筋混凝土结构为密度均匀的单元，因此可通过体积与重量之间的线性关系将式(24)化简为

(25)

式中:V0为初始优化前结构整体体积,Vi为第i次优化后结构整体体积。

设定了优化性能指标Rpi后，可以根据控制优化性能指标小于设定值来控制腹筋拓扑优化的中止，为避免计算浮点数的影响，一般可以设定优化性能指标在0.90～0.95之间，优化性能指标达到预设值时腹筋拓扑优化结果即为最终的拓扑优化结果。若腹筋拓扑优化未终止，而是在达到预设的拓扑优化次数后停止，则可以通过查询每次拓扑优化后的Rpi值，来寻找最优的腹筋拓扑优化结果。同时考虑更改循环次数的设定以及结构的荷载边界，当结构荷载较小时，有可能因为单元应变能较小而难以迭代至最优解，所以需要对施加的荷载进行预先试算，以保证腹筋的拓扑优化能最终得到最优结果。

2.4 腹筋拓扑优化流程

在模型建立完成后对结构进行加载，并对钢筋混凝土深梁结构施加荷载及约束边界，进行静力分析，在计算完成后进行ANSYS后处理中提取所有结构单元的平均应变能并根据每个单元对平均应变能的影响进行排序，对平均应变能影响较小的腹筋单元说明对结构整体荷载变化的响应较小，因此这部分腹筋单元并不是需要在钢筋混凝土深梁结构中进行配置的腹筋单元。在ANSYS中通过生死单元法杀死影响度排名靠后的一部分腹筋单元并将其进行完全约束，以避免其对剩余结构的整体产生影响，计算此时的优化性能指标Rpi以及被杀死的腹筋单元，将其存储在文本中。然后选择剩余仍存活的混凝土与钢筋单元再次进行静力分析，重新提取所有存活单元的应变能，并对腹筋单元进行影响度排序，杀死排名较后的腹筋单元并约束，再计算优化性能指标及杀死单元。不断重复上述的腹筋拓扑优化流程，直至优化性能指标达到了预设值或达到设定的优化次数，此时停止结构优化，根据记录的优化性能指标选取最优的腹筋拓扑优化结果，此时仍存活的腹筋即为花瓶式桥墩结构中必要配置的水平腹筋及竖向腹筋。钢筋混凝土深梁腹筋拓扑优化流程如图3所示。

图3 钢筋混凝土深梁腹筋拓扑优化流程

2.5 结构优化计算方法验证

为验证腹筋拓扑优化算法的有效性，采用有限元软件ANSYS APDL语言对2.4节中的腹筋拓扑优化流程进行二次开发编程，选取贺华军完成试验中的双开洞深梁进行拓扑优化，并与其荷载试验的破坏开裂结果进行对比。

双开洞深梁的混凝土弹性模量E=30 GPa，泊松比v=0.2；左边支座为铰支座，右边支座为滚轴支座，两支座宽度均为120 mm；集中荷载的数值为200 kN，集中荷载加载点宽度为180 mm。建立钢筋混凝土耦合模型并进行结构优化计算，对该优化方法进行验证，最终得到优化腹筋单元(见图4)。

图4 验证模型优化结果(单位：cm)

由试件裂缝图及拉压杆模型可以看出，该试验构件在洞口上方及构件下方为主拉应力区域，而腹筋最终的拓扑优化结果在洞口上方、洞口下方及构件下方保留了水平腹筋以分担拉应力，而在两个洞口之间的区域主要为压应力的传力区域。同时传力路径较为倾斜，因此该区域主要保留了竖向腹筋，并与混凝土组成竖直机构来抵抗受力，在洞口两侧同样存留了竖向腹筋，在荷载加载下方及支座上部区域传递路径较为平缓，此处主要保留了水平腹筋。因此，基于软化拉压杆模型的腹筋优化算法能很好地根据结构实际传力路径及应力分布保留主要的关键腹筋，从而为腹筋设计提供依据。

3 花瓶式桥墩盖梁纵向钢束配筋设计

京雄高速花瓶式桥墩盖梁缩尺试验模型配筋依据应变相似比及配筋率相同原则[20]，根据原型桥墩的配筋设计拟定，因此，其水平及竖向腹筋是根据构造要求及裂缝控制要求进行配置。在验证混凝土深梁腹筋拓扑优化程序后，文中选取京雄高速花瓶式桥墩的盖梁缩尺试验模型进行腹筋拓扑优化及配束设计，并与缩尺模型的原配束设计进行对比。

3.1 缩尺模型尺寸

花瓶式桥墩盖梁缩尺模型(见图5)短边尺寸为64 cm，长边尺寸为850 cm，高100 cm，缩尺模型采用C40混凝土，容重γ=4×25 kg·m-3。缩尺模型的自重将以均布荷载的形式施加在结构上，而花瓶式桥墩在施工过程中，荷载工况的缩尺荷载将以集中荷载的形式加载在缩尺模型顶面的6个集中荷载加载点上，加载位置分别为a1=2.75 m、a2=7.95 m、a3=14.5 m，集中荷载加载值为50 kN。

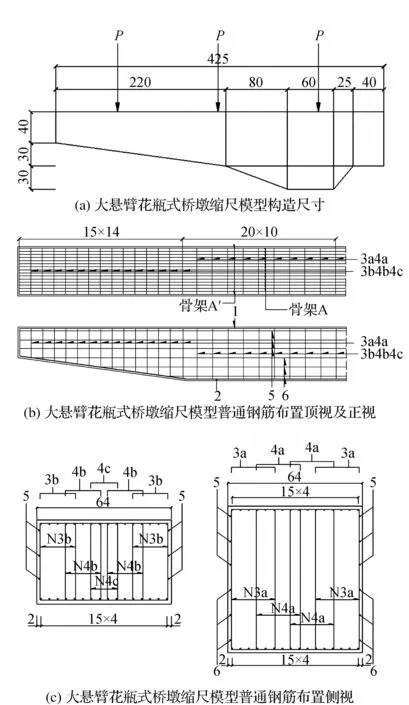
图5 大悬臂花瓶式桥墩缩尺模型构造尺寸及普通钢筋布置(单位：cm)

3.2 有限元模型建立

为充分考虑混凝土开裂后的软化现象以及非线性特性，在ANSYS中选取多线性随动强化KINH模型[21]来定义混凝土材料的应力-应变关系，对应的应力-应变曲线如图6所示。

图6 混凝土应力-应变曲线

在ANSYS中分别建立花瓶式桥墩盖梁缩尺模型的钢筋混凝土单元与腹筋单元网格(见图7)，建立的初始待优化的每片腹筋网格如图7(b)所示，遍布整个盖梁侧面平面上，在盖梁横向方向上如图7(c)所示设置两片腹筋网格，分别位于混凝土单元模型的两侧，然后根据腹筋网格对盖梁混凝土单元进行映射网格划分，并耦合钢筋单元节点与混凝土单元节点，以保证两者之间的相互作用。

3.3 花瓶式桥墩盖梁腹筋配束设计

在建立了如图7所示的钢筋混凝土耦合的盖梁有限元模型后，按照前文所述的钢筋混凝土深梁拓扑优化程序对有限元模型循环地进行静力计算及腹筋单元舍去，设置最大的拓扑优化次数为50次，设置每次拓扑优化舍去当前箍筋中20%影响度较低的箍筋单元，当结构优化性能指标Rp=0.95时停止腹筋拓扑优化。最终在第35次腹筋拓扑优化时达到最优解，最终得到优化结果(见图8)。

如图8所示，图8(a)为初始的腹筋网格，图8(b)为结构优化计算后最终保留的腹筋，下面结合盖梁的拉压杆模型及应力流进行配筋优化结果分析，如图8(c)所示。在盖梁的上部及跨中区域主要分布主拉应力，而在这些区域，结构优化计算最终保留了水平腹筋来承受拉应力。在盖梁变截面段的下部区域主要为角度平缓的压杆，因此腹筋拓扑优化结果也保留了水平腹筋作为水平机构来承担压应力。在荷载之间存在着拉杆及压杆来传递力流，这些杆件的角度较为倾斜，因此在这些区域结构优化结果也主要保留了竖向腹筋来作为竖直机构承担受力。由以上分析可知，拓扑优化后保留的盖梁腹筋基本符合盖梁缩尺模型的受力及传力路径。下面基于该优化结果对缩尺模型腹筋进行设计，最终得到缩尺模型的优化设计配筋(见图9)。

图7 钢筋混凝土耦合模型

图8 腹筋结构优化计算结果

如图9所示，优化配筋在腹筋的配置上，对竖向腹筋及水平腹筋都进行了相应设计调整。水平腹筋根据优化结果增大了水平腹筋间距，减小了水平腹筋的配筋数量，保证结构承载能力的同时节省钢筋数量。竖向腹筋则不同于缩尺配筋的两段式设计，在优化设计结果保留竖向腹筋的区域对竖向腹筋进行加密，而在不保留竖向腹筋的区域依照构造设计配置竖向腹筋，由缩尺模型配筋的两段式设计更改为三段式设计。

3.4 优化模型及原型桥墩对比

在确定优化配筋后，分别建立缩尺配筋及优化配筋的ANSYS有限元模型。混凝土使用SOLID65单元，缩尺模型的普通钢筋使用SOLID65的实常数进行配筋率模拟，优化模型的下弯受拉钢筋使用LINK10单元建立进行模拟，其它钢筋同样使用配筋率进行模拟，最终建立的有限元模型如图10所示。

图9 缩尺模型优化配筋结果

图10 优化模型有限元模型及加载边界条件

图11 缩尺模型及优化模型荷载-应变曲线

对缩尺模型及优化模型分别进行结构分析，绘制荷载-应变曲线(见图11)。

由图11可知，优化模型与缩尺模型的开裂荷载和极限荷载基本相同，但缩尺模型开裂后刚度明显减小，而优化模型在开裂后可以维持结构的刚度，在同样承受130 kN荷载时优化模型的应变要小于缩尺模型的应变，在ANSYS中查看缩尺模型及优化模型裂缝(见图12)。

图12 缩尺模型及优化模型裂缝分布

由图12可知，优化模型的裂缝发展区域要小于缩尺模型的裂缝发展区域，斜向受拉钢筋及腹筋的加密配置抑制了裂缝发展，使得结构在开裂后维持了承载能力，提高了结构耐用性。

4 结 论

1)基于软化拉压杆理论，提出了通过ANSYS APDL语言二次开发的钢筋混凝土构件的腹筋拓扑优化方法，能够较为准确地分析出结构在开裂状态下对结构抗剪贡献较大的水平腹筋及竖向腹筋，为腹筋配束设计提供参考依据。

2)利用提出的腹筋拓扑优化方法对双开洞深梁进行了腹筋拓扑优化，拓扑结果很好地反映了结构实际实验中传力路径及应力分布，保留了关键受力部位的腹筋。

3)基于软化拉压杆理论对花瓶式桥墩盖梁缩尺模型进行了腹筋拓扑优化，并基于腹筋拓扑优化结果进行了缩尺模型的腹筋配束设计，优化配束设计在减少了配置腹筋数量的同时，其极限荷载与原配束设计基本相同。同时，优化配束设计使得在开裂后可以继续维持结构刚度，优化设计后的腹筋也很好地抑制了裂缝发展，提高了结构的耐用性。