斜拉桥覆冰拉索涡激振动数值模拟

张义昌，王贵春

(1.郑州大学 土木工程学院，郑州 450001；2.中国建筑第八工程局有限公司，上海 200135)

在寒冷的冬季，斜拉索表面会形成一层覆冰，覆冰会改变斜拉索的截面形状，从而对斜拉索的涡激振动产生重要影响。近年来，国内外学者对不同截面形状拉索的涡激振动进行了研究。

Cantwell等[1]用实验方法研究了圆柱体阻力系数与雷诺数Re的关系，指出在Re=3 900时阻力系数均值在0.88～1.08之间。Raghavan等[2]通过研究Re=2×104～6×106高雷诺数下圆柱体涡激振动，发现圆柱体的涡激振动在高、中和低雷诺数情况下差别较大。王贵春等[3]基于重叠网格法分析了斜拉索的涡激振动，指出高质量比和低质量比圆柱体涡激振动存在明显差异。

Zhu等[4]通过数值模拟研究了Re为100和200时三角形截面柱体的涡激振动，发现当风攻角为60°时，在Re=100情况下，柱体以涡激振动为主；在Re=200情况下，振动形式为涡激振动与驰振的组合。与相同条件下的圆形截面柱体相比，三角形截面柱体的振动响应更为剧烈。李小超等[5]通过数值模拟研究了圆形、方形、梯形和T字形截面柱体的涡激振动，发现圆形截面柱体振动表现为典型的涡激振动，具有明显的自限特性。其他截面柱体的振幅随流速增大而增大，除了方形截面柱体没有出现明显的漩涡脱落之外，其他截面柱体尾涡脱落均呈现 2S 模式。

Bai等[6]通过风洞试验和数值模拟方法研究了宽高比为9.05～11.96的π形截面复合桥面板的涡激振动，发现宽高比的增加会延迟涡激振动的起始风速。在扭转和横风向振动频率较低的情况下，存在横风向振动和扭转振动共存现象，而宽高比过大时，两种振动则不会同时存在。宋立群等[7]研究了斑海豹胡须的涡激振动，对比了具有相同等效直径的圆形和椭圆形截面胡须在雷诺数Re=300时的振动响应。发现圆形和椭圆形截面胡须的位移-速度相轨均为闭合圆环，动力响应是周期性的，但椭圆形截面胡须的振幅比圆形截面胡须的振幅小。

上述研究表明，柱体的截面形式对涡激振动有明显影响。覆冰拉索的截面形状较为复杂，为便于研究，国内外学者根据覆冰截面形状进行了简化和分类，主要分为新月形覆冰、扇形覆冰和D形覆冰3类。覆冰改变了拉索截面的形状，进而影响结构的涡激振动,国内外学者对此进行了一系列研究。

Koss等[8]利用试验对圆柱体结冰的形状进行了研究与总结，为研究覆冰拉索振动提供了截面参考信息。Demartino等[9-10]对覆冰导线及覆冰拉索振动进行了研究，结果表明覆冰拉索与覆冰导线驰振原理虽然相近，但覆冰拉索与覆冰导线驰振力系数相差很大。

Cao等[11]通过风洞试验研究了不同覆冰厚度下拉索的横风向和扭转振动，发现随着覆冰厚度增加，横风向和扭转振幅增大。Górski等[12]通过风洞试验研究了覆冰拉索在Re=2.5×104～1.36×105范围内的升阻力系数变化规律，并与无覆冰拉索的情况进行了对比，发现其升阻力系数受雷诺数变化的影响更为明显。

蔡萌琦等[13]通过风洞试验和数值模拟方法研究了扇形覆冰八分裂导线的驰振特征。结果表明，风速对驰振水平幅值的影响较垂直幅值更明显，且随着风速增加，导线的振动轨迹逐渐由椭圆转变成圆。Raeesi等[14]选择了9个具有代表性的冰壳模型，通过风洞试验研究了冰壳表面纵横比、曲率和厚度对冰壳的空气动力和力矩的影响，发现其中纵横比对气动力和力矩系数的影响最大，冰壳曲率的影响次之，厚度的影响最小。谭冬梅等[15]对扇形串列覆冰拉索尾流驰振进行了研究，总结了不同索距情况下的下游索驰振稳定性。

上述对覆冰拉索涡激振动的研究以试验为主。文中采用数值模拟方法对具有新月形和D形截面的覆冰拉索进行涡激振动分析，计算其在不同约化风速下的升阻力系数和横风向振幅，分析覆冰拉索的涡激振动规律。

1 数值模拟

1.1 流体控制方程

流体控制方程包括质量守恒方程、动量守恒方程和能量守恒方程。文中模拟覆冰拉索的涡激振动，空气近似为不可压缩流体，热交换量相对很小，可以忽略，故不考虑能量交换。仅考虑质量守恒方程和动量守恒方程，其表达式分别为

(1)

(2)

式中：u,v,w为x、y和z方向的流体速度分量；ρ为流体密度；ω为不同方向的速度；F为不同方向的面力；μ为动力黏度；p为流体介质微元体上所受的压力。

1.2 Rigid Body法

拉索的涡激振动属于流固耦合问题。模拟该类问题主要有Workbench+CFX法、FLUENT动网格法和Rigid Body法等，其中Rigid Body 法是一种有效且新颖的方法，整个系统是由刚性圆柱体、弹簧和阻尼器组成，分别采用线性动量求解器和角动量求解器求解平移和旋转运动。与其他方法相比，Rigid Body法具有计算简便、节约机时等优点，因此，文中使用该方法进行模拟分析。

1.3 几何建模和网格划分

分别建立新月形和D形截面覆冰拉索模型，分析其涡激振动。拉索参数选自参考文献[16],直径为151 mm，自振频率为0.545 Hz，阻尼比取0.03。新月形覆冰最大厚度为10 mm，D形覆冰最大厚度为30 mm, 如图1所示，斜线部分表示覆冰层。

图1 覆冰厚度

设D为拉索直径，计算流体域尺寸为长44D、宽22D、高0.02 m，拉索轴心至入口的距离为11D,距流体左右边界为11D，如图2所示。网格模拟对计算精度和时间有很大影响。鉴于拉索附近区域参数变化梯度大，对其网格适当加密；而对远离拉索的区域，为节省计算时间，取较稀疏的网格。网格划分如图3所示。边界条件定义如下：流体域入口(Inlet)的边界条件，只考虑x方向的速度，即U=U0，V=0，W=0；流体出口(Outlet)的边界条件，考虑风的脉动作用，相对压力设置为0；流体域上下边界条件定义为滑移壁面(Free Slip Wall)，壁面剪切力设为0，流体在近壁处的速度将不受壁面摩擦力的影响；流体域前后面定义为对称边界条件，也即流场前后面对称；圆柱面定义为无滑移壁面条件(No Slip Wall)，模拟近壁处速度为0。

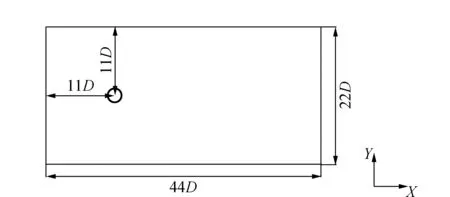
图2 流体区域尺寸

图3 网格划分

2 无量纲参数

为便于计算，引入常用的无量纲参数。

雷诺数Re：流体力学中表征黏性影响的相似准则数，其表达式为

(3)

式中：ρ为流体密度，U0为流体速度，D为拉索外径，ν为流体的动力黏性系数。

质量比m*：表示固体质量与固体所排开流体质量的比值，表达式为

(4)

式中：m为缆索单位长度质量。

阻尼比ξ：结构的阻尼系数c与临界结构阻尼系数之比，表达式为

(5)

式中：c为结构阻尼系数，k为弹簧刚度，ωn为结构的自振圆频率。

Strouhal数：圆柱体的振动频率与旋涡的脱落频率有关，但理论上求解旋涡脱落频率十分困难，因此在实际工程中一般用Strouhal数表示旋涡脱落频率，表达式为

(6)

式中：fs为旋涡脱落频率。

约化风速：表示结构振动一个周期内的流体路径与结构特征尺寸的比值，是流速的无量纲化参数，表达式为

(7)

式中：fn为结构的自振频率。

静风系数：又称升阻力系数，是升力与阻力经过无量纲化得到的相似准则数，表达式为

(8)

(9)

式中：FL为结构所受垂直于风向的力，又称升力；FD为结构所受平行于风向的力，又称阻力；CL为升力系数；CD为阻力系数。

无量纲位移：为覆冰拉索横风向振动位移Y与拉索直径D的比值，表示为Y/D。

文中主要研究拉索横风向振动响应。如无特殊说明，以后提到的振动位移均为覆冰拉索横风向振动位移。

3 实例计算与分析

选用k-ωSST湍流模型。在分析覆冰拉索涡激振动前，选取参考文献[17]的数据，对无覆冰圆柱体绕流进行数值模拟，验证用该模型分析涡激振动的有效性。圆柱体直径为0.1 m，流体速度为0.219 m·s-1，空气流体密度ρ=1.225 kg·m-3，动力黏度为1.7894e-5kg·(m·s)-1, 雷诺数Re=1 500。气动力系数时程曲线如图4所示。

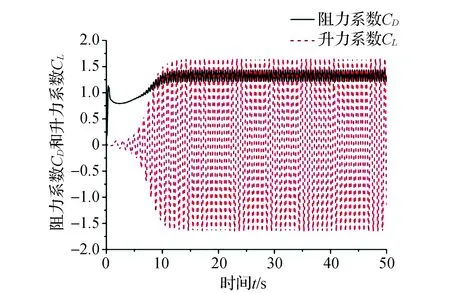
图4 圆柱绕流气动力系数时程曲线

由图4可知，气动力系数振幅在13 s左右达到稳定状态,与此同时，流场也达到稳定状态，出现有规律的旋涡脱落，升阻力系数也达到最大值。它们在相同时间达到最大值与旋涡脱落规律有关。

圆柱上下两侧各泄涡一次，升力完成一个周期的波动，阻力完成两个周期的波动。观察圆柱的升力系数时程曲线，可知振动达到平稳后，升力系数也渐渐趋于平稳，稳定后的升力系数最大值为1.639。

图5 升力系数频谱分析

图5是对升力系数进行傅里叶变换得到的频谱图。由图5可知，泄涡频率为0.435 Hz，计算可得Strouhal数为0.198。把数值模拟得出的平均阻力系数和Strouhal数与国内外已有的结果对比(见表1)。

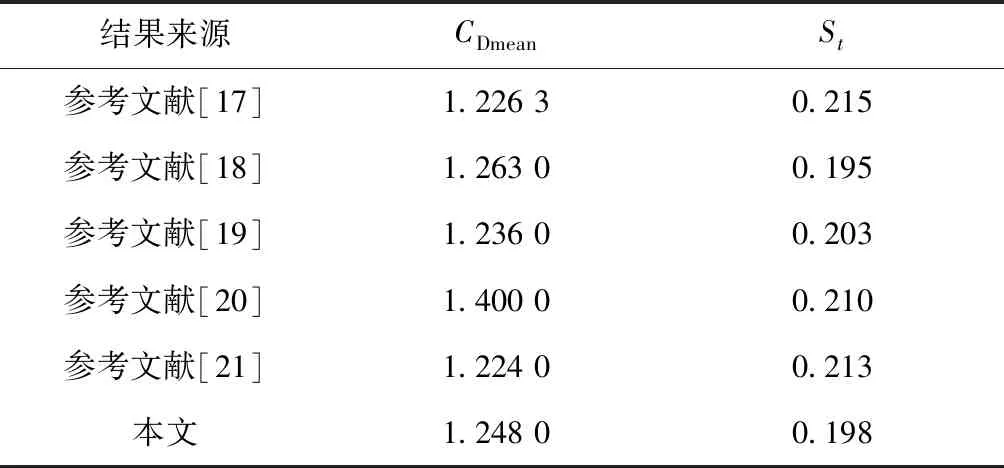
表1 结果对比

由表1可知，文中的计算结果与国内外其他研究结果相差不大，可以使用k-ωSST湍流模型模拟拉索的涡激振动。

3.1 新月形覆冰拉索涡激振动分析

已有试验结果表明，新月形覆冰拉索在Ur=3～7时产生明显的涡激振动，因此在计算中取上述Ur值。图6为升阻力系数随约化风速变化的关系曲线。升力系数取一段稳定时间内的最大值，记作CLmax；阻力系数取一段稳定时间内的平均值，记作CDmean。

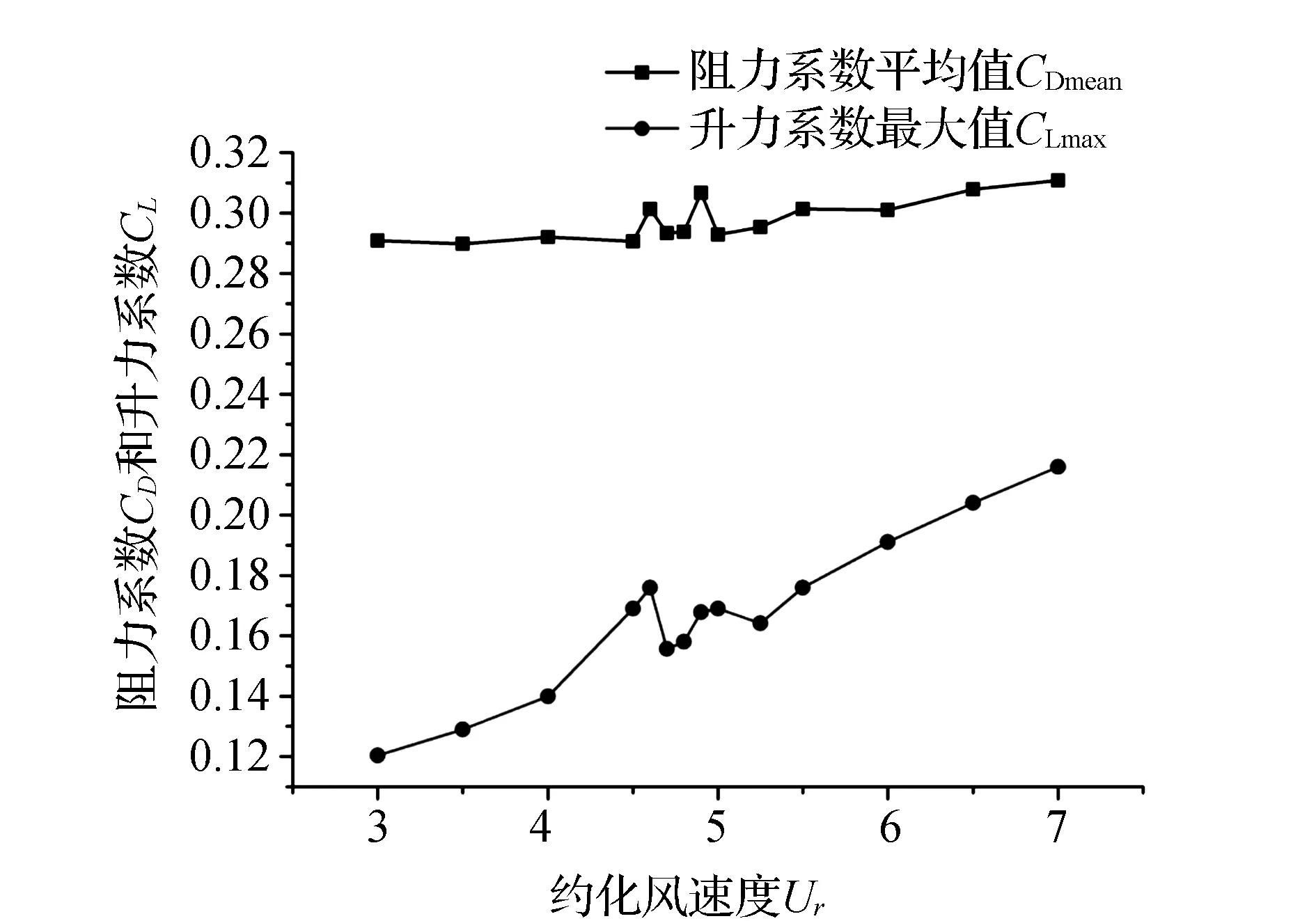
图6 升阻力系数随约化风速变化曲线

由图6可知，阻力系数曲线分为三段:当3≤Ur≤4.5时，阻力系数稳定在0.29左右；当4.5

3.1.2 振动响应分析

图7给出了当Ur=3～7时新月形覆冰拉索的无量纲位移时程曲线。由图7可知：当Ur=4.5时，振动位移开始出现“拍”的现象，这种现象是由于结构振动影响旋涡脱落引起的；当约化风速Ur在5.5～6之间时，“拍”的现象较为明显，说明结构振动在这个风速区间对结构泄涡频率影响较大；当Ur=6.5时，“拍”的现象不再明显，说明结构振动对泄涡影响已经减弱。

图7 不同约化风速下振动位移时程曲线

图8表示新月形覆冰拉索最大位移随约化风速变化的曲线。由图8可知：当Ur≤4.5时，新月形覆冰拉索位移振幅变动相对平稳；当Ur>4.5时，振幅逐渐上升；当Ur=5.25时, 振幅达到最大值0.057, 随后急剧下降；当Ur>6时，振幅趋于平稳。

图8 振幅随约化风速变化曲线

3.2D形覆冰拉索涡激振动分析3.2.1 升阻力系数分析

图9表示D形覆冰拉索升阻力系数随约化风速增加而变化的关系曲线。由图9可知，阻力系数曲线比较平稳，其值在0.35上下微小波动。升力系数的变化分为3个阶段：当3≤Ur≤6.5时，随着约化风速增大而增大；当6.5

图9 升阻力系数随约化风速变化曲线

3.2.2 振动响应分析

图10给出了D形覆冰拉索在Ur=3～10时的无量纲位移时程曲线。由图10可知，当Ur=5.5时，振动位移响应逐渐出现“拍振”现象，比起新月形覆冰拉索的情况，D形覆冰拉索发生‘拍振’现象所需临界风速更大。随着约化风速的增加，D形覆冰拉索“拍振”现象的特征逐渐加强，当Ur=6.5时最为明显，然后逐渐减弱，持续到Ur=10。也即在Ur=5.5～10之间时振动频率对结构泄涡频率有锁定作用。

图10 不同约化风速下振动位移时程曲线

图11表示D形覆冰拉索最大位移随约化风速增加而产生变化的曲线。由图11可知：当Ur≤5.5时，新月形覆冰拉索位移振幅相对平稳；当Ur>5.5时，振幅逐渐增大；当Ur=7.25时,达到最大值0.447,随后急剧下降；当Ur>8.5时，振幅趋于平稳。

图11 振幅随约化风速变化曲线

图12 3种情况计算结果对比

3.3 对比分析

比较3.1.1和3.2.1中的升阻力系数，可以发现，在涡激振动的各个阶段，D型覆冰拉索的升阻力系数均大于新月形覆冰拉索的情况。拉索的振动位移与升阻力系数成正比。图12给出了两种覆冰拉索的涡激振动位移振幅以及陈文礼等[22]研究的无覆冰拉索涡激振动位移振幅随约化风速变化曲线。由图12可知，新月形覆冰、无覆冰和D形覆冰拉索的最大位移振幅分别为0.057、0.095和0.45，其相对应的约化风速分别约为5.25、6和7.25。比较新月形覆冰拉索与无覆冰拉索的最大位移振幅，前者只是后者的60%；比较D形覆冰拉索与无覆冰拉索的最大位移振幅，前者是后者的4.74倍。上述分析表明，D形覆冰拉索的最大位移振幅最大，无覆冰拉索的情况次之，新月形覆冰拉索的最大位移振幅最小，且产生上述最大位移振幅时对应的约化风速也依次减小。新月形覆冰对拉索振动有一定的抑制作用，D形覆冰对拉索振动有一定的放大作用。其主要原理在于拉索有新月形覆冰后，其整体截面形状更趋于流线型，对流体扰动减小，从而使缆索的振动减弱；而拉索有D型覆冰后，其整体截面形状更趋于非流线型，对流体扰动增大，从而使缆索的振动增强。

4 结 论

1)新月形和D形两种截面形式的覆冰拉索在一定的约化风速下发生涡激振动，并在一定条件下振幅达到最大值。约化风速继续增大，振幅急剧下降。

2)新月形和D形覆冰拉索发生涡激振动的约化风速范围不同。新月形覆冰拉索在Ur=4.5～5.5之间发生涡激振动；D形覆冰拉索在Ur=6.5～8之间发生涡激振动。在一定的约化风速条件下，覆冰拉索的涡激振动会出现“拍振”现象。

3)对比新月形、D形和无覆冰拉索的涡激振动振幅，发现D形覆冰拉索的振幅最大，无覆冰拉索的情况次之，新月形覆冰拉索的最大振幅最小，且上述最大振幅对应的约化风速也依次减小。这说明新月形覆冰对拉索振动有一定抑制作用，D形覆冰对拉索振动有一定放大作用。