基于Hankel-DMD的城市交通事故风险时空预测*

金杰灵，史晨军，邓院昌

(1.中南大学 交通运输工程学院，湖南 长沙 410075；2.肇庆市交通运输局，广东 肇庆 526060；3.中山大学 智能工程学院，广东 广州 510006)

0 引言

道路交通事故造成的人员伤亡和财产损失是人类社会的主要威胁之一。据世界卫生组织2021年统计，道路交通事故每年大约造成130万人死亡，约2 000万～5 000万人受伤，财产损失约占大部分国家国内生产总值的3%[1]。因此，对道路交通事故进行分析有利于缓解交通安全形势。

交通事故风险预测是交通安全分析的重要分支，也是智能交通系统的重要模块，对降低交通事故发生频率起关键作用。在智能交通管理系统中，一旦知晓某地区在某一时间段事故发生风险较高，可通过信息发布系统提醒驾驶员或自动驾驶车辆绕行，降低事故发生的可能性。在相关文献中，通常采用交通事故发生频率表示特定空间和时间状态下交通事故风险[2]。

交通事故具有典型的时空分布特征[3-4]。交通事故由驾驶员、天气、环境和偶然事件等多种因素造成，事故时空分布数据存在大量噪声，可能掩盖其时空分布特征，所以通过挖掘事故时空分布特征，预测特定时间和空间的事故风险，具有一定挑战性。

国内外学者对交通事故风险预测的研究分为传统统计学类方法和机器学习类方法2类。常用统计学方法包括整合移动平均自回归(ARMIR)模型和向量自回归(VAR)模型。Rabbani等[5]使用单方程自回归方法ARMIR预测中国季度单位时间序列的道路交通死亡人数；Michalaki等[6]建立VAR模型，探讨高速公路碰撞与道路基础设施、社会人口、交通和天气特征之间的动态关系。统计学方法比较适用于分析低维时间序列数据，针对高维交通事故数据处理有一定困难。

部分学者通过机器学习模型，在高维事故数据中学习事故相关因素与事故之间的关系，对事故进行预测。Dong等[7]提出使用支持向量机(SVM)模型解决道路事故预测中高维时空数据处理比较困难的问题。文献[8-9]基于具有时空特征及其他相关特征的事故数据，运用人工神经网络(ANN)和BP神经网络(BPNN)模型预测交通事故。为提高预测模型的准确性，将深度学习模型应用于交通事故预测中：Ren等[2]利用基于长短期记忆神经网络(LSTM)的交通事故风险预测方法，对北京2016年交通事故频率进行预测；Yu等[3]开发深度时空图卷积网络模型(GCN)，捕捉交通事故预测时空模式；Yuan等[4]基于LSTM在挖掘时间特征方面的优势和GCN在挖掘空间特征方面的优势，开发新的卷积长短期记忆神经网络(ConvLSTM)模型。机器和深度学习方法可用于处理高维时空事故数据，但该类方法依赖参数调整，并消耗大量计算资源。因此，开发1种既能高效处理高维数据，又能准确捕获数据中时空相关性的方法十分必要。

动态模态分解(DMD)通过完全数据驱动的无方程策略，可从高维数据中捕捉时空关联性，适合交通事故风险预测系统等缺乏物理特征信息的动态系统。具备无需依赖参数调整、完全数据驱动等优点，被广泛用于流体系统、流行病学系统和金融系统等研究领域[10-12]。

鉴于此，本文基于美国丹佛市2021年7个月的交通事故记录数据，以天为时间单位，以街区为空间单位进行整理，在整理后的数据集上，采用总最小二乘法去除数据噪声，建立结合Hankel矩阵的动态模态分解(Hankel-DMD)模型,进行交通事故风险时空预测，并将预测结果与传统统计分析模型、机器学习模型和传统DMD模型进行对比，验证Hankel-DMD模型的可行性及有效性。

1 Hankel-DMD模型

1.1 动态模态分解

DMD是基于动态系统的分析方法。假设城市交通事故风险波动是1个离散的动态系统，由测量值xt+1和测量值xt组成[13]，如式(1)所示：

xt+1=Axt

(1)

式中：xt是系统在t时的状态，xt∈RN；A是线性算子，A∈RN×N，N是空间维度。构建2个数据矩阵如式(2)～(3)所示：

X=[x1,x2,…,xM-1]

(2)

Y=[x2,x3,…,xM]

(3)

式中：X，Y∈RN×(M-1)，表示动态系统在(1-(M-1))和(2-M)时刻的状态集合，M为时间维度。 DMD最初是针对M≪N的情况进行开发，空间维度可以囊括所有的时空主导模式。结合式(1)～(3)，X，Y之间的关系如式(4)所示：

Y=AX

(4)

找到使X，Y之间的二阶范数规范最小化的最佳线性算子A，即找到A的解，如式(5)所示：

(5)

方程的解可由X的奇异值分解得到，如式(6)所示：

A=YX†=YVΣ-1UT

(6)

式中：†为伪逆运算。

(7)

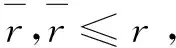
(8)

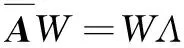
(9)

式中：W包含特征向量；Λ是特征值。

包含动态特性的动态模态Φ由式(10)给出：

(10)

1.2 Hankel-DMD

Hankel-DMD(Dynamic Mode Decomposition with Hankel matrix，Hankel-DMD)为具有Hankel块矩阵的DMD模型。在部分交通事故预测场景中，时间维度总数远远大于空间维度，既N≪M。由于空间维度间存在一定依赖关系，使采用空间模式主导的DMD方法无法囊括所有时空模式，原始DMD公式不足以捕捉系统的全部主要时空特征。为此，将观测值重新排列在Hankel矩阵中，通过将s个时间维度的观测值附加到数据矩阵，以丰富观测值[14]。Hankel矩阵如式(11)～(12)所示：

(11)

(12)

(13)

(14)

(15)

(16)

2 总最小二乘法

总最小二乘法(TLS)是线性最小二乘问题的降噪方法[15]。假设数据D是由理想无噪声数据Dp和噪声E组成，如式(17)所示：

D=Dp+E

(17)

降噪是为了从D中获得Dp的适当估计，总最小二乘法假设无噪声数据Dp与噪声E正交，0为零向量，E为独立同分布，则D的奇异值分解如式(18)所示：

(18)

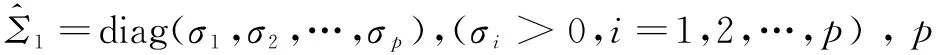
(19)

3 实验分析

3.1 实验数据

本文实验整理了丹佛2021年1月至2021年7月的交通事故记录数据，将数据中的时间和空间信息整合为1个时空矩阵，分别以街区为空间单位，以天为时间单位，整合得到1个交通事故数量分布的时空矩阵，矩阵大小为78×212。

原始数据分布如图1(a)所示，交通事故数据时空分布较离散，为更有效地提取事故时空分布特征，采用总最小二乘法对数据进行降噪，降噪后数据分布如图1(b)所示，噪声明显减少。

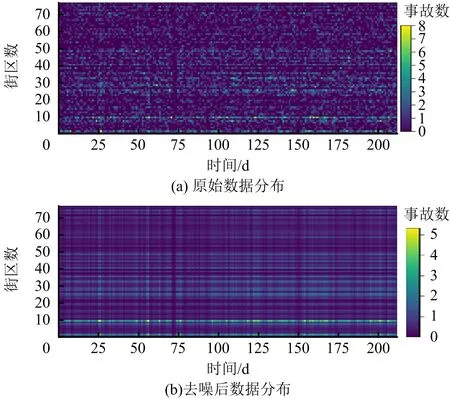
图1 去噪前后实验数据集分布Fig.1 Distribution of experiment data sets before and after denoising

3.2 实验描述

本次实验使用交通事故频率表示某一空间和时间状态下的交通事故风险[2]。为讨论Hankel-DMD交通事故时空风险预测模型性能，将其与统计学方法、机器学习方法和传统的DMD方法预测效果进行比较。

ARMIA是最常用的一类时间序列预测模型，由差分、建模和预测3个步骤组成。ARMIA可以捕捉时间序列数据中变量的演化特征，将演化特征推算到未来，得到预测结果。

支持向量回归机(SVRM)是支持向量机在回归领域的发展，利用非线性映射函数，将输入空间映射到高维特征空间，在特征空间中寻求最优线性函数，以获得原始空间的非线性回归效果。

BPNN是由误差反向传播算法训练的多层前馈网络，通过学习数据中相关因素间的关系进行预测，是使用最广泛的神经网络之一，也是机器学习中最常用的预测方法之一。

LSTM是特殊的递归神经网络，能够学习数据中的长期依赖关系，该模型的递归模块由多个层相互作用地组合，常用于时间序列预测。

ConvLSTM是有卷积结构的递归神经网络，将能够抽取空间特征的卷积操作增加至能抽时序特征的LSTM网络中，常用于时空预测。

在数据集中，选取前160个时刻数据作为训练数据，后52个时刻数据作为测试数据。同时，分别评估模型的单步预测和多步预测准确性，单步预测为预测1 d，最大预测长度为7 d，使用平均绝对误差(MAE)和均方根误差(RMSE)对预测结果进行评估。MAE代表数据集中实际值和预测值之间绝对差异的平均值，衡量数据集中残差的平均值，反映预测误差的实际情况。定义Pt和Ot分别表示预测值和观测值[16]，MAE计算如式(20)所示：

(20)

RMSE用来衡量残差的标准偏差，评估数据的变化程度[16]，RMSE计算如式(21)所示：

(21)

3.3 结果分析

1)模型结果比较分析

Hankel-DMD模型和其他模型的交通事故预测性能对比见表1，当MAE，RMSE越小，表示预测模型准确性越好。由表1可知，Hankel-DMD模型在本文实验中整体预测效果相对最佳，DMD模型表现仅次于Hankel-DMD模型；随预测步数增加，所有模型MAE，RMSE逐渐增加，但DMD和Hankel-DMD的增长趋势相对较小，这说明DMD系列模型除单步预测精度较高外，多步预测的误差增长率低于其他方法。上述结果验证DMD系列模型在交通事故风险的时空预测方面的有效性和高准确性。

表1 不同模型方法对不同预测步长任务性能的比较Table 1 Comparison of performance for tasks with different prediction steps by different model methods

2) Hankel-DMD结果分析

测试集数据及DMD重构数据分布如图2所示，DMD重构数据捕获事故频发的关键街区(如第1，9街区)和关键时间(如第42，47 d)。

图2 测试数据和DMD重构数据的时空分布比较Fig.2 Comparison of spatio-temporal distribution of test data and DMD reconstructed data

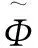
图3 Hankel-DMD提取的动态模态和特征值Fig.3 Dynamic modes and eigenvalues extracted by Hankel-DMD

Hankel-DMD模型提取的10个特征值如图3(b)所示。特征值表示动态模态的时间演化特性：如果特征值虚部为0，那么相应动态模态存在振荡特性；如果特征值在单位圆内，动态模态存在衰减特性；如果特征值在单位圆外，动态模态有增长特性[18]。由3(b)可知，特征值点在单位圆内或单位圆上，其中，有9个特征值在单位圆内，1个特征值在单位圆上，其虚部为0。由此可知，交通事故风险预测Hankel-DMD模型主要动态模态的时间演化特性分为振荡和衰减2种。这说明特征值捕捉到丹佛交通事故动态系统的主要时间演化特征为一定周期性和逐渐下降的特点。

综上，Hankel-DMD中的动态模态和特征值可捕捉城市交通事故风险发生的时空关联性，同时，可以利用低秩解从高维交通事故数据中探索时空相关性，在交通事故风险时空预测任务中表现较好。因此，Hankel-DMD模型比较适用于城市交通事故的时空数据分析任务。

4 结论

1)提出使用总最小二乘法去除事故数据噪声，并建立结合Hankel矩阵的动态模态分解模型(Hankel-DMD)，用于交通事故风险的时空预测;Hankel-DMD模型可基于具有一定数据噪声的高维交通事故数据,捕捉事故的时空一致性关系，并预测交通事故风险。

2)应用统计学、机器学习、深度学习及传统动态模态分解方法，与Hankel-DMD模型进行比较，结果显示Hankel-DMD模型在MAE，RMSE方面的表现较优。

3)Hankel-DMD预测过程中产生的动态模态,可解释城市交通事故风险预测动态系统的空间特性，进而解释系统的时间特性。Hankel-DMD模型的结果具有一定的可解释性，适用于城市交通事故风险时空预测。