基于基本顶断裂位置分析剩余煤柱稳定性*

王志强，田 野，王树帅，牟皓奇，刘吟苍

(1.中国矿业大学(北京) 能源与矿业学院，北京 100083；2.中国矿业大学(北京) 力学与建筑工程学院，北京 100083)

0 引言

综采工作面支架回撤是矿井生产的重要环节，无预掘回撤通道、预掘单回撤通道和预掘双回撤通道是应用最广泛的支架回撤工艺[1]。工作面在向回撤通道推进的过程中，工作面与回撤通道间煤体宽度不断减小，最终转变为1条“窄煤柱”。煤柱稳定性对保障工作面安全及回撤通道的稳定具有重要影响，若对煤柱的稳定性掌握不足，容易引发煤柱脆性破坏、回撤通道垮塌、支架压架等事故[2]。

目前，分析剩余煤柱稳定性主要有理论分析、数值模拟和现场实测3种方法。在理论分析中，大多采用极限平衡区公式求解煤柱极限宽度，认为煤柱两侧支承应力峰值叠加区宽度，即为煤柱极限宽度。侯朝炯等[3]、李树清等[4]、于远祥等[5]分别采用极限平衡理论、弹塑性极限平衡理论及弹性理论对极限平衡区的煤柱稳定性进行分析，推导出极限平衡区宽度；除极限平衡区外，谷拴成等[6]、王志强等[7]利用极限平衡区公式和压力拱模型共同确定贯通前煤柱上方载荷及煤柱极限宽度；谷拴成等[8]建立贯通前剩余煤柱两侧的载荷力学模型，将回撤通道两侧煤壁和工作面前方煤壁均视为固支端，求解出剩余煤柱载荷及宽度。数值模拟也是分析煤柱稳定性的有效方法，其可以系统地计算出不同煤柱宽度下巷道围岩的变形、塑性区及应力分布情况[9-10]。现场实测[11]是确定煤柱载荷和确定极限宽度重要手段之一，且具有高精确性、现场实用性，但需要在现场进行实时观测，所以工程比较复杂。

本文以工作面与回撤通道之间的剩余煤柱为研究对象，基于贯通前基本顶断裂位置，简化煤柱上方支承应力表达式，建立剩余煤柱载荷力学模型，计算剩余煤柱载荷及煤柱极限宽度，并分析地质因素与工程因素对剩余煤柱稳定性的影响规律。简化后的支承应力表达式可更加精确地计算煤柱所承受载荷，同时可更加全面地分析各因素对剩余煤柱稳定性的影响规律。

1 工程概况

梧桐庄2号煤层三采区182312走向工作面(简称312工作面)是三采区最后1个走向工作面。梧桐庄2号煤层平均厚度3.4 m，平均倾角11°。埋深约为500 m。312工作面布置如图1所示。312工作面利用三采右翼出煤巷(简称出煤巷)作为支架的回撤通道[12-13]。

图1 182312工作面布置Fig.1 Layout of 182312 working face

工作面在贯通前，根据基本顶断裂位置与出煤巷的位置关系，基本顶最后1次断裂主要有如图2所示的3种形式[14-15]：①在出煤巷左侧实体煤上方断裂；②在出煤巷上方断裂；③在剩余煤柱上方断裂。

图2 基本顶不同断裂形式示意Fig.2 Schematic diagram of different fracture forms of basic roof

图2中，lz为基本顶周期断裂步距，d为基本顶断裂位置距离出煤巷非开采帮煤体破碎区边缘的距离。由基本顶周期断裂步距(17.9～20.8 m)得，312工作面基本顶最后1次实际断裂位置位于剩余煤柱上方，d取值范围为8.6～11.5 m。若lz取平均断裂步距20 m，则d约为10.7 m。(注：本文理论计算过程中，lz取20 m，d取10.7 m，而后分析d=8.6～11.5 m时煤柱宽度范围值。)

2 剩余煤柱稳定性分析

2.1 剩余煤柱载荷力学模型建立

312工作面在贯通前，基本顶在剩余煤柱上方断裂。因此，建立基本顶此种断裂形式下剩余煤柱载荷力学模型，分析剩余煤柱载荷及极限宽度。基本顶在来压时对煤柱的载荷最大，也即假设基本顶在预断裂位置处于来压断裂状态，此时煤柱所受载荷最大，此种情况下所求得的极限宽度更具有一定的安全系数。本文在文献[8]模型的基础上，考虑关键块B整体对煤柱的载荷，不仅考虑支架上方的控顶部分，同时考虑支架后方作用在矸石的简支部分，使煤柱承受的载荷更加全面。本文建立的载荷力学模型如图3所示。

图3 煤柱载荷力学模型Fig.3 Mechanical model of coal pillars load

图3中，以出煤巷非开采帮煤体破碎区边缘为x轴原点O，基本顶在断裂处左端为支承应力峰值位置，此处的应力为kγH，MPa，其中，k为应力集中系数，γ为岩石容重，MPa/m，H为煤层埋藏深度，m；q(x)为支承压力，MPa；qm为关键块B跨落后的重力，MPa；f1为出煤巷巷内支柱支护阻力，MPa；f2为支架工作阻力，MPa；B0为剩余煤柱承载宽度，m；R1为煤体(柱)破碎区宽度，m；D1为出煤巷跨度，m；D2为支架控顶距，m。

2.2 剩余煤柱载荷分析

在分析煤柱受力时，将煤柱从基本顶断裂位置划分为左、右2部分，在基本顶断裂位置左侧，力学模型如图4所示。

图4 基本顶断裂位置左侧载荷分析Fig.4 Load analysis on left side of fracture location of basic roof

由文献[10]知支承应力q(x)如式(1)所示：

(1)

式中：q(x)为支承应力，MPa；f为煤层内摩擦力，MPa；M为工作面采高，m；β为侧压力系数。

由式(1)可以看出q(x)函数形式比较复杂，不易对其进行积分及确定重心。本文将其简化为图4所示的关于x的n(n取整数)阶幂指数函数，即把应力曲线拟合为关于x的n次抛物线[16]。当d及n取不同值时，关于x的n阶函数通式(x=0,1,2,…,d)如式(2)～(4)所示：

q(xn)=q1+λn(d-x)n

(2)

其中：

(3)

(4)

在分析煤柱上方载荷时，将支承应力q(x)简化为均匀载荷q1和从0连续递增到q2的n次抛物线形载荷。图4中A，l，h分别表示抛物线的面积、长度和高度。F1，F21分别为出煤巷左侧实体煤和剩余煤柱对顶板的支撑力，由力的相互作用，得2力为上覆岩层对出煤巷两侧煤体的载荷。q2表达式及q1，q2，f1对顶板的作用力分别如式(5)～(8)所示：

(5)

(6)

(7)

Qf1=f1D1

(8)

在断裂位置左侧，在基本顶断裂处为简支。图4模型右侧弯矩为0，即如式(9)所示：

(9)

由式(9)得F1如式(10)所示：

(10)

由y方向的力平衡得F21如式(11)所示：

(11)

基本顶断裂位置右侧，力学模型如图5所示。

图5 基本顶断裂位置右侧载荷分析Fig.5 Load analysis on right side of fracture location of basic roof

图5中：F22，F3分别为煤柱和采空区垮落矸石对顶板的支撑力。该模型两端均为简支，同样的，右侧简支处弯矩为0，即如式(12)所示：

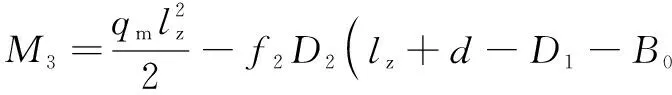
(12)

其中R1的表达如式(13)[16-17]所示：

(13)

式中：φ为煤层内摩擦角，(°)；h为煤层厚度，m；C为煤体黏聚力，MPa。

由式(12)～(13)得F22，如式(14)所示：

(14)

综合基本顶断裂位置两侧的力学模型，结合式(11)及(14)，可得煤柱对顶板的总支撑力F2，如式(15)所示：

(15)

因此，由力的相互作用得剩余煤柱受力为F2。则工作面与上山间的剩余煤柱平均应力如式(16)所示：

(16)

2.3 剩余煤柱极限宽度计算

煤柱的极限强度可参考比涅乌斯基(Bieniaski)煤柱强度计算公式(17)[15]：

(17)

式中：σp为煤柱极限强度，MPa；σc为煤柱单轴抗压强度，MPa；M为工作面采高，m。

当煤柱平均应力σa达到极限强度σp时(见式(18))，煤柱处于极限平衡状态。

(18)

将式(15)～(17)带入式(18)，可得煤柱承载宽度B0，如式(19)所示：

(19)

其中，a,b,c计算如式(20)所示：

(20)

因此，煤柱极限宽度B，如式(21)所示：

B=B0+2R1

(21)

由煤柱宽度表达式(21)可以看出，影响煤柱宽度的因素可分为地质因素和工程因素，312工作面各因素参数及数值见表1。

表1 312工作面地质与工程参数Table 1 Geological and engineering parameters of 312 working face

本文的力学模型基于基本顶断裂位置建立。支承应力q(x)曲线所对应的x的抛物线的次数n随着断裂位置d不同而发生变化。取d=7～15 m，经拟合后发现：当d=7，8，9 m时，n=3；当d=10，11，12 m时，n=4；当d=13，14 m时，n=5；当d=15 m 时，n=6。限于篇幅，结合d=10.7 m时，绘制d=10，11 m时的原函数与n次抛物线的拟合曲线对比图，如图6所示。

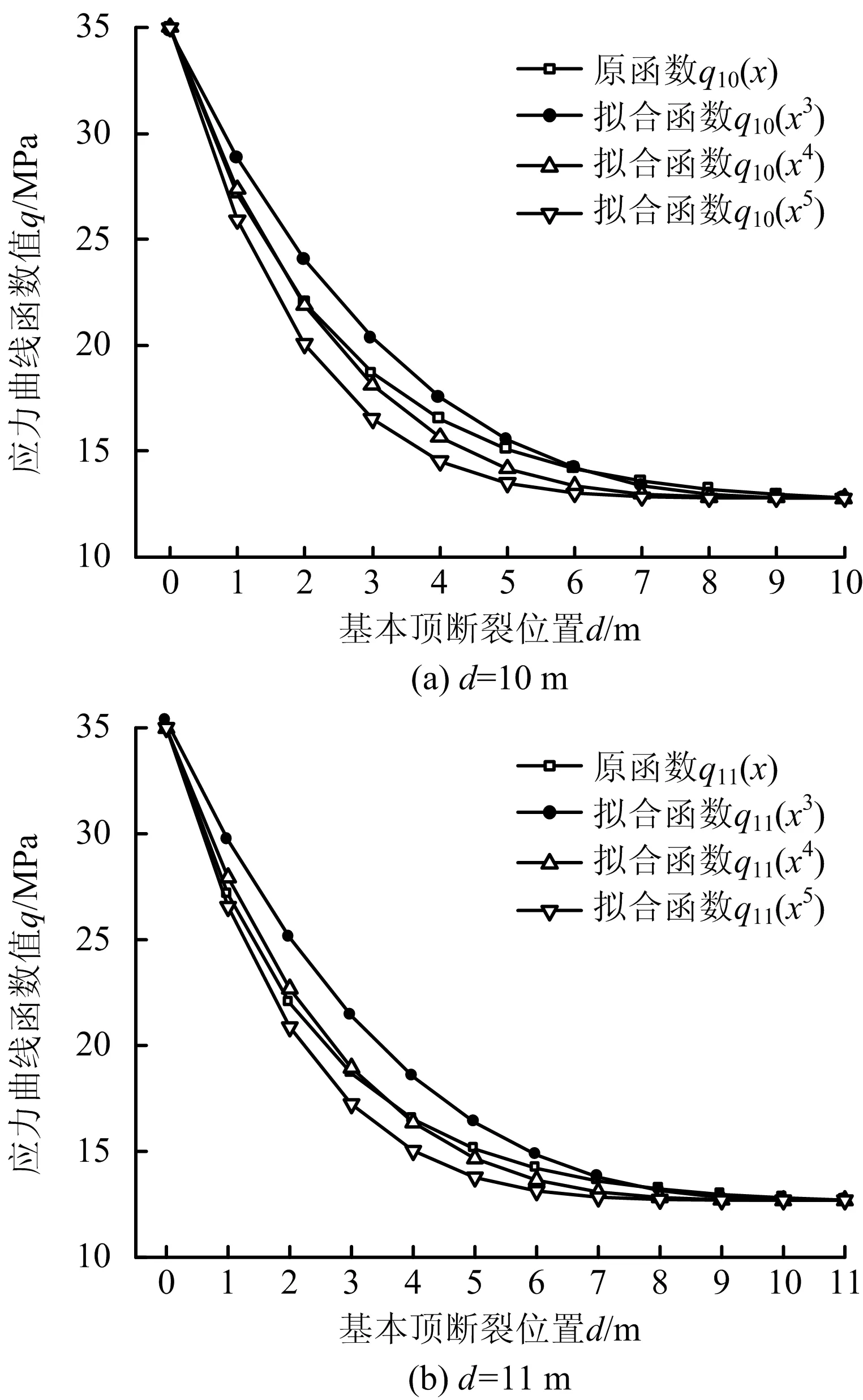
图6 应力曲线与抛物线拟合情况Fig.6 Stress curves and parabolic fitting

由图6知当d=10，11 m时，n都为4，其中q10(x4)=12.802+2.25×10-3(10-x)4；q11(x4)=12.697+1.54×10-3(11-x)4。因此，当d=10.7 m时，n也取4，也即与支承应力q(x)拟合效果最好的为4次抛物线。此时，由表1参数及式(19)计算得煤柱承载极限宽度B0约为6.05 m，由式(13)计算煤柱破碎区宽度R1为1.26 m，因此，煤柱极限宽度B为8.57 m。

注：同理，当d=8.6 m时，n=3，由公式计算得B=8.06 m；当d=11.5 m时，n=4，此时B=8.85 m。因此，当基本顶最后一次断裂步距lz为17.9～20.8 m时，也即当d取8.6～11.5 m时，剩余煤柱极限宽度B的取值范围为8.06～8.85 m。

3 剩余煤柱稳定性影响因素分析

本文力学模型是基于基本顶断裂位置建立的，首先分析基本顶断裂位置d对剩余煤柱极限宽度与平均应力的影响，进而结合剩余煤柱极限宽度B的表达式及表1各因素，分析各地质因素与工程因素对剩余煤柱极限宽度的影响规律。

3.1 基本顶断裂位置影响规律分析

基本顶断裂位置d对剩余煤柱稳定性的影响规律如图7所示。

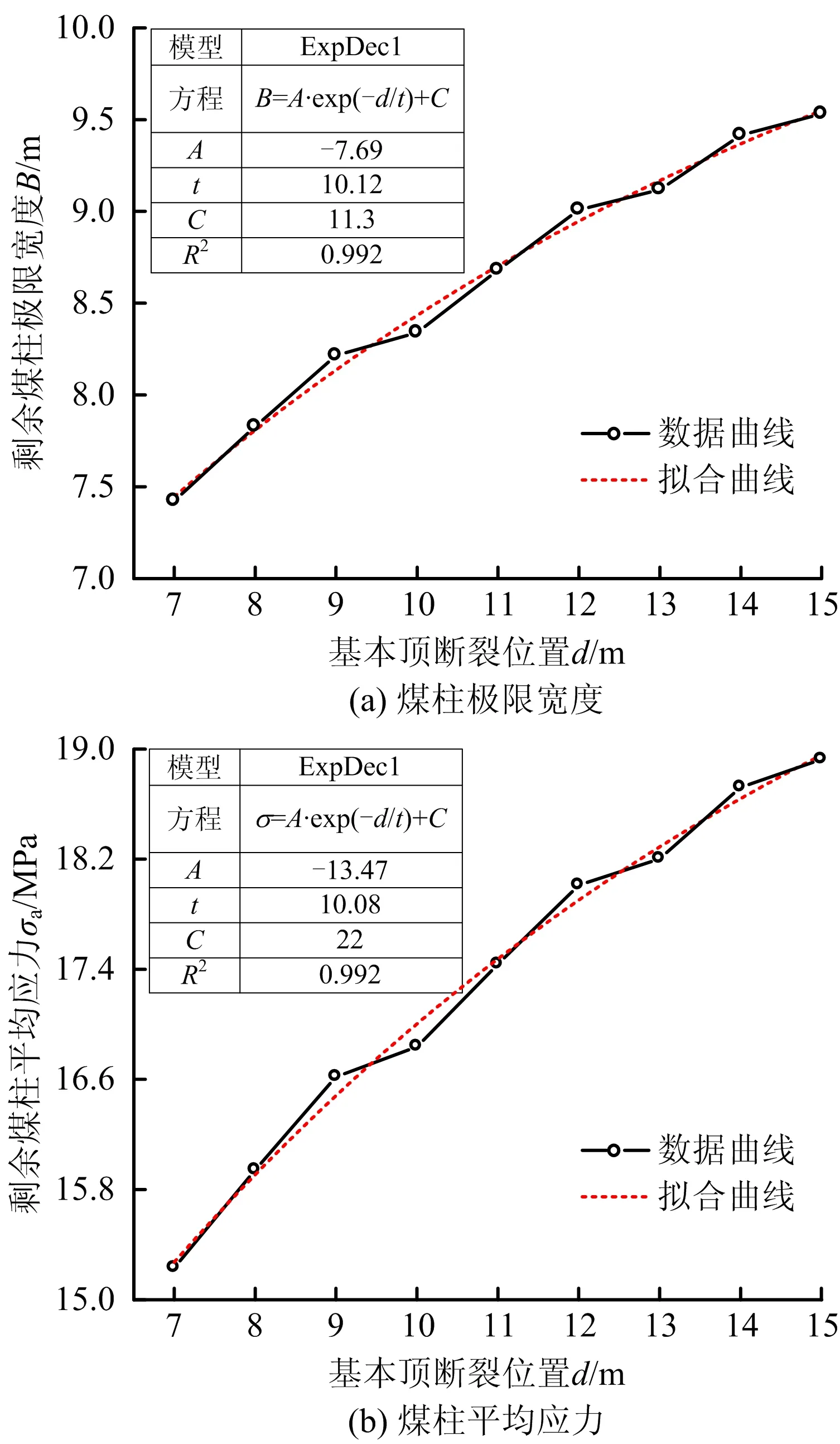
图7 基本顶断裂位置d对煤柱稳定性的影响Fig.7 Influence of fracture position of basic roof d on stability of coal pillars

利用单相指数衰减函数对数据曲线进行拟合，剩余煤柱极限宽度拟合函数表达式：B=-7.69×e-x/10.12+11.30，其中R12=0.992。剩余煤柱平均应力拟合函数表达式：σ=-13.47×e-x/10.08+22.00，其中R22=0.991。由图7可看出：随着d增大，即随着直接顶断裂位置远离上山，剩余煤柱极限宽度B和平均应力σa也随之增加，d在7～15 m区间内，极限宽度B由7.42 m增加到9.53 m，平均应力σa由15.23 MPa增加到18.92 MPa，但二者的增加幅度均逐渐变小。由上述分析可以看出，随着基本顶断裂位置远离上山，剩余煤柱平均应力逐渐增加，表明其稳定性逐渐降低，相应的所需极限宽度有所增大。

图8～9分别分析了表1中各地质因素和工程因素对剩余煤柱极限宽度的影响规律，各图中，实线表示剩余煤柱极限宽度，虚线表示单位变化量。

3.2 地质因素影响规律分析

由图8(a)～(h)可知，在本文中影响煤柱极限宽度的8种地质因素中，煤层黏聚力C、侧压力系数β、煤层内摩擦角φ、煤层埋深H、煤层厚度h、应力集中系数k对煤柱极限宽度影响显著，影响程度分别为-7.47 m(-59.56%)，7.17 m(105.4%)，-5.18 m(-44.33%)，3.46 m(50.06%)，2.98 m(39.61%)，1.87 m(23.64%)。其中煤层黏聚力C和侧压力系数β影响最为显著。采空区垮落岩层重力qm及基本顶周期破断距lz对煤柱极限宽度影响效果较小，煤柱极限宽度的变化量均在0.5 m以内。

图8 地质因素对煤柱极限宽度的影响规律Fig.8 Influence of geological factors on limit width of coal pillars

其中，煤层黏聚力C及煤层内摩擦角φ的影响规律相似，随着两者的增大，煤柱极限宽度都减小；而两者变化的不同为：煤层黏聚力C的单位变化量影响曲线为光滑曲线，而煤层内摩擦角φ的影响曲线有明显的拐点；煤层埋深H和应力集中系数k的影响规律相似，随着两者的增大，煤柱极限宽度都增加，但单位变化量均呈逐渐减小的趋势；侧压力系数β与煤层厚度h的影响规律相似，随着两者的增大，煤柱极限宽度都增加，侧压力系数β的单位变化量虽有一定的变化，但是煤柱极限宽度几乎呈直线增加，与煤层厚度h影响规律相似。

3.3 工程因素影响规律分析

由图9(a)～(e)可知，在本文中影响煤柱极限宽度的5种工程因素中，只有工作面采高M的影响效果显著，随着M的增加，煤柱极限宽度逐渐增加，增加了2.66 m(35.18%)，而单位变化量呈逐渐减小的趋势。其余4种因素对煤柱极限宽度无明显影响，煤柱极限宽度及单位变化量的影响曲线都近似为一条水平直线。

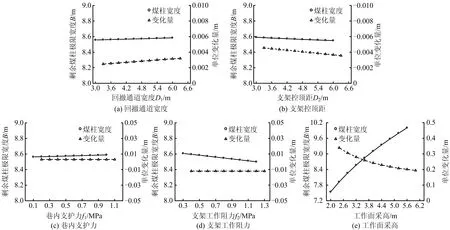
图9 工程因素对煤柱极限宽度的影响规律Fig.9 Influence of engineering factors on limit width of coal pillars

结合图8～9，地质因素较工程因素对煤柱极限宽度的影响更加显著，即地质因素是决定煤柱极限宽度的根本因素。但地质因素往往是固有参数，结合工作面采高对煤柱极限宽度的影响规律，在实际生产过程中，可通过调节工作面采高来控制煤柱极限宽度，提高煤柱的稳定性。

4 结论

1)基于基本顶断裂位置建立工作面与回撤通道间煤柱载荷力学模型，考虑支承应力q(x)和关键块B整体作用力qm，并将支承应力q(x)简化为关于幂函数抛物线q(xn)，计算得煤柱极限宽度范围为8.06～8.85 m。

2)随着基本顶断裂位置d远离上山，剩余煤柱载荷与极限宽度均增大，但二者的增大幅度均呈下降趋势。

3)分析剩余煤柱极限宽度随影响因素的变化规律：煤层黏聚力C、内摩擦角φ、侧压力系数β、煤层厚度h、煤层埋深H、应力集中系数k及工作面采高M的影响效果显著，其余因素影响效果甚微。