模糊数学算法在高职院校产教融合评价中的应用研究

王聪

(长沙职业技术学院，湖南长沙 410217)

1 问题的提出

产教融合：是指职业学校根据所设专业，积极开办专业产业，把产业与教学密切结合，相互支持，相互促进，把学校办成集人才培养，科学研究，科技服务为一体的产业性经营实体，形成学校与企业浑然一体的办学模式。有利于激发学生的创造力、创新力，并为学生工读结合、勤工俭学创造条件。积极推进产教融合、校企合作，努力推进“校中厂、厂中校”，真正实现“教、学、做”合一，其意义：一是能够有利于提高教师的业务水平。通过实际操作，不断提升教师的动手能力和知识应用能力，从而不断提升教学质量。二是有利于促进地方经济的发展。通过与企业合作的方式，能培养一大批懂技术、会管理的人才，解决企业急需的人才困境。三是有利于促进职业教育健康发展。职业教育是以就业为导向的教育，“产教结合，校企一体”的培养思路正是这种需求的集中体现。故在《提质培优行动计划》中反复提及。

而目前国内研究的现状是，较多的研究者聚焦于对产教融合评价指标体系的研究，例如，吴结(2011) 认为应从“合作办学、合作育人、合作就业、合作创新、合作发展[1]”等5 个维度评价高职教育校企深度合作模式……王霞(2014)分析了高新区产城融合的影响因素，建立了高新区产城融合度评价指标体系[2]，并进行了实证；而对于高职院校“校企融合度”的定量评价研究关注较少，本文尝试运用模糊数学算法，来对校企融合度进行定量分析评价，从而为其他兄弟院校提供借鉴。

2 数学模型

根据学校产教融合度评价指标体系，由合作企业基本情况、教育教学、实习实训、就业服务、学生满意等五个一级指标组成，故设定产教融合度的评价因素为5 个，由此构成评价因素集X={x1,x2…xm}。对于产教融合度的总体评价而言，每个评价因素又包括相应的等级，例如：优秀、良好、较好、中、差。故评价等级决策集可表示为：Y={y1,y2…yn}。用i 和j 分别来表示具体的评价因素和评价水平等级，从而构建各指标与评价等级子集所构成的模糊关系矩阵R，如下所示。

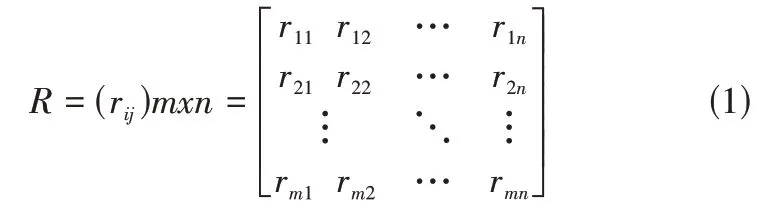
上式中，rij表示指标xi所描述的性质隶属于评价等级决策集yj所表示的评价等级的程度，且=1。从而构建出模糊关系矩阵R，并可分别着眼单个评估指标与评价等级决策集之间的关系，求解其模糊隶属度向量。

由于评价因素的权重不同，我们可以用K来表示X评价因素集权重分配，且K={k1,k2…kn}。因此，xi的数量指标由ki来表示，根据A=k·R 计算获取各种决策的可能性系数，具体由A=(a1，a2…an)表示，然后根据最大隶属度原则，选出最大的aj，其所对应的yj表示评价结果，具体表达式如下。

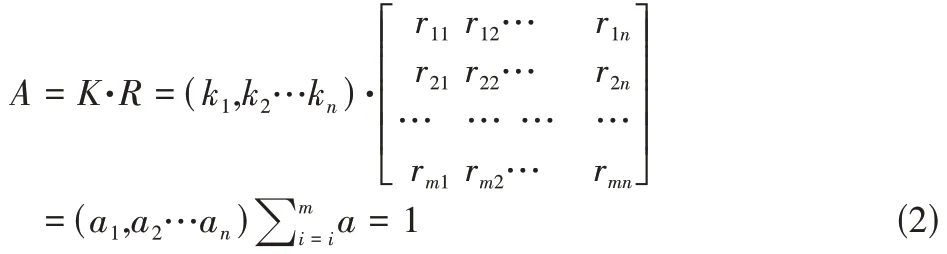
对结果A采用总和归一化(sumNormalizer)来进行处理，即：

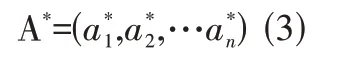
其中：

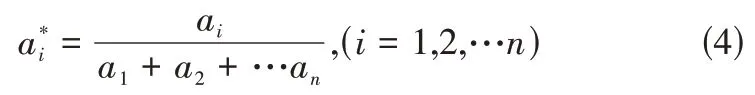
A*是归一化后的评价结果，为了能得到综合评价，再把各等级的权重与A*的数值进行整合，从而得到最终结果。

设等级Vi的权重所组成的向量为

综合评价结果的计算为：

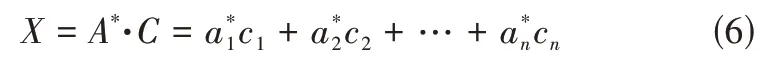
以上就是使用模糊数学算法来计算产教融合度的过程，接下来，将以实际的案例来进行说明。

3 应用实例

学校制定了《校企合作管理办法》，建立校企合作企业库，采取动态调整机制，优化校企合作企业，不断加大合作密切型企业占比。为此，需要针对与企业的合作程度、效果、学生满意度等多个维度来进行评判，得出结论供决策使用。因此，尝试使用模糊数学算法来得出产教融合度。

3.1 校企合作评价指标体系

首先，需要构建一个科学合理的指标体系，来评价校企合作企业，为评价结果提供必要的可靠性和认可度。其次，评价项目应该全面、有针对性、可操作性高的评价项目(因素)构成，而相关的权重应能将评价项目有机地联系起来[3]。因此，评价体系主要包括了评价因素和权重。

3.1.1 评价因素和权重

根据学校《校企合作管理办法》，关于产教融合度的评价因素，基于制定的校企合作管理办法[4]，由五个方面构成，分别是：合作企业基本情况、教育教学、实习实训、就业服务、学生满意度，其权重和分值见下表1。

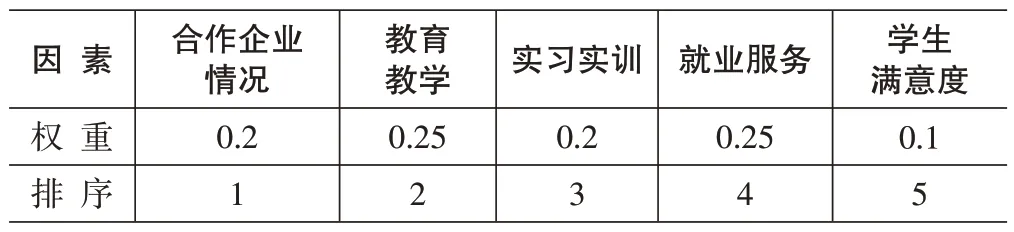
表1 影响因素、权重及排序

由上表可知，影响因素集中X={x1,x2,x3,x4,x5},而每个因素对于产教融合度评价的权重集则为A=(0.2,0.25,0.2,0.25,0.15)。

3.1.2 确定产教融合度评价集

根据学校《校企合作管理办法》中的要求，对合作企业的评价等级分为五级，具体的评价集为：

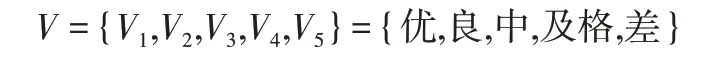
换算为百分制来表示，优对应90分以上；良对应80～89分；中对应70～79分；及格对应60～69分；差对应59分以下，在本案例中，计算时选取各等级的中值分，即：优(95)、良(85)、中(75)、及格(65)、差(55)。

3.1.3 评价人员构成及权重

对校企合作企业的评价人员由学校、学生、二级学院组成，利用特尔斐法，确定权重分别为学校(0.5)、学生(0.3)、二级学院(0.2)。随机选取一份校企合作企业评价的数据表，如表2。

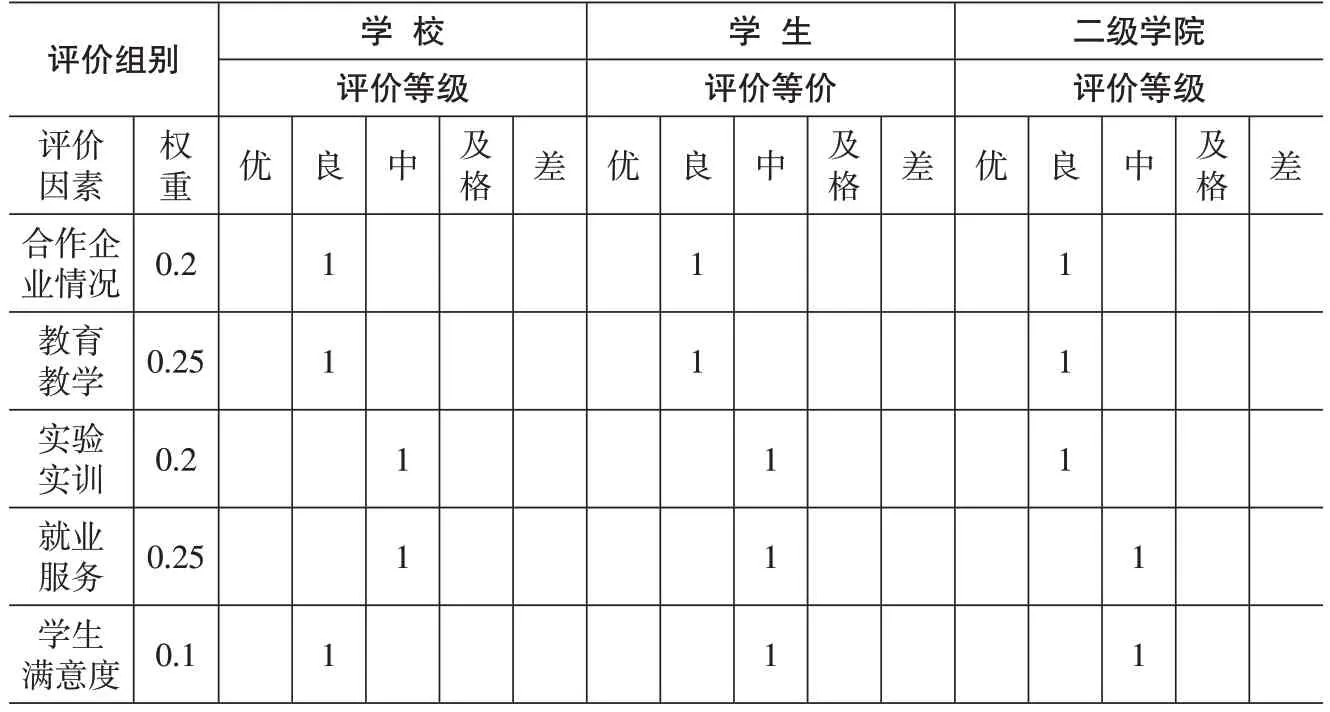
表2 校企合作企业评价表

3.2 评价矩阵

随机选取一份学校对校企合作企业的评价表(见表2)，使用上表2中的数据，我们可以尝试来构建对校企合作企业的评价矩阵。矩阵的每一行，对应评价因素，每一列对应评价等级，其对应值为“评价人员”评价等级加权。以“合作企业情况”因素为例，其在“学校”“学生”“二级学院”的评价中均为“良”，按照评价人员权重来进行计算得到0.5*1+0.3*1+0.2*1=1，故矩阵第一行对应“良”列其值为“1”。再如，“实验实训”，其评价对象既有“中”，又有“良”，其计算依据为，“良”列值为0.2*1=0.2，“中”列值为0.5*1+0.3*1=0.8，故矩阵第三行值为“0,0.2，0.8,0,0”。具体计算后的矩阵如公式7所示。

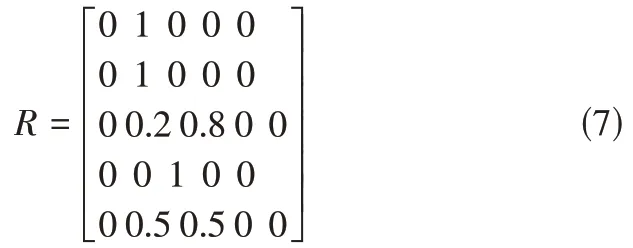
3.3 综合评价运算

从上表2 中的评价因素，我们可以得到“合作企业情况”“教育教学”、“实验实训”、“就业服务”的权重分别为“0.2”“0.25”“0.2”“0.25”“0.1”，故K=(0.2 0.25 0.2 0.25 0.1)。矩阵R可有公式7 得到，使用A=K·R 计算出各种决策的可能性系数，具体计算结果如下所示。

通过上面的计算，我们就得出了各种决策的可能性系数。

3.4 数据归一化处理

在此基础上，对上面运算出的结果进行归一化处理。其原因在于不同评价指标往往具有不同的量纲和量纲单位，而这会影响到数据分析的结果。故为了能消除评价指标之间的量纲所造成的影响，就需要对数据进行标准化处理，使得处理后的数据在同一数量级，从而便于综合对比评价。根据公式8所计算的结果，我们来做归一化处理，A'中各项的分母为0+0.44+0.46+0+0=0.9，具体计算如下：

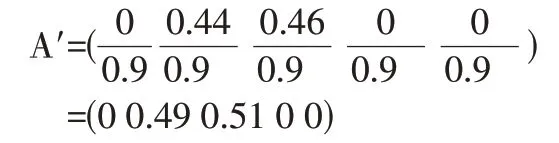
3.5 综合评价运算

在前面我们设置评价等级权重“优、良、中、及格、差”分别取值为“95、85、75、65、55”，故可以得到等级分数矩阵为：C=(95 85 75 65 55)T，这样，我们就可以通过公式X=A*·C[5]来计算出校企合作企业的综合评价值，具体计算如下：

通过上述计算，得到该校企合作企业的综合评价值为79.9，达到评价“中”等次。以上是以学校为实例，用模糊数学算法计算产教融合度的全过程。

4 结论

本文所介绍的方法，是尝试将模糊数学算法应用到校企合作产教融合度的评价上，从评价指标构建、建立评价集合,构建模糊评价矩阵,结合评估指标体系中的各项权重得到评价结果，以规避在评测过程中出现的不确定性问题，为产教融合评价提供新思路、新方法、新途径。