多效率扰动下复杂热力系统能效分析与评价方法
陈海平, 薛凯丽, 张 衡
(华北电力大学 能源动力与机械工程学院, 北京 102206)
火力发电厂是能源消耗大户,是复杂热力系统的应用典范。实现复杂热力系统的集成与优化,既是提高火力发电厂经济效益的有效途径,也是实现国家“双碳目标[1]”的重要一环。因此,如何评价复杂热力系统在多效率扰动模式下的能效水平,考察不同边界条件下总系统的能耗分布及其影响权重,是一个亟待解决的关键问题。
对于1个由多个子系统或热力设备构成的发电厂热力系统(综合系统),其总效率等于各分效率的连乘。众所周知,机组实际运行过程中,综合系统的效率扰动源可能是单一的,但多数情景下是多种效率扰动源同时存在的,即多个子系统或热力设备的效率是同时改变和相互耦合的。值得注意的是,即使仅有单一扰动源,也可能引起多个热力设备的效率发生变化。目前,关于多效率扰动源模式下综合系统的能效分析与评价方法却鲜有报道,相关研究主要集中在子系统或某些热力设备运行能效和评价方法上,属于局部优化的范畴[2]。杨勇平等[3]针对蒸汽朗肯循环和S-CO2布雷顿循环的典型流程,提出了一种热力循环流程重构能效分析方法。张春发等[4]针对火电机组热力系统的构成特点,从不同视角考察了主要运行参数和辅助汽水流量等因素对机组热力系统运行热经济性的影响。闫顺林[5]探究了多元扰动下汽轮机汽水动力循环运行能耗的时空分布及其耦合机制,获得机组在多元扰动下的能效指标变化幅度及其分布规律。周少祥等[6]针对火电机组构建了系统总熵产计算模型,并导出了超超临界机组锅炉烟气余热回收用于加热凝结水的节约能量计算公式。Usn等[7]研究了热力系统中效率较低部分的位置和量级,建立了系统中某一设备的损失和效率的分析计算模型。慈文斌等[8]提出一种多时间尺度电热综合能源系统状态估计方法。刘刚[9]以锅炉及其辅助系统为对象,研究了影响能效指标的底层因素,建立了基于神经网络软测量模型和主元分析的诊断模型。张春发等[10]综合考虑煤质挥发分、灰分、水分变化及运行工况变化对锅炉效率的影响,导出了锅炉机械不完全燃烧损失q4的解析评估模型。孙浩祖等[11]研究了机组变工况运行时管道热效率对机组运行能效的影响。刘磊[12]针对管道效率计算过程中存在的问题,改进了反平衡管道效率的计算方法,明确了管道效率对综合系统节能潜力的影响规律。
上述研究均表明,子系统效率的改善且单独作用于综合系统均有利于综合系统热经济性的提高。但是,实际系统运行过程中,由于子系统及其热力设备对综合系统运行性能产生的影响属于多效率扰动源同时作用,实际运行值与仅考虑单效率扰动影响的计算值存在一定的偏差,综合系统的运行性能并非最优。
为此,在总结单效率扰动模式下电厂热力系统节能分析计算方法的基础上,系统研究多效率扰动模式对综合系统运行性能的影响机制,提出多个子系统或热力设备的热效率同时变化时综合系统运行热经济性的能效分析与评价方法,以期为复杂热力系统节能分析与能效评价提供理论支撑,为综合系统的节能增效工作提供指导。
1 能效评价指标及其计算方法
图1为典型火电厂原则性热力系统,该系统是由锅炉热力系统、汽轮机热力系统、管道系统、联轴器及发电机电气系统组成的一个复杂发电系统。
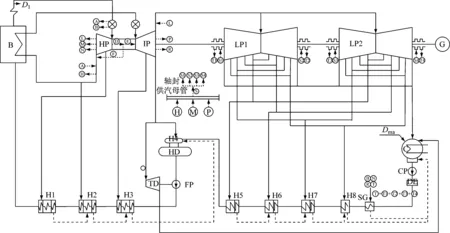
D1—全厂汽水损失; Dma—锅炉补水量; HP—高压缸; IP—中压缸; LP1—低压缸1; LP2—低压缸2; TD—小汽轮机; FP—给水泵;HD—除氧器; SG—轴封加热器; DE—凝结水精处理器; CP—凝结水泵; H1~H3, H5~H8均为回热加热器。
1.1 能效评价指标
火电厂运行能效评价指标中,供电标准煤耗率是发电厂各方面工作水平的反映,是火力发电系统运行热经济性能评价的总指标。与供电标准煤耗率紧密关联的二级评价指标主要有发电标准煤耗率、全厂热效率和热耗率。其计算表达式分别为:
(1)
(2)
(3)
(4)
式中:bcp,n为供电标准煤耗率,kg/(kW·h);ξap为厂用电率,%;bcp,s为发电标准煤耗率,kg/(kW·h);ηcp、ηb、ηp、ηi、ηm、ηg分别为全厂热效率、锅炉热效率、管道热效率、汽轮机循环热效率、机械效率和发电机效率,%;qcp为热耗率,kJ/(kW·h)。
由式(2)~式(4)可知,qcp、bcp,s、ηcp三者知其一,即可求得其余2项,进而可求得其他能效评价指标。在工程应用中,一般情况下计算全厂热效率较为方便。
1.2 能效评价指标的变化及其关系
进行电厂运行能效分析时,一般用能效指标的绝对变化量或相对变化率来表征其变化程度,表1给出了全厂热效率、热耗率和发电标准煤耗率变化值的计算公式[13],其中带“ ′”者表示变化后的参数。

表1 能效指标的变化Tab.1 Changes in energy efficiency indicators
当采用发电标准煤耗率和热耗率指标的相对变化率来表征电厂运行能效变化时,其相对变化率的绝对值是相同的[14],即
(5)
式中:δqcp和δbcp,s分别为qcp和bcp,s以变化前为基准的相对变化率。
工程应用中,全厂热效率相对变化率的计算较为方便,故系统运行能效分析计算的主要任务就是导出全厂热效率相对变化率δηcp的分析计算模型。据此,可求出电厂其他能效评价指标绝对变化量的计算公式。
发电标准煤耗率绝对变化量Δbcp,s:
(6)
年耗发电标准煤绝对变化量ΔBcp,s:
(7)
式中:Bcp,s为年耗发电标准煤,kg。
热耗率绝对变化量Δqcp:
(8)
2 单效率扰动下全厂热效率相对变化率的计算方法
发电系统运行过程中,当构成它的任意一个子系统或热力设备的分热效率单独变动时,考虑到全厂热效率的提高意味着能耗率降低这一普遍规律,热耗率、发电标准煤耗率、全厂热效率的相对变化率与各子系统热效率相对变化率之间的普适关系式[14]可以写为:

(9)
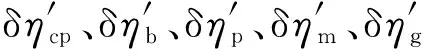
式(9)表明,当任意一个分热效率单独发生变动时,它们的相对变化率的绝对值是相同的,但绝对变化量不同。此时,可以通过计算汽轮机循环热效率的相对变化率,再按照式(6)~式(8)来计算其他能效指标的绝对变化量,汽轮机循环热效率相对变化率的计算可依据参考文献[3]和文献[4]进行,在此不详细展开。
目前,多数电厂的节能工作都是根据式(6)~式(9)进一步求出全厂热效率、热耗率和发电标准煤耗率的相对和绝对变化量,以指导全厂节能减排工作。然而,在实际运行中,促使机组偏离基准工况运行的效率扰动源可能是单一的,也可能是多种扰动源同时存在且相互耦合作用的; 同时,单一扰动可能引起单个热力设备效率发生变化,也可能引起多个热力设备效率同时发生变化。因此,依据子系统或热力设备的分效率单独变化而得出的结果并不能全面反映发电系统运行能效的实际情况,综合系统的运行性能不一定是最优的。因此,建立多效率扰动下发电系统运行能效的分析计算模型是电厂实现深度节能增效亟待解决的一个关键问题。
3 多效率扰动下全厂热效率相对变化率的计算方法
多效率扰动条件下,计算综合系统能效指标的首要工作是求得全厂热效率的相对变化率。为使导出结果具有普适性,对于图1所示的电厂原则性热力系统,设某一运行工况下影响机组热经济性的各个参数或因素分别为x1、x2、x3、x4、…、xb、xp、xi、xm、xg(包括非运行和运行因素,非运行因素主要有煤质、送风温度和循环水温度等,运行因素主要有氧量、主蒸汽压力和温度、再热蒸汽压力和温度等)。假定各参数间相互独立、线性无关,且函数连续可导,微分计算过程中忽略高阶无穷小量。则锅炉热效率ηb、管道热效率ηp、汽轮机循环热效率ηi、机械效率ηm、发电机效率ηg和全厂热效率ηcp可表示为如下多元函数:
ηb=fb(x1,x2,x3,…,xb)
(10)
ηp=fp(x2,x3,x4,…,xp)
(11)
ηi=fi(x3,x4,x5,…,xi)
(12)
ηm=fm(x4,x5,x6,…,xm)
(13)
ηg=fg(x5,x6,x7,…,xg)
(14)
ηcp=ηbηpηiηmηg=fb(x1,x2,x3,…,xb)×
fp(x2,x3,x4,…,xp)×fi(x3,x4,x5,…,xi)×
fm(x4,x5,x6,…,xm)×fg(x5,x6,x7,…,xg)
(15)
3.1 2个分效率同时发生变化

(16)
(17)
则全厂热效率为:

(18)
其中,
Fimg(x)=fi(x3,x4,x5,…,xi)×fm(x4,x5,x6,…,xm)×fg(x5,x6,x7,…,xg)
(19)
全厂热效率、锅炉热效率以及管道热效率的绝对变化量分别为:
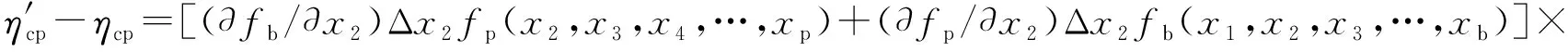
Fimg(x)
(20)
(21)
(22)
由此可得锅炉热效率和管道热效率的相对变化率之和为:

(23)
全厂热效率的相对变化率为:

(24)

(25)
由式(25)可知,当参数x2变化引起锅炉热效率ηb和管道热效率ηp变化而其他热力设备的热效率不发生改变时,全厂热效率的相对变化率近似等于锅炉热效率和管道热效率的相对变化率之和。
可以推理得出,在电厂实际运行过程中,当某些参数变化引起任意2个子系统或热力设备的热效率发生变化而其他子系统或热力设备的热效率不变时,全厂热效率的相对变化率近似等于这2个子系统或热力设备分效率的相对变化率之和。
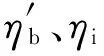
(26)
它们的绝对变化量分别为:
(27)
它们的相对变化率分别为:
(28)
将式(27)和式(28)代入式(26),经数学推导,得:

(29)
又因为
(30)
联立式(29)和式(30),推导并整理可得:
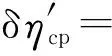
(31)

(32)
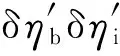
(33)
由式(33)可得出如下结论:当ηp、ηm和ηg为固定值时,锅炉热效率和汽轮机循环热效率同时发生变化的情况下,全厂热效率的相对变化率近似等于锅炉热效率相对变化率与汽轮机循环热效率相对变化率之和。
3.2 3个分效率及以上同时发生变化

(34)
(35)
(36)

(37)
式(37)中:
Fmg(x)=fm(x4,x5,x6,…,xm)×fg(x5,x6,
x7,…,xg)
(38)
全厂热效率、锅炉热效率、管道热效率和汽轮机循环热效率的绝对变化量分别为:

fb(x1,x2,x3,…,xb)fi(x3,x4,x5,…,xi)+
(∂fi/∂x3)Δx3fb(x1,x2,x3,…,xb)×
fp(x2,x3,x4,…,xp)]Fmg(x)
(39)
(40)
(41)
(42)
由此可得锅炉热效率、管道热效率和汽轮机循环热效率的相对变化率之和为:

(43)
则全厂热效率的相对变化率为:
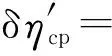
(44)


(45)
由式(45)可知,当参数x3变化引起ηb、ηp和ηi变化,而其他热效率不发生改变时,全厂热效率的相对变化率近似等于ηb、ηp和ηi的相对变化率之和。
同理,电厂实际运行过程中,当某些参数变化引起任意3个子系统或热力设备的热效率同时变化而其他子系统或热力设备的热效率不变时,全厂热效率的相对变化率近似等于这3个子系统或热力设备分效率的相对变化率之和。
当机组运行过程中因运行参数变化引起ηb、ηp、ηi、ηm和ηg中的4个或5个分效率同时变化时,采用同样的方法,可以推得如下关系式:

(46)

(47)

(48)

(49)

(50)
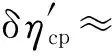
(51)
由式(46)~式(51)可得出如下结论:当因运行参数变化引起ηb、ηp、ηi、ηm和ηg中的4个或5个分效率同时发生变化时,全厂热效率的相对变化率近似等于相应的4个或5个分效率的相对变化率之和。
需要说明的是,上述公式是以电厂原则性热力系统为对象导出的,但其结果也适用于钢铁、冶金和石化等行业系统运行能效的分析和评价。当采用热力学第二定律的方法来进行系统能效评价时,其结果也是适用的。因此,上述方法具有一定的普适性。
4 误差分析
前述多效率扰动时电厂热力系统能效分析计算模型是在忽略高阶无穷小的情况下导出的,为此,需要对该模型进行误差分析,以验证本文所构建的计算模型能否满足工程应用的需要。实际值采用变化后的各子系统分效率的连乘积进行计算,计算值采用本文构建的多效率扰动下复杂热力系统能效分析与评价方法得出。
4.1 分效率同时变化时的误差分析
分效率同时变化时,全厂热效率实际值与计算值之间的误差数据见表2~表5。由表2~表5可以看出,保持各子系统的分效率初始值不变,多个分效率同时变化时,全厂热效率计算值与实际值误差较小,近似一致。同时,分效率的变化幅度越大、变化个数越多,全厂热效率计算值与实际值的偏差也越大。当5个分效率同时变化,且各个分效率变化幅度均为0.6%时,全厂热效率计算值与实际值的偏差最大,但其绝对误差仅为0.000 239,相对误差为0.055 8%,完全满足工程实际应用要求。

表2 2个分效率同时变化时的误差计算数据1)Tab.2 Calculated error data for simultaneous changes in two sub-efficiencies

表3 3个分效率同时变化时的误差计算数据1)Tab.3 Calculated error data for simultaneous changes in three sub-efficiencies

表4 4个分效率同时变化时的误差计算数据1)Tab.4 Calculated error data for simultaneous changes in four sub-efficiencies

表5 5个分效率同时变化时的误差计算数据1)Tab.5 Calculated error data for simultaneous changes in five sub-efficiencies
4.2 不同分效率初始值情况下,分效率同时变化0.2%时的误差分析
在工程实际应用中,较少出现多个分效率同时变化较大的情况,而多个分效率基于初始值小范围波动的情况较为常见。表6~表9给出了分效率同时变化2%时的误差计算数据。由表6~表9可知,在各个分效率初始值不同的情况下,得到的全厂热效率计算值与实际值误差较小,近乎一致。分效率变化的个数越多、初始值越大,全厂热效率计算值与实际值的偏差也越大。当各个分效率初始值分别为ηb=95%、ηp=98.5%、ηi=47.5%、ηm=99.5%、ηg=99.5%,各分效率同时变化0.2%时,全厂热效率计算值与实际值的偏差最大,其绝对误差为0.000 026 5,相对误差为0.005 96%,满足工程实际应用要求。

表6 2个分效率同时变化0.2%时的误差计算数据1)Tab.6 Calculated error data for a simultaneous 0.2% variation in two sub-efficiencies

表7 3个分效率同时变化0.2%时的误差计算数据1)Tab.7 Calculated error data for a simultaneous 0.2% variation in three sub-efficiencies

表8 4个分效率同时变化0.2%时的误差计算数据1)Tab.8 Calculated error data for a simultaneous 0.2% variation in four sub-efficiencies

表9 5个分效率同时变化0.2%时的误差计算数据Tab.9 Calculated error data for a simultaneous 0.2% variation in five sub-efficiencies
从误差分析结果可以看出,分效率同时变化的个数越多,对全厂热效率的影响权重就越大。因此,仅考虑单个热效率扰动来进行综合系统能效分析与评价是不科学的,只有在多效率扰动条件下进行综合系统能效分析与评价,才能科学评价综合系统的运行能效,进而促进综合系统的节能增效。
5 结 论
(1) 对于单热效率扰动,全厂热效率的相对变化率等于各子系统或热力设备分效率的相对变化率。
(2) 经过严谨的数学推演,导出了多效率扰动条件下全厂热效率的相对变化率等于相关子系统或热力设备分效率的相对变化率之和;通过误差分析,验证了据此进行电厂运行能效的分析与评价更符合现场实际情况。该方法可以定量计算出多个子系统或热力设备的分效率同时变化时对全厂热效率的影响规律及其权重大小,进而可计算出电厂热耗率、煤耗率等能效评价指标的大小及其分布规律,为协调优化各热力设备提供了理论支撑。
(3) 根据误差分析结果,分效率同时变化的个数越多,对全厂热效率的影响权重就越大。因此,只考虑单效率扰动来进行综合系统的能效分析与评价难以促进复杂热力系统深度节能。本文所建立的多效率扰动下电厂热力系统能效分析与评价模型也适用于其他行业由多个子系统构成的复杂热力系统。若采用热力学第二定律来分析,按照同样的处理手段,也可以得出类似的计算模型。

