带局部运动表面翼型的动态失速特性研究

张馨艺， 孙晓晶

(1.上海理工大学 能源与动力工程学院，上海 200093；2.上海市动力工程多相流动与传热重点实验室，上海 200093)

动态失速是一种非定常的失速延迟流动分离现象[1-3]，该现象的产生主要是由于前缘脱体涡的形成、快速后移以及脱落引起压力中心后移，致使升力减小、阻力增大，翼型扭转载荷增大，会严重破坏流场的稳定性[4-5]。为降低动态失速引起的不利影响，研究人员提出了多种主动控制方法。Kaufmann等[6]在OA209直升机翼型吸力面的不同位置布置了回流襟翼，结果发现在合适的位置施加襟翼控制可抑制动态失速涡，改善动态失速特性。陈微圣等[7]研究了高雷诺数条件下前缘吸气对NACA0012翼型动态失速特性的影响。由于主动控制方法可根据实际需求调节参数来控制流场[8]，因此相较于被动控制方法，主动控制方法备受重视。

运动表面边界层控制是一种主动控制方法，通过向边界层注入附加动量，使边界层邻近区域的流动加速，可减小表面与自由来流之间的相对运动，缩小流动分离区域，从而使升力系数增大、阻力系数减小。Modi等[9]采用2个旋转圆柱体作为运动表面，得到了不同迎角和速度比下二维平板的阻力系数，结果表明，随着速度比的增大，平板的阻力系数减小，延迟了边界层的分离。AL-Garni等[10]针对以前缘旋转圆柱体为运动表面的NACA0024翼型进行了实验研究。庄月晴等[11]采用数值模拟的方法研究了沿顺时针方向S809翼型表面运动的气动性能，结果表明，翼型表面运动能有效抑制大攻角下叶片表面的流动分离。Salimipour等[12]研究了运动表面的位置和速度对S809翼型流动特性的影响，并对三叶水平轴风力机的性能进行了数值分析，发现布置有运动表面的水平轴风力机具有更高的风能利用率。

目前，国内外对于运动表面边界层控制方法(MSBC)已有所研究，但对于MSBC作用下动态失速的研究还尚未见报道。笔者以NACA0012翼型为研究对象，基于Transition SST模型计算分析了运动表面的位置、长度、速度以及槽的深度对NACA0012翼型在振荡条件下动态失速特性的影响，并与同工况下采用射流方法[13]时的控制效果及能耗进行了对比。

1 数值方法与验证

1.1 MSBC翼型

在翼型吸力面不同位置开设不同长度的凹槽，以永磁同步电机驱动的皮带表面作为运动表面，运动表面的动力系统由永磁同步电机、变频器和控制系统组成，动力主体为永磁同步电机，控制部件为变频器，控制系统实时调整永磁同步电机的运行参数[14]。图1为带局部运动表面的NACA0012翼型(简称MSBC翼型)示意图。其中，弦长c为1 m，基于弦长的来流雷诺数为106，s和l分别为运动表面的无量纲位置和无量纲长度，k为运动表面与自由来流的速度比(简称速度比)，h为凹槽深度。

(1)

(2)

(3)

图1 MSBC翼型Fig.1 Geometry of MSBC airfoil

式中：xms为运动表面起始点的横坐标；lms为运动表面的长度；Vms为运动表面的速度；V∞为自由来流的速度。

1.2 边界条件及网格划分

采用O型结构化网格，计算域分为旋转域I和静止域II，如图2所示。旋转域I的半径为5c，为确保壁面第1层网格的无量纲壁面距离Y+≈1，第1层网格高度设置为2×10-5。静止域II的半径为70c，旋转域I与静止域II通过交界面相接。进口边界条件设置为速度进口，出口边界条件为压力出口，翼型表面和运动表面均设置为无滑移壁面。翼型和运动表面的运动分别通过滑移网格技术和用户自定义程序(UDF)来实现。

(a) 边界条件

(b) 局部网格

翼型绕1/4弦长进行周期性俯仰运动，其方程如下：

a=a0+Asin(2πft)

(4)

式中：a为瞬时攻角；a0为平均攻角，取14.85°；A为振幅角，取9.89°；f为频率；t为时间。

折合频率K和气动力系数为：

(5)

(6)

(7)

式中：Cl为升力系数；Cd为阻力系数；Fl为翼型的升力；Fd为翼型的阻力；ρ∞为来流的密度。

1.3 网格无关性验证

为减少计算量，提高计算精准度，通过改变翼型周向和计算域径向的网格数来改变网格的疏密程度。对不同疏密的网格进行了无关性验证，结果见图3。由图3可知，网格数为18万和36万时翼型气动力系数的计算结果基本吻合。因此，选取网格数为18万。

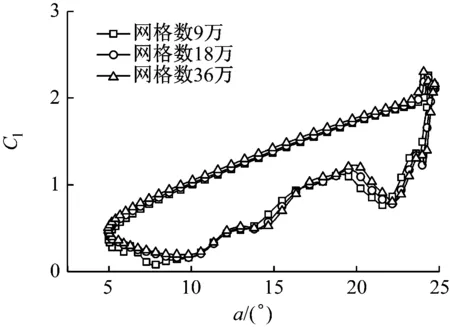
(a) 升力系数

(b) 阻力系数

1.4 数值模型可靠性验证

通过将本文的模拟结果与美国航空航天局(NASA)的风洞实验数据[15]以及文献[13]中的模拟结果进行对比，来验证模型的准确性。经过网格和时间步长无关性验证后，时间步长设置为10-4s，网格数为18万。Transition SST模型考虑了边界层从层流到湍流的转捩过程[7,16]，计算准确性得到提高，故采用Transition SST模型。如图4所示，在小攻角下气动力系数模拟值与实验值基本一致，随着攻角的增大，受Transition SST模型的限制，气动力系数模拟值与实验值之间的差别逐渐明显，但平均偏差小于15%，且变化趋势基本一致[16]。因此，模拟所采用的网格和计算方法具有较高的可靠性和准确性。

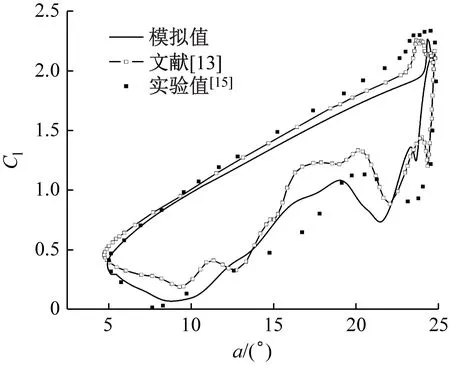
(a) 升力系数

(b) 阻力系数

(c) 力矩系数Cm

2 运动表面对翼型动态失速特性的影响

运动表面的摩擦力系数Cdms和耗能系数Cpc[12]分别定义为：

(8)

(9)

式中：Fdms为运动表面的摩擦力。

将运动表面的能耗看作阻力的一种表现形式，故运动表面的等效升阻比ηms定义为：

(10)

2.1 运动表面位置的影响

保持l=0.1、k=1和h=1 mm不变，在翼型吸力面距前缘点0.02c～0.5c的位置上布置运动表面，研究不同运动表面位置对动态失速特性的影响。原始翼型的平均升阻比为15.498，最大升力系数为2.117，最小阻力系数为0.001 91。

图5给出了不同运动表面位置的MSBC翼型与原始翼型(BASE)气动力系数的对比结果。由图5可知，与原始翼型相比，在上仰阶段， MSBC翼型的升力系数增大，阻力系数减小，等效升阻比有所提升；在下俯阶段，MSBC翼型的升力系数增大，在大攻角下阻力系数增大，在小攻角下阻力系数减小，因此在小攻角下等效升阻比有较大提升。与原始翼型相比，MSBC翼型气动力迟滞环的面积减小，气动力迟滞现象有所改善。

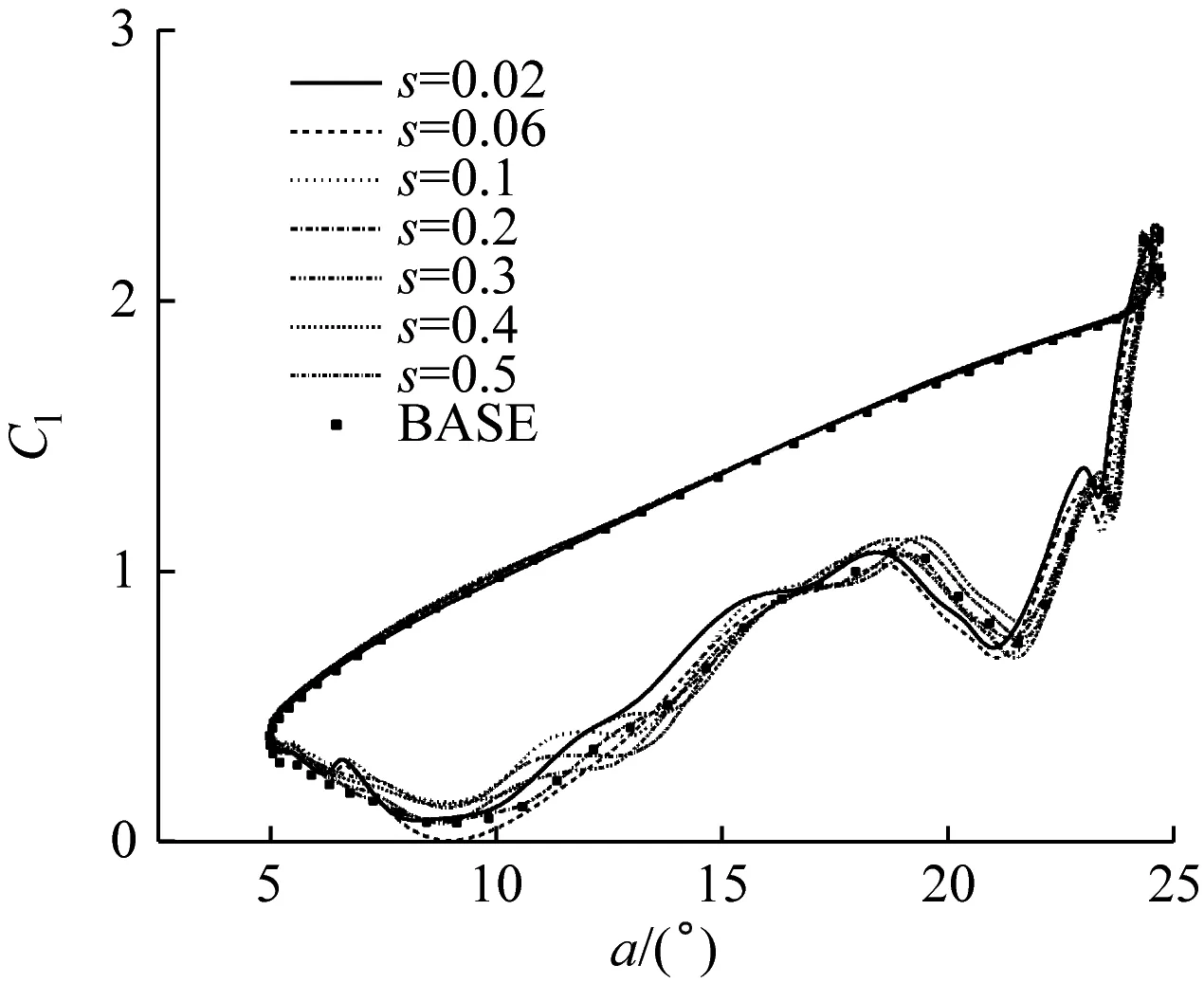
(a) 升力系数

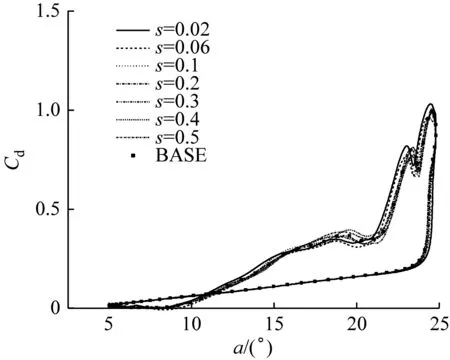
(b) 阻力系数

对于不同运动表面位置的MSBC翼型，根据等效升阻比，s=0.4的运动表面对动态失速的控制效果最好，此时平均升阻比为22.675，最大升力系数为2.250，等效升阻比为19.436，较原始翼型分别增大46.30%、6.28%和25.40%；最小阻力系数为0.000 7，较原始翼型减小63.35%。

图6为不同位置的运动表面处于静止状态时MSBC翼型和原始翼型的升阻比曲线。当s分别为0.04和0.06时，MSBC翼型的平均升阻比分别为11.948和12.46，与原始翼型相比均有所减小；s=0.4的MSBC翼型的平均升阻比为15.648，较原始翼型略有增大。在小攻角下，运动表面越靠近前缘的MSBC翼型的升阻比越小。这是由于凹槽的存在破坏了MSBC翼型的外形，使气动效率降低。因此，运动表面靠近前缘的MSBC翼型对动态失速的控制效果不及运动表面靠近中部的MSBC翼型。

图6 不同位置的运动表面处于静止状态时MSBC翼型和原始翼型的升阻比Fig.6 Lift-to-drag ratio of MSBC airfoil and original airfoil at static station with different positions

2.2 速度比的影响

保持s=0.4、l=0.1和h=1 mm不变，研究不同速度比k下运动表面对动态失速特性的影响。图7为不同速度比下MSBC翼型和原始翼型气动力系数的变化。由图7可知，随着速度比的增加，升力系数增幅越明显，在上仰阶段阻力系数逐渐减小，在下俯阶段阻力系数逐渐增大。当k=4时，MSBC翼型的平均升力系数为1.162，较原始翼型增大10.03%。速度比越大，迟滞环面积越小，运动表面对动态失速的改善效果越好。

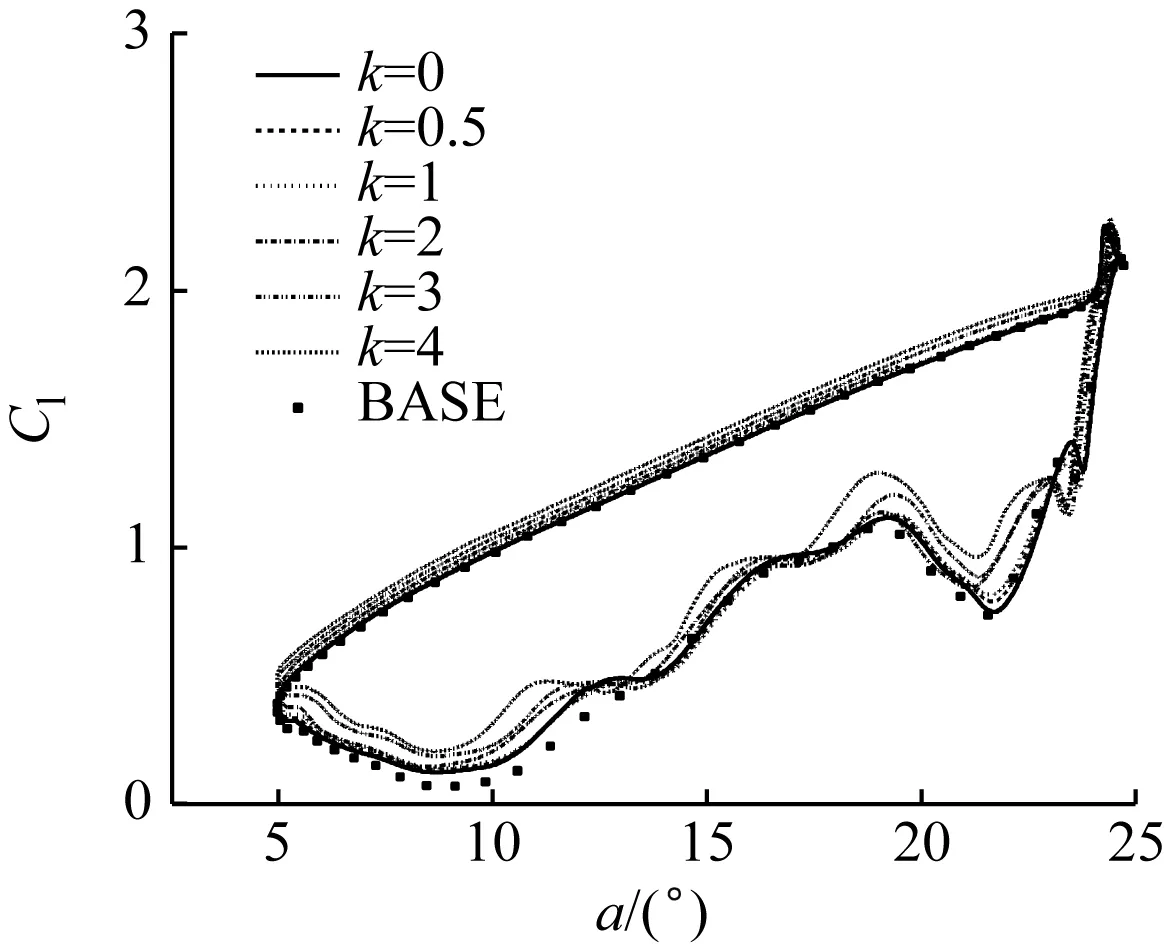
(a) 升力系数

(b) 阻力系数

结合能耗，当k分别为0.5、1、2、3和4时，MSBC翼型的等效升阻比分别为17.628、19.436、16.371、12.679和10.062，较原始翼型分别变化13.74%、25.40%、5.63%、-18.19%和-35.07%。由此得出，随着速度比的增加，运动表面对翼型气动性能的改善效果逐渐提高，但速度比越大，能耗越大。综上，当k=1时可使翼型的净获能效率最大化。

2.3 运动表面长度的影响

保持s=0.4、k=1和h=1 mm不变，研究不同长度的运动表面对动态失速特性的影响。图8给出了不同运动表面长度的MSBC翼型与原始翼型气动力系数的对比。随着MSBC翼型运动表面长度的增加，在上仰阶段升力系数增大，阻力系数减小；在下俯阶段升力系数和阻力系数均增大。运动表面长度越大，MSBC翼型对动态失速的控制效果越好。l=0.5时MSBC翼型的最大升力系数较原始翼型增大8.9%，最小阻力系数减小63.8%。在攻角为13°～20°，l=0.2时MSBC翼型的升力系数和阻力系数均达到最大。l分别为0.1、0.2、0.3、0.4和0.5时，MSBC翼型的等效升阻比分别为19.436、20.903、25.354、26.381和25.835，较原始翼型分别增大25.4%、34.8%、63.5%、70.2%和66.6%，由此可知，运动表面长度为0.4 m时MSBC对翼型的动态失速具有最佳的控制效果。

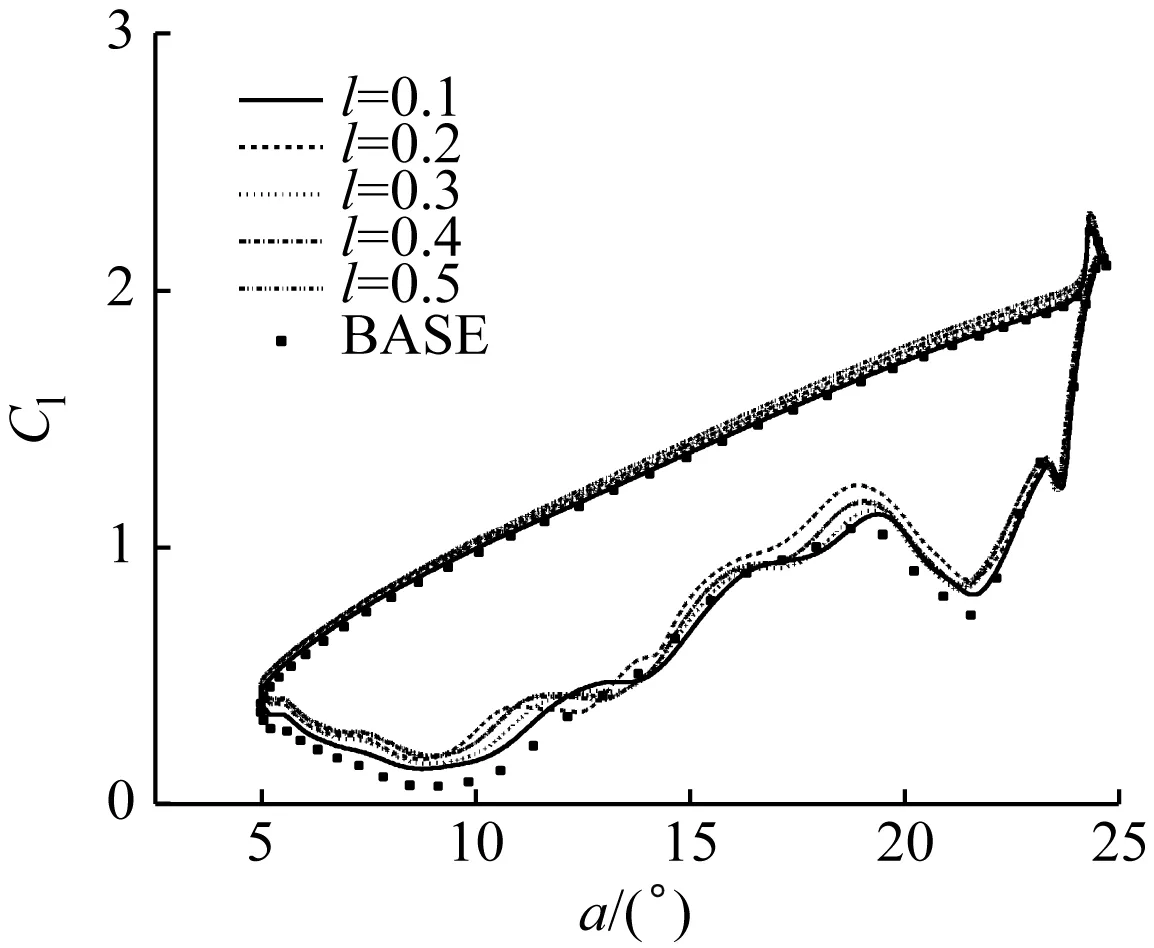
(a) 升力系数

(b) 阻力系数

图9为MSBC翼型和原始翼型在不同时刻的流场图。其中，MSBC翼型的参数为s=0.4、l=0.4、k=1和h=1 mm。对于原始翼型，在翼型上仰至23°之前，翼型表面的流动保持附着状态；当翼型上仰至23.95°时，翼型尾缘出现流动分离；随着翼型继续上仰，流动分离逐渐向前缘延伸，上仰至24.47°时在翼型前缘出现了前缘涡；随着前缘涡的弦向运动，上仰至24.73°时在翼型前缘诱发产生了二次涡；之后，翼型开始进行下俯运动，前缘涡与二次涡融合，逐渐脱离翼型表面，并在翼型尾缘再次形成尾缘涡。前缘涡和尾缘涡交替生成、发展和脱落，并交替占据翼型表面旋涡的主体地位，从而引起翼型气动力系数的剧烈变化。翼型下俯至21.16°时，在吸力面中后部产生1个小涡；当翼型继续下俯至14.94°时，其表面仍存在旋涡，并不断向翼型尾缘移动，直至气流重新附着。

图9 不同时刻下MSBC翼型和原始翼型的流场图Fig.9 Flow field diagram of MSBC airfoil and original airfoil at different moments

对于MSBC翼型，在翼型上仰至23°之前未发生流动分离，因此MSBC对周围流场没有显著的控制效果；当翼型上仰至23.95°时MSBC翼型的流动分离区域较原始翼型略小；当翼型下俯至21.16°时，MSBC抑制了小涡的产生；当翼型继续下俯至14.94°时，MSBC翼型尾部的尾缘涡尺寸比原始翼型小，且气流重新开始附着于翼型表面，而原始翼型还未开始附着；当翼型下俯至12.43°时，在运动表面位置出现1个涡；当翼型下俯至8.36°时，MSBC翼型吸力面的流动分离现象基本消失，气流重新附着在翼型表面，而原始翼型尾部气流还未完全附着，故运动表面加快了气流重新附着的速度。在小攻角下，MSBC对动态失速有明显的控制效果。

图10为不同时刻下MSBC翼型和原始翼型的表面压力系数(Cp)曲线。当MSBC翼型下俯至21.16°时，其前缘吸力面的压力系数峰值较原始翼型减小7.84%，而其后缘吸力面的压力增大，导致后缘吸力面的压差较压力面减小，结合图9(f)可知，此时前缘压差增大对升力系数增大的影响大于对后缘压差减小的影响。当MSBC翼型下俯至14.94°时，其后缘压差增大，这是由于运动表面使尾部尾缘涡的尺度和强度减小。当MSBC翼型下俯至8.36°时，其吸力面压力系数峰值较原始翼型减小16.86%，且前缘吸力面有较强的低压区。

(a) 21.16°、下俯

(b) 14.94°、下俯

(c) 8.36°、下俯

2.4 凹槽深度的影响

保持s=0.4、l=0.1和k=1不变，研究不同凹槽深度对动态失速特性的影响。图11给出了不同凹槽深度的MSBC翼型与原始翼型气动力系数的对比。从图11可以看出，MSBC翼型的凹槽深度越大，上仰阶段升力系数越小，阻力系数越大；在下俯阶段，大攻角下升力系数和阻力系数较原始翼型均减小。凹槽的存在破坏了翼型表面的气动性能，凹槽越深，MSBC控制作用越不明显，凹槽深度为0.25 mm时MSBC翼型的等效升阻比最大，较原始翼型增大43.03%。

(a) 升力系数

(b) 阻力系数

综上，s=0.4、l=0.4、k=1和h=0.25 mm时MSBC对动态失速的控制效果最好。

3 表面射流和运动表面对动态失速的影响

在相同工况(雷诺数Re=106)下针对运动表面和表面射流对动态失速的影响进行对比研究。运动表面布置在翼型吸力面距前缘0.4c的位置，其宽度为0.4c。根据文献[13]的研究结果，射流口设置在距前缘点4%c时，射流的流动控制效果最佳。图12给出了带表面射流、MSBC翼型以及原始翼型气动力系数的变化。采用表面射流控制方式时，当射流速度为14.315 2 m/s、耗能系数为0.002时，在翼型上仰阶段，其升力系数和阻力系数较原始翼型均略减小，平均升阻比为12.408，较原始翼型减小20%，较MSBC翼型减小35.5%；在翼型下俯阶段，翼型的升力系数明显增大，但阻力系数在20°～25°攻角范围内增幅也较大。对于MSBC翼型，当其运动表面速度为14.315 2 m/s、耗能系数为0.002时，MSBC翼型在上仰阶段和下俯阶段的气动性能均能得到提升。

(a) 升力系数

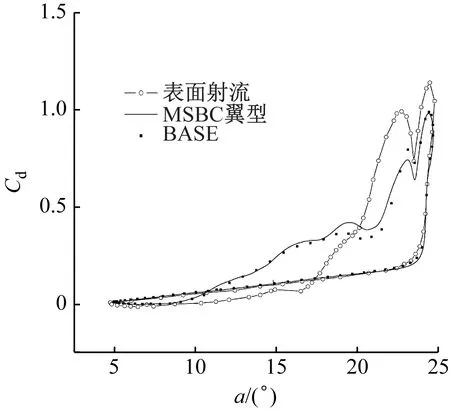
(b) 阻力系数

根据文献[17]，采用耗能系数Pc来定义射流所消耗的能量。

(11)

式中：Vjet为喷气口处的射流速度；Ajet为射流口截面积；S为二维中翼型弦长；ρjet为射流密度。

射流介质与来流介质相同，所以ρjet与ρ∞相同。结合能耗，射流的等效升阻比定义为：

(12)

图13给出了带表面射流、MSBC翼型以及原始翼型等效升阻比的对比结果。在上仰阶段，MSBC翼型的等效升阻比最大，带表面射流翼型的等效升阻比最小；在下俯阶段中，MSBC翼型的等效升阻比最大，其次是带表面射流的翼型。在上仰阶段、下俯阶段和全程运动中，MSBC翼型的等效升阻比较带表面射流的翼型分别增大了37.81%、43.30%和29.64%，较原始翼型分别增大了17.25%、72.52%和57.10%。因此，在能耗较低的情况下，与采用表面射流相比，运动表面可以通过输入较少的局部能量对动态失速具有更好的控制效果，提升翼型的气动效率。

图13 带表面射流、MSBC翼型以及原始翼型等效升阻比的对比Fig.13 Comparison of the equivalent lift-to-drag ratios of airfoil with surface jet, MSBC airfoil and original airfoil

4 结 论

(1) 综合来看，s=0.4、l=0.4、k=1和h=0.25 mm时MSBC对动态失速的控制效果最好，其等效升阻比较原始翼型增大了57.10%。

(2) 采用MSBC翼型可使尾部尾缘涡的尺度和强度减小，加快气流重新附着于翼型表面的速度。

(3) 在低耗能系数条件下，MSBC翼型在俯仰阶段的等效升阻比较带表面射流的翼型增大了29.64%，表明与传统表面射流控制方法相比，运动表面可通过较少的局部能量输入更好地抑制动态失速现象。