超临界受热面水侧颗粒沉积的数值模拟研究

曾子轮， 王 超， 李鸿源， 黎宇航， 徐 鸿

(华北电力大学 电站能量传递转化与系统教育部重点实验室， 北京 102206)

目前，国内超(超)临界燃煤机组存量巨大，但随着 “碳中和”目标的提出，燃煤机组亟需寻找新的出路。丛星亮等[1]研究表明660 MW超超临界二次再热机组深度调峰的能量损失在15%左右，低于抽水蓄能的25%。因此，除政策要求外，燃煤机组以提供调峰服务为主要产品的经济学可行性亦得到论证。

因此，超(超)临界机组的运行可靠性将越发重要，但相较于亚临界机组，其对于汽水侧沉积物也更为敏感。研究表明[2-3]，在以超临界水为动力工质的系统中，沉积物主要来自低温给水管道腐蚀所产生的Fe离子，且溶解在水中的盐可能存在2种壁面沉积方式，即以颗粒的形式堆积或直接在壁面结晶。

同时，颗粒沉积的主要过程为颗粒由主流区向近壁面运动的过程。近壁面流场对颗粒沉积起决定作用[4-5]，且加热引起的浮力效应和热加速度明显影响近壁面流体流动[6]。特别在跨临界区，工质物性参数剧烈变化，上述影响加剧，使颗粒在跨临界区的沉积规律变得非常不明确。

为了研究跨临界区颗粒沉积与湍流流场之间的关系，笔者首先明确了适用于超临界水传热的湍流模型，并利用Fluent中的离散相 (DPM)模型对颗粒沉积进行数值模拟。结合Karakama等[7]的颗粒沉积实验，以颗粒在壁面的质量通量作为沉积通量，分析了壁面全捕捉(trap)和全反射(reflect)2种极限条件下颗粒在壁面的沉积规律。

1 模型选择

1.1 跨临界湍流模型选择

近年来，研究人员开展了大量基于雷诺平均方法的跨伪临界区湍流模拟研究[8-11]，由于超临界水的高黏特性，虽然模拟结果对于其他超临界流体表现出较好的预测效果，但对于超临界水仍存在较大误差。

超临界水湍流模拟中最特殊的一类情况为流体传热恶化模拟，目前鲜有文献的模拟结果能够完美预测实验值，均存在过早预测或预测延迟的问题。如果某一种模型能够较为合理地预测超临界水的传热恶化，那么对于非传热恶化状态的超临界水，该模型也能较好地描述其湍流流动问题。

关于超临界水湍流流动的备选模型和其设置详见表1，其中Prt为近壁面普朗特数，同时通过管内壁温度表征超临界水湍流流动，并利用Mao等[12]的水平圆管传热实验数据对模拟结果进行比较，结果如图1所示，其中q为热流密度，G为质量流速，D为管内径，p为流体压力。

表1 湍流模型的选择Tab.1 Turbulence models

由图1可知，虽然3种模型均存在对于传热恶化预测的提前或者滞后，但显然RNGk-ε模型误差较大。此外，虽然SSTk-ω模型在轴向位置1.2 ～1.75 m时，内壁温度模拟结果与文献[12]的实验值一致。但该模型在轴向位置0.25 m时，预测结果严重失真。故其并不适用超临界水的传热模拟。

图1 水平管中超临界水传热模型的对比Fig.1 Comparison of heat transfer models for SCW in horizontal tubes

相较之下，Realizablek-ε模型虽然也存在提前预测的情况，但该模型模拟结果中，内壁温度沿轴向的上升趋势与实验值一致，同时该模型预测的传热恶化峰值温度也与实验值高度吻合。

在大管径情况下，若水平管出现传热恶化现象，此时上表面的壁面温度往往高于下表面，这主要是由于重力对于流场的影响，进而对上壁面与流体的换热产生抑制作用导致的。图2给出了参照Karakama的颗粒沉积实验条件相关参数，分析小管径情况下重力对流体流动的影响，其中Tin为流体入口温度。

从图2可以看出，不管是否考虑重力，水平管内上下表面的壁面温度差异并不明显，且模拟结果与实验值吻合度较高。相较于其他大管径高热流密度的水平管表现出较大的上下壁面温差[13]，在低热流密度的细管中，重力对流体流动的影响几乎可以忽略。

从图2还可以看出，在跨临界温度(Tpc=380 ℃)附近，并未出现明显的传热恶化。同时，浮力因素在周向的影响亦可以忽略。

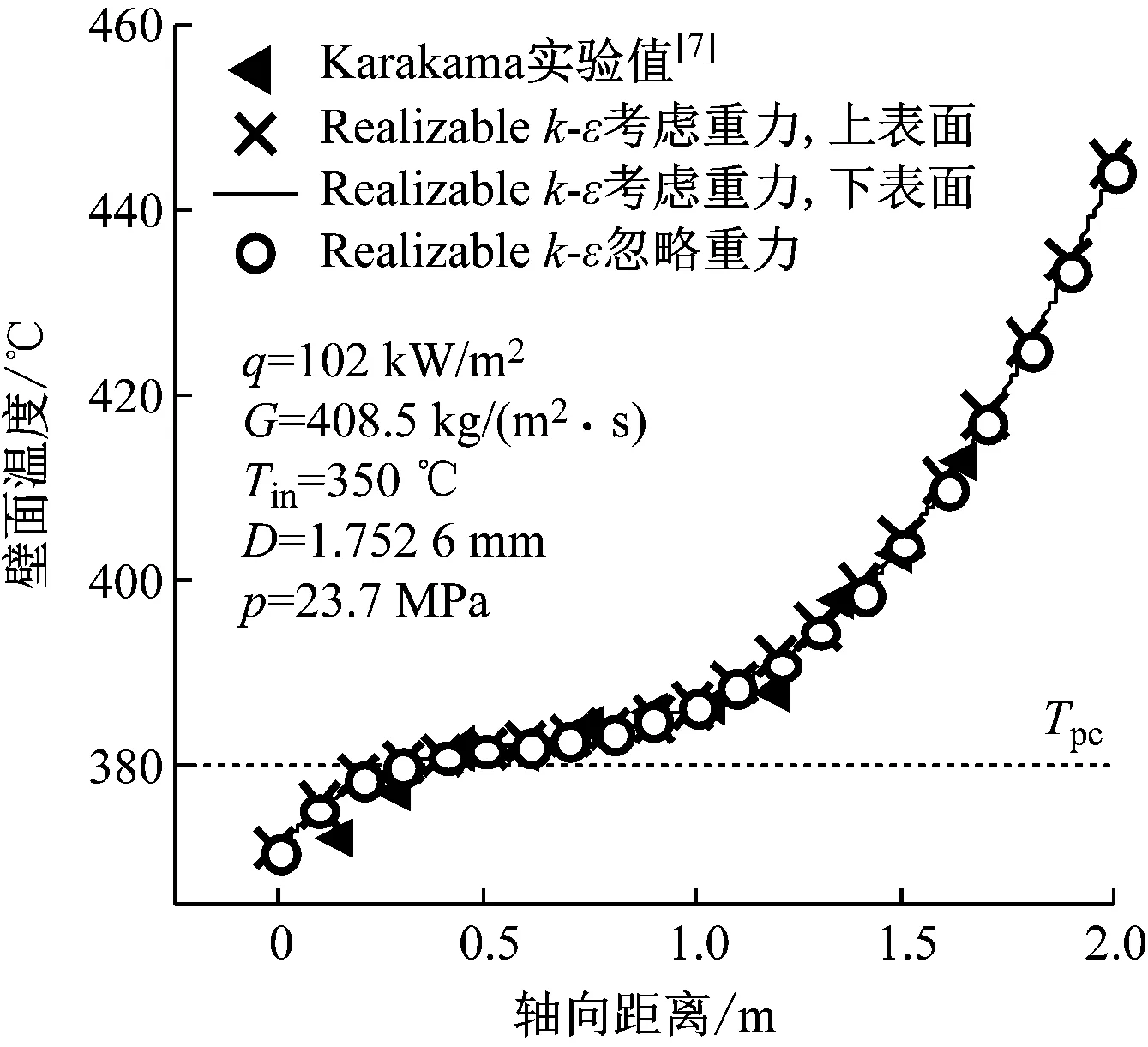
图2 重力对水平管上下外壁面温度的影响Fig.2 Effect of gravity on the upper and lower wall temperature of the horizontal tube

1.2 颗粒沉积数值模拟

1.2.1 边界条件设置

利用Fluent DPM模型模拟颗粒在流场中的运动，尺寸参照Karakama实验段，即壁厚δ=0.711 2 mm(0.028英寸)，内径D=1.752 6 mm(0.069英寸)，因换热管为水平光滑细长圆管，故采用2D建模以节省算力。

流体恒定参数为：G=408.5 kg/(m2·s)，Tin=350 ℃，p= 23.7 MPa,q=102 kW/m2，加热段长度为2 000 mm。为避免入口效应，加热段前设入口段长度L=40 mm。

在DPM模型中，颗粒默认正球形，入口段壁面条件设置为反射条件，加热段壁面设置为捕捉或反射条件，同时考虑颗粒对流体的反作用。

1.2.2 颗粒入射面设置

在Karakama的沉积实验中，含铁颗粒的携带进入方式为掺混高浓度含铁离子溶液，在超临界水中氧化并析出形成颗粒，该过程包含颗粒氧化还原的化学反应和颗粒运动的物理规律。目前，两者特性均不明确且存在复杂的相互作用，为关注颗粒运动，需建立等效射入面，排除化学反应的影响。

含铁溶液在缺氧条件下氧化还原主要生成Fe3O4颗粒，目前还鲜有得到完整验证的动力学描述，故成核速率k用Arrhenius方程[14]表示：

(1)

式中：B为指前因子；kB为玻尔兹曼常数；γ为表面张力，N/m；Vm为粒子体积，m3；T为温度，K;s为饱和度。

因超临界水表面张力未知，通过温度与相对成核速率的关系，选择较为合适的γ值。当γ=1×10-26N/m时，成核速率在350～380 ℃内近似匀速，符合物理规律。此时，颗粒在该温度区间内等概率地生成，且颗粒在升温时发生合并、凝聚。因为流场边界层的特性，可以假设颗粒仅在主流区析出，故取350 ℃等温线与黏性子层交点为入射面起始点，将流体中心温度达到380 ℃的位置作为颗粒射入的终点，2点连线上的温度沿径向的变化近似成线性规律。颗粒入射面几何示意图如图3所示。

图3 颗粒入射面示意图Fig.3 Schematic diagram of particle incidence surface

1.2.3 结果获取与模型验证

提取模拟结果的沉积速率，附加与实验相同的时长，并通过颗粒在壁面的质量通量表征。当粒子与壁面发生相互作用时，壁面的质量通量增加。假设沉积层孔隙率为10%，计算最终形成的沉积厚度。

因为颗粒在与壁面的碰撞中既有可能为完全弹性碰撞，表现出反射特性；也有可能黏附于壁面内侧，表现出捕捉特性。该过程受到多种因素的影响，一般计算时通过假设捕捉率来简化。

由于离子在低于350 ℃时也会氧化析出，排除这一因素后，将沉积厚度进行归一化处理，结果见图4。可以看出，模拟结果的变化趋势与实验值相近，证明前述假设对模拟结果的影响在可接受范围内。

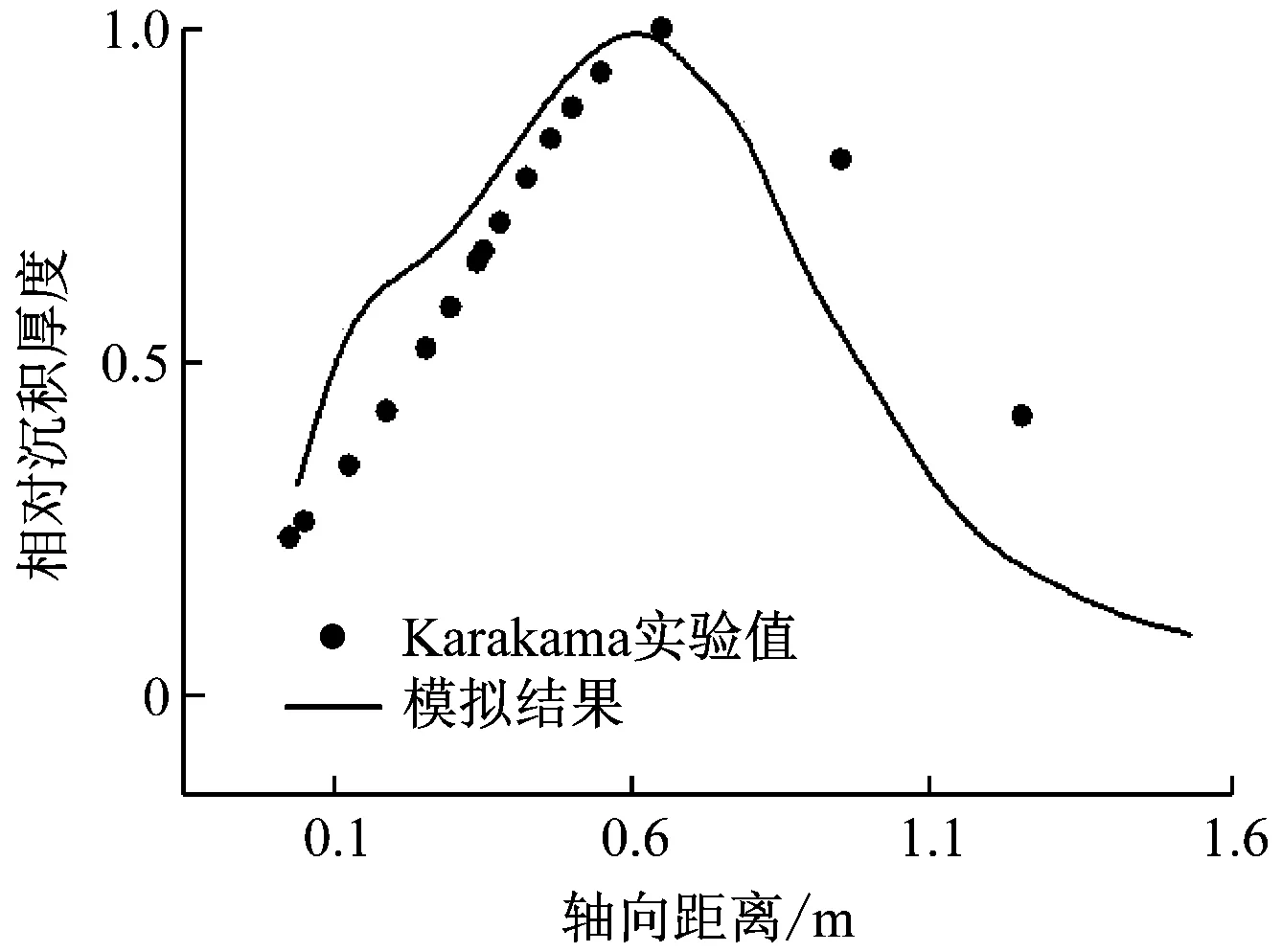
图4 沉积厚度的数值模拟结果与实验值对比Fig.4 Comparison of numerical simulation results and experimental values

2 2种极限情况下的颗粒沉积模拟

由于颗粒运动复杂，因此通过独立分析壁面全捕捉和全反射2种极限情况，并在全反射壁面情况下考虑热泳力对颗粒运动是否有影响，有利于掌握颗粒在流体中的运动规律。

2.1 捕捉壁面条件下的颗粒沉积

考虑热泳力对颗粒运动的影响，1.0 μm 和4.0 μm 2种粒径dp的沉积模拟如图5所示。从图5可以看出，2种粒径颗粒均在跨临界区(0.25～1.25 m)附近存在较明显的沉积现象，表现出迅速沉积的特性。虽然2种粒径颗粒在初始状态的沉积速率有差别但均相对较小，这可能是因为靠近边界层的温度梯度较大，热泳力影响明显，如式(2)所示。此外，边界层相对较厚，颗粒不能及时从流体流动中获得足够的动能，无法穿透边界层到达壁面完成沉积。

图5 2种粒径条件下沉积厚度的对比Fig.5 Comparison of deposition thickness under two particle sizes

但对于小粒径颗粒，由于受到湍动能的影响，颗粒向壁面的速度逐渐增大，表现出被捕捉的特性。此时流体对于颗粒的作用力占主导地位。同时，随着颗粒凝结点向轴线靠近，颗粒更容易被主流水裹挟，沉积效果减弱。

热泳力FT表达式如下：

(2)

式中：μ为运动黏度；υ为动力黏度；T0为颗粒附近的平均温度；∇T为温度梯度；dp为颗粒半径；kp、kg分别为粒子和流体的导热系数。

对于大粒径颗粒，其质量与半径的三次方正相关，此时重力起主导作用。在近壁面形成的大颗粒迅速沿重力方向沉积于壁面。同时，随着流体逐渐被加热，密度减小，主流场流速增加，流体曳力对颗粒影响逐渐增大，颗粒轴向速度逐渐增加，导致沉积速率均匀下降。之后，随着流体跨过伪临界点，流体密度下降趋势减弱，颗粒与流体的密度差增大幅度放缓，颗粒的沉积速度趋于平缓。此时，随着颗粒沉积，粒子浓度逐渐降低，沉积速度整体表现出下降趋势。

2.2 反射壁面条件下的颗粒沉积

更改壁面条件为全反射，此时模型任意横截面的颗粒平均浓度恒定。

图6给出了0.1 μm 和1.0 μm 2种粒径条件下壁面质量通量分布。由图6可知，虽然入射颗粒的质量浓度相同，但在考虑热泳力的模拟中，1.0 μm粒径颗粒与壁面的质量通量比0.1 μm粒径时更高。但若从碰撞频率角度看，由于直径变化导致的颗粒质量变化，应为0.1 μm颗粒与壁面碰撞频率更高。因此，可以认为质量越小，越容易受到湍流对颗粒运动的影响。这也进一步证明颗粒在流场中的分布差异和自身所受重力与流场对颗粒的影响有关。

(a) dp=0.1 μm

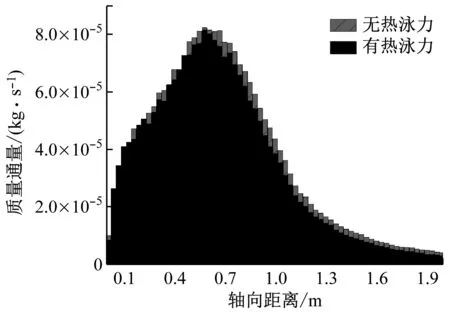
(b) dp=1.0 μm

2种粒径条件下颗粒与壁面形成的质量通量沿轴向的分布均存在明显的峰，这主要是因为颗粒受流体湍动能的影响随时间累积，最终颗粒获得足够的法向速度，与壁面产生相互作用力；颗粒在与壁面完全弹性碰撞后向主流区运动，此时流场温度升高，流体流速增加，颗粒轴向速度增加，最终颗粒被裹挟进入主流水，因此其质量通量逐渐降低。

但相较于1.0 μm粒径颗粒，0.1 μm粒径颗粒的峰值更靠近入射口且峰的宽度更窄，这主要是因为0.1 μm颗粒在入射后的初始动量和质量较小，颗粒受湍流影响明显，其初始动量的方向被迅速改变；同时，小颗粒更容易被裹挟进入主流水，因此质量通量的下降也更明显。

2.3 反射壁面条件下热泳力对颗粒沉积的影响

流场中热泳力也会对颗粒运动产生影响，根据式(2)，热泳力方向始终与温度梯度方向相反，即在本模型中始终由壁面指向圆管中轴线。

图6反映了有无热泳力对颗粒运动的影响，虽然从相对量上考虑，有无热泳力对于大粒径颗粒的影响几乎可以忽略不计，但是对于小粒径颗粒，有无热泳力存在较为明显的差异。这一现象表明，颗粒在流场中的分布差异与自身特性和流场湍流对颗粒的影响有关。

为了更详细地探究热泳力对颗粒运动的影响，图7给出了考虑热泳力时壁面质量通量沿轴向分布的绝对差值。对于0.1 μm粒径颗粒，质量通量在0.4～1.0 m之间出现明显的数量级下降，且该值沿轴向的分布与图6质量通量沿轴向的分布总是在同一数量级；对于1.0 μm粒径颗粒，在热泳力影响下质量通量无数量级变化。但1.0 μm颗粒的质量通量均高于0.1 μm颗粒。主要原因是热泳力的大小与颗粒半径的一次方正相关，但颗粒质量与半径的三次方正相关，因此不管热泳力作用方向与重力方向是否同向，热泳力对于大粒径颗粒的相对影响均可忽略。

图7 考虑热泳力时壁面质量通量绝对差值沿轴向的分布Fig.7 Distribution of absolute difference of wall mass flux along axial direction considering thermophoresis force

由于热泳力的主要作用范围在温度边界层内，故可关注边界层厚度对于颗粒运动的影响。

温度边界层厚度表达式为：

(3)

式中：Rey为近壁面雷诺数；δT为温度边界层厚度；Prb为主流水普朗克数。

颗粒也会在近壁面形成浓度边界层，参照式(3)可得：

(4)

式中：δC为浓度边界层厚度；Scb为主流水施密特数。

联立式(3)和式(4)可知，浓度边界层厚度与温度边界层厚度的比值即相对厚度为：

(5)

图8给出了浓度边界层与温度边界层相对厚度的变化情况。从图8可以看出，粒径为0.1 μm和1.0 μm粒径颗粒表现出相似的波动，即在内壁温度达到跨临界温度Tpc时，δC/δT为极大值；当主流水温度等于Tpc时，δC/δT为极小值。造成这一现象的主要原因与温度边界层和浓度边界层在跨临界区附近的厚度变化有关。因为铁离子溶液总是优先在靠近壁面处氧化成核并形成颗粒，因此当边界层内流体还未达到跨临界温度时，流体湍流波动较弱，边界层形态较为稳定，此时浓度边界层厚度表现为沿轴向逐渐增加，同时温度边界层沿轴向增厚速率小于浓度边界层，导致在内壁温度达到跨临界温度时，δC/δT达到极大值。之后，由于近壁面流体进入临界区，物性参数剧烈波动，但主流水尚未达到临界态，因此在近壁面处湍流波动加剧，流体边界层厚度总体表现出减小趋势，同时流体导热系数下降，颗粒成核速率急剧上升，共同导致δC减小速度慢于δT，最终导致当主流水温度达到跨临界温度时，δC/δT达到极小值。随后，流体趋于稳定，湍流波动较临界区显著下降，δC/δT重新增大。

图8 浓度边界层与速度边界层相对厚度的变化Fig.8 Variation of the relative thickness of the concentration boundary layer and the velocity boundary layer

从已知条件出发，可通过降低工质水中的铁离子浓度，以期降低含铁粒子粒径。同时小粒径颗粒更容易受到外力因素的影响，可以考虑增加特殊的外力，如因为Fe3O4为磁性颗粒，可以利用磁场来部分抵消热泳力对颗粒运动的影响，同时增强颗粒指向壁面的力，以达到使颗粒集中沉积的目的。在检修管理层面，加以小范围的“点检定修”有利于超临界受热面服役可靠性的提高。

3 结 论

(1) Realizablek-ε模型适用于超临界水的湍流模拟，同时重力对于低热流密度下水平细管的超临界水流动影响不明显。

(2) 颗粒运动受流场和自身重力的双重影响，且颗粒尺寸差异导致颗粒与壁面的运动特点有明显差异。小粒径颗粒主要受流场作用，且与壁面的碰撞频率更高；大粒径颗粒主要受自身重力影响，这种特性有利于颗粒集中沉积。

(3) 热泳力对于小粒径颗粒的影响更为明显，这种影响可以通过温度边界层与浓度边界层的相对厚度变化反映，相对厚度与流体温度存在密切关系。