考虑灾民有限理性的应急物资调度研究

张志伟，朱昌锋*，王庆荣，张正坤，刘康儒

（1.兰州交通大学 交通运输学院，兰州 730070；2.兰州交通大学 电子与信息工程学院，兰州 730070）

近年来，随着突发事件频发，人民的生命财产遭受了巨大损失.因此突发事件后，在黄金救援时间内将应急物资运到受灾点是降低突发事件对社会造成严重损失的关键.

针对突发事件后应急物资调度问题，国内外学者站在完全理性的角度进行了大量研究.大多数学者主要通过构建单目标［1-3］和多目标［4-6］规划模型来解决该问题，也有少数学者通过建立双层规划［7-10］模型为决策者提供可行的应急物资调度方案.然而，面对突发事件，由于外界环境的复杂性及决策者认知的局限性，决策者很难做到完全理性.既有研究已经证实人在决策时并非完全理性，而是表现出有限理性的，存在参考依赖、风险偏好和损失规避等行为.因此，不少学者采用Kahneman等［11］提出的前景理论模型研究人的有限理性行为.曹庆奎等［12］通过考虑灾民感知满意度，引入前景理论，研究了应急人员调度问题.徐君翔等［13］通过考虑决策者的有限理性，引入累积前景理论，研究了应急物资调度路径选择问题.郑彦辉等［14］通过前景理论刻画应急物资分配的灾民心理满意度，研究了非合作博弈环境下的应急物资调度问题.但在应急环境不确定的情况下对前景理论的应用以及灾民对应急物资的运送时间满意度和分配满意度的研究较少.除此之外，大多数研究者在考虑应急物资需求量时忽略了突发事件后应急环境的不确定性.

鉴于此，本文通过考虑突发事件后应急环境的不确定性以及有限理性条件下灾民对应急物资的运到时间满意度和分配满意度，分别以最大化时间满意度的前景值和分配满意度的前景值为目标函数，构建应急物资多目标调度模型，并设计NSGA-Ⅱ算法求解该模型，以确保应急物资调度的时效性和公平性，提高灾民对应急物资调度结果的感知满意度.

1 数学模型

1.1 问题描述

假设某地发生突发事件，有m个物资供应点，物资供应点集合O=｛1，2，…，i，…，m｝．需要救援n个物资受灾点，受灾点集合D=｛1，2，…，j，…，n｝．dij表示从应急物资供应点i到需求点j的路径距离．tij表示从应急物资供应点i到需求点j的实际运输时间．cij表示应急物资供应点i分配给应急物资需求点j的物资量．Cj表示物资需求点j的物资需求量，Mi表示物资供应点i物资存储量．xij表示若应急物资供应点i对需求点j进行救援，则xij=1，否则xij=0．ωj为受灾点j的权重函数值为应急物资运输工具平均速度．

1．2 基于前景理论的灾民感知满意度刻画

前景理论价值函数体现了灾民在面临收益时是风险规避的，而在面临损失时是风险偏好的，并且，比起收益，灾民对损失更加敏感．其定义如下：

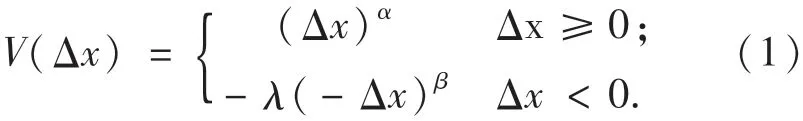
式中：α为收益敏感系数，且0＜α≤1；β为损失敏感系数，且0＜β≤1；λ为损失规避系数，且λ≥1；通常α，β取值为0．88，λ取值为2．25；Δx为实际值x相较于某一参照水平x0的偏离值．价值函数曲线如图1所示．

图1 价值函数曲线Fig．1 Value function curve

前景理论的权重函数反映了灾民往往会重视小概率事件而忽略中大概率事件，其定义如下：

当灾民获得收益时：

当灾民获得损失时：

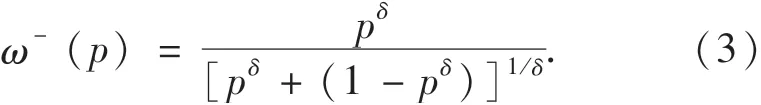
式中：ω+（p）为灾民获得收益时的权重函数；ω-（p）为灾民获得损失时的权重函数；p为事件发生的实际概率；γ为收益感知概率系数，取0．61；δ为损失感知概率系数，取0．69．权重函数曲线如图2所示．

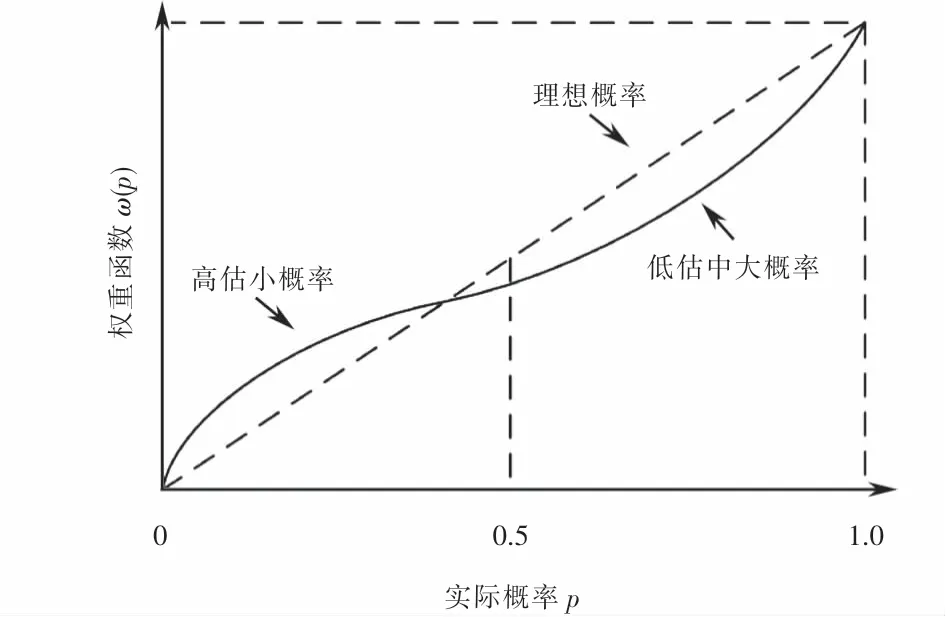
图2 权重函数曲线Fig．2 Weight function curve

1．2．1 时间满意度

应急物资送达时间越早对灾民而言是收益的，反之则为损失．用应急物资运到时间偏离程度表示的价值函数值来刻画灾民对运到时间的感知满意度．其中，用三角模糊数的模糊均值来刻画应急物资有效到达时间的参照点［15］，其中为模糊上界为模糊主值为模糊下界．w1，w2和w3分别代表三角模糊数上界、主值和下界的权重系数．三角模糊数的主值通常是最重要的属性，因此应该被给予较高的权重．上界和下界是边际约束，因此它们应该被给予较低的权重．基于此，w1和w3取1／6，w2取4／6．应急物资有效到达时间参照点定义为

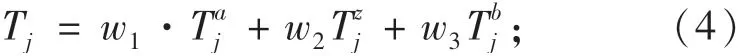
因此，对于物资需求点j来说，应急物资运到时间偏离度为

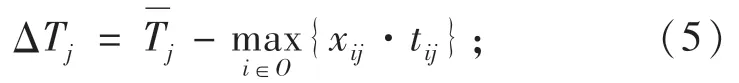
用价值函数刻画灾民对应急物资运到时间的感知满意度，即：

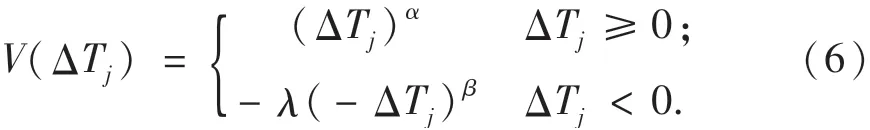
1．2．2 分配满意度

应急物资分配量越多对灾民而言是收益的，反之则为损失．用应急物资分配量偏离程度表示的价值函数值来刻画灾民对分配量的感知满意度．其中，用三角模糊数的模糊均值Uj来刻画应急物资有效分配量的参照点，其中为模糊上界模糊主值为模糊下界．应急物资有效分配量参照点定义为

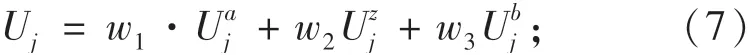
因此，对于物资需求点j来说，应急物资分配量偏离度定义为

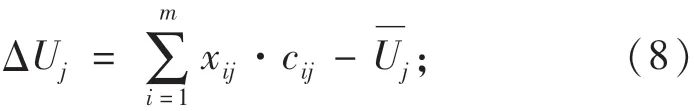
用价值函数衡量灾民对应急物资分配量的感知满意度，即：

构建数学模型如下：

约束条件

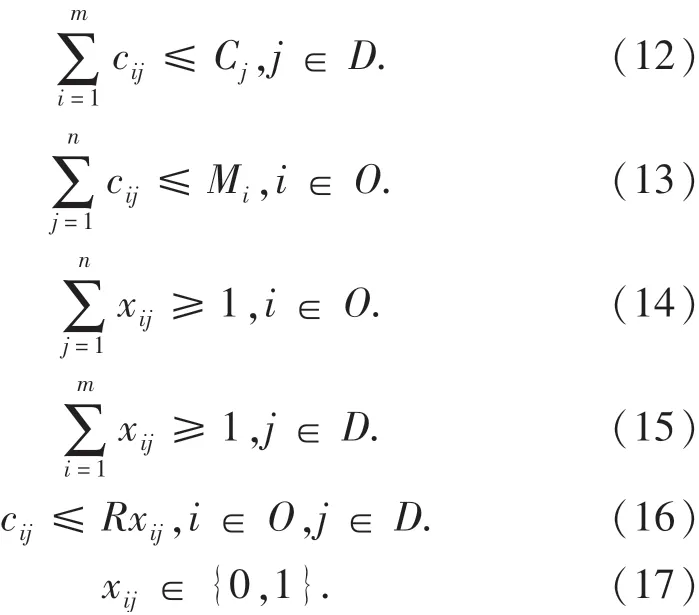
式（10）为最大化灾民对应急物资运到时间的感知满意度．式（11）为最大化灾民对应急物资分配量的感知满意度．式（12）表示应急物资供不应求．式（13）表示每个物资供应点调运到各个受灾点的物资总量不能超过其自身存储量．式（14）保证每个物资供应点都参与到应急救援过程中．式（15）保证对每一个受灾点都被进行救援．式（16）保证cij值与xij值的一致性，其中R为惩罚系数，为充分大的正数．式（17）表示决策变量xij为0-1变量．

2 算法设计

本文所建模型是多目标规划问题，采用第二代非支配排序遗传算法［16］（non-dominated sorting genetic algorithms-II，NSGA-II）求解考虑灾民有限理性的应急物资调度模型.根据模型特点，选择0-1编码，染色体编码如图3所示.

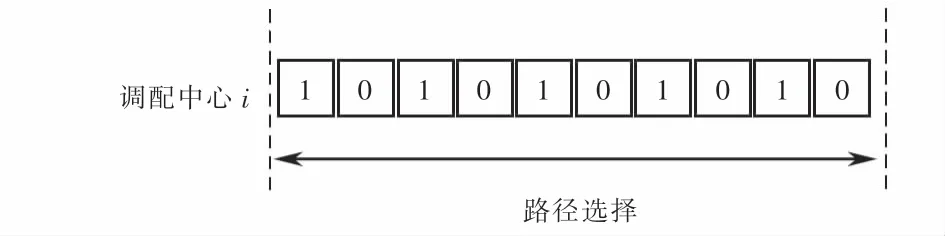
图3 编码示例Fig．3 Coding example

从左至右依次表示调配中心i是否对各受灾点进行物资调配径路选择，如选择路径则分配物资，否则不分配物资.算法关键步骤如下：

1）选择操作

本文采用二元锦标赛方法选择子代种群，保证较大概率选择最优个体和淘汰最差的个体，在一定程度上避免产生过早收敛现象.

2）交叉操作

为保持种群多样化，提高Pareto最优解集质量，对染色体进行两点交叉，如图4所示.

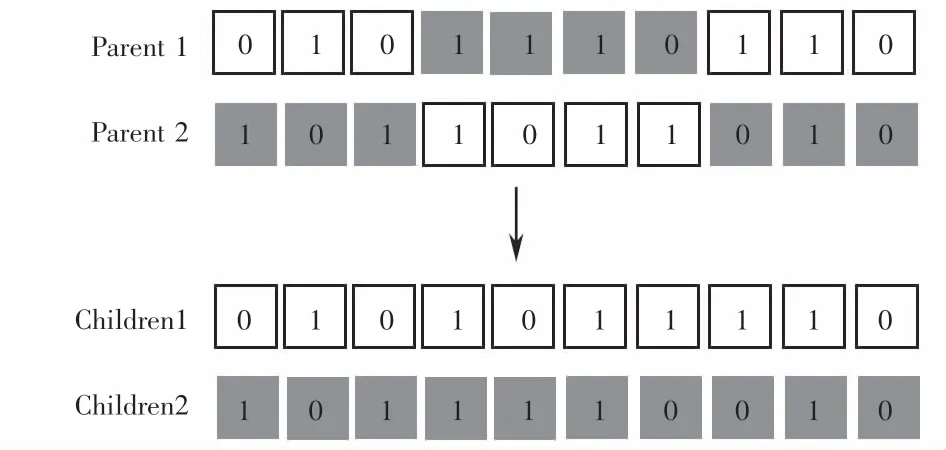
图4 交叉示例Fig．4 Cross example

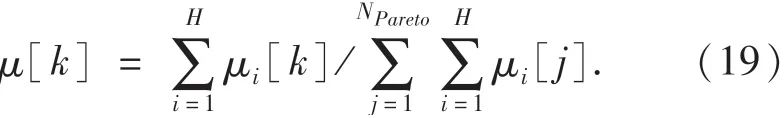
然后计算Pareto解集中每个候选解在整个目标空间的得分：

3）变异操作

本文采用两点变异的方法，对染色体两点之间染色体片段进行变异操作，如图5所示.

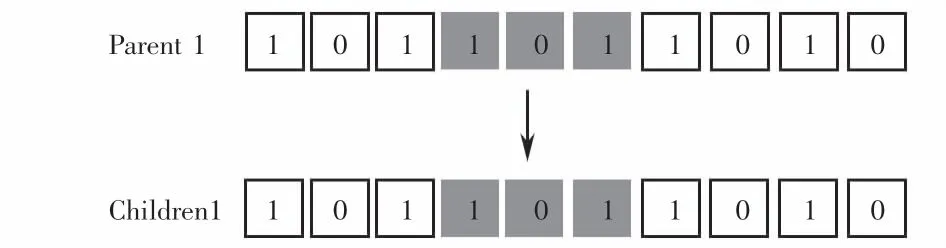
图5 变异示例Fig．5 Variation example

4）最终解的筛选

本文采用模糊逻辑法来从最优解集中筛选最佳折中解，首先计算Pareto解集中每个候选解在每个目标空间的得分：

式中：H为优化目标的数量；NPareto为Pareto解集的数量；μ［k］值最大的候选解就是最佳折中解．

基于上述分析，本文算法步骤如下：

Step1：随机生成大小为Popsize的种群Pt，t=1，选择应急路径并分配应急物资；

Step2：通过选择、交叉、变异等操作，产生子代种群Qt；

Step3：合并父代与子代种群，令Rt=Pt∪Qt；

Step4：利用快速非支配排序法对Rt进行非支配排序形成非劣解集；

Step5：按照非支配序从小到大，逐层选取染色体进入下一代Pt+1，直到染色体数目为Popsize；

Step6：令t=t+1，判断是否满足迭代终止条件，若满足，算法结束，否则，通过选择、交叉、变异等操作，产生子代种群Qt+1，转到Step3；

算法流程如图6所示.

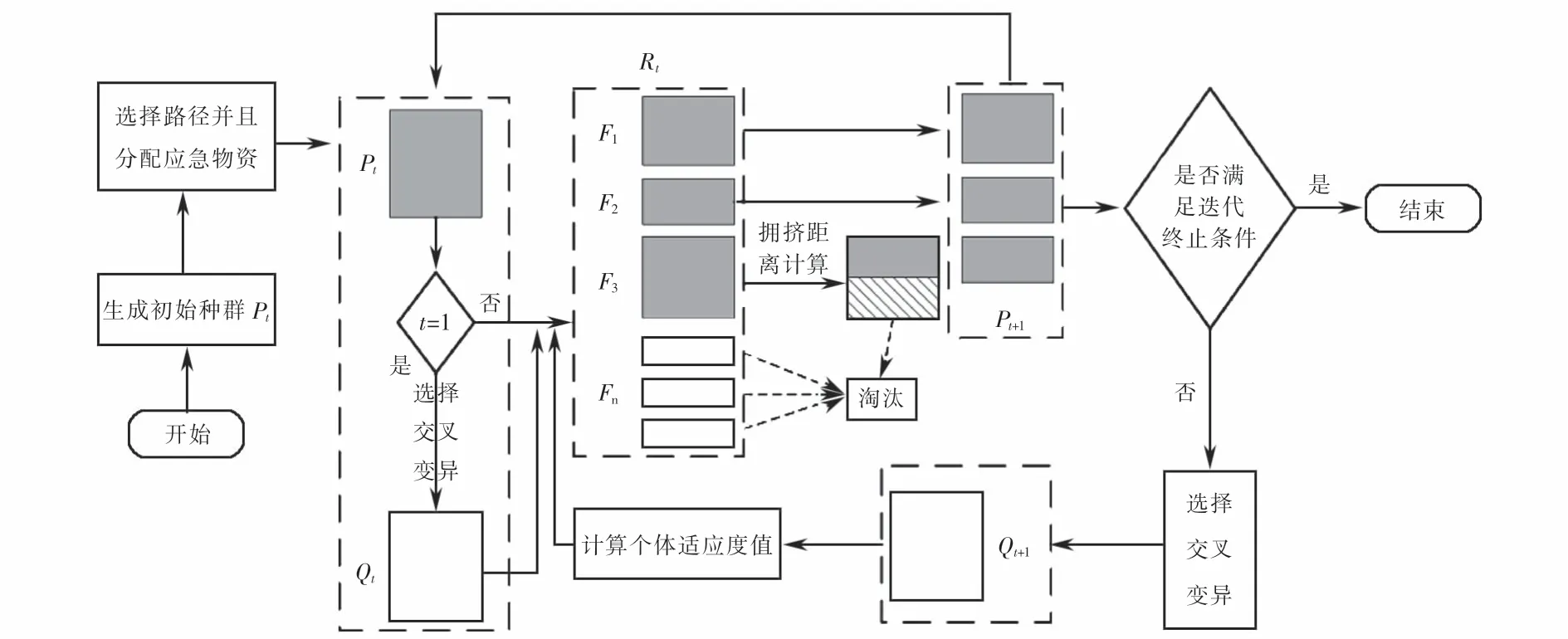
图6 算法流程Fig．6 Algorithm flow

3 算例分析

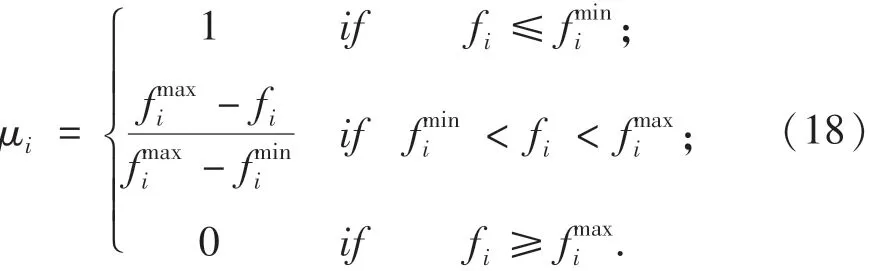
3.1 算例背景

假设某地发生重大突发事件，受灾点数n=10，编号1～10；调配中心数m=5，编号1～5．应急物资运输网络如图7所示．调配中心与受灾点的路径距离dij如表1所列，根据调配中心至受灾点间的路径距离和应急物资运输工具的平均速度v-可得出物资最短运输时间tij.各调配中心应急物资存储量如表2所列，各受灾点间的需求量如表3所列.

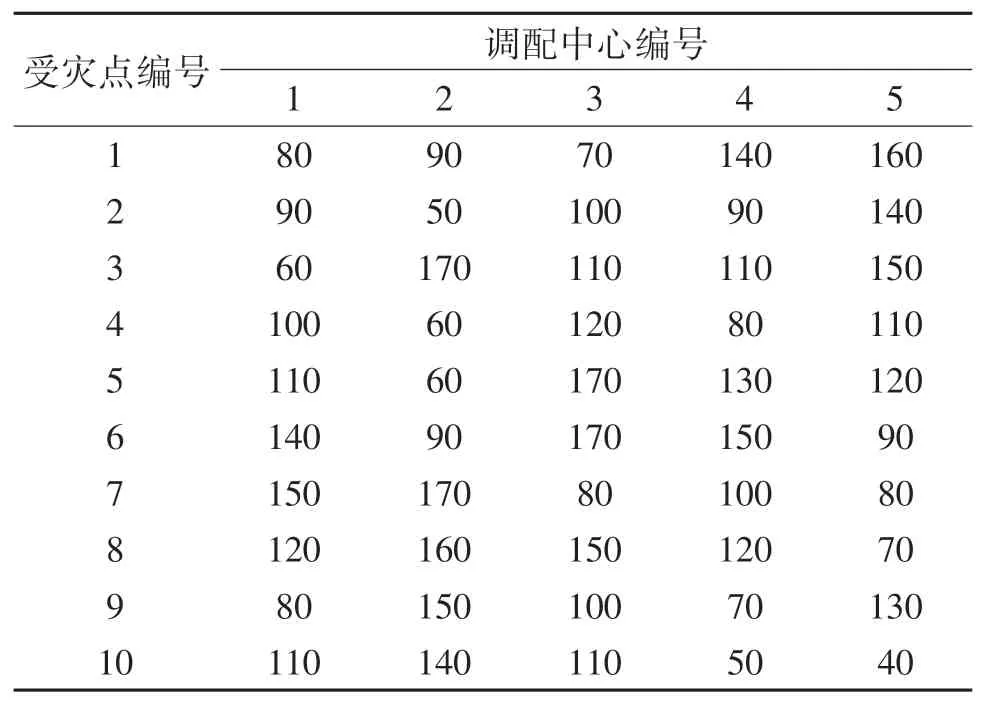
表1 路径距离Tab．1 Path distance km

表2 物资存储量Tab．2 Storage capacity of emergency materials kg

表3 受灾点物资需求量Tab．3 Material demand of disaster points kg

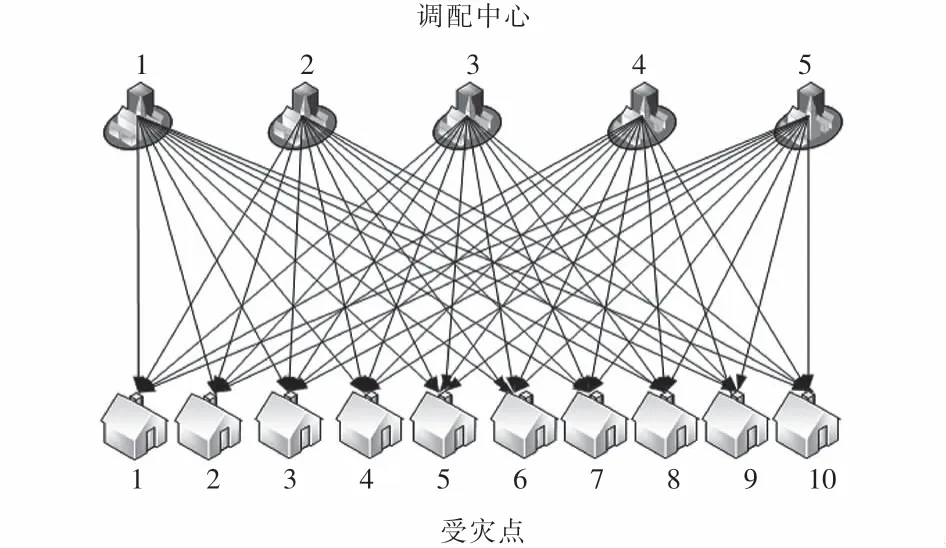
图7 应急物资运输网络Fig．7 Transport network of emergency materials

3.2 结果分析

设置种群规模为100，交叉概率为0.75，变异概率为0.2，基于VisualStudio2017开发环境C++语言和Matlab语言实现本文的算法.本文利用帕累托一级前沿解的个数和两个目标函数值的稳定性来判断算法的收敛性能.结果如图8～9所示.

图8为帕累托一级前沿解数量随着迭代次数的变化情况，从图8中我们可以发现帕累托一级前沿解的数量在达到6之后趋于稳定，因此可以说明本文设计的算法是有效的.

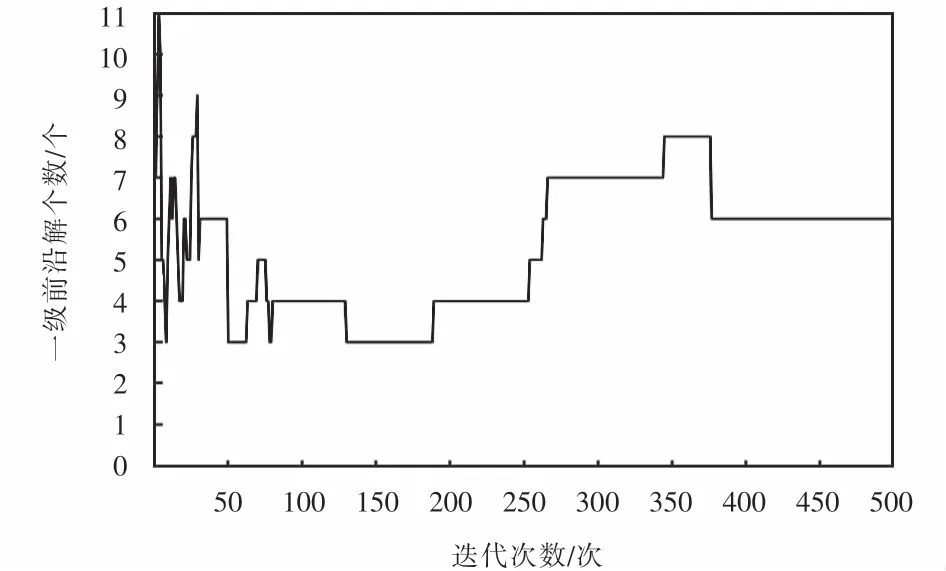
图8 帕累托一级前沿解个数Fig．8 Number of Pareto first-order fronts

图9为应急物资运到时间满意度前景值和应急物资分配满意度前景值随着迭代次数的变化情况，可以发现时间满意度前景值在迭代次数为25左右时收敛，分配满意度前景值在迭代次数为250左右时收敛.因此进一步说明了算法的收敛性能是良好的.

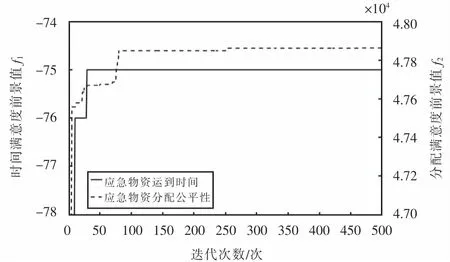
图9 算法迭代图Fig．9 Algorithm iteration diagram

求得的最优种群如图10所示.

从图10可以发现灾民对应急物资运到时间表现为损失心理，而对应急物资分配公平性表现为收益心理.

图10 最优种群Fig．10 Optimal population

从最优种群中筛选出五级前沿解，结果如图11所示.由于本文以最大化灾民对应急物资运到时间的感知满意度前景值和分配满意度前景值为目标函数，所以帕累托前沿呈上“凸”形状.图11显示：每一级帕累托前沿非支配解均匀分布在解空间中，且对立特性描述准确.

在图11中一级前沿解6个帕累托点.每个帕累托点对应一种应急物资调度方案，每个方案对应的目标值函数值如表4所列.

图11 帕累托前沿Fig．11 Pareto front

从表4可以看出一级帕累托前沿有6个帕累托点，其对应的应急物资运输时间满意度前景值都小于0，说明在应急物资运到时间上总体上是有略微损失的，而应急物资分配满意度前景值都大于0，说明在应急物资供不应求的情况下，合理分配应急物资，灾民表现出的心理感知是收益的.应急物资分配结果如图12所示.

表4 应急物资调度方案下的目标值Tab．4 Target values under the emergency materials scheduling scheme

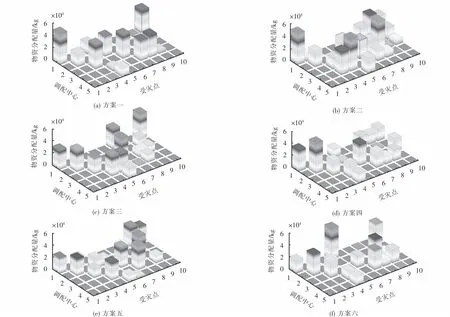
图12 一级前沿解应急物资调度结果Fig．12 Scheduling results of first-level frontier solution emergency materials

本文采用模糊逻辑法从帕累托一级前沿中找到应急物资调度最优方案为方案1，如图12（a）所示.可以发现每个调配中心都参与了应急救援任务，且每个受灾点都被分配应急物资，这在一定程度上保证了应急救援的公平性.除此之外，方案一所对应的各受灾点的应急物资运输时间满足程度如图13所示.

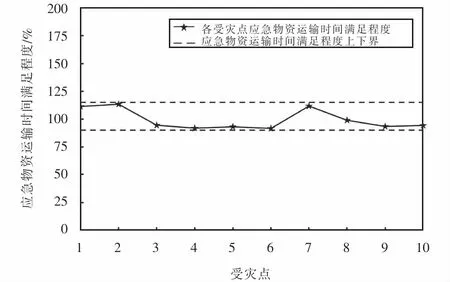
图13 应急物资运输时间满足程度Fig．13 Satisfaction degree of transportation time for emergency materials

从图13可以看出，各受灾点应急物资运输时间满足程度都在［90%，115%］之间，应急物资运到时间正负偏差最大为15%，因此对于各受灾点而言，方案1下的应急物资运输时间也是相对公平的，既不存在某一受灾点应急物资早到，也不存在另一受灾点应急物资严重迟到的现象.因此，这也在一定程度上保证了应急救援的公平性.

3.3 参数分析

由于应急物资调度是处于开放环境下的，且决策者是有限理性的，考虑到价值敏感系数α，β以及权重系数γ，δ对综合前景值的影响，有必要对其进行灵敏度分析．分析结果如图14～17所示．

图14 价值敏感系数对时间满意度的影响Fig．14 Influence of value sensitivity coefficient on time satisfaction

1）α和β

从图14，可以发现收益敏感系数α对时间满意度前景值并没有很大的影响，然而随着损失敏感系数β的增加，时间满意度前景值增大，一直增加到-10，但并没有超过0.说明应急物资到达时间对于灾民而言是损失的.应该引起决策者的高度关注.

从图15可以看出，损失系数β对分配满意度前景值并没有影响，但是收益敏感系数α对分配满意度前景值的影响很大．可以从图15发现当时对分配满意度前景值并无很大的影响，然而当时分配满意度前景值随着α值的增大而骤增．此外，可以发现物资分配满意度前景值恒大于0，说明在应急物资供不应求的情况下，合理分配有限物资，灾民心理感知是收益的．

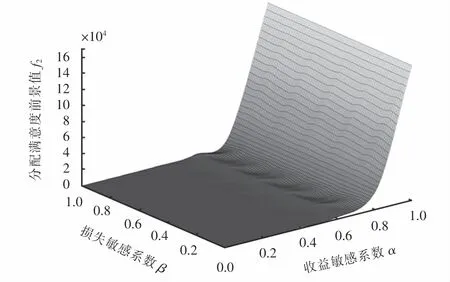
图15 价值敏感系数对分配满意度的影响Fig．15 Influence of value sensitivity coefficient on distribution satisfaction

2）γ和δ

从图16可以看出，时间满意度前景值被收益感知概率系数γ和损失感知概率系数δ所影响，随着收益感知概率系数γ的增加，时间满意度前景值在上下波动．波动幅度为［-50，+50］，随着损失感知概率系数δ的增加，时间满意度前景值基本呈线性增加.

图16 权重系数对时间满意度的影响Fig．16 Influence of weight coefficient on time satisfaction

从图17可以看出，损失感知概率系数δ值对分配满意度前景值并没有太大影响，但是收益感知概率系数γ对分配满意度前景值有很大的影响，随着收益感知概率系数γ值的增加，分配满意度前景值总体上呈线性增加.

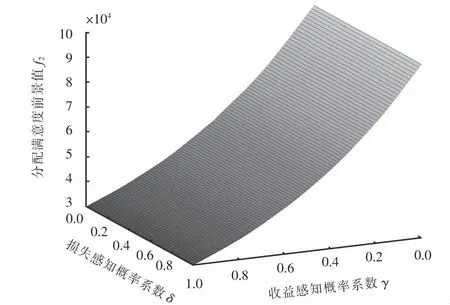
图17 权重系数对分配满意度的影响Fig．17 Influence of weight coefficient on distribution satisfaction

4 结论

本文通过考虑灾民的有限理性行为，基于应急物资调度优化问题，建立了多目标优化模型，并设计NSGA-II算法求解该模型，从求得的Pareto最优解集中选取最优解作为模型的满意方案.仿真结果表明：

1）考虑灾民感知满意度的多目标优化模型有更优的收敛性.

2）用前景理论刻画灾民感知满意度能很好地反映灾民对应急救援的实际心理感知.

3）设计NSGA-II算法获得的Pareto解集具有更高的可行性与有效性.考虑到次生灾害对应急救援过程的影响，如何把次生灾害考虑到模型中将是下一步研究的重点.