钢筋混凝土空心板桥预制梁水化热分析研究

唐 杨， 王国炜， 王大为

(1.五峰土家族自治县农村公路管理所，湖北 宜昌 443413；2.济南金衢公路勘察设计研究有限公司，山东 济南 250101；3.温州市交通规划设计研究院，浙江 温州 325000)

0 引言

空心板梁桥是中、小跨径桥梁常见的结构形式，目前针对空心板梁桥的研究主要集中在结构设计[1]、结构受力[2]、理论计算方法[3]、病害加固[4]和施工新技术[5]等方面。

由于空心板梁板结构不具有大体积混凝土结构厚度大、一次性混凝土浇筑量大的特点，因而目前关于空心板梁板结构的水化热研究较少。相关文献资料表明，姚杰[6]通过研究空心板的早期裂缝，对其出现早期裂缝的内部原因和外部原因进行详细剖析，结果表明水泥的水化热就是空心板出现早期裂缝的主要内部原因之一；张鹏程等[7]针对连续厚板，在内部均匀设置空腔，分析了空心板的温度场和应力场，研究表明空腔可以改善内部传热环境、控制内部温升和减小温度应力；刘国波[8]通过分析预制预应力空心板梁常见的质量通病后认为：施工环境温度是造成空心板开裂的重要原因之一。综合来看，针对空心板结构的水化热研究大都集中在定性分析上，缺乏针对具体工程案例的定量分析，同时在实际施工中尚未引起工程技术人员的足够重视。

以一片钢筋混凝土空心板预制梁为例，对其温度场和应力场进行计算分析，可为空心板预制梁的施工期养护提供理论参考。

1 工程概况

某上承式钢筋混凝土箱型拱桥的拱上建筑采用11.2 m跨径的C40装配式空心板简支梁结构，其中空心板预制中梁的截面尺寸如图1所示，预制梁的梁高0.6 m，顶板宽1.39 m，底板宽1.49 m，顶板与底板的厚度均为0.08 m，空心板的空心截面形状为圆形，直径为0.44 m。

图1 空心板预制中梁截面尺寸(单位: mm)

空心板预制前首先需要整平场地、浇筑混凝土台座，混凝土台座浇筑采用C25混凝土，再于混凝土台座上铺设3 cm厚的钢板作为底模，端模和侧模均采用1 cm厚钢板，内模采用3.2 mm厚度的固定气囊，固定气囊是采用橡胶和纤维织物结合硫化而成[8-10]。

2 分析理论

2.1 热传导微分方程

混凝土结构在实际工作条件下的热传导微分方程[11]

(1)

式中,T为温度场，表示温度在时间域和空间域的分布；t为时间;λ为导热系数;cp为质量定压热容;ρ为密度;θ为绝热温升;x、y、z为空间域的3个坐标方向。

2.2 初始条件

大多数情况下，初始时刻的温度场可以视为一个常量，初始条件为

T(x,y,z,0)=C

(2)

式中,T为温度场;C为常量。

2.3 边界条件

边界条件通常有4类[12]。

第1类边界条件为边界温度是时间的已知函数，数学表达式为

T=f(t)

(3)

式中,T为温度场;f(t)为时间的函数。

第2类边界条件为物体表面的热流量是时间的函数，数学表达式为

(4)

式中,λ为导热系数;n为表面外法线方向。

第3类边界条件为已知物体表面对流热交换情况，数学表达式为

(5)

式中,β为表面热交换系数;T为物体表面温度;Ta为环境温度。

第4类边界条件为2种固体接触良好，则接触面上的温度和热流量都是连续的，数学表达式为

(6)

式中,T1、T2分别为2种接触良好固体的温度。

3 关键分析参数确定

3.1 绝热温升

混凝土结构不与外界发生任何热交换，将混凝土的水化热全部转化为混凝土的温度值，称为绝热温升[13]，计算为

(7)

式中,T(t)为混凝土龄期为t时的绝热温升；W为单位体积混凝土的胶凝材料用量；Q为单位质量胶凝材料的水化热总量；C为混凝土的比热容；ρ为混凝土的密度；t为混凝土龄期；m为常数，随水泥品种、比表面积及浇筑温度的不同而不同。

3.2 传热系数

根据混凝土表面采用不同的保温材料，其传热系数为[14]

(8)

式中,β为保温层的热传系数；βq为空气层的热传系数，取23 W/(m2·℃)；λi为各保温层材料的导热系数；δi为各保温层材料的厚度。

3.3 混凝土弹性模量

根据文献[15]规定，混凝土的弹性模量为

E(t)=kE0(1-e-ctb)

(9)

式中,E(t)为龄期t时的弹性模量；t为计算混凝土龄期；k为混凝土中掺合料对弹性模量的修正系数；E0为混凝土最终弹性模量，一般近似取标准养护条件下28 d龄期的弹性模量；c为系数，应通过试验确定，无试验数据时可近似取0.4；b为系数，应通过试验确定，无试验数据时可近似取0.6。

3.4 混凝土抗拉强度

文献[13]表明，混凝土的轴心抗拉强度在一定情况下是混凝土的真实抗拉强度，控制混凝土开裂应以轴向抗拉强度为依据，混凝土的轴心抗拉强度标准值为

ftk(t)=ftk(1-e-γt)

(10)

式中,ftk(t)为t龄期的轴心抗拉强度;ftk为28 d龄期的轴心抗拉强度标准值；γ为系数，应通过试验确定，无试验数据时可近似取0.3。

3.5 环境温度

环境温度通常采用正弦函数和常数函数拟合。当昼夜温差较为显著时，采用正弦函数拟合环境温度的变化，正弦拟合函数为[16]

(11)

式中,F(t)为环境温度；t为时间;t0为迟延时间；T为环境温度变化幅度;T0为平均温度。

当环境温度变化幅度不大时，可简化为常数函数近似模拟环境温度。

3.6 抗裂性能评价

文献 [13]表明，混凝土的抗裂性能判断

(12)

式中,λ为掺合料对混凝土抗拉强度的影响系数;ftk(t)为t龄期的轴心抗拉强度标准值;K为混凝土抗裂安全系数，通常取1.15。

4 模型建立

空心板预制梁的水化热分析采用Midas FEA NX有限元分析软件，该程序在水化热分析领域具有较为广泛的应用。

为了节约计算资源，由于各种边界条件和荷载的对称性，具体建模时仅仅建立1/4模型。建模时除了建立预制梁、钢板、混凝土台座的几何模型外，考虑四周一定范围内土体的传热，材料的属性参数见表1。在几何模型建立中，将1/4模型的土体几何大小设置为(1.49×6.325×1.0)m。几何模型采用自由网格划分技术划分网格，有限元模型如图2所示。

图2 有限元模型

表1 材料参数表

在计算分析中，考虑预制梁混凝土的收缩徐变，根据文献[17]设置以下计算参数：28 d龄期的立方体抗压强度为40 MPa，开始收缩时的混凝土龄期为3 d，周围环境的相对湿度为70%，由于采用一般的硅酸盐水泥，故而将水泥系数设置为5。

在边界上，施加2个方向的对称边界条件，同时施加土体底部固结和土体四周边界的法向支撑。在荷载上，考虑热源、固定温度和对流。由于空心板预制梁浇筑时混凝土台座已经浇筑较长时间，其温度已经趋于稳定，热源荷载仅仅考虑预制梁部分。热源根据预制梁C40混凝土的配合比：水∶水泥∶砂∶石=0.41∶1∶1.086∶2.310，换算得到单位体积混凝土中42.5级水泥用量为513 kg，查得42.5级水泥的最终水化热为377 kJ/kg，根据式(7)计算得到最大绝热温升为80.58 ℃，m根据入仓温度15 ℃取0.34，从而得到完整的热源函数，混凝土的绝热温升随龄期的变化规律如图3所示。

图3 预制梁混凝土的绝热温升

对流系数采用式(8)进行计算，根据钢材的热传系数58 W/(m2·℃)计算得到端模和侧模位置的对流系数为22.9 W/(m2·℃)；由于空心板预制梁顶面浇筑后暂时直接与空气接触，计算得到对流系数为23 W/(m2·℃)，周边土的顶面同样与空气直接接触，故而设定相同的对流系数；参照与固定气囊的材料较一致的各种橡胶制品的导热系数，将固定气囊的导热系数确定为0.18 W/(m2·℃)，计算得到与固定气囊接触的空心板内腔的对流系数为0.13 W/(m2·℃)。

由于空心板混凝土中不加入掺合料，查询得到混凝土弹性模量的修正系数β=1，根据式(9)取b、c的近似值，得到预制梁混凝土的弹性模量随龄期的变化规律如图4所示。由式(10)得到预制梁混凝土的抗拉强度随龄期的变化规律如图5所示。

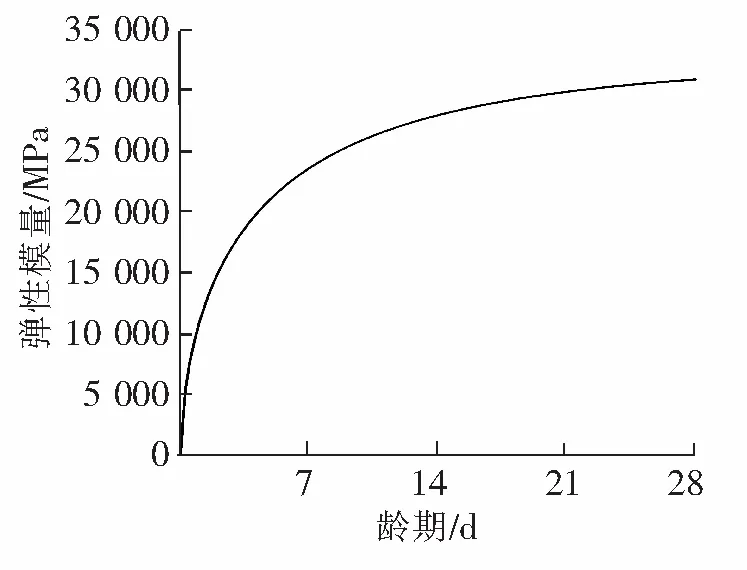
图4 预制梁混凝土的弹性模量

图5 预制梁混凝土的抗拉强度

周边土的底面和四周不考虑温度的变化，设定为固定温度18 ℃。在环境温度的设置上，根据近期的天气预报和计划浇筑时间计算得到环境平均温度为20 ℃，环境温度变化幅度为9 ℃，迟延时间为0，从而得到环境温度随龄期的变化规律如图6所示。

图6 环境温度随龄期的变化

计算分析时间段设置为预制梁混凝土浇筑完成后28 d时间，收敛判断准则设置为位移与内力双控。由于预制梁混凝土拌合时采用预冷骨料、加冰等办法[13]控制混凝土的初始温度，在计算中将初始温度设置为15 ℃。

5 计算结果分析

通过计算，提取28 d内各龄期预制梁的温度变化情况和第一主应力变化情况，预制梁的最高温度与最低温度变化情况如图7所示；通过与C40混凝土相应龄期的抗拉强度对比，预制梁的拉应力最大值变化情况如图8所示。

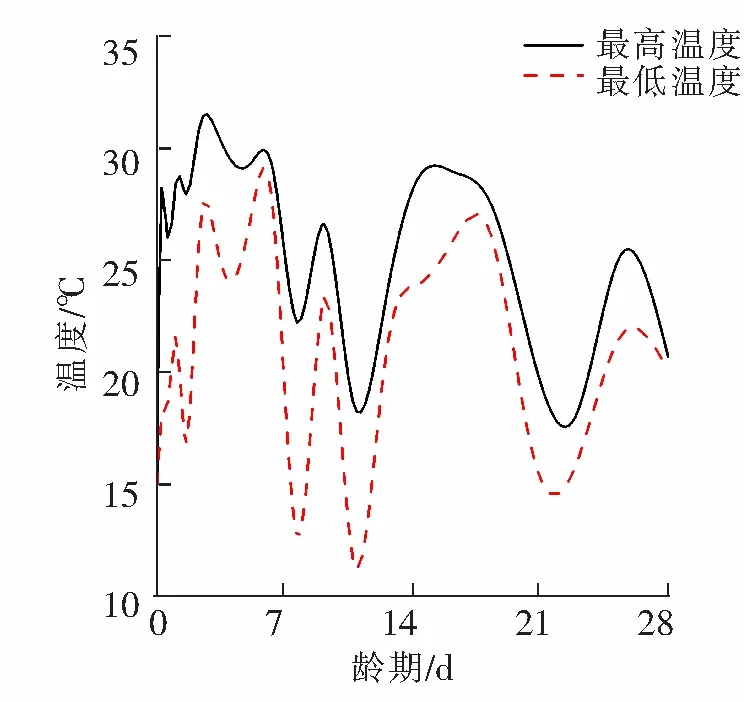
图7 预制梁温度变化曲线

图8 预制梁温度应力最大值变化曲线

由图7可见：预制梁的最高温度为31 ℃，出现在3.1 d附近；最大温差为11.1 ℃，出现在1.59 d附近。由此可见，预制梁在养生阶段未采用温控措施时，环境温度对预制梁的温度场影响较大。

由图8可见：预制梁在28 d内的温度应力存在较多时段超过其混凝土的抗拉强度，其主要时段为0～2 d、7～8 d以及10.5～11 d；预制梁的温度应力最大值出现在7～8 d时间段，达到3.64 MPa，远超预制梁此时的抗拉强度，发生开裂风险极大。

针对以上情况，对预制梁采取相应温控措施，具体措施如下：在侧模和端模表面粘贴5 cm厚的挤塑聚苯保温板，在预制梁的顶面覆盖4 cm厚的岩棉。相关资料表明挤塑聚苯保温板的导热系数为0.028 W/(m2·℃)、岩棉的导热系数为0.04 W/(m2·℃)，根据式(8)计算得到侧模和端模表面的对流系数为0.55 W/(m2·℃)，预制梁顶面的对流系数为1.26 W/(m2·℃)。

通过计算分析，得到预制梁的最高温度与最低温度变化情况如图9所示，拉应力最大值变化情况如图10所示，与之对应的预制梁抗裂情况如图11所示。

图9 温控后预制梁温度变化曲线

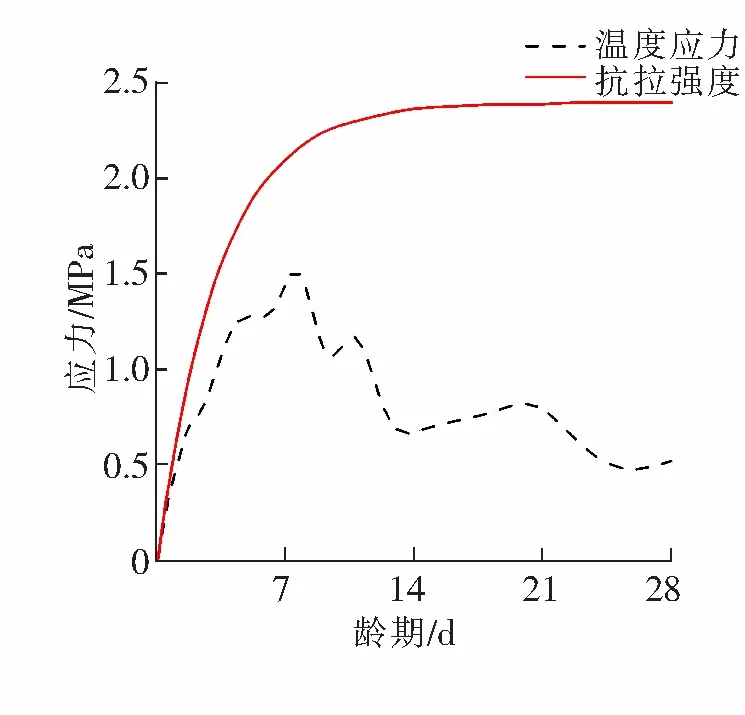
图10 温控后预制梁温度应力最大值变化曲线

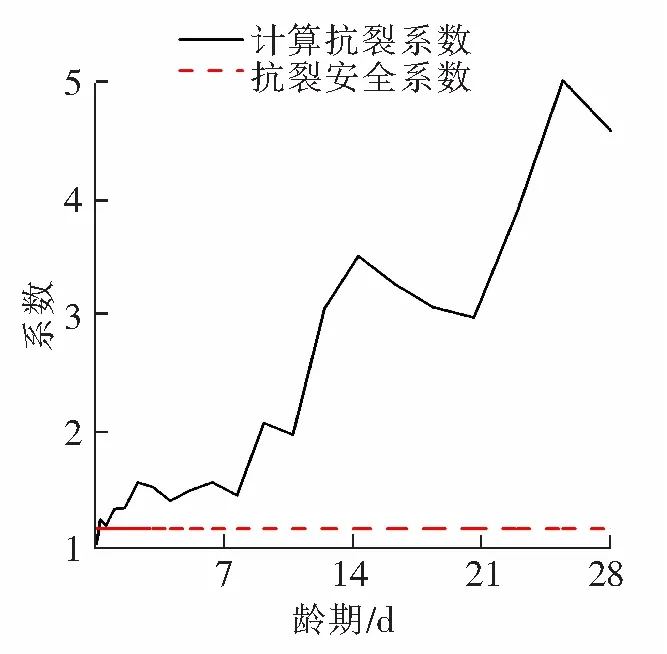
图11 预制梁抗裂系数

由图9可见：预制梁的最高温度为42.82 ℃，仍旧出现在3.1 d附近；最大温差为13.06 ℃，出现在2.29 d附近。从预制梁温度变化的总体趋势上看，在采取温控措施后，预制梁的温度变化波动减少，结构温度在3 d附近达到最大值后，温度总体呈现下降趋势。

由图10可见：采取温控措施后，28 d龄期内预制梁的拉应力均控制在C40混凝土的抗拉强度范围以内；预制梁的温度应力总体上呈现先增大后减小的变化趋势；在养生阶段的初期， 0～1 d时间段，预制梁的温度应力与抗拉强度较为接近；在1～7.68 d时间段，预制梁的温度应力与抗拉强度开始缓慢拉开距离；7.68 d以后，温度应力呈下降趋势，预制梁的抗拉强度仍在不断上升。

由图11可见：在整个28 d龄期内，仅仅在0～0.25 d时间段的计算抗裂系数(接近于1且大于1)低于抗裂安全系数1.15，0.25～9 d时间段的计算抗裂系数处于较低状态(小于2)，龄期在9 d之后，计算抗裂系数整体呈现上升趋势。

6 结论

通过对空心板预制梁的水化热分析，可以得到以下结论：

(1)由于环境温度变化幅度较大，在空心板养生期间应采取相应保温措施，避免空心板预制梁温度应力过大造成混凝土开裂。

(2)采取相应保温措施后，空心板预制梁的温度受环境温度的影响变小，温度应力可以有效控制在混凝土的抗拉强度以内。

(3)空心板预制梁0.25 d以前的计算抗裂系数低于抗裂安全系数，其开裂风险仍然较大，此时除了加强保温措施以外还应当加强环境温度的监测，建议在预算充足的情况下采取措施控制环境温度的变化。

(4)空心板预制梁的板厚较小，混凝土内部的温度上升程度有限，当环境温度波动较大且保温措施不完善的情况仍然可能产生不容忽视的拉应力，需要引起更多工程技术人员的重视。