宽高比对扁平箱梁气动力特性的影响规律及流场机理研究

范佳豪, 刘慧杰, 姜会民, 刘小兵,2,3, 杨 群,2,3

(1. 石家庄铁道大学 土木工程学院，河北 石家庄 050043；2. 河北省风工程和风能利用工程技术创新中心，河北 石家庄 050043；3. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043)

0 引言

现代的桥梁不断向着大跨和轻柔的方向发展，对风荷载愈发敏感[1-2]。扁平箱梁由于具有横向抗弯、抗扭性能好及良好的颤振稳定性[3-5]等优点，被广泛地应用于实际工程中，如国内建设的江东大桥[6]、青岛海湾大桥[7]，主梁都采用了扁平箱梁。掌握扁平箱梁的气动力特性及其发生机理对于扁平箱梁桥的抗风设计及气动优化[8-9]具有重要的参考价值。

已有学者对扁平箱梁进行了一些研究。其中李永乐等[10]以琼州海峡为背景，通过数值模拟对其主跨为3 500 m的超大跨度悬索桥中的扁平单箱梁进行了气动力特性的研究。研究结果发现,扁平单箱梁的三分力系数绝对值随风攻角增大而增大，较大风攻角下的扁平单箱梁稳定性能降低；而扁平箱梁的斯托罗哈数较小，表明该主梁型式具有较为良好的涡振性能。祝志文等[11]以丹麦大带东桥主跨加劲梁为研究对象，对不同风攻角下的扁平箱梁进行了二维数值计算，并将二维和三维主梁的整体气动力特性、表面压力分布进行对比。结果发现，在典型风攻角下扁平箱梁具有单一斯托罗哈数，且均大于成桥的状态。杨阳等[12]以寸滩长江大桥主桥的加劲梁为研究对象，采用风洞试验和数值模拟相结合的方法对扁平钢箱梁的气动力特性和涡振性能进行了研究。结果表明，该宽体扁平钢箱梁在不同风速下的静力三分力系数十分接近，受雷诺数的影响较小，该梁对风攻角变化比较敏感。李春光等[13]通过节段模型试验的方法，研究了宽高比为11.08的扁平钢箱梁在不同条件下对其气动力特性的影响。研究结果发现，随着风攻角由负变正，扁平钢箱梁断面的扭转气动力特性偏于不安全，而且在悬挑臂导流板以及底板设竖直中央稳定板不适于提高扁平钢箱梁断面的气动力特性。

从国内外学者的研究中可以发现，当前的研究多以某一工程实例为背景展开，其中研究的扁平箱梁的宽高比多为某一固定值。然而，随着交通量的日益增长，桥面逐渐向着更宽幅的方向发展，当前研究尚不能预测更宽幅扁平箱梁的气动力特性。因此，需要对扁平箱梁进行更为系统的研究，揭示截面宽高比对扁平箱梁气动力特性的影响规律，以更好地指导实际工程。以某跨海大桥初步设计方案为工程背景，通过CFD数值模拟的方法研究了4种不同宽高比扁平箱梁在7个风攻角下的气动力特性，并对其发生机理进行了分析。

1 数值计算方法与计算模型

1.1 数值计算方法

在流体力学中通过动量方程、连续性方程和能量方程来体现3个最基本的守恒定律(动量守恒定律、质量守恒定律及能量守恒定律)。其中不可压缩流动的连续性方程、动量守恒方程及能量方程分别为

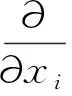
(1)

(2)

(3)

式中，ρ为静压；τij为应力张量；gi、Fi分别为i方向上的重力体积力和外部体积力。

数值计算方法采用雷诺平均法。CFD数值分析中，合理选取湍流模型是准确模拟箱梁断面周边流场的基本前提[14]。SSTk-ω湍流模型综合了标准k-ε模型和k-ω模型各自的优缺点，使得SSTk-ω湍流模型能获得优于标准k-ε模型和k-ω模型的模拟结果。通常认为SSTk-ω湍流模型是RANS模型中求解表现较好的湍流模型之一，比较适合于流动分离区的求解[15]。所以数值计算模型采用SSTk-ω湍流模型。

1.2 数值计算模型

以某跨海大桥初步设计方案为工程背景，扁平箱梁节段模型尺寸如图1所示，扁平箱梁模型宽度B=370 mm，高度H=64 mm，风攻角选用-6°～6°，风攻角方向沿风向斜向上为正，风速采用6 m/s。此扁平箱梁的宽高比为B/H=5.78，为了进一步研究不同宽高比对扁平箱梁气动效应的影响，增加B/H=5.0、8.0、10.0 3个不同宽高比的扁平箱梁，然后对4个不同宽高比的扁平箱梁进行数值模拟计算。对于扁平箱梁的二维数值计算，首先应确定它的边界条件和计算域，计算域选用矩形域进行计算，速度入口设置为velocity-inlet，出口设置为outflow，上、下边界为symmetry，因对称边界距箱梁模型中心的尺寸、速度入口边界对计算网格数量影响不大，故查阅文献[16]、文献[17]后将其确定为10B。经过试算后可知，当尾流区长度大于20B时，计算结果不再发生变化，故尾流区长度确定为20B。图2为扁平箱梁的计算域和边界条件示意图。通过试算当首层网格厚度为0.03 mm时可以保证无量纲Y+在1.0左右，故设置首层网格尺寸为0.03 mm。图3给出了B/H=5.78扁平箱梁的局部网格示意图。

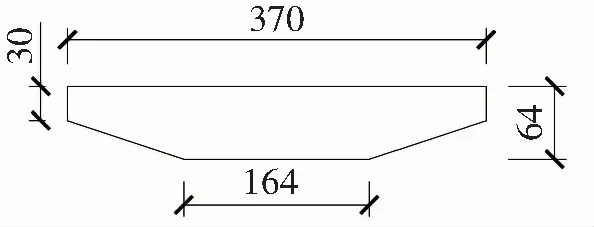
图1 节段模型尺寸图(单位：mm)

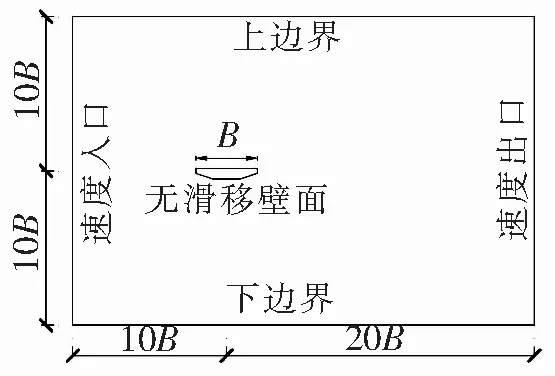
图2 计算域和边界条件示意图

图3 扁平箱梁局部网格示意图

1.3 参数定义及结果验证

扁平箱梁的阻力系数CD、升力系数CL和扭矩系数CM的定义分别为

CD=2FD/ρU2B

(4)

CL=2FL/ρU2B

(5)

CM=2MT/ρU2B2

(6)

式中，FD、FL、MT分别为顺风向阻力、横风向升力和扭矩；ρ为空气密度；U为风速；B为扁平箱梁宽度。三分力示意图如图4所示。

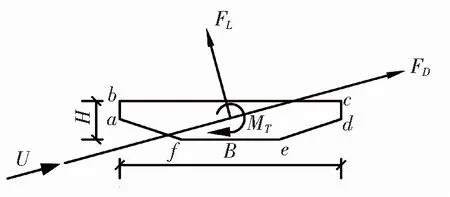
图4 三分力示意图

为了验证数值计算结果的准确性，将数值计算结果与文献[18]的风洞试验结果(宽高比B/H=5.78)进行了对比，如图5所示。从图5可以看到，对于阻力系数而言，数值计算结果和风洞试验结果略微有些差别，数值相差不大，但二者在变化规律上一致，均随风攻角的增大呈现出先缓慢减小后逐渐增大的变化规律。对于扁平箱梁的升力系数和扭矩系数，数值计算结果与风洞试验结果吻合较好。以上结果说明，数值计算结果具有一定的可靠性。

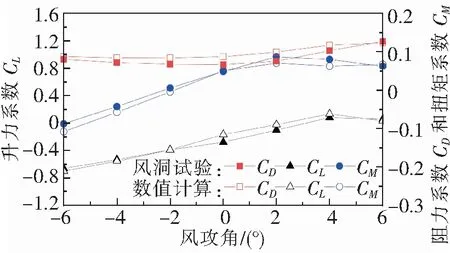
图5 宽高比为5.78时三分力系数的对比

2 宽高比对扁平箱梁气动力特性的影响规律

2.1 三分力系数

图6为不同宽高比下扁平箱梁的三分力系数随风攻角的变化曲线，从图6可以看到扁平箱梁在不同宽高比下的阻力系数随风攻角的变化规律基本一致，随着风攻角由-6°增加到6°，扁平箱梁的阻力系数先缓慢减小后逐渐增大，在风攻角为6°时达到其最大值，最大值为宽高比为5.0的时候，其最大值约为0.14。同时可以看到，随宽高比的增大，扁平箱梁在不同风攻角下的阻力系数均呈现出逐渐减小的规律。当风攻角为6°时，宽高比为5.0、5.78、8.0和10.0的扁平箱梁其阻力系数分别约为0.14、0.12、0.1和0.09。

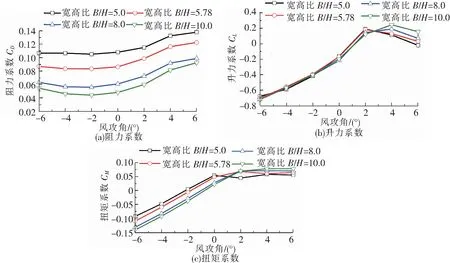
图6 不同宽高比扁平箱梁三分力系数随风攻角的变化曲线

扁平箱梁在不同宽高比下的升力系数均随风攻角的增加表现出了先增大后减小的变化规律。当B/H=5.0和5.78时，升力系数极大值发生在风攻角为2°时;当B/H=8.0和10.0时，升力系数极大值发生在风攻角为4°时。当风攻角为-6°～2°时，扁平箱梁在不同宽高比下的升力系数基本一致，随着风攻角的增加，由-0.7左右逐渐增加至0.2附近。当风攻角为4°～6°时，扁平箱梁的升力系数随宽高比的增大表现出了逐渐增大的规律。当B/H=5.0和5.78时，扭矩系数在风攻角达到0°时趋于平稳，当B/H=8.0和10.0时，扭矩系数在风攻角达到2°时趋于平稳。对比变扁平箱梁在不同宽高比下的扭矩系数可以看到，当风攻角为-6°～0°时，随着宽高比的增加扭矩系数呈现出逐步减小的变化规律，当风攻角为4°～6°时，随着宽高比的增加扭矩系数略有增大。当风攻角为-6°时，扭矩系数绝对值最大，宽高比为5.0、5.78、8.0和10.0的扁平箱梁其扭矩系数最大绝对值分别约为0.09、0.11、0.13和0.14。综合以上结果不难发现，宽高比的增加会使扁平箱梁受到的阻力减小，但会使其受到更大的升力和扭矩。

2.2 风压系数

扁平箱梁气动力特性的发生机理可通过风压分布进行分析[19-20]。为此，给出了不同宽高比下扁平箱梁表面的风压分布，如图7所示，需要说明的是，受篇幅限制，仅展示风攻角为±6°和0°。图7的风压系数定义为式(7)，其中P-P0为模型表面压力与参考压力的压力差。为便于描述，将扁平箱梁的角点依次记作a、b、c、d、e、f，如图4所示。记ab面、bc面及cd面分别为迎风侧直腹板、上顶板及背风侧直腹板，de面、ef面及fa面分别为背风侧斜腹板、下底板及迎风侧斜腹板。

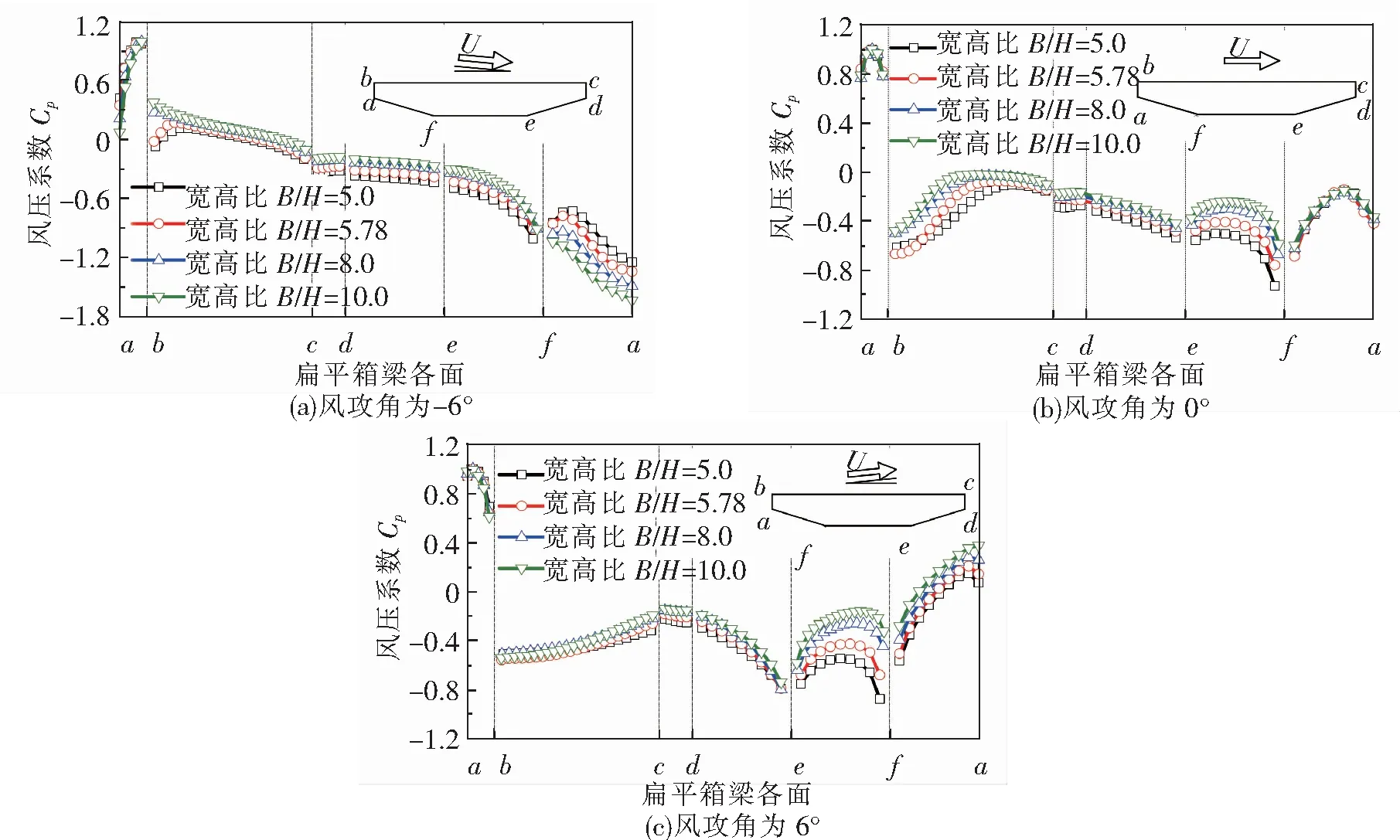
图7 不同宽高比扁平箱梁表面的平均风压系数

Cp=(P-P0)/0.5ρU2

(7)

图7为±6°和0°风攻角下不同宽高比下扁平箱梁表面平均风压系数随宽高比的变化曲线，从图7可以看到扁平箱梁在不同风攻角下的平均风压系数随宽高比的变化规律基本一致。在-6°风攻角下，不同宽高比扁平箱梁受正压的部分为ab面和部分bc面，其余部分均受负压的影响。不同宽高比扁平箱梁ab面的平均风压系数由角点a到角点b逐渐增大。扁平箱梁cd面和de面的平均风压系数变化幅度比ef面和fa面要小。在0°风攻角下，不同宽高比下扁平箱梁的平均风压系数仅有ab面为正值，其他面均为负值。在bc面上不同宽高比的负压由角点b到角点c表现出逐渐减小的规律。还可以明显看出在角点f附近受到的负压最大，其值约为-0.9。在6°风攻角下，不同宽高比扁平箱梁受正压的部分为ab面和靠近角点a的fa面，其余部分均受负压的影响。不同宽高比扁平箱梁ab面的平均风压系数由角点a到角点b逐渐减小。对于不同宽高比扁平箱梁的阻力系数，起主要影响作用的是扁平箱梁ab面、cd面、de面及fa面的风压。ab面的正压随着风攻角的增大变化不大，cd面、de面及fa面的负压随着风攻角的增大逐渐减小，所以cd面、de面和fa面的风压大小决定了箱梁阻力系数随着宽高比的增大而逐步减小。对于不同宽高比扁平箱梁的升力系数，起主要影响作用的是扁平箱梁bc面和ef面的风压，随着风攻角的增大bc面的负压越来越大，ef面的正压越来越大，同时也受到扁平箱梁de面和fa面的影响。从图7中可以看出扁平箱梁bc面和ef面的压力差随着宽高比的增大变化不明显，这较好解释了图6(b)升力系数规律的一致性。

3 气动力特性的流场机理分析

下面从流场角度来解释不同宽高比扁平箱梁风压系数的变化规律。图8为不同宽高比-6°风攻角下的时均流线图，从图8可以看到，不同宽高比扁平箱梁所形成旋涡的位置基本相同，均出现在扁平箱梁的cd面、fa面和de面附近，但旋涡大小不一。当宽高比为5.0时，扁平箱梁cd面、fa面和de面均出现了旋涡，对扁平箱梁产生负压作用；随宽高比的增大，扁平箱梁cd面形成的旋涡越来越小，致使扁平箱梁所受到的负风压逐渐减小，这验证了图7(a)中cd面和de面的平均风压系数绝对值随宽高比的增大而减小的变化规律。

图8 -6°不同宽高比箱梁时均流线图

图9为不同宽高比0°风攻角下的时均流线图，从图9可以看到,靠近角点b附近的旋涡中心随宽高比的增大，旋涡中心在逐渐向角点b移动。不难发现的是当旋涡随宽高比增大逐渐变小的时候，cd面附近仍有3个旋涡。当宽高比为5.0时，旋涡对扁平箱梁产生负压作用。随宽高比的增大，扁平箱梁cd面形成的旋涡越来越小，致使cd面和de面的平均风压系数绝对值随宽高比的增大而减小。

图9 0°不同宽高比箱梁时均流线图

图10为不同宽高比6°风攻角下的时均流线图，从图10可以看到，不同的宽高比所形成旋涡的位置基本相同。当宽高比为5.0和5.78时，扁平箱梁bc面、cd面均出现了旋涡。随宽高比的增大，扁平箱梁bc面形成的旋涡无明显变化，所以扁平箱梁bc面的风压变化表现不明显。但扁平箱梁cd面形成的旋涡随宽高比的增大越来越小，当宽高比为8.0时，扁平箱梁cd面不再形成旋涡，这致使cd面的负压随宽高比的增大而减小，所以扁平箱梁cd面的平均风压系数绝对值随宽高比的增大而减小。

图10 6°不同宽高比箱梁时均流线图

4 结论

基于数值模拟研究了-6°～6°风攻角范围内不同宽高比扁平箱梁的气动力特性，得到了以下结论：

(1)扁平箱梁的阻力系数随风攻角由-6°增大到6°呈现出先缓慢减小后逐渐增大的变化规律；升力系数呈现出先增大后减小的变化规律；扭矩系数呈现出先增大后趋于平稳的变化规律。宽高比的增加会使扁平箱梁受到的阻力减小，但会使其受到更大的升力和扭矩。

(2)不同的宽高比扁平箱梁所受的风压不同，扁平箱梁迎风侧直腹板所受风压基本不随宽高比发生变化，迎风侧斜腹板所受风压随宽高比的变化规律与风攻角有关，其他面所受风压随宽高比的增大呈现出逐渐增大的规律。不同的风攻角下扁平箱梁所受的风压也不同，随着风攻角的增大，上顶板所受负压越来越强，迎风侧斜腹板所受负压越来越弱。

(3)旋涡主要存在于扁平箱梁上顶板和尾流处，负攻角下在箱梁的迎风侧斜腹板处也有旋涡出现。不同宽高比下扁平箱梁所形成旋涡的位置基本相同，但大小和强度不同。箱梁上顶板所形成的旋涡对箱梁升力系数的大小起决定性作用。