变频凝泵结构共振分析与治理

许 辉, 温兴远, 夏亚磊, 吴亚军, 纪冬梅

(1. 上海电力大学 能源与机械工程学院，上海 201306;2. 中国大唐集团科学技术研究院有限公司中南电力试验研究院，郑州 450000;3. 中国联合工程有限公司，杭州 310052)

火电机组凝结水泵(简称凝泵) 采用立式袋筒型多级离心水泵(简称立式泵)，立式泵的电动机一般置于凝泵顶部，通过螺栓与泵体连接；同时，为了方便操作，泵体上开有多个小窗。泵体支撑刚度低，再加上凝泵顶部质量大，底部质量小的结构特征，导致其对外界激振力变化十分敏感。当凝泵变频运行时，常在某个频率段出现共振，导致振动过大，不得不调整转速，避开共振区间[1-2]。

目前，国内外对变频机组振动故障的研究大多从弯曲振动和共振角度出发。庞乐等[3]分析了凝泵结构共振的机理和故障特征，总结了激发共振的必备条件，并提出相应的治理措施。李新阳等[4]分别测试了凝泵电动机单转和连泵转2种状态下的振动响应，指出共振是由电动机转子和泵转子共同引起的。李年仔等[5]进行了凝泵弯曲振动试验，指出转子弯曲振动加速了凝泵导轴承与级间轴承的磨损，从而引发了转子-轴承-支撑系统的共振。

这些学者对变频凝泵振动故障机理进行了分析并从机械层面解释了共振原因，但均未考虑电气层面对共振的影响。笔者从机械与电气耦合(简称机电耦合)的角度解释了变频凝泵产生共振原因，并通过现场精细化动平衡方法成功解决了某2B凝泵在特定转速下振动大的问题。

1 凝泵结构共振分析

结构共振现象在旋转机械上十分常见，当转子的激振力能够克服定子阻尼，并且激振力的频率与凝泵一个或多个部件的固有频率接近时便会产生共振现象[6]。笔者对凝泵结构共振现象进行分析，找出共振的诱因。

1.1 凝泵轴系的扭转振动

该2B凝泵轴系结构简图见图1，该轴系主要包括导轴承、叶轮、联轴套管等部件。

图1 凝泵轴系结构简图

整个转子长约9 m，分上下半轴。下半轴靠近转子末端分布4级叶轮，集中质量较大。根据该2B凝泵轴系图纸，在ANSYS软件中建立了简化后的轴系实体模型，用MASS21单元模拟叶轮、平衡鼓。划分网格后的模型见图2。计算时，不考虑凝泵系统的阻尼，将轴系考虑成质量均匀的连续体，采用分块法求解得到凝泵轴系前四阶扭振频率(见表1)。

图2 凝泵轴系实体模型网格划分

表1 凝泵轴系前四阶扭振频率

由表1可知：凝泵轴系扭振的二阶固有频率为18.56 Hz，该频率所对应的转速落在凝泵常出现共振的转速区间(800～1 200 r/min)内。

由于MASS21单元仅能模拟叶轮、平衡鼓的质量效应与转动惯量效应，而忽略了刚性效应，导致最终的计算结果相对于实际结果偏小。但是，叶轮与平衡鼓结构特殊，其自身刚性效应弱，对轴系整体的刚性效应影响较小，所以表1的计算结果与实际结果相差不大。

1.2 变频电气系统理论分析

诱发共振需要一个激励源，大量研究表明，变频过程中逆变器产生的谐波是诱发旋转机械共振的源头。三相逆变器与异步电动机电路图见图3。

图3 三相逆变器与异步电动机

以图3电路为例，逆变器的输出电压Uad可以用傅里叶级数表示为：

Uad=∑Uabm(n)sinn(ωat)，n=1,3,5,…

(1)

式中：Uabm(n)为Uab第n阶谐波的电压幅值， V；t为时间，s；ωa为调制波频率，Hz。

由式(1)可得各阶谐波电压幅值的表达式[7]为：

cosn·(60-15M)-cosn·(60+15M)+

cosn·(90-15M)-cos 90n]

(2)

式中：U为直流母线侧的电压，V；M为调制比。

由式(2)可求出基波电压、3阶谐波电压、7阶谐波电压等的幅值，而这些谐波分量的频率分布可以表示为：

w=|p·wpwm±q·we|

(3)

式中：w为谐波分量频率，Hz；wpwm为载波频率，Hz；we为基波频率， Hz；p、q为0和正整数。

各组p和q的取值满足以下关系式：

(4)

或

(5)

或

(6)

该2B凝泵工频转速为1 500 r/min，根据负荷需求情况，其常用转速为825 ～1 180 r/min。该2B凝泵矢量变频控制器的载波频率选为300 Hz，其谐波频率分布见图4。

图4 谐波频率分布图

由图4可知：在变频转速区间内，凝泵轴系前三阶扭转固有频率与逆变器输出的低阶整数次谐波存在多个共振点，这表明当凝泵在变频区间运行时，受谐波影响，驱动电动机会产生与谐波频率对应的脉动扭矩，当该脉动扭矩的频率和凝泵轴系扭转固有频率接近时，就会产生结构共振。

2 凝泵结构共振情况

该厂300 MW机组配备2台100%容量的凝泵，电动机型号为YKSL450-4，水泵型号为NLTD450-8A。机组小修后对2B凝泵进行振动测试，现场架设2个振动速度传感器，分别位于电动机自由端水平、垂直方向，键相传感器位于垂直方向，见图5。

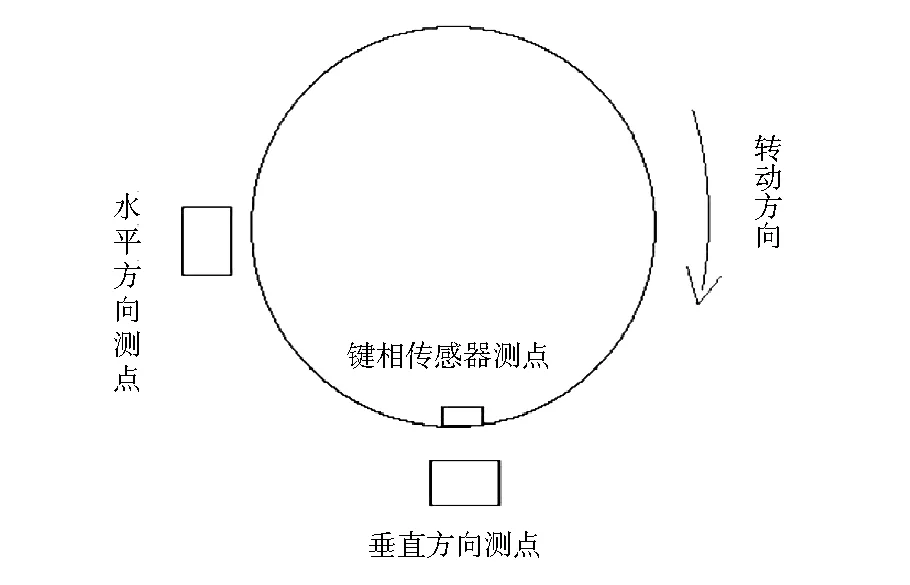
图5 传感器测点示意图

现场启动凝泵，缓慢将其升速至工频转速，测量升速过程中的振动情况，振动伯德(Bode)图和振动峰值分别见图6和表2。

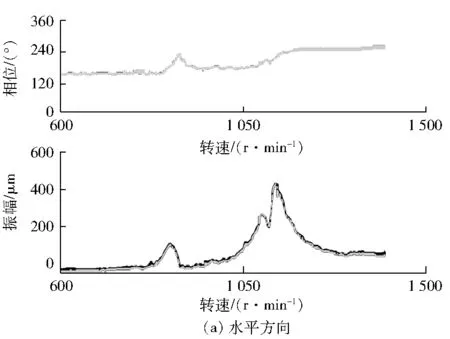
图6 凝泵启动过程Bode图

表2 各转速下振幅峰值

当电动机转速到达1 130 r/min时，水平方向的振动幅值达到445 μm，电动机自由端振动剧烈，继续升速到电动机工频转速(1 480 r/min)后，垂直方向的振动幅值仍有201 μm，严重超过运行标准。

3 原因分析

现场对凝泵进行停机检查，发现轴承紧力与间隙、联轴器开口度等参数均在设计值范围内，基本可排除轴承、联轴器的不对中、松动等问题。分析振动Bode图可知，水平方向振动在1 130 r/min时存在振动峰值，达到445 μm，转速由950 r/min升至1 150 r/min时，振动峰值相位变化约161°；在1 406 r/min时垂直方向有一个振动峰值，达到373 μm，转速从1 000 r/min升至1 200 r/min时，振动峰值相位前后变化约171°。升速脱离变频区间至工频后，水平方向幅值下降了351 μm。振动峰值点的频谱图见图7。由图7可知：激振力频率以基频为主，波形为简谐波。综上，判断振动大的主要原因是电动机产生的脉动扭矩频率与轴系扭转固有频率相近，导致结构共振。

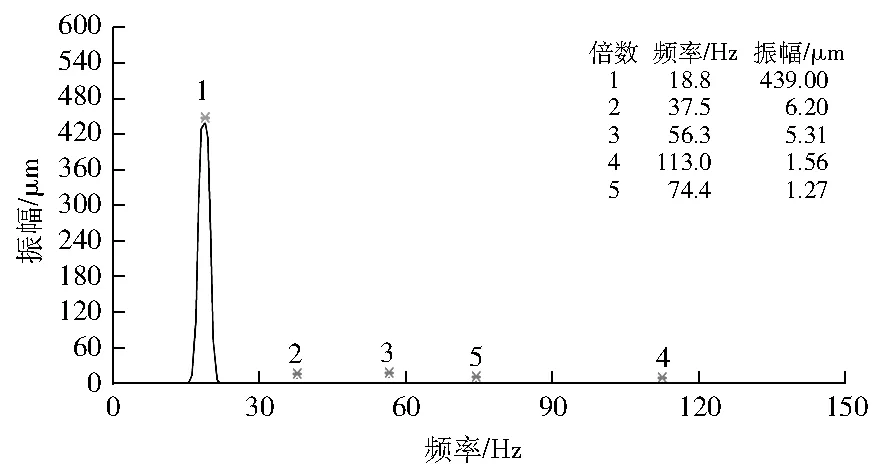
图7 凝泵电动机振动频谱图

4 处理措施

现场采用精细化动平衡的方法减轻共振。由于该2B凝泵电动机顶部无加重条件，只能在对轮联轴器处进行加重。现场准备了质量为300 g、500 g的加重垫片若干。以电动机水平方向幅值445 μm、相位69°为振动原始数据进行动平衡试加重计算，得到试加重的结果为800 g∠270°。加重后启机测得的数据见表3。

表3 试加重后各转速下振幅峰值

对比表2和表3发现：首次试加重后每个方向的振幅都有所下降，变频区间的振幅下降幅度为55%～69%。工频转速下的振幅同比下降56%～72%。但振幅仍未能达到预期，需要进行二次配重。

在试加重后的振幅和相位的基础上，根据线性振动理论求得影响系数，计算二次配重的校正位置和质量。计算公式如下：

αmu+A=0

(7)

式中：α为影响系数；mu为校正质量；A为原始振幅；mp为试加质量。

由式(5)计算得到二次加重方案为500 g∠300°。现场完成配重再次启机，测得各转速下的振幅峰值见表4。

表4 二次加重后各转速下振幅峰值

经过2次动平衡试验后，凝泵全频范围内的振动幅值均降至60 μm以下，动平衡方法取得了显著的减振效果。

配重前后凝泵振幅随转速变化见图8。

图8 配重前后振幅随转速变化曲线

由图8可知：经过动平衡处理后，凝泵常用变频区间的振动峰值较处理前下降幅度约为90%，工频转速下的振幅下降约为80%，达到预期。配重后的振幅曲线变化更加平缓，在变频调速时可以减少凝泵轴系的疲劳损伤累积。

5 结语

通过对某厂2B凝泵结构共振现象进行分析，发现变频器产生低阶整数次谐波分量是该凝泵产生结构共振的根源。该类谐波分量导致驱动电动机产生脉动扭矩，当脉动扭矩的频率与轴系、支撑结构的某阶固有频率接近时候就会引发结构共振。该诊断思路可为同类型故障诊断提供参考。

精细化动平衡技术目前仍是最有效、最经济的治理共振的手段，它能够有效降低凝泵变频共振区间内的振幅，减少调速时轴系的疲劳损伤。

从轴系扭振的角度寻找减振方案，可以改进变频器技术以减少谐波分量，从源头上抑制振动的产生。