深切河谷岸坡层状岩体倾倒变形演化过程及机理分析

司佳鹏， 张常亮，2， 赵 猛， 唐 斌， 李同录，2

（1.长安大学地质工程与测绘学院，西安 710054；2.黄土高原水循环与地质环境教育部野外观测研究站，甘肃庆阳 745399）

1973年，Freitas 和Watters［1］开始将岩体的倾倒变形破坏作为一种典型的破坏模式进行研究，随后岩体倾倒变形这一特殊地质现象越发引起了研究人员的关注. 随着我国水利工程建设的开展，更多的岩体倾倒变形现象被发现，如岷江、雅砻江、金沙江、澜沧江等上游地区的深切河谷边坡均发育了大量的岩体倾倒变形现象［2-4］. 由于该种岩体倾倒变形的形成过程及机理与一般岩体边坡的变形破坏存在较大差异，传统的岩体边坡稳定性分析方法很难被直接应用于该类边坡，给工程建设造成了极大的困扰.

很多学者利用物理模型试验对岩体倾倒变形的形成机理开展了研究，如左保成等［5］、卢增木等［6］经过一系列模型试验得出结构面强度、岩体层厚是对岩质边坡倾倒有比较大影响的因素；Amini等［7］通过倾斜试验台实验，成功模拟了岩质边坡的块体—弯曲倾倒破坏；Adhikary［8］经过离心试验发现，岩体结构面的摩擦角较大和较小时，倾倒变形破坏的表现形式为瞬时性和渐进性. 物理模型方法的优点是可以直观地记录边坡变形及其发展过程以及模拟边坡中岩体应力的大小及分布，缺点是模拟周期较长、费用较高等，所以进行的实验相对较少.

数值分析因其简便、经济及高效等优点，近年来被学者广泛应用于岩体倾倒变形机理的分析中. 如韩贝传和王思敬［9］、常祖峰等［10］、徐佩华等［11］、代仲海等［12］利用有限元法和有限差分法等连续介质分析方法对岩体倾倒变形进行了模拟，均取得良好的效果. 在现实中存在的边坡倾倒问题中，反倾的结构面将岩体分割成了离散但是又存在着相互联系作用的块体，这些块体单元在倾倒破坏时，会产生旋转和平移等破坏变形模式，这时，使用非连续介质力学方法可以更好地模拟这种变形破坏的模式. Sjöberg［13］、Lanar等［14］、程东幸等［15］、胡亚东等［16］、Scholtes和Donze［17］分别利用UDEC、3DEC等离散元对岩体倾倒变形进行了模拟，探讨了倾倒变形的影响因素和破坏过程. 由于非连续变形方法（DDA）可以考虑单元间复杂约束和接触关系，能处理任意凸边形或凹边形单元，允许单元脱离和错动，可有效模拟块体的大变形以及单元的转动特性，这些特性对边坡的倾倒变形研究有非常大的帮助，因此有学者尝试利用该方法对岩体倾倒变形进行分析，如孙亚东等［18］、龚文俊等［19］.

为此，本文使用DDA对黑河库区和镇安县深切河谷岸坡中厚层和薄层岩体倾倒变形问题进行分析，揭示了岸坡倾倒变形的演化过程和机理.

1 深切河谷岸坡层状岩体倾倒变形

1.1 黑河库区岸坡中厚层岩体倾倒变形

在黑河水库区域，黑河流经渭河盆地，在河流长期的侵蚀作用下，两岸形成了V型河谷，区域内存在多处大型古滑坡以及常见的范围较小的倾倒变形和崩塌等，如图1所示.

图1 黑河库区变形边坡及崩塌灾害Fig.1 Deformation slopes and collapse disasters in Heihe Reservoir

根据现场观察，河谷两岸岩体的结构是被片理和节理共同切割下形成的组合板状结构体. 岩体具板裂结构，溃曲破坏和弯曲变形是其发生的主要因素. 该边坡上主要有三组结构面，片理面S1倾向40°～75°，倾角28°～68°；一组节理面J1倾向287°～335°，倾角54°～75°；另一组节理面J2倾向196°～214°，倾角45°～88°.

该区域变质片岩构造节理发育，岩体结构被节理和片理共同切割，导致中厚层片岩边坡的破坏形式为块体崩塌. 岩块较为坚硬，而片理面抗剪强度非常低. 在黑河水流长期侵蚀作用下，在两岸坡脚处形成了坡度较大的临空面，从而导致反倾的岩体边坡向坡外发生弯折.

从图1（b）可以看出，路面以上约3 m处的边坡体有显著的倾倒弯折带，宽度约2 m. 弯折带产生的原因主要是中厚层状变质片岩的强度较高，边坡体的横向层理S1没有贯通，在后部坡体的推力作用下坡体根部的应力超过了岩块的抗拉强度，导致岩体发生折断，从而形成了弯折带. 同时，1号倾倒变形点比2号弯折变形更剧烈，这主要是由于1号点的河流侵蚀深度大于2号点造成的. 可见，河流长期侵蚀导致了边坡倾倒变形现象的发生，并且随侵蚀深度加深，边坡倾倒变形现象加剧.

由于弯折带处的岩体易聚积雨水，因此破碎的变质片岩会出现泥化现象，且这种现象会逐渐加重，就此形成软弱带，岩体的强度因此降低，弯折带以上岩体的变形增加，形成崩塌等灾害点，对水库的正常运营和坡下通过的省道形成了极大的安全隐患.

以上分析可见，黑河库区深切河谷岸坡的倾倒变形岩体，其形成主要是岩体力学性质、结构面分布特征和河流侵蚀共同作用的结果.

1.2 镇安县岸坡薄层岩体倾倒变形

该县城位于秦岭的断裂带之间，区域内发育有向斜、褶皱等地质构造，且多为岩性较软的薄层状千枚岩. 边坡的位置在县河的左侧，如图2所示.

图2 县河及薄层岩体倾倒变形Fig.2 Dumping deformations of county river and thin rock mass

边坡主要有三组结构面，一种为层理面S2，倾角在21°～42°之间，间距在0.5～1.5 cm之间；另外两种为构造剪切节理面J3、J4，J3倾向232°～286°，倾角73°～85°，J4倾向110°～172°，倾角60°～86°形成1～2 cm的裂隙.

该区域的地质活动强烈，年降雨大，千枚岩岩体破碎，遇水有严重的软化现象，长期冲刷作用下，会在坡脚处向外形成陡临空面. 而千枚岩裂隙中易储水，增加岩体自重，在雨水下渗的过程中，形成较大的水力坡度和力矩. 薄层千枚岩储水后呈现饱和状态，此种状态下承受水压力而发生断裂，而由于各处断裂位置不同，不能连接成断裂带，因此也不会发生大面积的滑动. 在长期降雨和河流侵蚀的作用下，边坡会逐渐地发生倾倒变形.

由以上分析可见，该边坡形成倾倒变形现象主要是地表降雨入渗、构造作用和河流侵蚀共同作用的结果. 构造作用是基础，降雨入渗是推动，河流侵蚀则会造成岩体主应力方向的变化，这是倾倒变形发生的根本原因.

综上所述，河流侵蚀是造成中厚层和薄层岩体边坡倾倒变形的关键因素，要想揭示该种变形发生发展的本质，就需要建立起长期河流侵蚀作用下岸坡岩体变形的模型，考虑到河流侵蚀作用是一个漫长的地质过程，物理模型试验等手段很难满足其要求，数值分析则为其提供了很好的分析方法.

2 岩石及结构面力学特性

2.1 岩石力学特征

黑河库区和镇安县岸坡的岩性分别以变质片岩和千枚岩为主，对其进行饱和重度测试、单轴压缩试验和直剪试验，整理后获得岩石物理力学参数值，如表1所示.

表1 岩石物理力学参数Tab.1 Physical and mechanical parameters of rock

2.2 结构面力学特征

对于中厚层和薄层岩体边坡每组结构面现场测量其轮廓曲线长度Ln（cm）；裂面起伏度Ry（cm），利用巴顿的图解法获得其对应的JRC 值，在每组结构面上，做回弹试验，获得其JCS 值，基于Barton的JRC-JCS模型，获得了各结构面下剪应力和法向应力的关系，进而获得各结构面的抗剪强度指标，如表2所示.

表2 岩体结构面抗剪强度估算结果Tab.2 Estimation results of shear strength of rock mass structural plane

3 非连续变形理论及改进

在目前的非连续介质力学方法中，二维DDA 方法［20］可以同时考虑块体之间的不连续变形、本身的大变形和模拟出单元的转动特性. 在二维DDA方法中，岩体的主要变形是沿结构面的变形，这与结构面对倾倒变形的控制是一致的. 该方法可以使不连续面所切割的块体系统重新连接成一个统一的整体进行模拟计算，从而可以对岩体的局部稳定性和整体的动态进行模拟分析，得到较准确的分析.

作为一种数值模拟方法，二维DDA 方法也有其局限性，此方法只能针对单一的工况做出模拟. 在河流长期的侵蚀下，边坡发生倾倒变形现象是一种长期的、连续的过程，需要建立不同的侵蚀阶段，每一阶段完成后，边坡的形状、节理、位移场和应力场等都会重新分布，而运用二维DDA 方法进行计算时，每一阶段都是从原始坡面开始计算，这显然是不对的.本文为了解决此问题，利用提取坡面数据、节理、单元的应力场和位移场数据的方法，在DDA 的DC 程序中，对坡面和节理数据进行互相替换，将前一个工况的模拟结果作为下一个工况的初始模拟条件来达到进行分步下切计算的目的. 该种方法的流程图如图3.

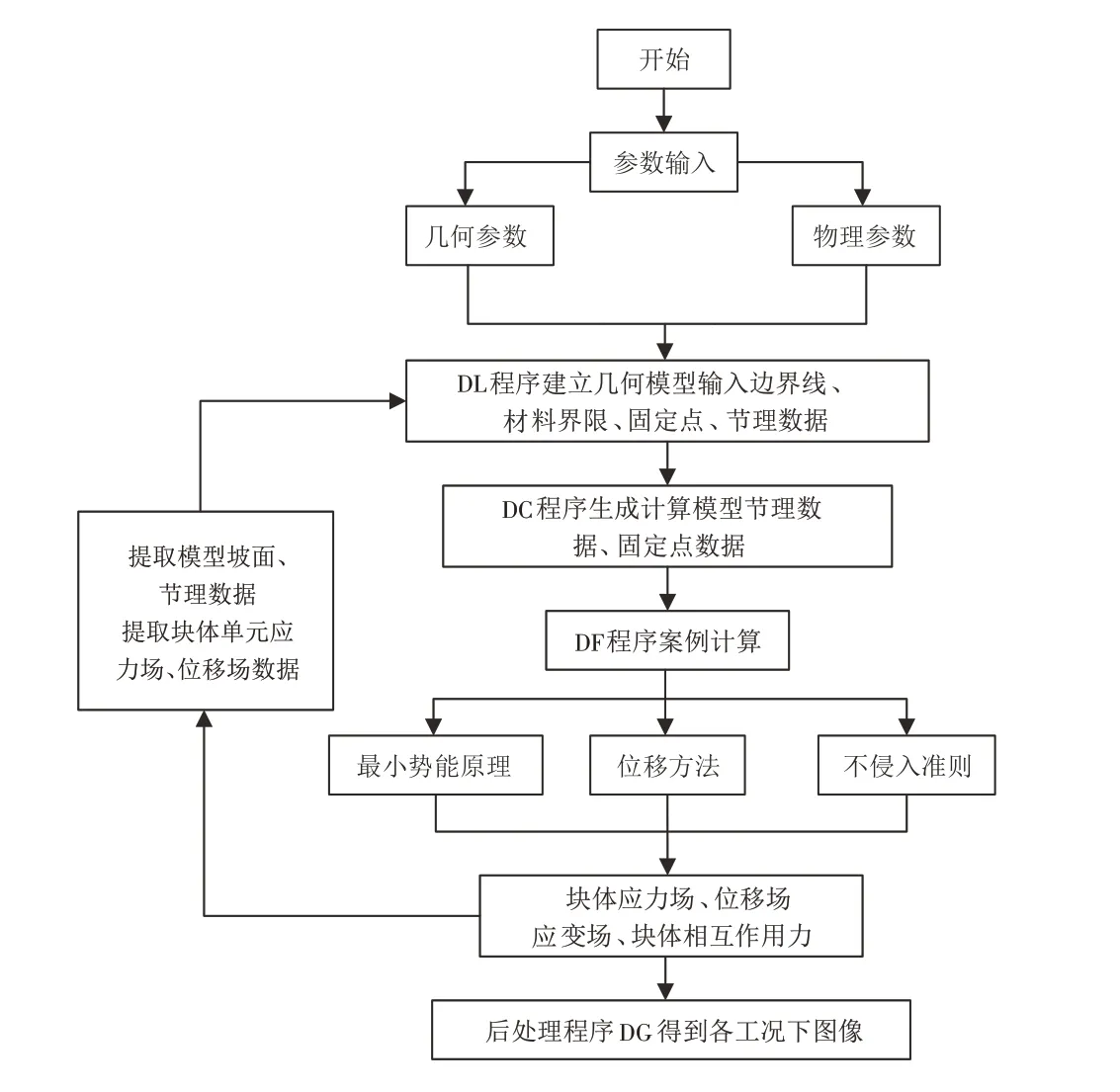
图3 DDA改进方法计算流程图Fig.3 Calculation flow chart of DDA improvement method

4 岩体倾倒变形演化过程模拟及机理研究

4.1 黑河库区边坡倾倒变形演化过程模拟

黑河库区两岸的边坡岩体呈中厚层状，在构建DDA 二维模型的时候，节理J2的间距取为6 m. 根据资料可以得知，河流对此区域的侵蚀速率为0.10～0.15 m/ka，由于区域的岩性比较硬，所以在使用DDA模型进行模拟计算时，侵蚀速率取0.1 m/ka. 以目前的地面为最终的工况，一个侵蚀阶段取100 ka，初始工况为向前倒推三个侵蚀阶段，即300 ka. 选取边坡的横向节理S1（73°∠28°）、竖向节理J2（202°∠82°）以及根据现场的实测剖面和推测地面线，在DDA中构建二维模型，见图8. 在模型的右侧坡面布置了5个监测点（图4），用来监测边坡模拟倾倒变形过程中应力场和位移场的变化. 各阶段侵蚀示意图见图5.

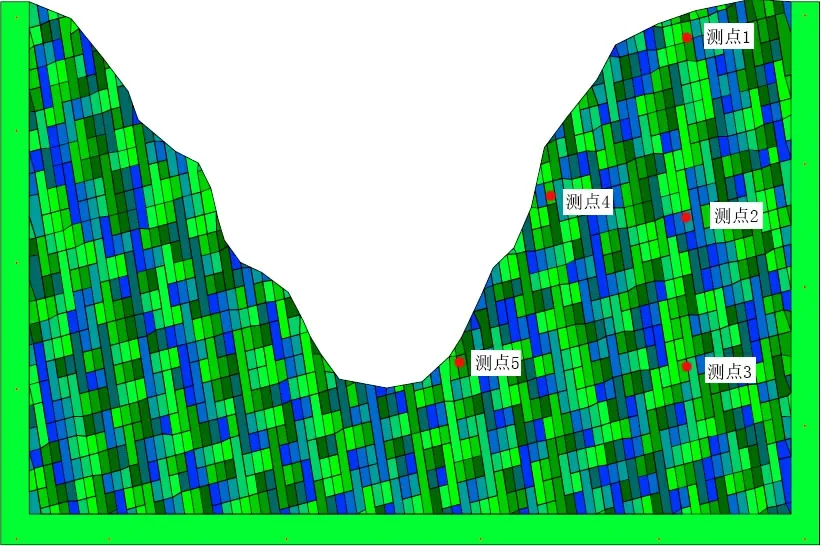
图4 二维DDA模型Fig.4 Two dimensional DDA model

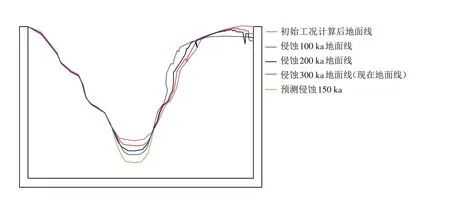
图5 各阶段侵蚀示意图Fig.5 Schematic diagram of erosion in each stage

利用二维DDA 的改进方法进行河流侵蚀作用下边坡倾倒变形过程的模拟. 图6 分别为初始工况（工况1）、侵蚀100 ka（工况2）、侵蚀200 ka（工况3）、侵蚀300 ka（现在的地面线）（工况4）的模型和模拟计算结果图.

图6 各工况下模型及计算结果Fig.6 Models and calculation results under various working conditions

从图6所展示的不同阶段工况可以看出，在初始工况的计算结果模型中，竖向组节理J2已经有轻微的拉裂，整个边坡此时已经开始发生松动；而在侵蚀时间为100 ka时，边坡上部发生微小的弯折，更多的节理的开始拉裂，并且有小范围的崩塌；在侵蚀时间为200 ka时，边坡的上部弯折显著，弯折带明显，并且坡角处有轻微的拉裂变形；在侵蚀时间为300 ka时，可以看出倾倒带从坡体的内部一直延长到坡脚，而上部的弯折倾倒继续增加，坡脚的岩体也随之开始松动. 将侵蚀时间为300 ka时的边坡局部倾倒变形和调查时现场的图片作对比（图7）可以发现，此时的模拟结果和实际考察的情况比较接近，这说明了此次模拟比较好地还原出了边坡的倾倒变形过程.

图7 现场观测和模拟结果对比Fig.7 Comparison of field observation results and simulation results

以侵蚀300 ka（现在地面线）计算结果作为下一阶段初始条件对边坡的未来变形作预测，选取不同的侵蚀时间进行计算，发现继续侵蚀时间为150 ka 时（工况5），边坡的倾倒现象非常显著，此时已经发生破坏，计算结果见图8.

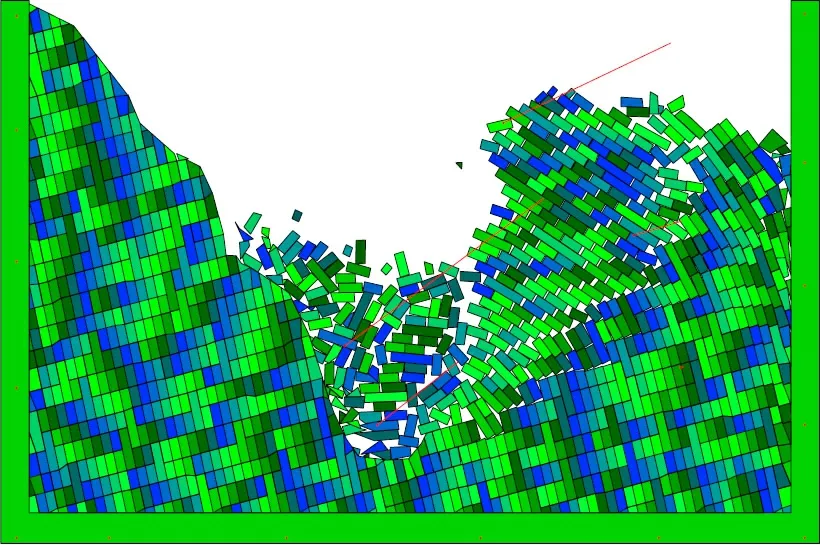
图8 现有地面线继续侵蚀150 ka计算结果Fig.8 Calculation results of 150 ka continuous erosion of existing ground line

4.2 黑河库区边坡岩体倾倒变形机理研究

五个监测点在边坡倾倒过程中的水平方向和竖直方向的位移随迭代步数的关系曲线以及选取边坡内部的监测点1、2、3处块体单元的转角随着迭代步数的变化曲线见图9.

图9 监测点位移和转角变化图Fig.9 Displacement and rotation angle change diagrams of monitoring points

边坡在发生倾倒变形的过程中会形成弯折带，通过对边坡位移和转角随迭代步数的变化曲线可以看出，在弯折带的上方（监测点1、4）位移和转角都会有明显的增大，弯折带附近的岩体（监测点2）在边坡破坏时位移和转角显著增大，而下方（监测点3、5）变化较小，监测点3在整个演化过程中几乎不变. 在弯折带出现和贯通时，都会出现位移突然变化的情况，所以竖向位移、水平位移、转角三者与迭代步数的关系曲线都呈现出“稳定—突变—稳定—突变”的特点. 通过以上分析，可以将河流侵蚀作用下中厚层岩体边坡的弯折倾倒全过程总结归纳为以下五个阶段：应力重组阶段、初始弯折阶段（工况2和工况3的前半段）、弯折突变阶段（工况3的后半段）、弯折稳定阶段（工况4）、破坏阶段（工况5）.

从力学方面研究此边坡倾倒变形破坏的机制，首先需要提取出边坡在倾倒变形破坏过程中的应力场数据，再通过摩尔-库伦破坏理论得到监测点1、4、5处主应力大小随迭代步数的变化曲线、大主应力与x轴正方向的夹角θ的变化曲线（图10）.

从图10可以看出，随着倾倒变形过程的发展，边坡监测点的大小主应力整体呈增大趋势. 坡脚监测点5的大小主应力都是最大的，说明在河流侵蚀下坡脚卸荷造成应力集中现象. 随着边坡发生倾倒变形，坡面处的监测点1、4大主应力与x轴的夹角逐渐增大，而坡脚监测点5大主应力与x轴的夹角呈现减小的趋势，从近乎和坡面平行方向向水平应力方向靠近，在工况5边坡发生破坏时，大主应力方向发生起伏变化.

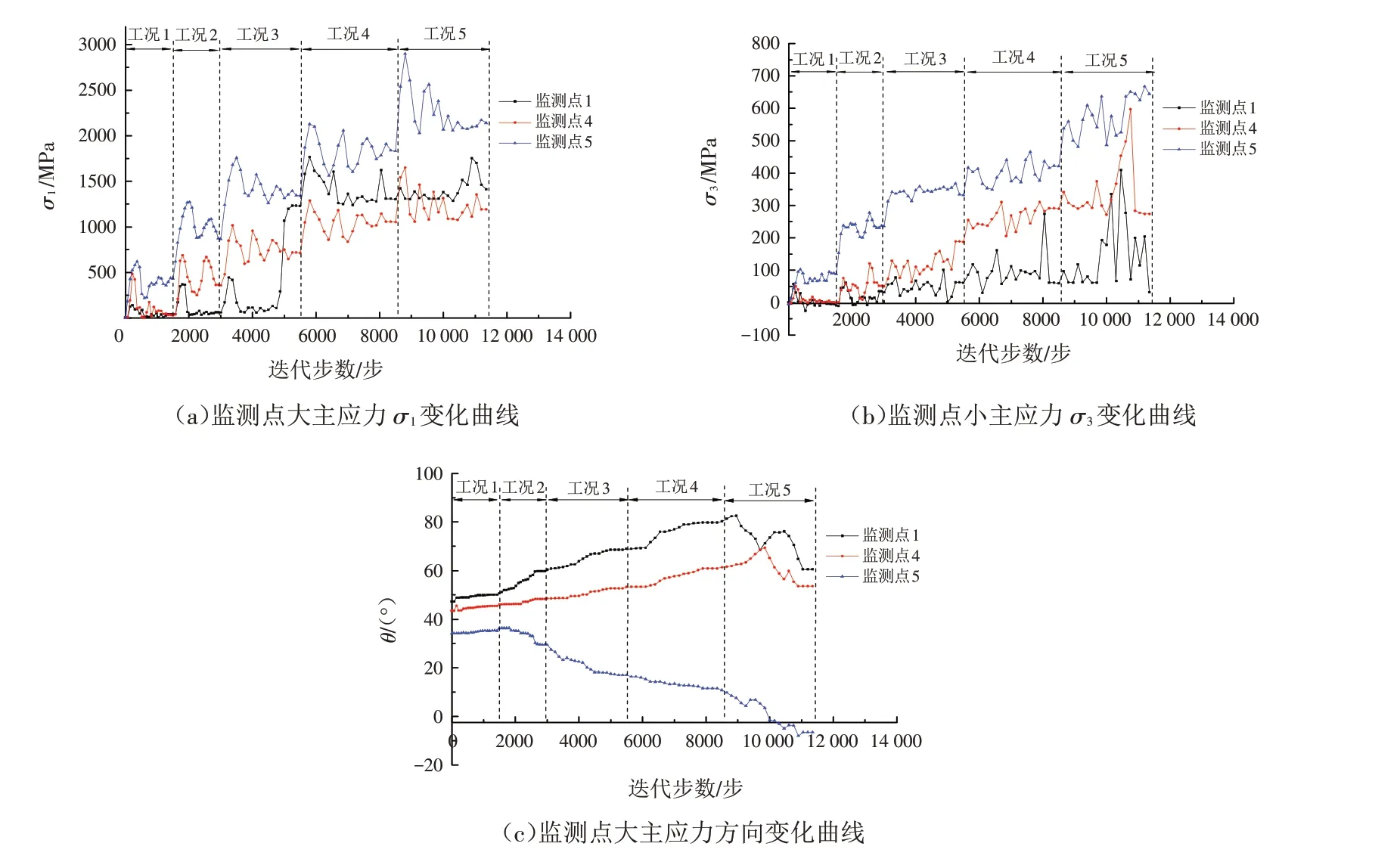
图10 监测点主应力大小和方向变化图Fig.10 Changes in the magnitudes and directions of the principal stresses at the monitoring points

4.3 镇安县边坡倾倒变形演化过程模拟

镇安县两岸的边坡岩体呈薄层，在构建DDA 二维模型的时候，河流对此区域的侵蚀速率取0.15 m/ka.以目前的地面为最终的工况，一个侵蚀阶段取50 ka，初始工况为向前倒推三个侵蚀阶段即150 ka. 选取边坡的层理面S2（350°∠30°），竖向节理J4（142°∠74°）以及根据现场的实测剖面和推测地面线，在DDA中构建二维模型，见图11. 在模型的右侧坡面布置了八个监测点（图11），用来监测边坡模拟倾倒过程中的应力场和位移场变化. 各阶段侵蚀示意图见图12.

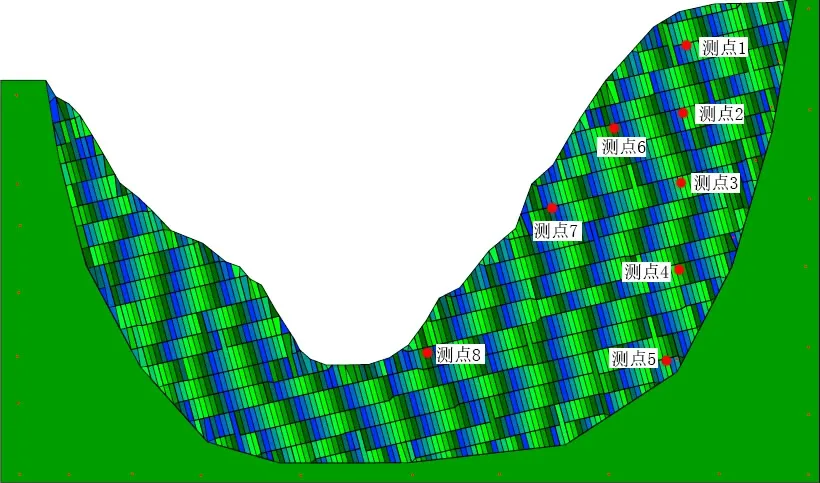
图11 二维DDA模型Fig.11 Two dimensional DDA model

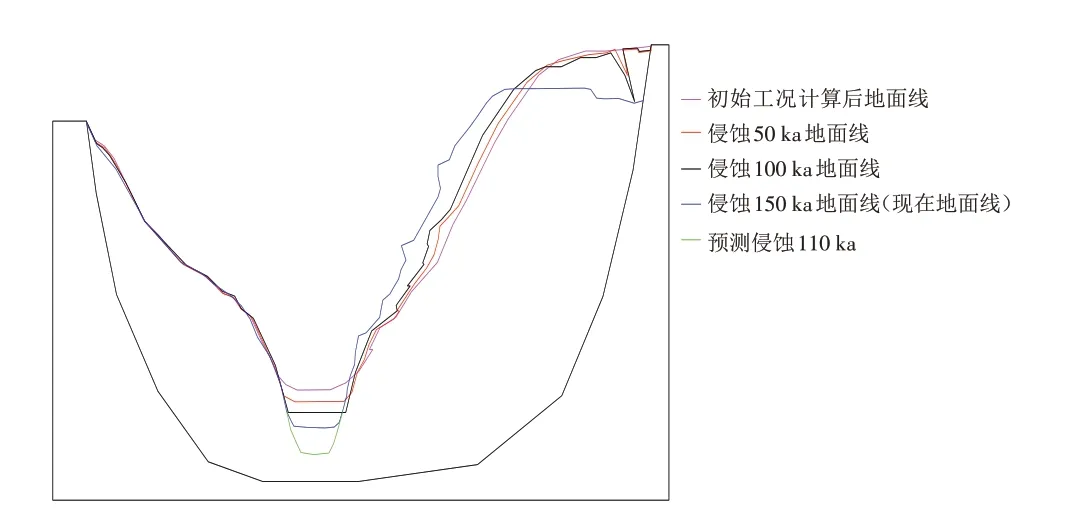
图12 各阶段侵蚀示意图Fig.12 Schematic diagram of erosion in each stage

图13分别为初始工况（工况1）、侵蚀50 ka（工况2）、侵蚀100 ka（工况3）、侵蚀150 ka（工况4）（现有的地面线）的模型和模拟结果.

图13 各工况下模型及计算结果Fig.13 Models and calculation results under various working conditions

从图13 可以看出，当侵蚀50 ka 时，边坡的后缘出现拉裂缝并沿着竖向节理J4 向边坡内部延伸. 侵蚀100 ka时，坡体的变形加大，出现更多的竖向裂隙，并且伴有小块体滑落. 侵蚀150 ka时，坡体的变形剧烈，发生明显的倾倒变形现象，大量的小块体滑落，岩体会顺着层理面S2的方向发生微滑移. 侵蚀150 ka时，坡体向外弯曲形成临空面，但是没有沿层理面S2发生倾倒破坏，为了探究这种原因，对此种工况下的边坡局部图进行研究，如图14. 可以看出，此时竖向节理J4发生明显的弯曲，而层理面S2则变化较小，但是块体在层理面S2的接触方式由边边接触变为边角接触，导致层理面S2呈现规则的“锯齿”状，面摩擦变为楔摩擦，出现爬坡效应，结构面的强度提高.

图14 侵蚀150 ka边坡局部特征图Fig.14 Local characteristic map of slope eroded 150 ka

以侵蚀150 ka（现在地面线）计算结果作为下一阶段初始条件对边坡的未来变形作预测，选取不同的侵蚀时间进行计算，发现继续侵蚀时间为110 ka时（工况5），边坡此时已经发生破坏，计算结果见图15.

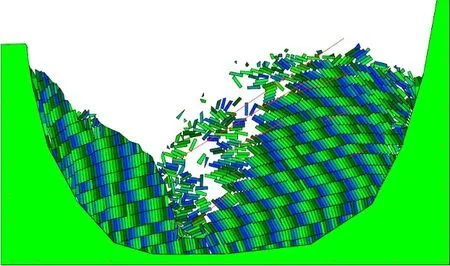
图15 现有地面线再侵蚀110 ka计算结果Fig.15 Calculation results of 110 ka re-erosion of existing ground line

4.4 镇安县边坡岩体倾倒变形机理研究

八个监测点在边坡倾倒过程中的水平方向和竖直方向的位移随迭代步数的关系曲线以及选取边坡内部的监测点1～5处块体单元的转角随着迭代步数的变化曲线见图16.

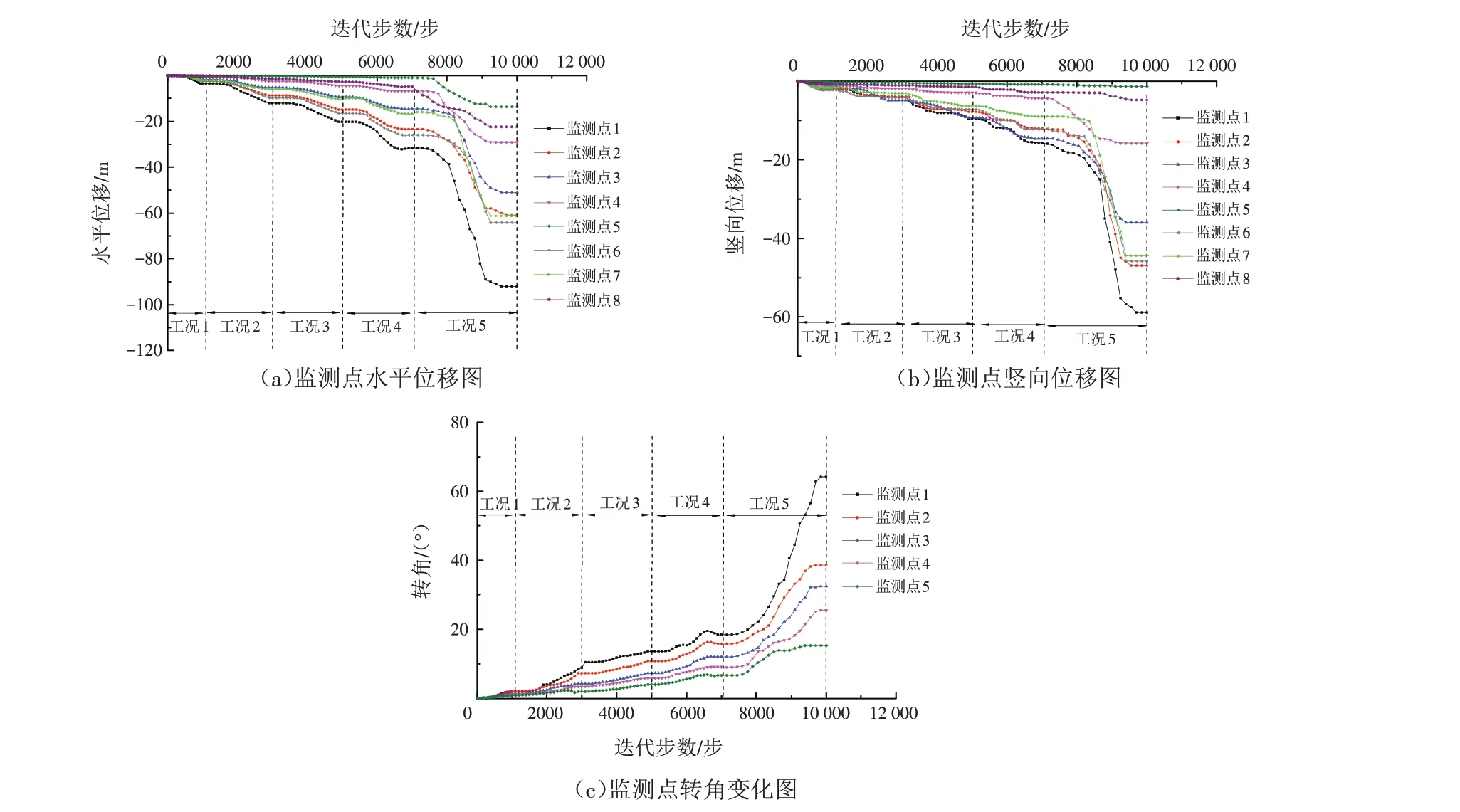
图16 监测点位移和转角变化图Fig.16 Displacement and rotation angle change diagrams of monitoring points

通过对边坡位移和转角随迭代步数的变化曲线可以看出，边坡浅层的监测点（监测点1、2、6、7）位移和转角较大，坡顶监测点1最大；而坡脚和边坡深部（监测点3、4、5、8）的位移和转角则较小. 通过以上分析，可以将河流侵蚀作用下薄层岩体边坡的弯折倾倒全过程总结归纳为以下五个阶段：应力重组阶段、坡顶拉裂变形阶段（工况2前半段）、初始倾倒变形阶段（工况2后半段和工况3）、倾倒-滑移变形阶段（工况4）、破坏阶段（工况5）.

从力学方面研究此边坡倾倒变形破坏的机制，提取出边坡在倾倒变形破坏过程中的应力场数据，再通过摩尔-库伦破坏理论得到监测点1、6、7、8处主应力大小随迭代步数的变化曲线、大主应力与x轴正方向的夹角θ的变化曲线（如图17）.

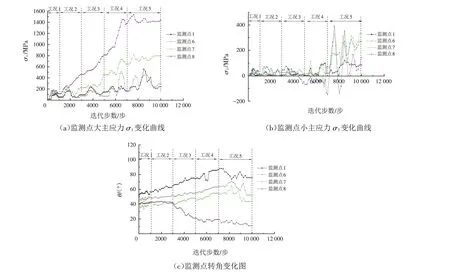
图17 监测点主应力大小和方向变化图Fig.17 Changes in the magnitudes and directions of the principal stresses at the monitoring points

从图17可以看出，随着倾倒变形过程的发展，边坡监测点的大小主应力整体呈增大趋势. 坡脚监测点8的大主应力是最大的，说明了在河流侵蚀下坡脚卸荷造成应力集中；而浅表层各测点的小主应力在坡体破坏前较小，破坏后出现剧烈的起伏，说明此时的边坡不稳定. 随着边坡发生倾倒变形，坡体浅层的监测点1、6、7大主应力与x轴的夹角逐渐增大，与坡面保持平行；而坡脚处监测点8大主应力与x轴的夹角逐渐减小，从近乎和坡面平行方向向水平应力方向靠近，在工况5边坡发生破坏时，大主应力方向发生起伏变化.

4.5 中厚层和薄层岩体倾倒变形现象对比分析

通过上述分析我们可以得出，在倾倒变形过程中，中厚层岩体会在边坡内形成弯折带，弯折带上部和下部的变形存在较大的不同，整个倾倒变形过程可以分为五个阶段，在弯折带出现和贯通时，都会出现位移突然变化的情况. 薄层岩体则不会在边坡内形成弯折带，坡体内各个部分的变形数据逐渐增长，整个倾倒变形过程也可以分为五个阶段.

在倾倒变形机理分析中，中厚层和薄层岩体边坡都表明，深切河谷岸坡层状岩体发生倾倒变形的根本原因是坡体所受大主应力方向的偏转，坡体浅表层大主应力的方向随着倾倒变形的发展而不断变化，保持和坡面平行的状态，而坡脚处的应力集中现象使得此处大主应力的方向向坡内变化并逐渐趋于水平，也导致此处结构面的强度变大，变形较小. 二者的不同点从剪应力的变化曲线上可以看出，如图18，薄层岩体边坡由于不存在弯折带，因此在坡脚处（监测点8）剪应力最大，在坡体内部各监测点处则较小，而中厚层岩体边坡则由于存在弯折带，导致弯折带（监测点2）附近的剪应力最大，而坡脚处的剪应力较小，弯折带隔断了坡体深部的弯折效应，所以中厚层岩体边坡倾倒变形现象主要存在浅表部.

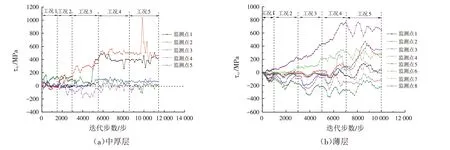
图18 监测点剪应力τxy变化曲线Fig.18 Variation curves of shear stress τxy at each monitoring point

4.6 中厚层岩体边坡支护方案

通过上述研究，选择中厚层岩体边坡进行支护设计模拟，选择侵蚀300 ka（现有地面线）的结果进行预应力锚索支护，一共添加六根锚索，从上往下编号为1～6，上面三根长度为60 m，穿过弯折带，下面三根长度为45 m，锚索添加的方向为与水平面夹角为30°. 锚索参数：弹性模量25 000 MPa；抗拉强度2000 MPa；预应力值1200 kN，示意图见图19.

图19 锚索支护示意图Fig.19 Schematic diagram of anchor cable supports

对支护后的边坡进行迭代求解，在1500步时计算收敛，提取监测点1～5的位移数据和锚杆的锚固力数据，监测点1～5的水平和竖向位移在支护后明显减小，边坡没有破坏，起到了很好的支护效果. 从图20可以看出锚索锚固力随着迭代而逐渐增大，最靠近坡顶的锚索1锚固力最大，穿过弯折带的锚索1～3的锚固力变化明显，下面三根锚索4～6 变化则较小，锚索6 锚固力最小.

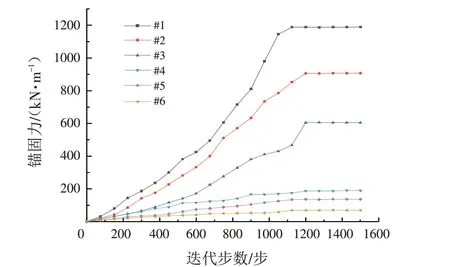
图20 锚索锚固力变化曲线Fig.20 Variation curves of anchor cable anchoring forces

5 结论

本文以陕西省西安市黑河库区左岸边坡和镇安县县河左岸边坡为例，利用DDA数值方法，探究了深切河谷岸坡层状岩体边坡在河流侵蚀下发生弯折倾倒变形的演化过程和机理，得出以下结论：

1）根据实地观测和分析，黑河库区中厚层岩体边坡发生倾倒变形主要是岩体力学性质、结构面分布特征和河流侵蚀共同作用的结果. 镇安县薄层岩体边坡发生倾倒变形主要是地表降雨入渗、构造作用和河流侵蚀共同作用的结果.

2）针对二维DDA只能计算单一工况的问题，利用提取坡面数据、节理、单元的应力场和位移场数据的方法，将前一个工况的模拟结果作为下一个工况的初始模拟条件进行分步下切计算，成功模拟了边坡在河流分步侵蚀下的倾倒变形.

3）利用建立起的河流侵蚀岸坡岩体边坡模型，对岩体倾倒变形演化过程进行了模拟分析，将河流侵蚀作用下中厚层岩体边坡倾倒变形过程划分为应力重组、初始弯折、弯折突变、弯折稳定以及破坏五个阶段，薄层岩体边坡倾倒变形过程中会出现爬坡效应，将其划分为应力重组、坡顶拉裂变形、初始倾倒变形、倾倒-滑移变形以及破坏五个阶段. 为河流侵蚀作用下岩体倾倒变形边坡的防护提供了机理参考和防护依据.

4）边坡发生倾倒变形的根本原因是坡脚的结构面强度变大，坡顶应力释放导致的主应力方向发生偏转. 倾倒变形的模式则是由剪应力分布情况决定的.

5）通过对深切河谷岸坡层状岩体倾倒变形演化过程和机理的研究，对中厚层岩体倾倒变形边坡进行锚索支护模拟，相较于预测工况，计算后边坡各处的位移明显减少，从坡顶到坡脚施加的锚索的锚固力逐渐减小.