k/n(G)可修系统的多水平修理策略优化

刘 聘， 董庆来， 周楚钰

（延安大学数学与计算机科学学院，陕西延安 716000）

k/n(G)系统是可靠性数学理论中十分重要的基本模型之一，系统由n个部件组成，至少有k个部件正常工作时，系统正常运行［1-3］.k/n(G)系统具有广泛的实际应用领域，研究人员对此类系统可靠性问题进行了大量的研究［4-6］. Hamdan等［7］考虑对一类加权n中取k系统引入新的最优预防性维护模型；Zhang等［8］针对具有失效依赖的n中取k退化系统研究了一种基于状态的维护策略；Krishnamoorthy 等［9］将N-策略应用于k/n(G)系统，该策略是指系统中的故障部件数达到预定N值时，系统指派修理工维修故障部件；付永红等［10］在此基础上建立一个无储备部件的并联非马氏机器维修模型，研究了一种新型的两水平(r,s)修理策略，通过预定阈值合理有效地指派两个等级的修理工进行修理工作；吴文青等［11］基于Krishnamoorthy［9］和付永红等［10］的成果，以达到合理配置人力资源为目的，研究了具有两水平修理策略和两类修理工的表决可修系统. 此外，张元元和吴文青［12］假设k/n(G)系统的修理设备可更换，讨论专职修理工多重休假问题；左凯等［13］对修理工多重休假且修理设备可更换的n中取k温储备系统可靠性进行分析；刘鸿彬等［14］对r/n(G)系统的剩余寿命预测问题进行研究.

在实际当中，例如对某地多个信号传输塔的维修，信号塔可能由于内部原因或外部冲击发生故障，而进行维修工作的修理工按照修理能力的不同被分为多个级别. 如何在考虑部件竞争失效的情况下合理配置人力资源的问题未能解决，因此，本文研究具有多水平修理策略的k/n(G)表决可修系统，系统中的部件可能由于内部故障或外部冲击发生故障. 利用马尔可夫分析方法，推导了系统可用度等可靠性指标表达式. 通过调整多水平修理策略，最小化系统期望成本. 最后，以三水平修理策略为例，验证了研究结果的实用性.

1 模型描述

具有多水平修理策略的k/n(G)系统模型假设如下.

1）系统由n个同型部件组成，每个部件有正常工作和故障两种状态，系统涉及的随机变量彼此独立.

2）部件的寿命分布服从负指数分布F(t)=1-e-λt，0 ＜λ＜∞，t≥0，且部件独立故障率为λ.

3）该系统在冲击环境下工作，冲击的到来遵循齐次泊松过程，速率为v. 如果冲击是致命的，它会引起部件故障且相应的概率是p0；认为非致命冲击对部件没有影响，概率为1-p0.

4）有l个级别的修理工且其修理时间服从参数分别为μ1，μ2，…，μl的负指数分布G(t)=1-e-μjt，0 ≤μ＜∞，t≥0，j=1，2，…，l. 所述的级别是按修理能力进行划分的，修理能力越高，级别越高. 当工作部件发生故障时，系统将根据多水平修理策略指派各级修理工修理故障部件，其中，多水平修理策略表示为(d1,d2,…,dl)，0 ≤d1≤…≤dl≤n-k+1. 当系统中的故障部件数达到d1值时，系统立刻指派一级修理工进行维修工作.若修理工作顺利，故障部件修理完毕，则一级修理工撤出系统；若修理工作不顺利，故障部件数持续增加到d2值时，系统立刻指派二级修理工，若修理工作顺利，故障部件数小于d2值时，二级修理工撤出系统，由一级修理工继续进行修理工作，直到故障部件修理完毕，若在此期间，故障部件数又一次达到d2值，则二级修理工再次进行修理工作. 以此类推，若故障部件数持续增加到dl值时，此时系统指派l级修理工，若故障部件数达到n-k+1，则系统发生故障，此时其余k-1 个部件不再发生故障. 其中，假设各级修理工对故障部件的修理为完全维修.

令L(t)表示时刻t系统中有i个部件处于故障状态（包括在修理中的部件），L(t)=i，i=0，1，…,n-k+1.令J(t)表示时刻t系统指派某级修理工修理故障部件，设

多水平(d1,d2,…,dl)修理策略的系统维修流程如图1所示，根据模型描述和状态转移图易知，随机过程{L(t),J(t)|t≥0} 的状态空间为

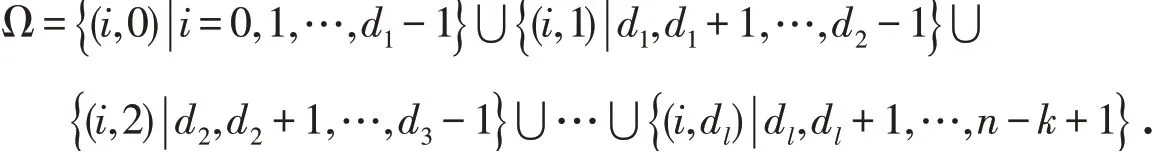
图1 多水平修理策略系统维修流程图Fig.1 The system repair flow chart with the multi-level maintenance strategy

为了方便讨论，记ξi=(n-i)(λ+vp0),i=0,…,n-k，系统的状态转移图如图2所示.

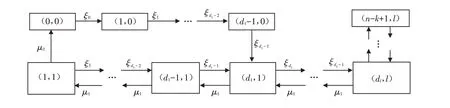
图2 系统状态转移图Fig.2 State transition diagram of the system

假设系统的稳态概率表示为：

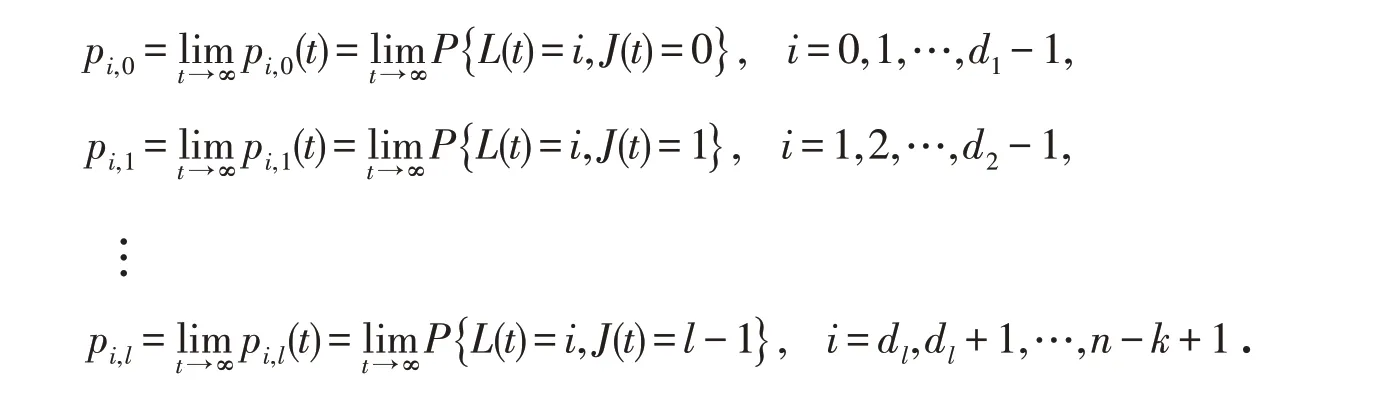
根据马尔可夫过程理论和系统状态转移图，系统稳态概率满足如下方程

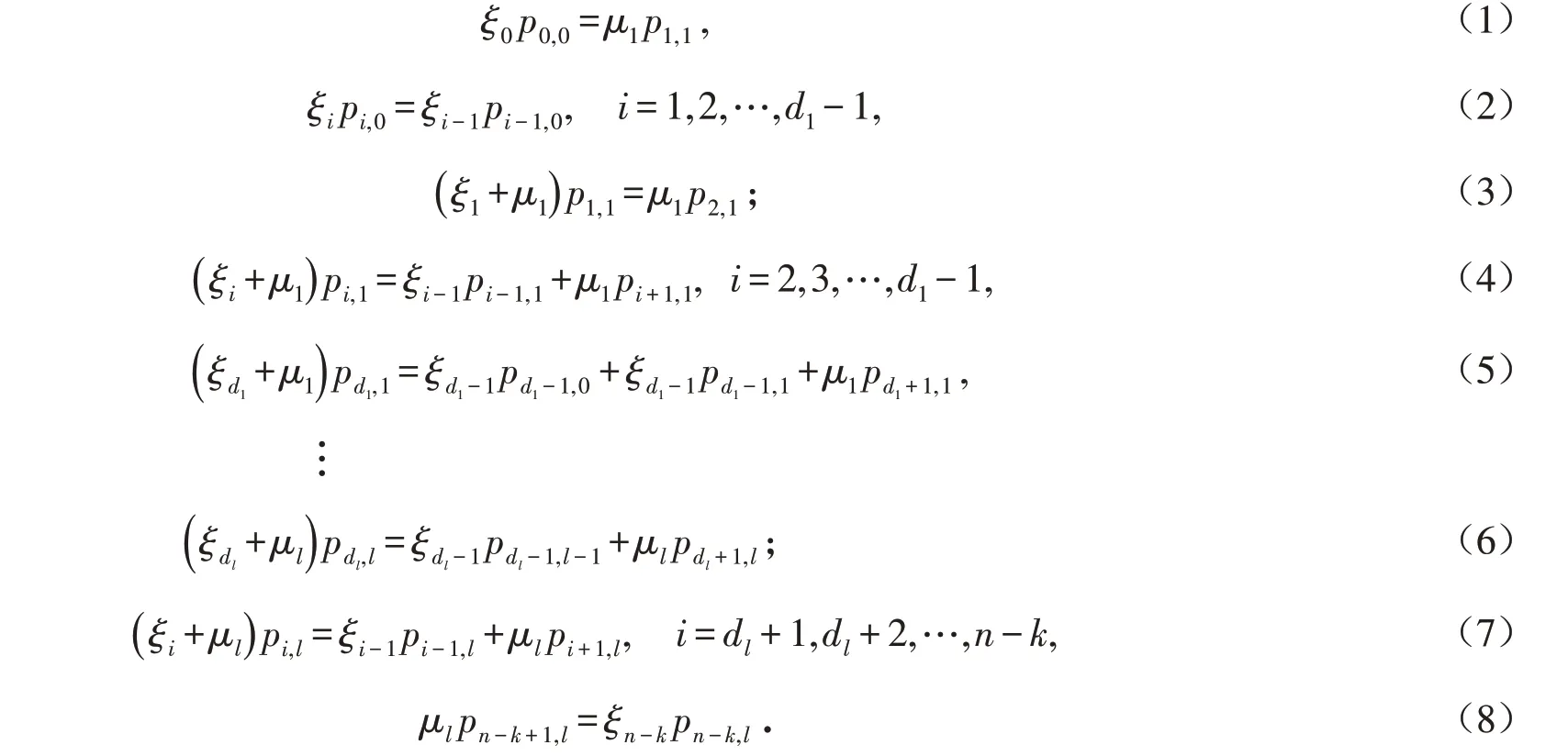
系统模型的求解步骤如下：

步骤1：将上述方程中的pi,j变形为带有p0,0的表达式.

步骤2：根据正则性条件，即式（9），求得p0,0并将其代入步骤1 的pi,j.

步骤3：利用求解出的pi,j推导系统可靠性指标.

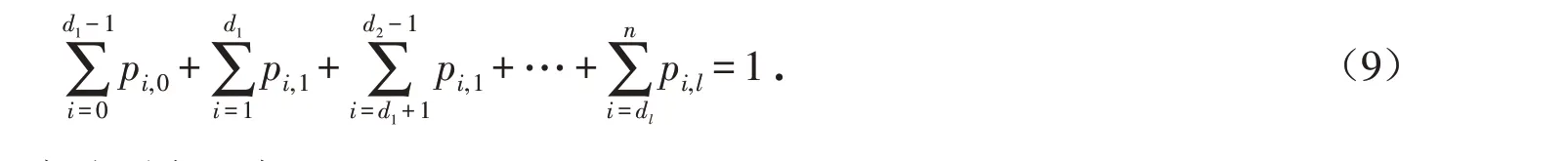
令p0,0=Δ，可得系统稳态概率分别表示为

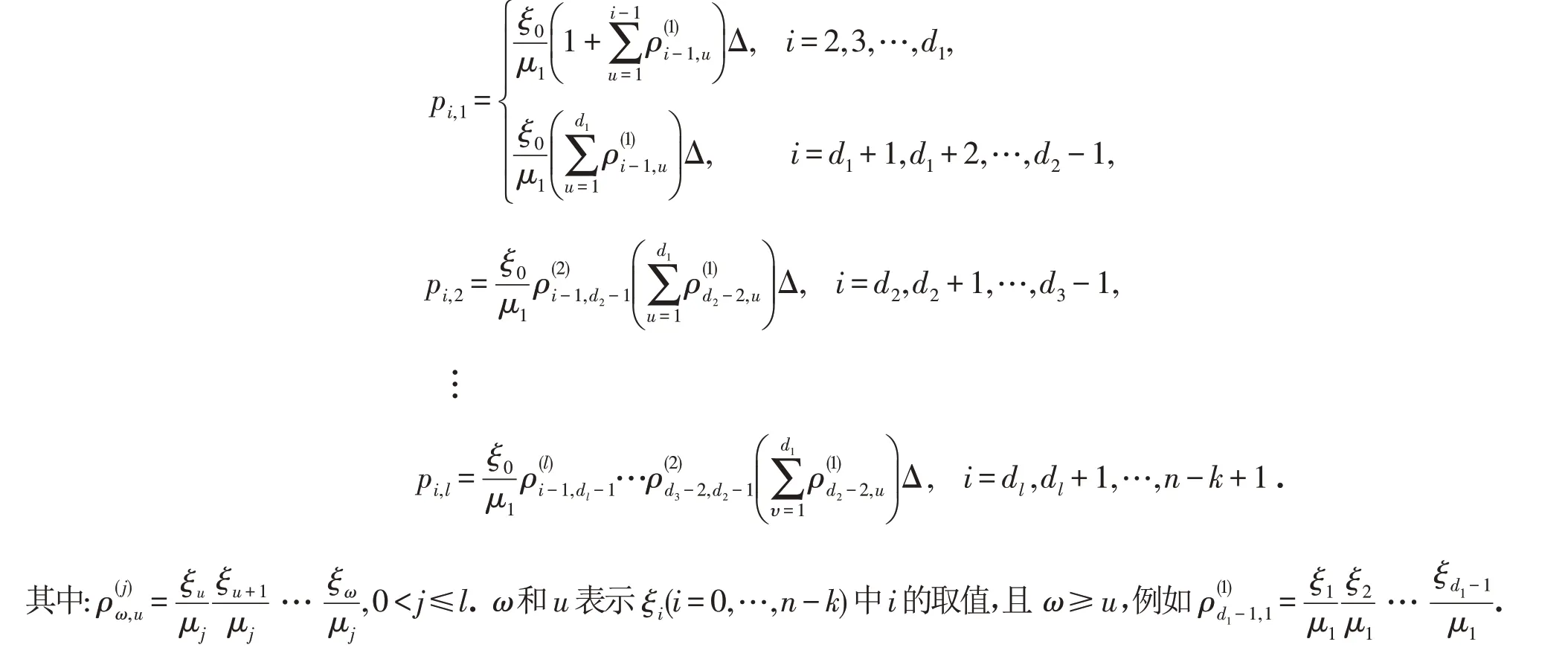
2 系统可靠性指标

1）系统首次故障前平均时间（MTTFF）.

根据Tian和Zhang［15］、曹晋华和程侃［16］的结论，系统中有n-k+d1+1个状态，排列方式为：

令系统故障的状态为过程的吸收态，可得

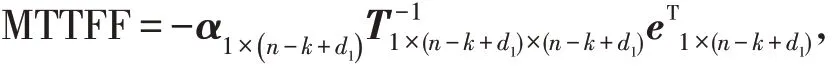
其中：初始概率向量为(α1×(n-k+d1),01×2)，α1×(n-k+d1)=e1×(n-k+d1)(i),i=1,2,…,n-k+d1，e1×(n-k+d1)(i)表示系统以状态i为初始状态时，在向量中对应位置的元素为1，其余位置的元素均为0. 例如，系统以(1,0)为初始状态时，α1×(n-k+d1)=(0,1,0,…,0)1×(n-k+d1).

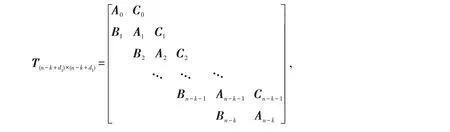
这里：

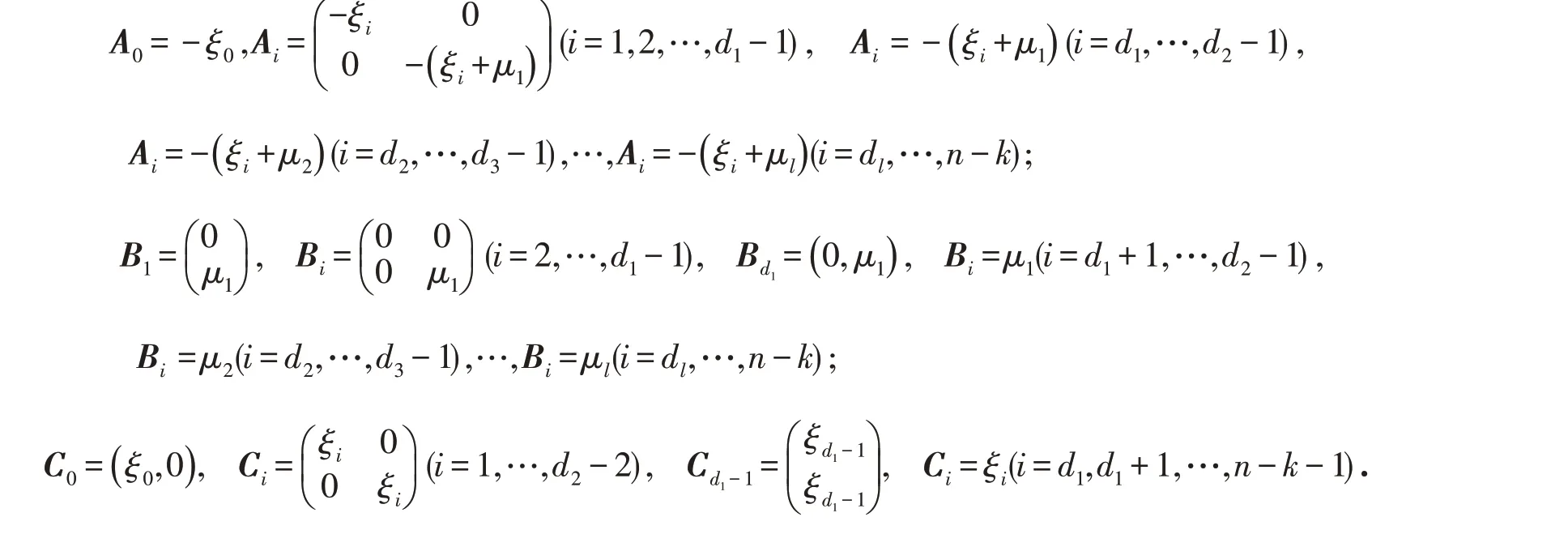
其他可靠性指标如系统平均故障部件数，系统平均停工时间等均可推导得出.

3 优化模型

通过调整多水平(d1,d2,…,dl)修理策略的阈值dj(j=1,2,…,l)，使系统期望成本最小化. 令Cs表示系统预期维修成本，Cdj代表系统在第j个水平的单部件预期维修成本，通常认为Cd1≤Cd2≤…≤Cdl-1≤Cdl，则Cs表示为

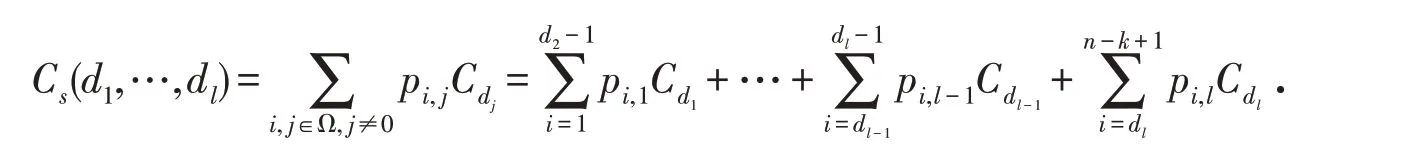
由于系统可用度是评估所提出的维护策略的重要标准，因此，本文以系统可用度作为约束条件，令As表示系统可用度，则As表示为

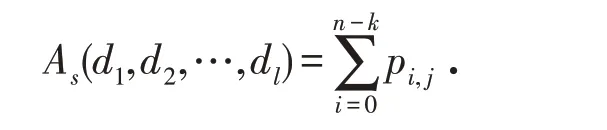
以系统维修成本最小化为目标，以系统可用度为约束条件，令Amin表示系统运行的最小可用度，系统优化模型表示为

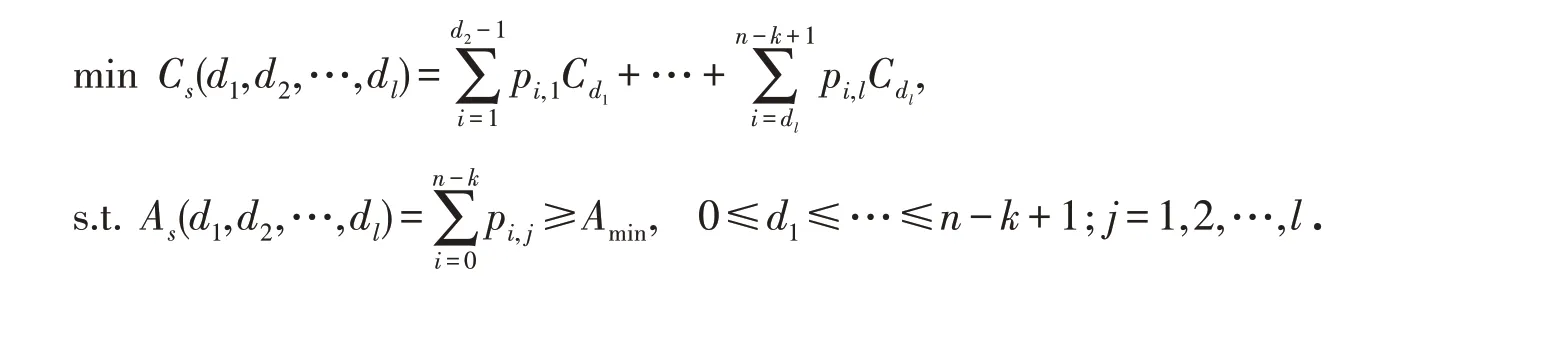
4 数值算例

本节将通过数值算例验证所得研究结果，根据第2节的推导步骤，以一个具有三水平(d1,d2,d3)修理策略的表决系统为例. 假设安装3个传输塔(k=3)就能满足某一区域的通信需求，为了提高通信的质量，管理者现安装13个传输塔(n=13) . 若故障塔的数量小于3个时(d1=3)，不影响该区域的通信；反之，指派一级修理工对故障塔进行修理. 若故障塔的数量持续增加到6个时(d2=6)，指派二级修理工；若故障塔的数量持续增加到9个时(d3=9)，指派三级修理工. 在此期间，传输塔可能受到风力等外部环境的影响，假设外部冲击的v=0.1，p0=0.3，传输塔的工作寿命服从参数为λ的负指数分布，修理工的修理时间分别服从参数为μ1、μ2、μ3的负指数分布. 选取参数独立故障率、各水平维修率以及系统运行的最小可用度分别为λ=0.2，μ1=1.2，μ2=1.5，μ3=2.0，Amin=0.95，单部件预期维修成本为Cd1=100，Cd2=200，Cd3=300，相关结果保留至小数点后10位.

表1和表2分别给出了系统稳态概率分布pi,j、系统稳态可用度A、系统稳态故障频度M、各水平修理工修理部件的概率等可靠性指标以及不同初始条件下系统首次故障前的平均时间的数值结果. 从表2中可以看出，系统在初始时刻的故障部件越多，其首次故障前的平均时间就越小，这符合实际情形.

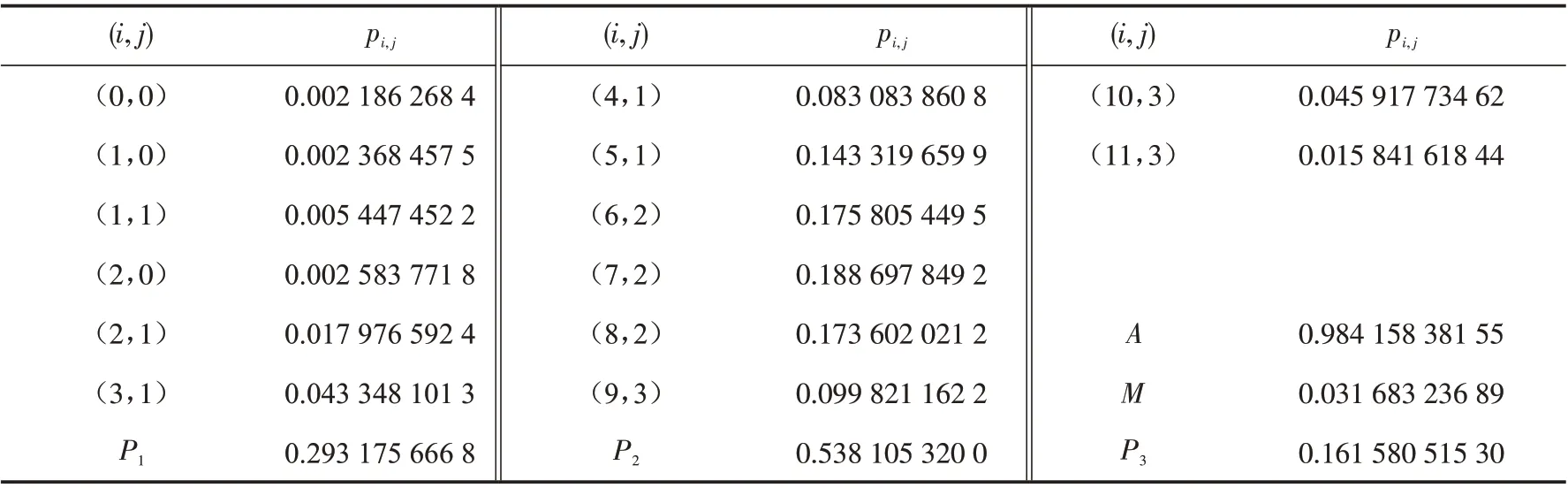
表1 3/13(G)表决可修系统稳态概率分布的数值结果Tab.1 Numerical results of the steady-state probability distribution of the system 3/13(G)

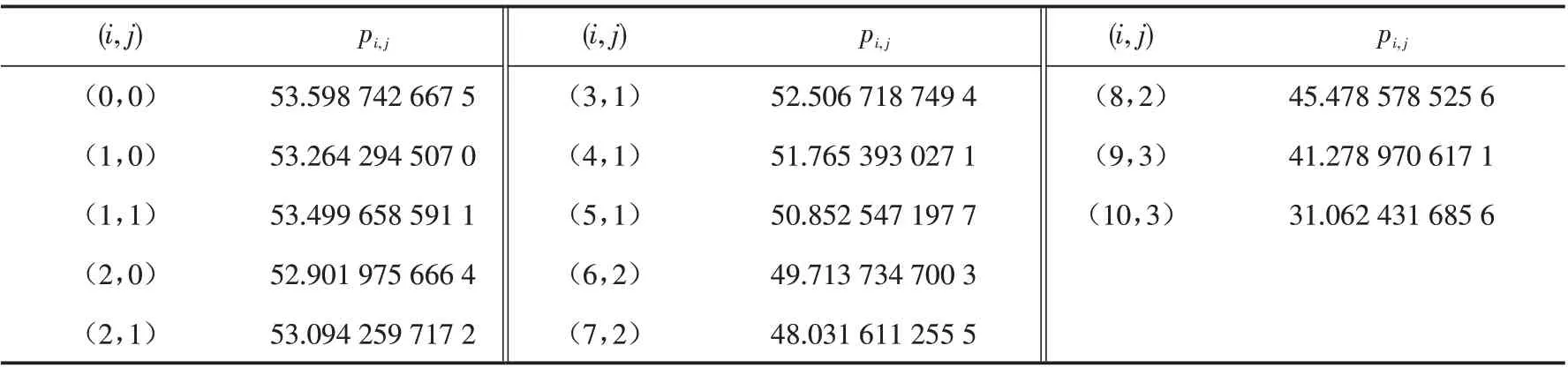
表2 不同初始条件下3/13(G)表决可修系统首次故障前平均时间Tab.2 MTTFF of the system 3/13(G)under different initial conditions

首先，为了说明部件的竞争失效对系统可靠性的影响，系统可用度A和故障频度M在不同故障率下的变化趋势如图3所示. 可以看出，随着部件独立故障率λ的增大，系统可用度A不断减小，故障频度也随之升高；当给定λ时，冲击速率v越大，系统可用度越小，而故障频度越大. 这是因为部件由于内部原因或外部冲击而发生故障，导致系统可用度降低.

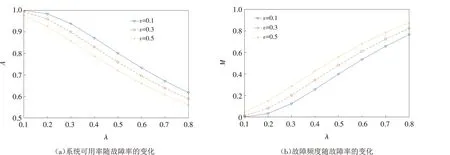
图3 不同故障率下系统可靠性指标的变化趋势Fig.3 Change trends of system reliability indexes under different failure rates

其次，不同维修阈值对系统期望维修成本的影响如表3所示，最小系统预期维修成本为172.32. 可以看出，二级修理工进入系统的时间越晚，系统预期维修成本越小，但系统可用度越低，因此需要根据实际情况调整维修策略.

表3 不同维修阈值下系统的期望成本Tab.3 Expected costs of the system under different maintenance thresholds

5 结论

本文针对k/n(G)表决可修系统，考虑多水平修理策略对维修成本的影响. 利用马尔可夫分析方法建立了系统模型，推导了系统可用度、首次故障前平均时间等可靠性指标，并建立维修成本优化模型，最后以三水平修理策略为例验证了研究结果的实用性. 结果表明，多水平修理策略更符合实际情况对各级修理工的不同需求，对系统维修成本的优化问题也有很大的影响.