疫情影响下贵金属市场的波动性——基于厚尾SV模型的实证研究

高博文， 乔克林

（延安大学数学与计算机科学学院，陕西延安 716000）

贵金属的产品主要有黄金、白银、铂金等，其中黄金和白银最为出名，且贵金属的保值、收藏、投资受到了广大贵金属爱好者的青睐. 贵金属的投资在国内起步较晚，然而却依然引来了全国广大投资者的喜爱，为投资者多了一个投资渠道，并且使全国的金融大市场得到了有效的完善. 当出现金融危机、政局动乱以及疫情影响，贵金属的经济价值就会体现出来，具有非常好的抗压、保值能力，因此，研究贵金属的收益波动是非常有意义的一件事情.

在SV模型的研究方面，从刚开始的标准SV模型到SV-T模型、杠杆SV模型、跳跃的SV模型等，其目的都是为了更好地刻画波动率特征. 在研究SV 模型的同时又深入地研究了参数估计中的一些方法，主要有MM估计法、GMM估计法、QML估计法和MCMC参数估计等方法. MM估计法也称矩估计法，最早是由Taylor提出来的，也是最为简便的一种方法；GMM估计法也称广义矩估计法，是由Hansen提出来的，其思想是依照矩条件在弱假设下进行估计，因此它可以说是矩估计法的一个推广；Melino 等［1］最先将GMM估计法应用在SV模型的参数估计上；QML估计法也称伪极大似然估计法，最早是由Harvey等［2］提出来的；MCMC参数估计法也称马尔科夫链蒙特卡洛算法，最早是由Sandmann等提出来的；Jacquier等［3］是第一个将SV模型中引入了贝叶斯分析，并且运用MCMC方法来进行参数估计.

自1986年随机波动模型被首次提出至今，研究者不断地对其进行拓展研究，其金融时间波动模型的SV模型族也在我国研究范围甚广，其中包括李峰［4］在对我国股市的研究中利用标准SV模型和SV-T模型、SV-GED模型、SV-MN模型、SV-MT模型进行了对比分析，最后得出尖峰厚尾现象也是普遍并且明显地存在于我国的股市市场，而且SV-T模型在对我国股市的收益率模拟中效果最优；朱慧明等［5］在描述金融时间序列的尖峰厚尾性中采用了SV-T模型，结果表示SV-T模型可以更好地反映出金融市场尖峰厚尾的特性；于冉春［6］同样使用标准SV模型和SV-T模型对普尔500股票指数的收益率进行对比研究，最后得到SV-T模型具有更好的拟合效果. 赵行为［7］运用了标准SV模型以及SV-T模型对中国银行和交通银行的收益序列进行了模型的对比分析，最后得出SV-T模型对两家银行收益的波动率以及拟合结果更准确于标准SV模型；张艳慧等［8］利用SV-N模型和SV-T模型实证分析了中国股市高频数据收益率的波动性具有尖峰厚尾、聚集性等特征；杨超等［9］构建SV-N模型和SV-T模型，并利用MCMC方法求解模型参数并对比了模型的拟合效果，最后发现在刻画波动率的波动特征效果上，SV-T模型要优于SV-N模型. 郭建峰和白瑜瑜［10］通过对科技创板指数进行实证研究，采用SV-N 模型和SV-T 模型来研究科技创板的波动性，结果表明，科创板指数收益率波动较大且持续时间较长，且SV-T模型的拟合效果明显优于SV-N模型.

考虑到厚尾性在金融时间序列中的普遍存在及其表现形式，该文使用厚尾SV模型来研究贝叶斯参数估计，并对疫情前和疫情期间我国贵金属的收益波动性进行实证分析.

1 厚尾随机波动模型

在解释金融时间收益序列波动模型的自回归行为时，在标准SV模型的基础上提出了厚尾SV模型，其数学解析式如下：

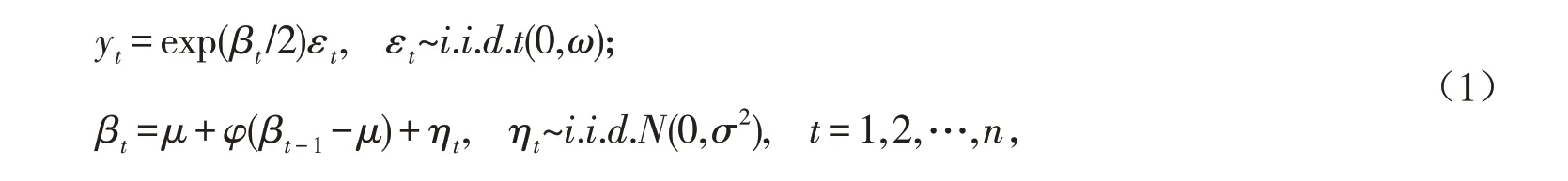
其中：yt表示t时刻资产对数收益率；εt为扰动项且是服从自由度为ω的t分布，并且是服从方差为σ2，均值为0的正态分布；βt代表对数波动率；μ表示平均波动水平；ηt可以衡量波动的扰动水平，且εt与ηt互不相关；φ为持续性参数，反映目前的波动状态对未来波动状态的影响.

厚尾SV模型中为了方便记τ=1/σ2，其反映收益波动的扰动水平；记y=(y1,y2,y3,…,yn)，β=(β1,β2,β3,…,βn)，未知参数θ=(μ,φ,ω,τ) .

厚尾模型中，εt服从t分布，ηt服从正态分布. 则假设βt-1和θ一定的情况下βt服从以下分布：

则ηt关于(βt-1，θ)的概率密度函数为：

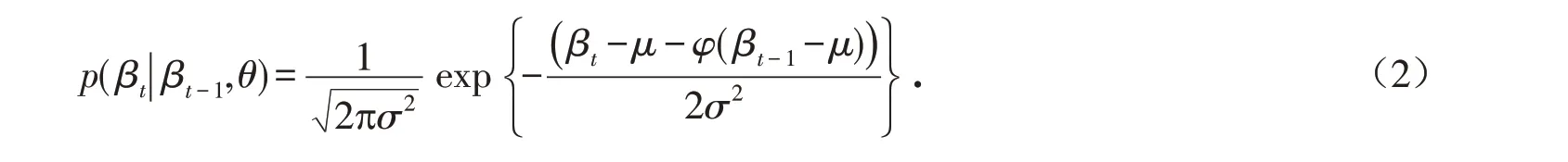
εt的概率密度函数为：

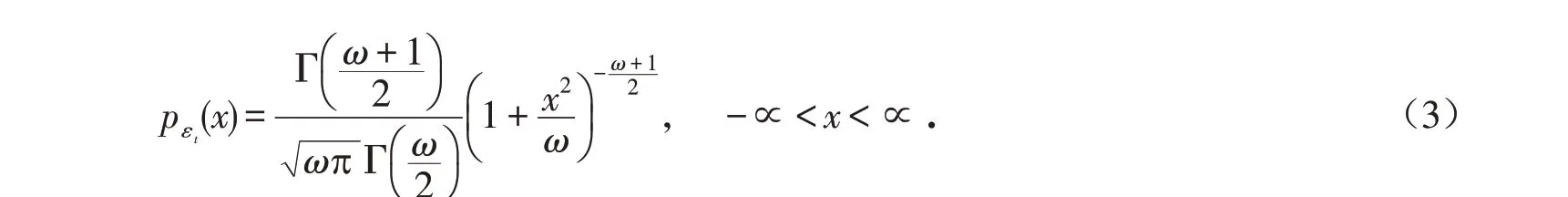
对数收益率yt的概率密度函数为：

2 厚尾SV模型的后验分布及Gibbs抽样

2.1 SV-T模型的后验分布

贝叶斯推断中，参数先验分布的设定是必须的.μ、φ、ω、τ 和波动率β是标准SV模型中的未知参数，且参数φ的取值范围已经是限定的，所以设φ=2φ1-1. 根据Kim等［11］的观点我们得知参数μ、φ、τ 和β0的先验分布为：

再根据Meyer和Ju［12］设定好的未知参数ω的先验分布：

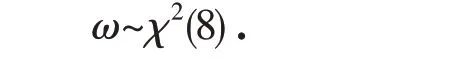
以下是厚尾SV模型各个参数的后验条件分布密度函数.

1）厚尾SV模型中参数μ的后验条件分布：

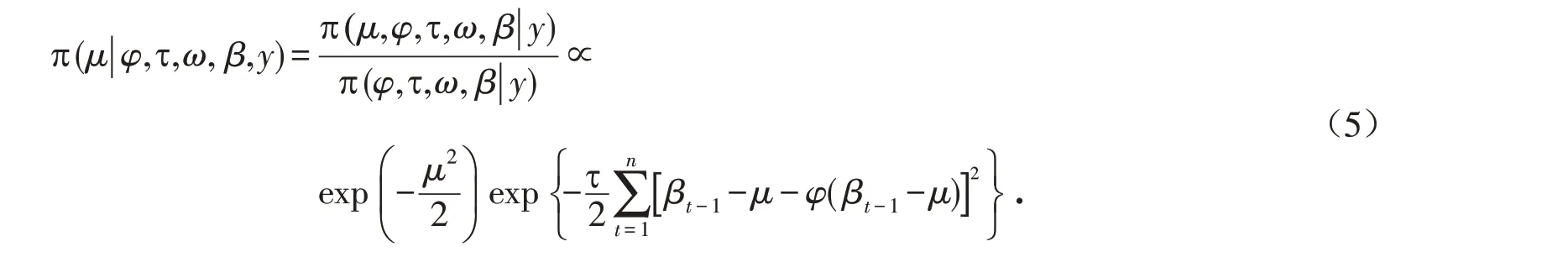
2）厚尾SV模型中参数φ的后验条件分布：

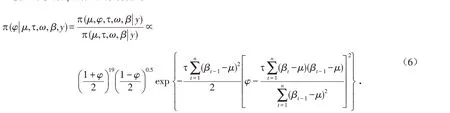
3）厚尾SV模型中参数τ 的后验条件分布：

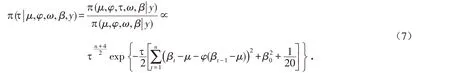
4）厚尾SV模型中参数ω的后验条件分布：

5）厚尾SV模型中参数βt的后验条件分布：

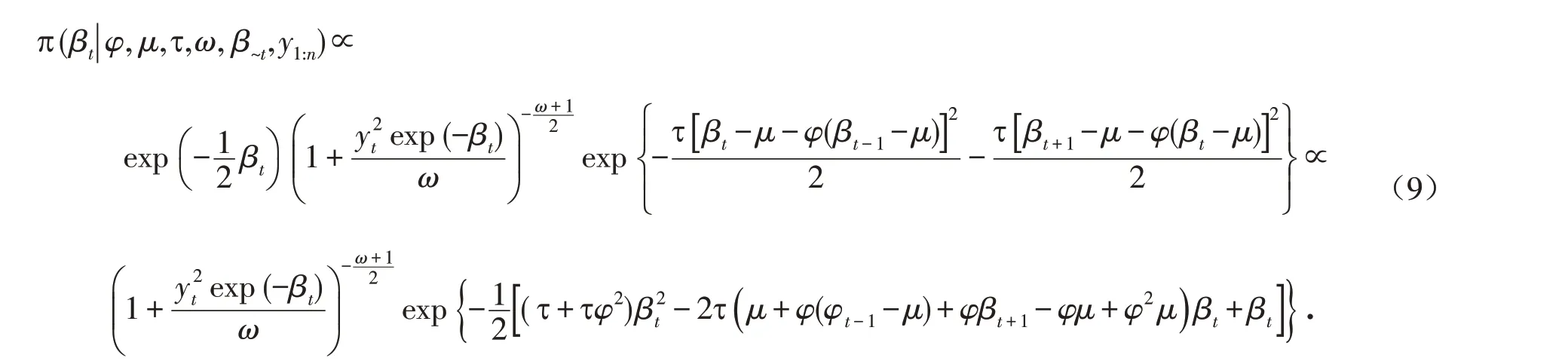
2.2 Gibbs抽样

MCMC 方法中最常用的是Gibbs 抽样法［13］，在厚尾SV模型中记未知参数θ0=(μ,φ,ω,τ,βt），则初始值为

3 实证分析

3.1 数据预处理与数据特征

自2019年12月31日湖北省武汉市卫健委首次公开通报新型冠状病毒肺炎病例以来，疫情一直持续至今. 基于此，本文选取2018年1月1日至2019年12月31日共计487个日收益率以及2020年1月1日至2022年1月5日共计488个日收益率来研究在疫情前和疫情期间我国贵金属的收益波动情况，并作为我们的建模样本. 在本文SV模型中采用的收益率为去均值化后的收益率，且定义公式Rt=ln(Ft)-ln(Ft-1)，则

其中：yt代表收益率；Ft代表黄金收盘价第t日的交易价格；n代表样本数.

用SPSS软件［15］对疫情前和疫情期黄金的收益率进行统计分析得出黄金收益序列的正态Q-Q图以及正态概率无趋势图，如图1、图2所示.

由图1中黄金收益序列的正态Q-Q图可以看出疫情前和疫情期黄金的收益率分布偏离了直线，所以可以说呈现出明显的厚尾状态. 从图2正态概率分布图中我们可以发现数据与正态的偏差是显而易见的.

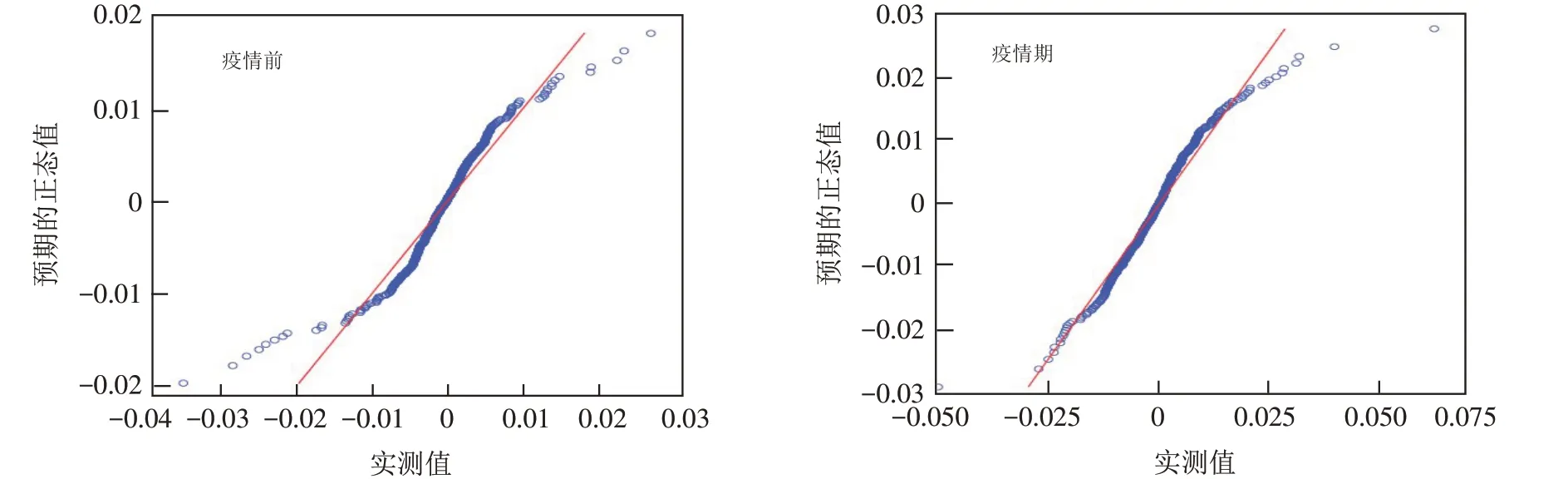
图1 黄金收益序列的正态Q-Q图Fig.1 Normal Q-Q diagrams of gold return series

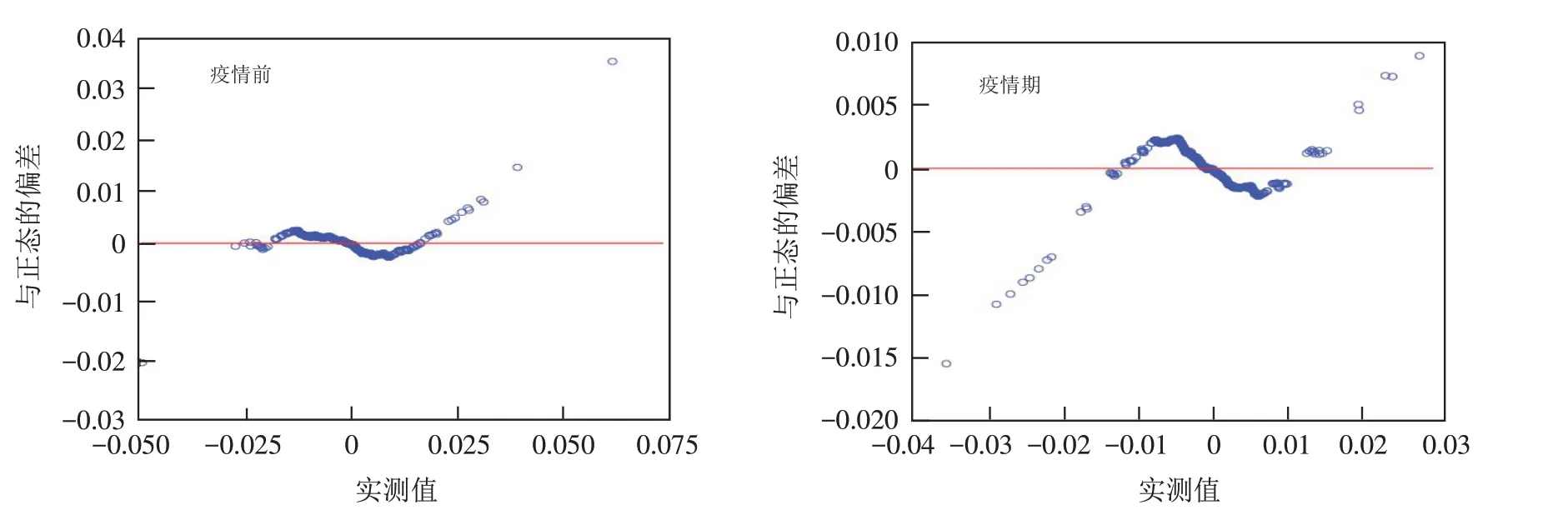
图2 黄金收益序列的正态概率无趋势图Fig.2 No trend charts of normal probabilities of gold return series

最后我们依然使用SPSS 软件对疫情前和疫情期黄金收益率的基本指标进行统计分析，分析结果如表1所示.

表1 统计结果表Tab.1 Statistical results

由表1我们可以发现疫情前黄金的平均值较小可忽略不计，所以表示为0.00. 中位数为-0.000 86，方差同样较小可忽略不计，表示为0.00. 标准差为0.062 68，偏度为-0.529，峰度为5.504，其中峰度5.504大于正态分布的峰度（=3），可以看出疫情前黄金的收益率具有明显的峰度，比正态分布的峰度大2.504，所以呈现出来了很强的厚尾性.

同样由表1 我们可以发现疫情期黄金收益率的平均值较小，依然表示为0.00. 中位数为-0.000 35，方差也较小，表示为0.00. 标准差为0.095 93，偏度为0.630，峰度为5.756，其中峰度5.756 大于正态分布的峰度（=3），因此可以看出疫情期黄金的收益率也具有非常明显的峰度，比正态分布的峰度大2.756，所以依然呈现出来了很强的厚尾性.

3.2 SV-T模型的参数估计

我们使用WinBUGS软件以及运用基于MCMC方法的贝叶斯方法进行参数估计，其中的抽样方法我们选择Gibbs抽样，为了使参数稳定以及收敛，我们首先对参数进行了10 000次的迭代，然后进行退火，再对参数进行第二次迭代，第二次的迭代次数为30 000次，最后得到了参数μ、φ、τ、ω的参数估计结果.

3.2.1 疫情前SV-T模型的参数估计

表2是疫情前SV-T模型各参数的估计结果.

表2 参数估计结果表Tab.2 Parameter estimation results

通过表2的参数统计结果，我们可以得到以下结论.

1）参数μ的均值为-11.13，相当于参数μ的贝叶斯估计值为-11.13，因此可以看出我国黄金市场的风险较低，有利于投资者的进一步投资，且可以看出参数μ的标准差为0.397 9. MC误差为0.016 51，MC误差越接近0表示参数估计的值越精确. 2.5%分位数为-12.01，97.5%分位数为-10.42，因此参数μ的置信区间为（-12.01，-10.42）.

2）参数φ的均值为0.990 4，即参数φ的贝叶斯估计值为0.990 4，且参数φ的标准差为0.006 67. MC误差为3.393×10-4. 2.5%分位数为0.972 8，97.5%分位数为0.998 7，因此置信区间为（0.972 8，0.998 7）. 由于参数φ代表模型的波动持续参数，所以可以看出我国黄金市场展现出了强的波动持续性.

3）参数τ 的均值为47.81，即参数τ 的贝叶斯估计值为47.81，且参数τ 的标准差为29.47. MC 误差为1.955，2.5%分位数为12.36，97.5%分位数为121.7，因此置信区间为（12.36，121.7）. 由前面的假设值知τ=1/σ2，所以看出参数τ 与σ2成反比，且随着σ2的变化而变化.

4）参数ω的均值为7.655，即参数ω的贝叶斯估计值为7.655，且参数ω的标准差为2.385，MC 误差为0.118 2，2.5%分位数为4.378，97.5%分位数为13.59，所以置信区间为（4.378，13.59），因此更可以看出我国黄金市场波动率尖峰厚尾的特点.

综上所述，可以确定SV-T模型为：

然后我们继续用WinBUGS软件对参数进行分析，得到了厚尾SV模型的后验分布仿真图、参数的迭代轨迹图和参数的迭代历史图，其中omega=ω，phi=φ，mu=μ，itau=τ . 如图3～5所示.

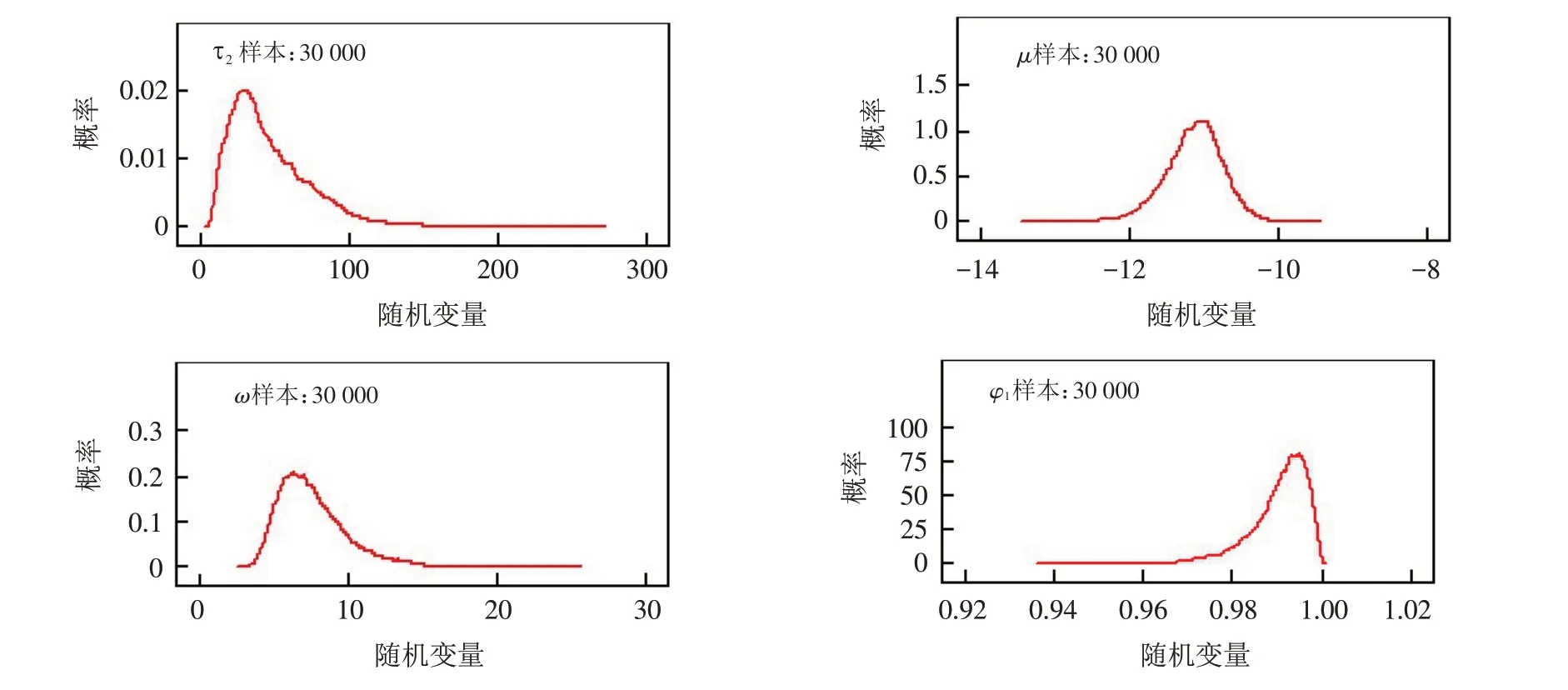
图3 参数后验分布仿真图Fig.3 Simulation diagrams of posterior distributions of parameters

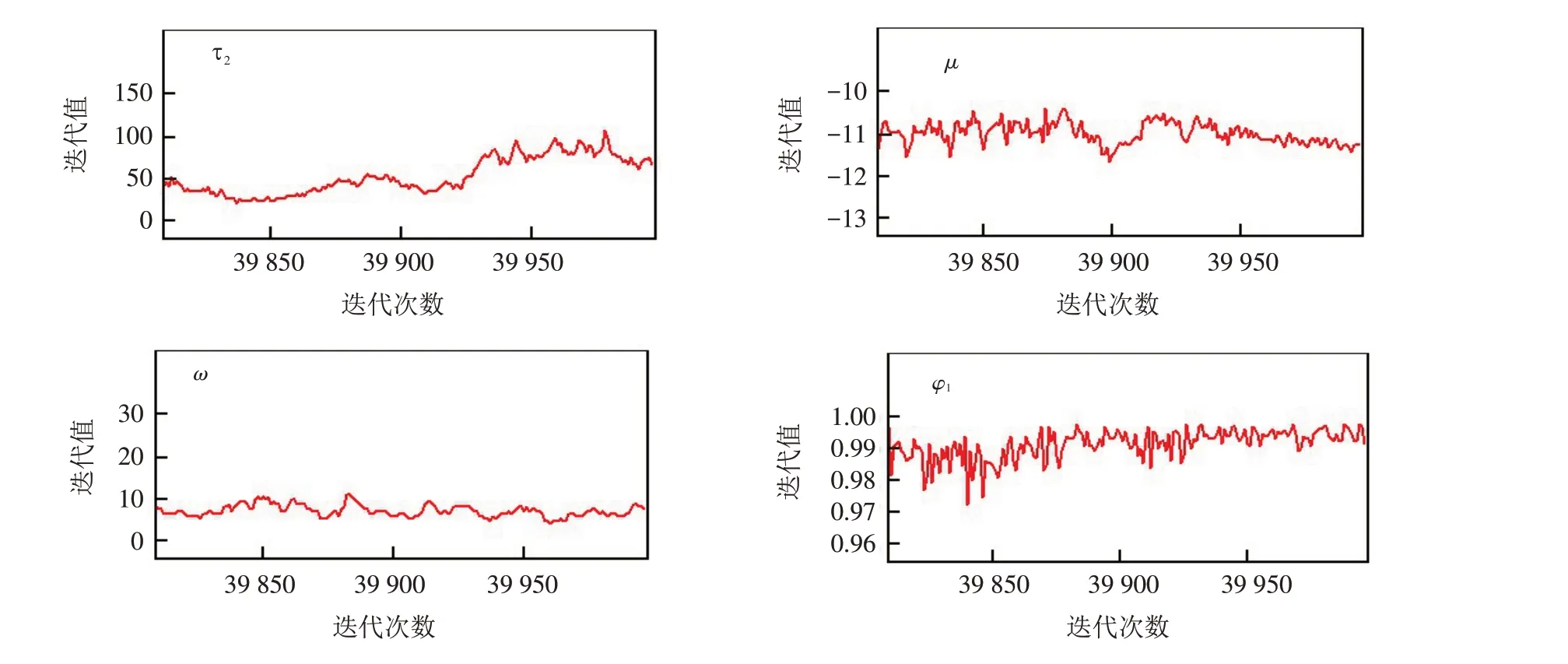
图4 参数迭代轨迹图Fig.4 Parameter iteration trajectory diagrams

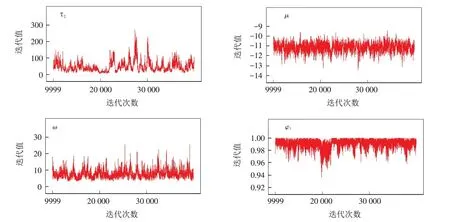
图5 参数迭代历史图Fig.5 Parameter iteration history diagrams

3.2.2 疫情期SV-T模型的参数估计

表3是疫情期SV-T模型各参数的估计结果.

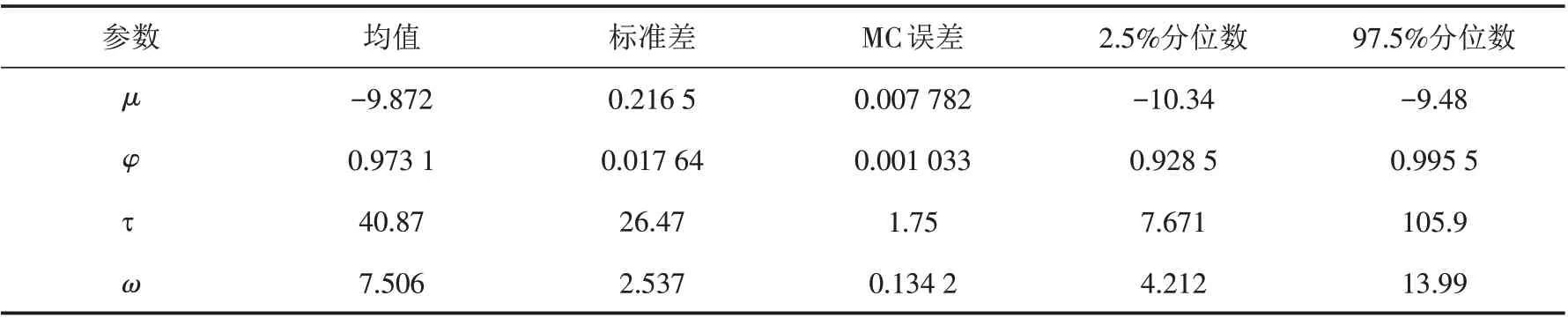
表3 参数估计结果表Tab.3 Parameter estimation results

通过表3的参数统计结果，我们可以得到以下结论.

1）参数μ的均值为-9.872，相当于参数μ的贝叶斯估计值为-9.872，因此可以看出我国黄金市场的风险较低，有利于投资者的进一步投资，且可以看出参数μ的标准差为0.216 5. MC 误差为0.007 782，MC 误差越接近0 表示参数估计的值越精确. 2.5%分位数为-10.34，97.5%分位数为-9.48，因此参数μ的置信区间为（-10.34，-9.48）.

2）参数φ的均值为0.973 1，即参数φ的贝叶斯估计值为0.973 1，且参数φ的标准差为0.017 64. MC误差为0.001 033，置信区间为（0.928 5，0.995 5）. 因为参数φ代表模型的波动持续参数，所以可以看出我国黄金市场展现出了强的波动持续性.

3）参数τ 的均值为40.87，即参数τ 的贝叶斯估计值为40.87，且参数τ 的标准差为26.47. MC 误差为1.75，置信区间为（7.671，105.9）. 由前面的假设值知τ=1/σ2，所以看出参数τ 与σ2成反比，且随着σ2的变化而变化.

4）参数ω的均值为7.506，即参数ω的贝叶斯估计值为7.506，且参数ω的标准差为2.537. MC 误差为0.134 2，置信区间为（4.212，13.99），因此更可以看出我国黄金市场波动率尖峰厚尾的特点.

综上所述，可以确定SV-T模型为：

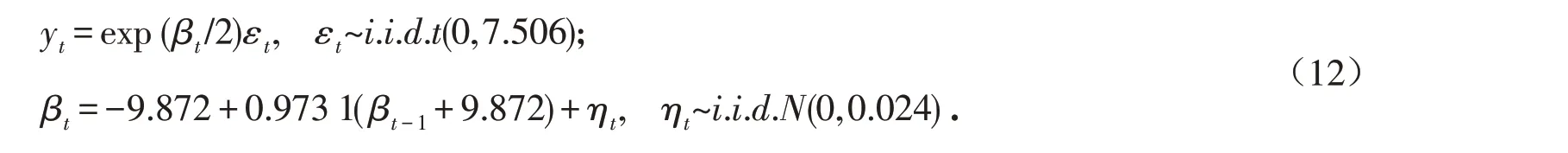
然后我们继续用WinBUGS软件对参数进行分析，得到了厚尾SV模型的后验分布仿真图，参数的迭代轨迹图和参数的迭代历史图，其中omega=ω，phi=φ，mu=μ，itau=τ . 如图6～8所示.

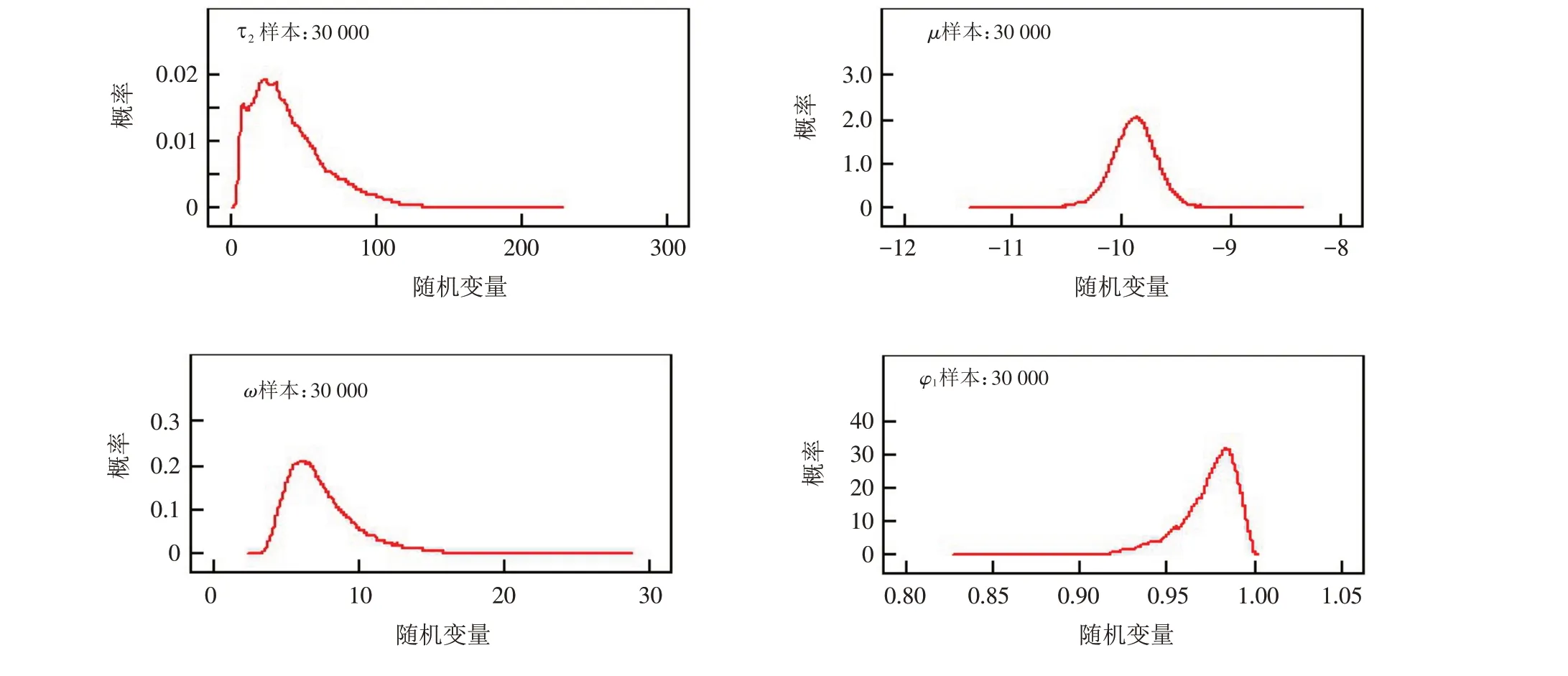
图6 参数后验分布仿真图Fig.6 Simulation diagrams of posterior distributions of parameters

3.3 疫情前和疫情期参数模拟结果对比分析

通过疫情前和疫情期两个不同时间段对SV-T模型各参数的估计，我们进行了对比，结果如表4.

对表4进行对比分析得到以下结论.

表4 参数估计结果对比Ta.4 Comparison of parameter estimation results

1）疫情前参数μ的值为-11.13，疫情期参数μ的值为-9.872，即疫情前参数的贝叶斯估计值小于疫情期的贝叶斯估计值. 参数μ的绝对值越小则体现出黄金市场的风险越低，因此我们看出在疫情前投资贵金属的风险性是要高于疫情期的，所以我们可以看出，疫情对贵金属投资爱好者来说是有一定的影响的，也体现了投资贵金属市场的不确定性.

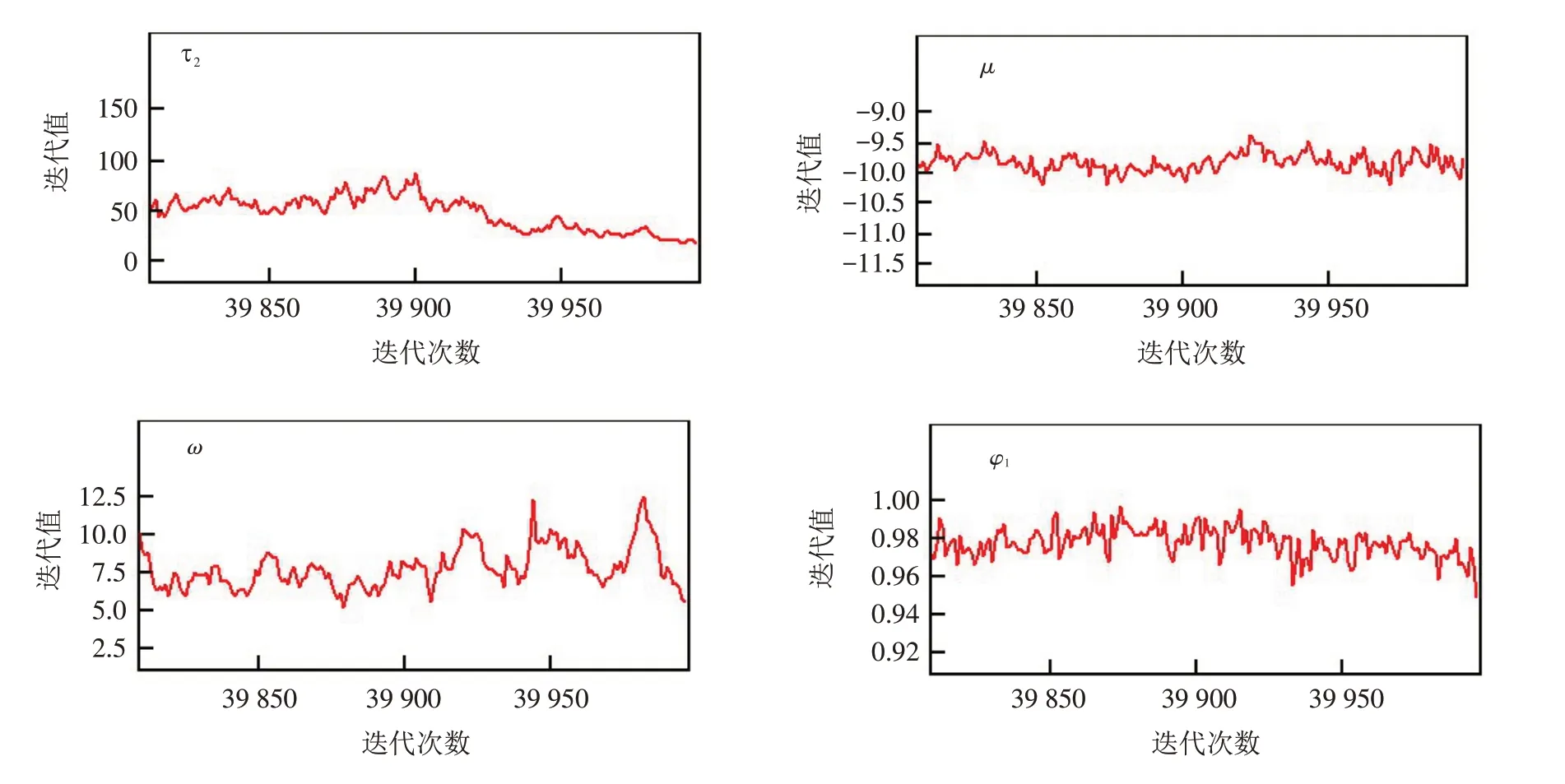
图7 参数迭代轨迹图Fig.7 Parameter iteration trajectory diagrams

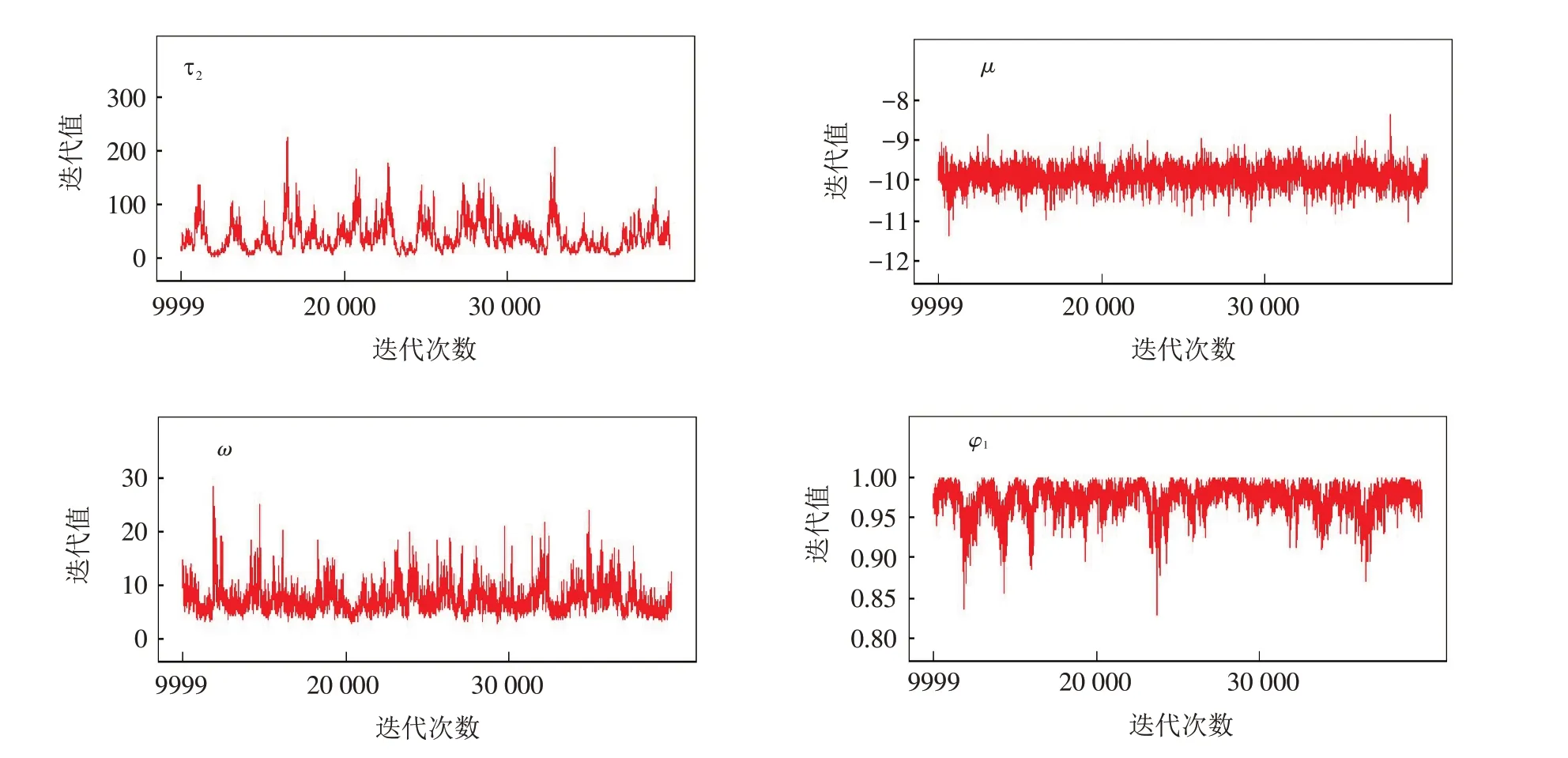
图8 参数迭代历史图Fig.8 Parameter iteration history diagrams

2）疫情前参数φ的值为0.990 4，疫情期参数φ的值为0.973 1，二者均小于1，因此比较平稳.φ代表了模型的波动持续参数，不难看出我国贵金属市场具有强的波动持续性，而且可以看出在疫情前的波动性要强于疫情期间的波动性.

3）疫情前参数τ 的值为47.81，疫情期参数τ 的值为40.87，参数τ 可以衡量黄金收益率波动的扰动水平，因为τ=1/σ2且参数σ代表波动的扰动水平，即参数τ 的值越小则参数σ的扰动水平越强，所以可以得到疫情期黄金收益的波动扰动水平要强于疫情前黄金收益的波动扰动水平.

4）疫情前参数ω的值为7.655，疫情期参数ω的值为7.506，参数ω代表了自由度，因为疫情前和疫情期的自由度均小于8，因此可以体现出贵金属市场尖峰厚尾的特性. 又因为7.755＞7.506，所以在疫情前的尖峰厚尾性要略强于疫情期，疫情前所呈现的尖峰厚尾性更加明显.

4 结论

本文主要研究了基于厚尾SV模型的贝叶斯参数估计，研究对象为我国贵金属市场里黄金的收益率，并挑选疫情前和疫情期的时间序列来进行对比研究. 实证分析中，对模型的参数估计使用的是MCMC 方法，并结合了贝叶斯估计法，然后使用的抽样方法为Gibbs抽样方法，利用WinBUGS软件进行了详细的分析，最终又将疫情前和疫情期参数模拟结果进行了对比分析，结果表明SV-T模型在疫情前和疫情期对我国贵金属收益的波动性都具有准确并且较好的拟合效果.