基于最小二乘法的电容式电池均衡系统研究*

管 宇 ， 李 乾 ， 陈文兴

（柳州工学院汽车工程学院，广西 柳州 545616）

0 引言

温室效应、能源紧缺等一系列问题威胁着传统汽车产业的可持续发展，新能源汽车是解决这些问题的重要手段。电池汽车作为新能源汽车的典型代表，采用动力电池作为整车动力来源，是整车的核心[1]。电动汽车的安全性、动力性取决于动力电池的性能，而锂离子电池具有输出功率大、不存在记忆效应、重量轻等优点，广泛应用于目前的电动汽车中[2]。但锂离子电池在制造过程中还存在着一些尚未解决的问题，其中电池的不一致性问题对整车的续航里程、安全性能等指标影响最大，在电池组长期使用过程中，其不一致性会逐渐恶化，电池的容量、电压等参数会变得愈加不理想，并且这种现象是不可逆的。因此，对电池进行均衡管理是必要的，而电容式主动均衡由于能量利用率高、均衡速度快，已成为国内外电动汽车均衡技术的研究热点。

1 均衡系统电路结构与工作过程

1.1 均衡电路结构

均衡方案主要分为主动均衡与被动均衡两类。被动均衡指将单体电池中的能量转化为热能消耗掉；主动均衡指通过能量转移载体进行能量的转移，根据能量转移的中间载体不同，主动均衡主要分为电容式、电感式、变换器式三类[3]。以电容式均衡系统为例进行研究，设计出以电容为中间储能单元的电路模型。该电路模型以两个单体电池B1、B2构成一个模块，MOSFET晶体管M1、M2、M3、M4是均衡控制元件，通过MOSFET管控制相邻两个单体电池之间的能量均衡。

1.2 能量均衡工作过程

电容“充电”过程：电压传感器实时检测单体电池B1、B2的电压U1、U2，并将电压信号传至均衡控制中心，控制中心根据此信号判断是否开启或断开均衡电路。假设B1的内阻R1大于B2的内阻R2，则B1的电压率先达到极限值，若U1、U2的差值达到均衡开启的阈值，则晶体管的M1、M3的栅极G收到触发信号后导通，此时电池B1、电容C1、晶体管M1、M3构成回路，电容C1将电池B1的电能转换为电场能储存起来，充电过程结束后M1、M3截止，电容C1的充电过程完成。如图1所示。

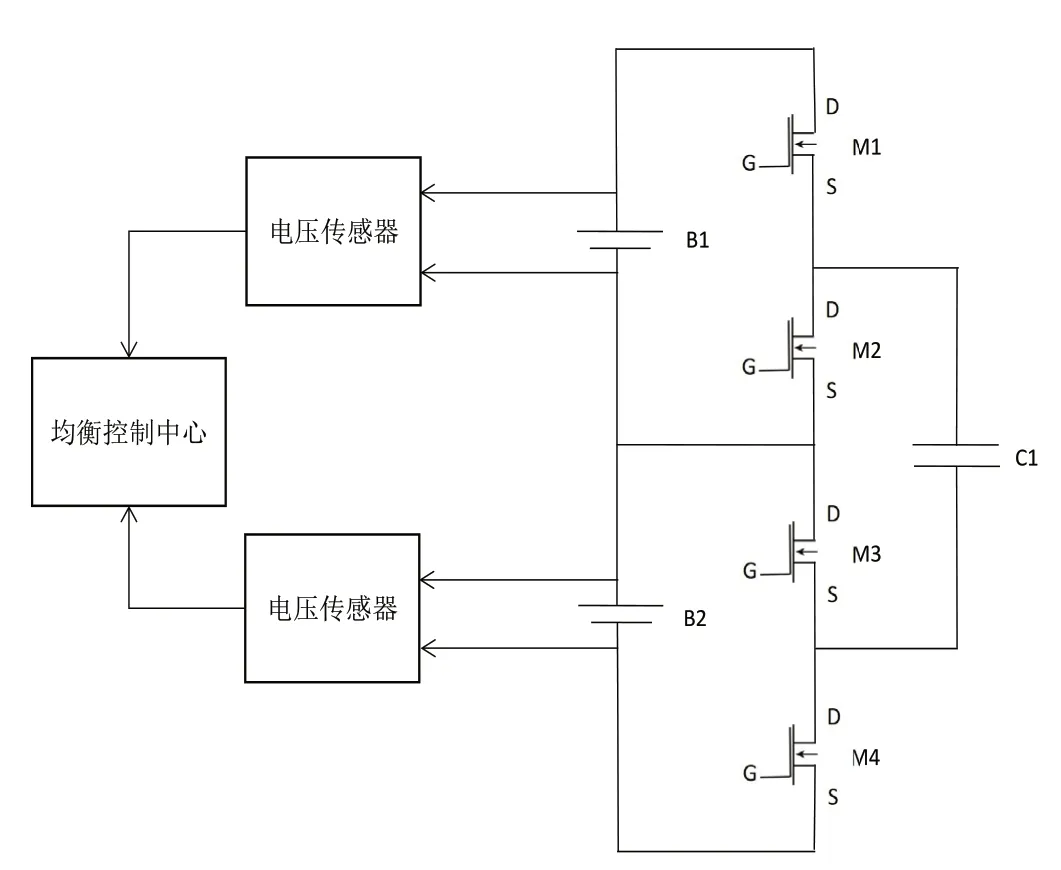
图1 电容式均衡电路模型

电容“放电”过程：若U1、U2的差值达到均衡开启的阈值，均衡电路开启，能量转移原理与电容“充电”过程相同，即M2、M4导通，电池B2、电容C1、晶体管M2、M4构成回路，此时储存在电容中的电场能转换为电能对B2进行充电，充电完成后，M2、M4截止。完成这个过程后，实现电池B1和B2之间的能量传递。

2 均衡系统能量转移数学模型分析

2.1 高能量单体电池给中间储能载体转移能量

选择以电容作为能量转移的中间载体，均衡过程分为电容充电、放电两个过程。

设U1表示电池单元B1的初始端电压，uC1表示电容C1的端电压，R1为电路模型总内阻，根据KVL，充电到t时刻电压平衡方程为：

高能量单体电池给电容转移能量过程的微分方程为：

2.2 中间储载单元给低能量单体电池转移能量

在电容放电过程，电容C1向单体电池B2充电。设U2表示电池单元B2的初始端电压，R2表示电路模型的总内阻，uC1表示电容C1的端电压，根据KVL，充电到t时刻的回路电压平衡方程为：

电容给低能量单体电池转移能量过程的微分方程为：

2.3 均衡系统传递函数

设式（2）中uC1、U1对应的象函数分别为C(s)、F(s)，微分算子用复变量s表示，在零初始条件下对式（2）进行拉普拉斯变换得到电容C1在充电过程的传递函数为：

设式（4）中uC1、U2对应的象函数分别为C(s)、F(s)，微分算子用复变量s表示，在零初始条件下对式（4）进行拉普拉斯变换得到电容C1在放电过程的传递函数为：

3 系统时域分析

通过对系统进行时域分析，可根据系统输出量直观、准确地分析系统的暂态和稳态性能[4]。

3.1 一阶系统时域分析

一阶系统传递函数的标准形式为：

式中，T为时间常数，当系统输入信号为单位阶跃信号，即r(t)=1(t)，并进行拉普拉斯逆变换，得一阶系统的单位阶跃响应为：

时间常数T越小，系统阶跃响应越快[5]。因此，取时间常数T=1对均衡系统进行时域分析。

3.2 均衡系统时域分析

为提高均衡系统输入信号的可靠性，以相邻两电池电压差作为均衡目标，使用最小二乘法对均衡系统进行时域拟配，求取系统阶跃响应曲线，研究系统输出量随时间的变化关系[6]。

3.2.1 电容充电过程的时域分析

由式（5）可知，电容在充电过程系统的传递函数为：

在仿真软件系统中，使用tf函数搭建均衡系统并绘制单位阶跃响应曲线。使用仿真软件系统提供的交互工具数据游标获取系统性能指标。在暂态过程，描述控制系统时域响应的性能指标通常有最大超调量、峰值时间、上升时间[7]。最大超调量指系统输出超过输入终值的最大偏移量，上升时间指系统响应从终值的0.1至0.9需要的时间[8]。从单位阶跃响应图中可知，系统的最大超调量为0，上升时间为2.1 s，峰值时间为7.64 s。在稳态过程，稳态误差的终值为0。

采用最小二乘法获取均衡系统输入信号。使用c2d函数对均衡系统传递函数进行离散化，得到系统离散模型。当系统传递函数最高只有一阶信号时，通常选择单位斜坡函数作为系统输入信号，根据输入输出数据构建系数矩阵，根据最小二乘法原理对系数矩阵进行辨识，得出系统输入的拟合值，将其代入离散系统，并使用d2c函数将辨识后的离散系统转化为传递函数为：

作最小二乘法辨识后系统的单位阶跃响应图可知，经最小二乘法辨识后的系统的最大超调量为0，上升时间为2.1 s，峰值时间为6.87 s。稳态误差的终值为0。有效提高了均衡系统输入信号的可靠性，缩短了均衡时间，降低了不一致性问题带来的影响，具有更好的均衡效果。

3.2.2 电容放电过程的时域分析

由式（6）可知，电容在放电过程系统的传递函数为：

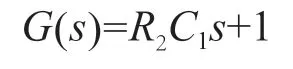
在仿真软件系统中，使用tf函数搭建均衡系统并绘制单位阶跃响应曲线。从单位阶跃响应曲线可知，系统的最大超调量为0，系统响应从终值的0.1至0.9需要的时间约为2.1 s，峰值时间为6.34 s。

采用最小二乘法获取均衡系统输入信号。使用c2d函数对均衡系统进行离散化。选择斜坡函数作为系统输入信号。根据系统输入输出数据构建系数矩阵，并根据最小二乘法原理对系数矩阵进行辨识，得出系统输入的拟合值，将其代入离散系统，并使用d2c函数将离散系统转化为传递函数为：

作最小二乘法辨识后系统单位阶跃响应曲线可知，经最小二乘法辨识后的系统的最大超调量为0，系统响应从终值的0.1至0.9需要的时间约为2.1 s，峰值时间为5.86 s。与算法辨识前的系统相比，提高了系统输入信号的可靠性和均衡时间，有效降低了电池组中各单体电池存在的不一致性问题，提高了电池组整体性能，延长了电池组使用寿命，符合最小二乘法的实际辨识效果。

4 设计

4.1 均衡系统模型搭建

课题组采用仿真软件系统根据设计的电路结构搭建均衡系统模型并进行仿真验证，均衡系统模型由系统启停控制模块、控制模块、电池组模块、均衡电路模块四部分组成。

4.2 均衡系统仿真分析

系统仿真模型搭建完成后，进行仿真参数的设置及仿真结果的运行、分析。通过Powergui模块，可以对系统进行定步长离散系统仿真[9]。根据系统性质将仿真类型选择为Discrete（离散型），仿真算法选择ode45算法[10]，其余参数保持系统默认值。

单击模型窗口中的“RUN”选项，系统开始仿真。仿真结束后，通过示波器模块观察系统仿真结果。通过仿真结果可知，电池组B1、B2电压值逐渐趋于一致，实现电池组间能量转移。

5 小结

综上所述，锂离子电池作为车用电池时常将多个单体电池串联或并联成电池组使用，由于其生产制造和使用中的差异，在经过多次充放电后，电池组内各个单体电池的容量、功率、寿命等参数会发生变化，出现不一致性问题。该现象对动力电池的安全性能、续航里程、使用寿命都会产生严重影响，并且是不可逆的。针对电池组不一致性问题，对电池均衡技术展开研究，使用最小二乘法对电路模型的数学模型进行参数辨识，提高均衡系统输入信号可靠性，并在仿真软件系统中设计出一套均衡系统仿真模型，通过均衡系统降低电池在生产和使用过程中产生的不一致性问题带来的影响，从而提高动力电池组的使用容量与寿命。