DD5高温合金单晶叶片振动频率的试验研究*

孙洪元，马德新，龚晓毅，赵运兴，员莹莹，魏 冰

（1. 中南大学粉末冶金研究院，长沙 410083；2. 深圳市万泽中南研究院有限公司，深圳 518045）

经过几十年的发展，航空发动机工作时涡轮前进气口温度越来越高，推重比进一步增大，这对涡轮叶片的合金材料及其制造工艺提出了更高的要求。相比于高温合金等轴晶和定向晶叶片，单晶高温合金叶片具有更出色的蠕变持久性能和热机械疲劳性能[1–3]，如等轴晶合金K417 在850℃/500 MPa 下的持久时间为30 h[4]，二代单晶合金DD6 在同样条件下持久时间约为500 h[4]，DD6 持久性能是K417 的17 倍。因单晶高温合金具有更优异的力学性能[5]，越来越多的单晶叶片被应用到航空发动机与燃气轮机高低压涡轮工作叶片和导向叶片中[6–8]。其中镍基单晶高温合金为面心立方结构，材料物理特性具有各向异性，即弹性模量、泊松比等参数均具有方向性，结晶取向的偏离将直接影响叶片的疲劳强度和振动等性能[1，9]。

目前，关于结晶取向对高温合金单晶叶片振动频率影响的研究较少。陶仙德等[10]研究了结晶取向对DD3单晶叶片固有频率的影响，采用有限元法分析了该叶片的前6 阶静频和45000 r/min 工作转速下该叶片的前6 阶振动频率在相应结晶取向范围内的变化规律，发现第二欧拉角对该叶片的低阶固有频率影响较大，但该研究未涉及实测数据。张根等[11]研究了晶轴偏转 （结晶取向偏离）对DD6合金带冠叶片频率特性的影响，采用有限元分析方法，对 DD6 单晶带冠叶片进行静应力和模态分析，获得了不同偏转角下叶片固有频率及叶冠间挤压力的变化规律，但未将固有频率与结晶取向之间的关系进行量化分析。张江伟等[12]以某型号航空发动机高压涡轮转子叶片为研究对象，对其叶冠进行改型分析，发现叶冠改型后叶片各阶固有频率均略有降低。王瀚艺[13]对某故障涡轮叶片进行延展改型并通过ANSYS 有限元进行验证，发现改型后的叶片成功避开了原叶片发生故障时的频率。

鉴于目前有关叶片结晶取向和叶片结构对振动频率影响方面的研究并不充分，本文对两种结构的DD5 合金低压涡轮转子叶片振动频率进行测量研究，对影响因素进行探讨，可为叶片结构的设计与振动频率控制提供基础数据。

1 试验方法

本研究采用的合金材料为第二代单晶高温合金DD5，合金成分见表1。

表1 DD5 合金的化学成分（质量分数）Table 1 Chemical composition of DD5 alloy (mass fraction) %

本研究制备的产品为某型航空发动机带冠低压涡轮转子叶片，改型前为A 型结构，改型后为B 型结构（图1），两者的高度、叶冠结构和榫齿至缘板的结构完全相同，设计重量也相同。不同的是A 型叶片的叶身带有排气窗口，而B 型叶片没有。另外，A 型叶片实际重心位置比B 型叶片的更靠近榫齿，B 型叶片的扭角在A型叶片基础上进行了调整。

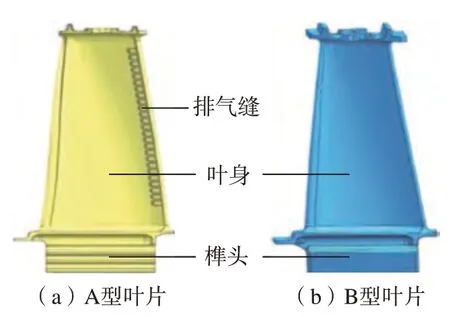
图1 两种结构叶片的外形示意图Fig.1 Schematic image of two structural blades

用常规的熔模法制备叶片浇注用陶瓷型壳，所有单晶叶片均采用德国ALD 公司的真空定向凝固炉（VIM–IC/DS/SC）铸造而成。单晶叶片均按以下不同工艺进行标准热处理：固溶热处理为1300 ℃，保温2 h +氩气冷却； 1 次时效处理为1120 ℃，保温4 h +氩气冷却； 2 次时效处理为1080 ℃，保温4 h +氩气冷却； 3 次时效处理为900 ℃，保温4 h +氩气冷却。对叶片采用完整的机械加工、喷丸、涂层等成品叶片加工工序。

采用加拿大Proto 公司的劳厄晶体衍射仪 （LAUE COS XRD）对两种单晶叶片的一次与二次晶向偏离角（分别记为β和α）进行检测，如图2 所示[11]。根据技术标准要求，一次晶向偏离角（β< 15°）的单晶叶片作为晶向合格产品，对二次晶向偏离角α未作要求。

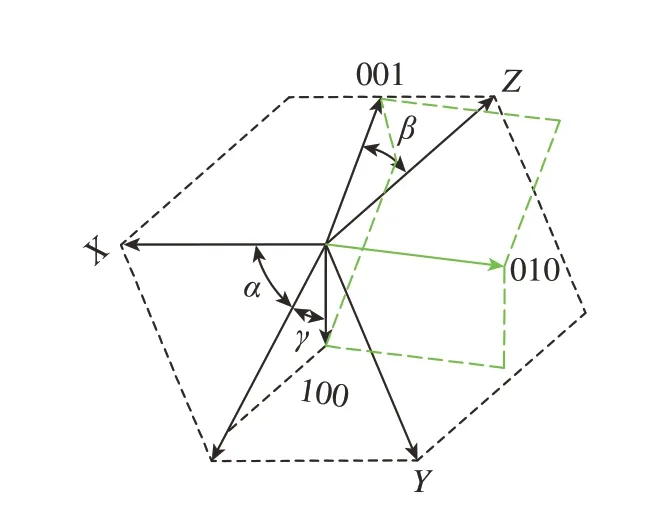
图2 一次与二次结晶取向偏离角示意图[11]Fig.2 Schematic image of primary and secondary crystal orientation deviation angles[11]

如图3 所示[11]，分别将A 型与B 型叶片的榫头采用专用夹具刚性夹紧 （夹紧力固定），然后固定到定制的专用振动台上，采用敲击共振法对叶片一阶弯曲振动频率 （简称振动频率）进行检测。

图3 叶片测频装夹[11]Fig.3 Clamping of vibration frequency measurement for blades[11]

2 结果与讨论

2.1 A 型叶片振动频率

对68 件β< 15°的A 型叶片，按照β值从小到大的顺序测量振动频率，结果如表2 所示。该型叶片振动频率的要求值为（395±20） Hz，测量结果显示有18 件叶片超出规格上限值415 Hz。该型叶片外形尺寸和壁厚尺寸等均满足设计要求，但出现了高达26.5%的频率超标的报废叶片，需要分析原因并进行改进。

从表2 可以看出，超标的频率主要分布在β值较大的区域。在β< 7.5°的前43 件叶片中，仅有 3 件的频率超标，超标率为7.0%；而在7.5°<β< 15°范围的后25 件叶片中，却有15 件频率超标，超标率高达60%。可见当β值增大时，不仅叶片机械性能逐渐变差，频率超标率更是显著增大，严重影响单晶叶片的成品率。因此需要加强对单晶铸件定向凝固工艺的控制，尽可能减小一次晶向偏差。

2.2 B 型叶片振动频率

B 型叶片为A 型叶片的设计改进版，去掉了尾缘排气窗口，并调整了叶型尺寸。对44 件β< 15°的B 型单晶叶片进行振动频率测量，结果如表3所示。该型叶片振动频率要求值与A型叶片一样，为 （395±20） Hz。从表3可以看出，仅有β值最大的44 号叶片的频率较高，超出规格上限415 Hz。

通过对比表2 和表3 发现， B 型叶片中的频率超标率仅为2.3%，比A型叶片的26.5%的平均频率超标率低了约1 个数量级。实际上B 型叶片的频率平均值约为405.9 Hz，低于A 型叶片的频率平均值（约413 Hz），更接近标准要求值 （395±20） Hz。这说明B 型叶片在结构上有利于降低频率，能够实现较高的频率合格率。

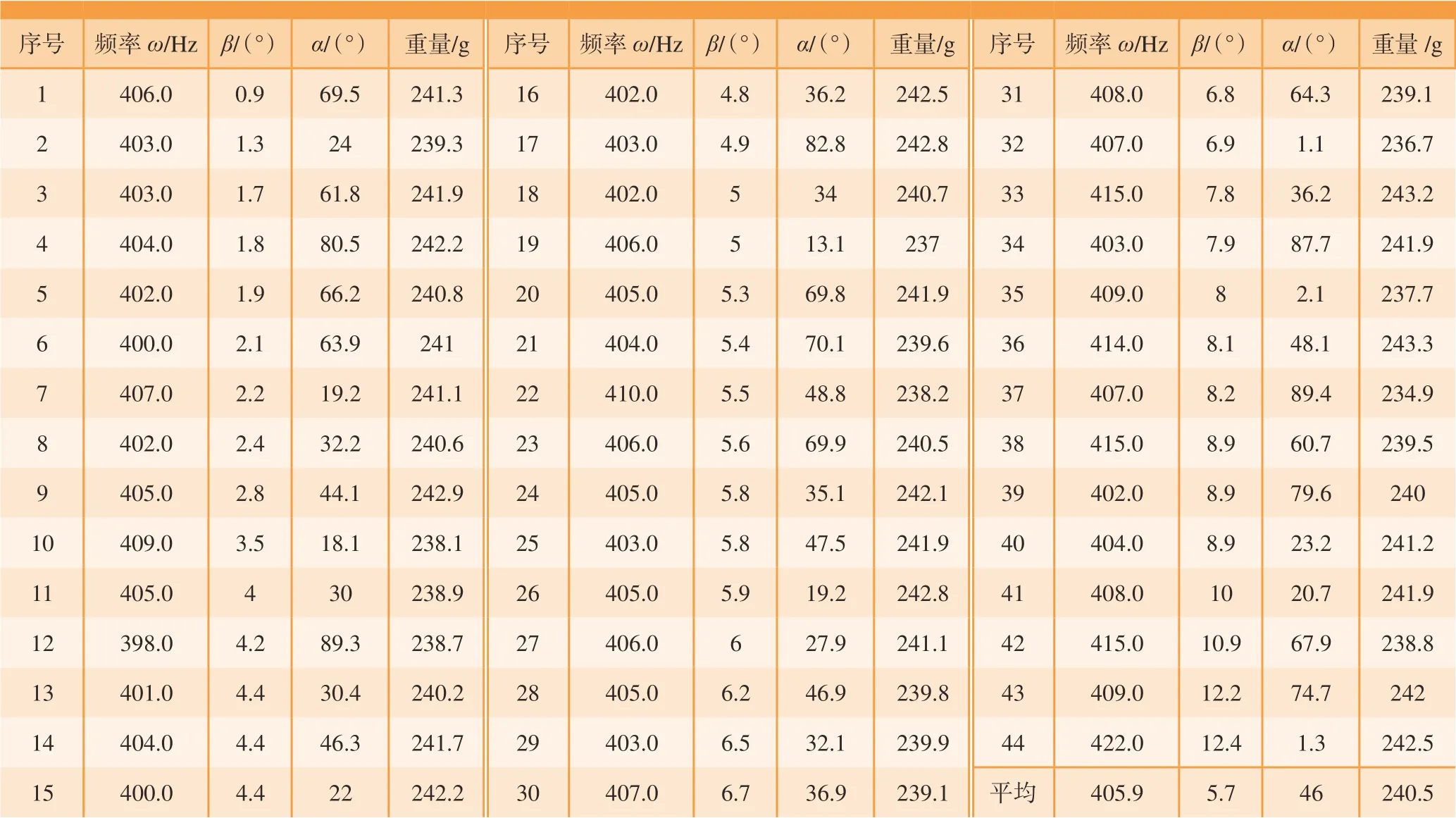
表3 B 型叶片振动频率测量结果Table 3 Vibration frequency of blade type B

2.3 影响叶片振动频率的相关因素

叶片无阻尼自由振动方程为[14]

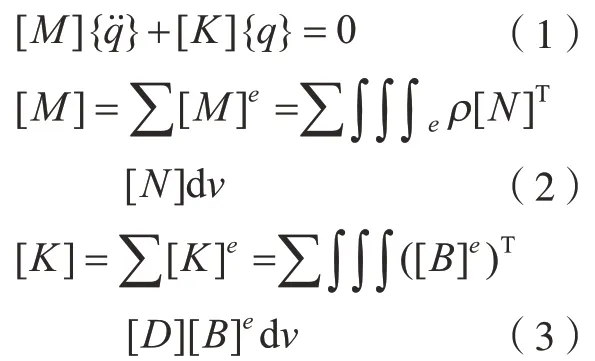
式中，[M]为总质量矩阵；[K]为总刚度矩阵；{q}为节点位移矩阵；[N]为形状函数矩阵；[B]e为应变–位移矩阵，[D]为弹性矩阵。

设解的形式为

式中，{Φ}为振幅列向量，是时间t的函数；ω为频率。将式（4）代入式（1）得

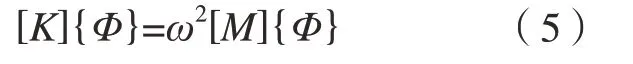
求解式（5），即可得到叶片的各阶固有频率。

从式（5）可以看出，频率ω主要与叶片的总刚度矩阵[K]和总质量矩阵[M]相关。

表2 中A 型叶片频率平均值约为413 Hz，接近规格上限，超标率高，可能是由于刚度矩阵偏大或者重量矩阵偏小。

表2 A 型叶片振动频率测量结果Table 2 Vibration frequency of blade type A

对于叶片的刚度，一方面叶片结构会对其产生影响；另一方面，在叶片结构一定时，影响刚度的主要为弹性模量 （结晶取向、内部组织等影响弹性模量），经金相检测分析比较叶片内部组织无明显差异，所以推测结晶取向为影响频率的重要因素，包括一次晶向偏离角β和二次晶向偏离角α。

对于重量矩阵，有两个方面的影响因素，即重量大小和重量分布。

2.4 振动频率的相关性分析

采用QI Macros 软件对A 型和B 型两种结构叶片的频率与一次晶向偏离角β、二次晶向偏离角α、重量的相关性进行分析，分析结果如表4所示。

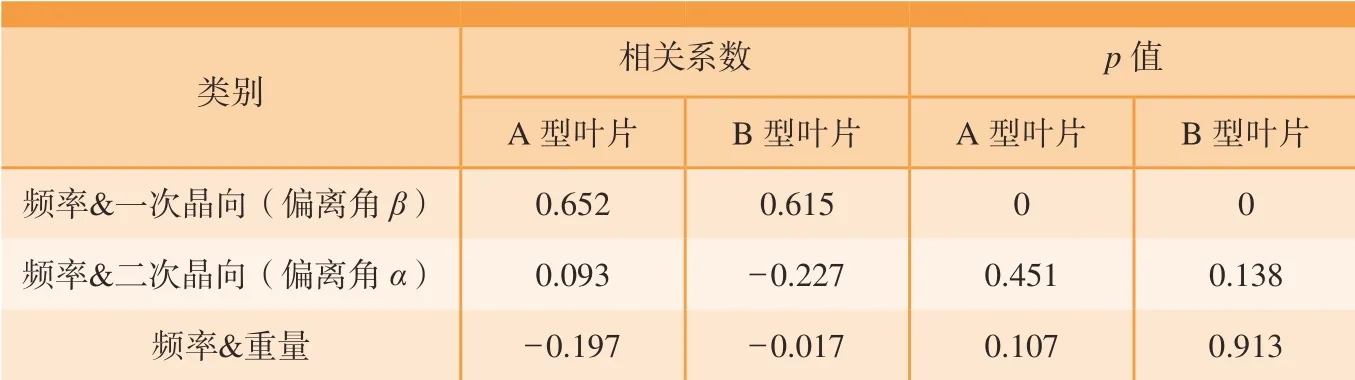
表4 A 型和B 型叶片振动频率与一次晶向偏离角β、二次晶向偏离角α 和重量的相关性Table 4 Vibration frequency of blade type A&B correlated with primary orientation β,secondary orientation α and weight

可以看出，A 型和B 型叶片频率与一次晶向偏离角β的相关性系数分别为0.652 和0.615，p值均为0，具有显著相关性，并且呈正相关；A 型和B 型叶片频率与二次晶向偏离角α的相关性系数分别为0.093和– 0.227，p值均大于0.05，基本不具有相关性。A 型和B 型叶片频率与重量的相关性系数分别为– 0.197 和– 0.017，p值均大于0.05，基本不具有相关性。

2.5 一次晶向偏离角β 与振动频率的关系

分别将A 型叶片 （68 个）与B型叶片 （44 个）的振动频率测量数据，以一次晶向偏离角β为横坐标，振动频率ω为纵坐标，绘制成散点图，如图4 所示。

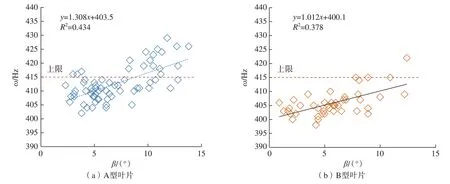
图4 A 型与B 型叶片振动频率ω 与一次晶向偏离角β 的关系Fig.4 Relationship between vibration frequency ω and primary orientation deviation angle β of blade type A and B

拟合得到的线性方程见式 （6）和 （7），拟合后关系式的决定系数R2分别为0.434 和0.378，发现频率与β呈线性正相关，与表4 得出的结论一致。

按式（6）和（7）计算，在一次取向为10°时，A 型与B 型叶片的振动频率分别为416.6 Hz 和410.2 Hz。可以看出，通过降低叶片的一次晶向偏离角β可以解决单晶叶片振动频率超出设计上限的问题。按表2 和表3 数据，如果将一次结晶取向偏离角的控制范围由β< 15°改进为β< 10°，A 型叶片频率超标率将由26.5%降到13.5%，而B 型叶片则全部合格。

由式（6）计算得到，A 型叶片在一次晶向偏离角β由0 增加到15°时，振动频率由404.9 Hz 提高到423.1 Hz，增加了4.5%；由式（7）计算得到，B 型叶片在一次晶向偏离角β由0 增加到15°时，振动频率由400.1 Hz 提高到415.2 Hz，增加了3.8%。

张根等[11]采用ANSYS 有限元法对DD6 合金的某型带冠叶片也进行了类似分析，结果为一次晶向偏离角β=15°时的频率比β=0 时的大5%，与本文研究结果接近，说明振动频率随一次晶向偏离角的增加而不断提高，如图5 所示。

图5 某DD6 叶片振动频率ω 与一次晶向β 的关系[11]Fig.5 Relationship between vibration frequency ω and primary orientation deviation angle β of a DD6 blade[11]

图6[15]为Wells 模型和Voigt 模型得到的杨氏模量与一次晶向的关系图，可以看出，一次结晶取向在0～15°变化时，杨氏模量均呈现接近线性增加。由于叶片的刚度同样随着杨氏模量的增加而增加，所以推测振动频率随着一次晶向的增大而增大，本质上是由杨氏模量的变化引起的。

图6 杨氏模量与一次晶向的关系[15]Fig.6 Relationship between Young’s modulus and primary orientation deviation angle[15]

2.6 二次晶向偏离角α 对振动频率的影响

分别将A 型叶片 （68 个）与B型叶片 （44 个）的振动频率测量数据，以二次晶向偏离角α为横坐标，振动频率为纵坐标，绘制成散点图（图7），发现数据较发散。将A 和B型叶片频率测量数据与二次取向偏离角α进行拟合，拟合后关系式的决定系数R2分别为0.0099 和0.0517，发现无明显相关性，说明二次取向不是影响振动频率的主要因素。

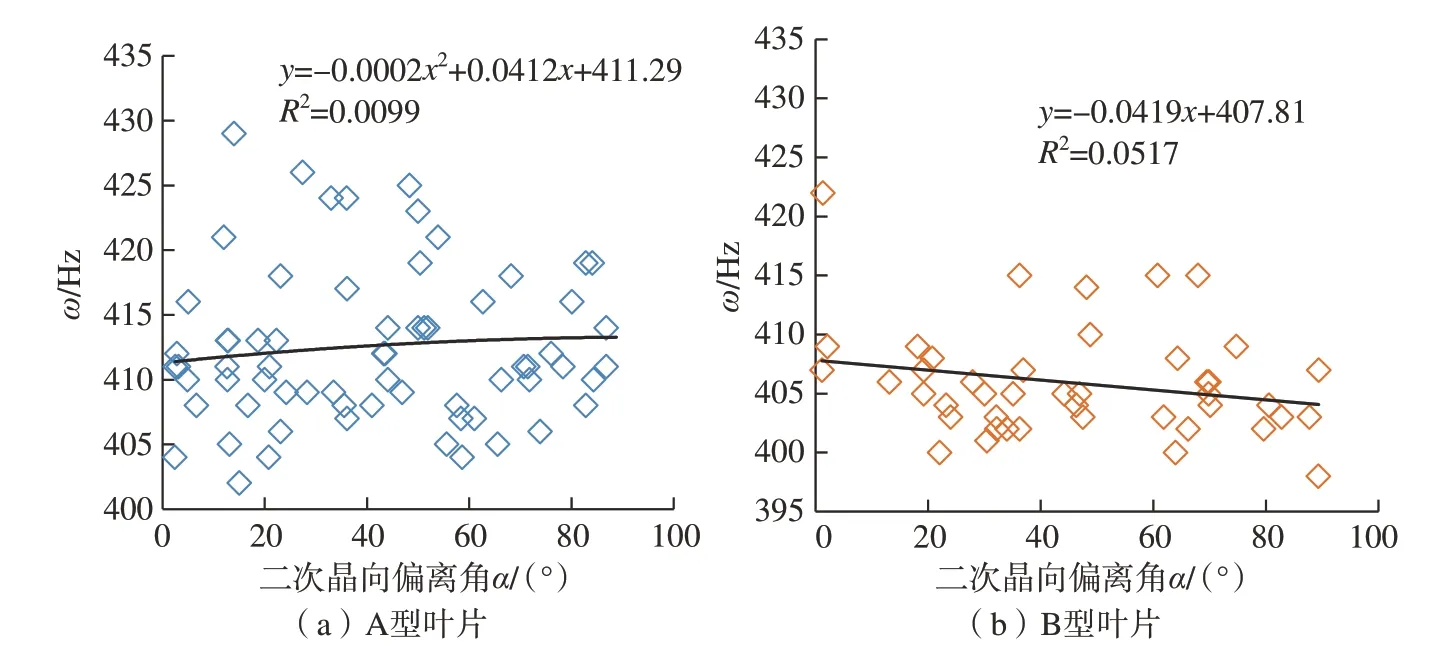
图7 A 型与B 型单晶叶片振动频率与二次晶向的关系Fig.7 Relationship between vibration frequency ω and secondary orientation deviation angle α of blade type A and B

2.7 重量大小与重量分布的影响

分别以A 型叶片 （68 个）与B型叶片 （44 个）的涂层重量为横坐标，振动频率为纵坐标，绘制成图8，拟合得到关系式的决定系数R2分别为0.0428 和0.0003。根据式（5）得出叶片的振动频率与重量有着密切关系，但从图8 来看，随重量增大A型叶片振动频率仅有小幅度下降，而B 型叶片振动频率无明显变化。A 型和B 型叶片的重量控制较严格，波动范围分别为242～249.5 g 和234.9～243.3 g ，约3%的重量变化未引起振动频率的明显变化。特别是叶片的重量主要集中在厚大的榫头部位，但进行振动试验时榫头被专用夹具夹紧，被敲击振动的主要是空心薄壁的叶身部位。由于各个叶片在叶身部位的重量差别较小，所以不会引起叶身振动频率的明显变化，也就无法证明叶片重量大小与振动频率的相关性。

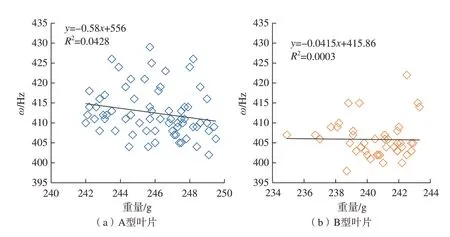
图8 A 型与B 型叶片振动频率与重量的关系Fig.8 Relationship between vibration frequency ω and blade weight of type A and B

为了排除一次取向偏离角β的干扰，将表2 和3 中β< 10°的叶片测量数据进行统计，得出A 型与B型叶片平均重量分别为246.1 g 和240.5 g，而两者的平均振动频率分别为410 Hz 和405.2 Hz，也就是说，重量较大的A 型叶片的振动频率也较大，但似乎与常识不符。根据上面所述，叶片的重量主要集中在不参与振动的厚大榫头部位，所以叶片的振动频率并不取决于叶片的总重量，而是与参与振动的叶身本身的结构和重量等因素有关。A 型叶片叶身的尾缘开有一列排气缝，比起具有封闭尾缘的B 型叶身减轻了重量，也使得叶身的重心更靠向被夹紧固定的榫头，这些因素都使得A 型叶身的振动频率增大。

3 结论

（1）单晶叶片的一次晶向偏离角β对振动频率值ω有显著影响，ω值随β值的增大而显著增大。但二次晶向偏离角α对叶片振动频率的影响较小。

（2）叶片的振动频率与叶身的结构密切相关，但叶片总重量对其影响不显著，这是因为重量集中的厚大榫头部位并不参与振动。

（3）为了有效控制叶片铸件的振动频率，在设计上应该优化叶身结构，在铸造过程中尽量减少一次晶向的偏离。