航空发动机叶片阵列抛光轨迹调整技术研究*

张 云，陈志同，朱正清

（1.北方工业大学，北京 100144；2.北京航空航天大学，北京 100191）

叶片是航空发动机中数量最多、且直接参与能量转换的核心动力部件[1]，其加工质量及生产效率尤为重要。目前，国内航发制造企业仍大规模采用人工打磨方式进行叶片抛光，但随着叶片设计、材料、工艺体系的快速发展，对于已经完成型面精加工的批量叶片，高效率、自动化数控抛光成为替代人工打磨、保证抛光质量的有效手段之一[2]。

数控抛光的工艺灵活性和装备适应性较强[3]，主要实现形式为以砂带、砂布轮、橡胶轮等为工具的工业机器人和数控机床抛光[4]。近年来，为了全面替代人工打磨，在保证抛光质量的前提下，众多学者开展了大量抛光提效研究。其中，华中科技大学徐小虎[5]通过力–位双控及工艺参数优化，使得机器人砂带磨抛效率相较于人工打磨可提高50%以上。重庆大学Xiao[6]和Li[7]等研制出多工位集成自适应砂带磨抛系统，具备上料、检测、力控调整等自动化功能。西北工业大学淮文博[8]和Chen[9]等根据弹性工具抛光原理建立了抛光效率的数学模型，并结合正交试验结果的灰色关联度优化抛光参数组合。北京航空航天大学陈志同等[10]为提高抛光效率研制了可同步加工多个叶片的多主轴阵列加工系统。德国亚琛工业大学与STAMA 公司的研究表明，当采用双主轴阵列机床时，平均单件加工成本和工时可降低到单主轴机床上加工同样两件工件的70%以下[11–12]。然而，由于叶片制造面临薄壁结构、复杂曲面、难加工材料等难点，型面精加工后叶片普遍存在线轮廓度、位置度、相对扭转等误差[13]。为此，本团队依据误差分布情况开展批量叶片数字化分组研究，以降低阵列抛光时各叶片间的型面差异[14]。但同组叶片实际型面与理论模型间仍存在差异，由理论模型生成的抛光轨迹极易出现过抛、漏抛等问题。因此，本文以叶片变形分析及进排气边抛光工艺试验为基础，开展阵列抛光轨迹自动化调整研究，在保证抛光精度及表面质量的前提下，达到高效率、自动化多主轴阵列抛光的目的。

1 多主轴同步定轨迹抛光

1.1 多主轴同步抛光

如图1 所示，多主轴 （2×2）同步加工机床具有3 个移动轴X、Y、Z和2 个转动轴B、C，主轴摆头B转动角度为±45°，回转工作台C为360°连续转动，多支 （2×2）轮式抛光工具通过标准刀柄连接至B上，工件通过快换工装安装于C上，通过工具与叶片间的轨迹控制，即定轨迹轮式抛光方式，实现高效率的同步抛光。

1.2 定轨迹轮式抛光

定轨迹轮式抛光采用具有准确尺寸和确定弹性的柔性工具（图2（a）），该工具设计直径为D，环面管半径为ρ。当给定转速ω时，该工具在预压量E下与叶片表面接触后被压缩产生弹性变形，进而提供稳定可控的接触压力，使得工具表面附着的超硬磨料对接触表面起到抛光作用（图2（b））。

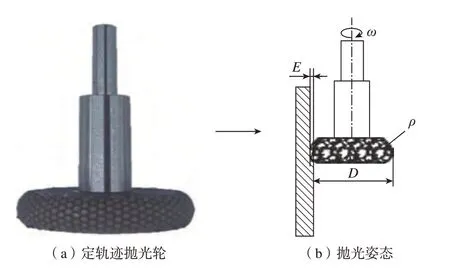
图2 定轨迹轮式抛光Fig.2 Wheel polishing with determined-path

2 叶片变形分析及抛光工艺试验

精加工后叶片实际型面普遍存在设计公差内容许的线轮廓度、位置度、相对扭转等误差，而这些误差又显著影响进排气边区域的实际形状，图3（a）给出了第4 节验证实例中9 件抽样叶片进排气边区域的测量结果。当抽样叶片采用阵列抛光时，各叶片实际形状差异，尤其在进排气区域，将导致抛光预压量E的差异，进而造成阵列抛光后各叶片抛光去除量ε和表面粗糙度Ra存在差异。因此，阵列抛光轨迹应在考虑上述差异的影响下实现自动调整。

针对验证实例中型面精加工后待抛光叶片进排气边圆弧半径r范围 （r= 0.1～0.3 mm），设计如图3（b）所示圆弧试件r= 0.1 mm、0.2 mm、0.3 mm，开展抛光工艺试验建立预压量E与抛光去除量ε、表面粗糙度Ra的关系，如式（1）和（2）所示。

式中，拟合参数a1/a2= –0.34/–0.37，b1/b2= 0.57/–7.81，c1/c2= 0.98/1.44，d1/d2= –0.1/23.71，g1/g2= –1.5/–0.55，h1/h2= 0.012/0.82。图4 给出了E与ε、Ra关系图，如r= 0.1 mm 时，随着E（E= 0.05 mm、0.10 mm、0.15 mm、0.20 mm）的增加，ε增加，而Ra先降低后增加。而实际上，图3（a）所示型面精加工后叶片实际形状存在差异，造成阵列抛光时实际预压量较理论值存在差异。所以，应结合叶片实际形状对阵列抛光轨迹中实际预压量进行调整，保证叶片各不同圆弧半径处抛光去除量的差异最小，同时抛光表面质量满足设计要求。

图3 叶片变形分析及抛光工艺试验Fig.3 Blade deformation analysis and polishing process

图4 对r = 0.1 mm、0.2 mm、0.3 mm 试件抛光建立E 与ε、Ra 关系曲线Fig.4 Relationship of E and ε, Ra for r = 0.1 mm, 0.2 mm, 0.3 mm workpieces

3 阵列抛光轨迹调整

阵列抛光轨迹调整主要包括3个步骤。

（1）测量规划。采用接触式扫描测头对叶片进行测量，但由于对象为批量叶片，应尽可能减少测量时间。由第2 节分析可得各叶片进排气边处差异显著，因此测量点应分布于进排气边处，为实际预压量调整提供测量数据。

（2）最优配准。将各测点处实际预压量和曲率半径共同代入式（1）和 （2），可得到执行当前抛光轨迹后各测点处表面粗糙度和抛光去除量。而在轨迹调整时，以抛光后表面粗糙度为约束，以实际预压量引起的抛光去除量差异最小为配准目标函数，通过求解旋转和平移量实现最优配准。

（3）轨迹调整。由数控系统坐标转换功能对阵列抛光轨迹所在加工坐标系进行旋转与平移，实现实际预压量的在机调整，从而提高阵列抛光加工的效率和自动化程度。

3.1 阵列抛光叶片的测量规划

采用同一加工轨迹进行阵列抛光的叶片数量记为n，在理论加工坐标系MCS下由定义截面蒙皮方式构建的叶片型面记为S（u，v）。采用三坐标测量机 （配置接触式扫描测头PH10M SP25M）检测如图5 所示测量曲线 （红色线条，是进排气边与盆背转接点的等u线，u= 0、0.45、0.50、0.95），由测量曲线与定义截面求交可获得m个测量点，则n件叶片的测量点集为P= {pij|i= 1，…，n；j= 1，…，m}。

3.2 面向阵列抛光的最优配准

通过最小二乘拟合算法求解S（u，v）与P之间的平移与旋转变换矩阵RT，考虑到计算复杂度和截面定义方式，如图5 中RT的参量简化为绕着Z坐标轴的旋转分量Δγ和沿着X、Y坐标轴的平移分量Δx、Δy。pij至S（u，v）的最短距离点为qij=S（uij，vij），相应点集记为Q={qij|i= 1，…，n；j= 1，…，m}。

图5 叶片扫描测量线示意图Fig.5 Sketch of blade measurement

则在目标函数minF（RT）下以=Q·RT逐步逼近P，其中=qij·RT，当相邻迭代目标函数差值小于指定阈值时，迭代终止。

在MCS下，由S（u，v） 生成的阵列抛光加工轨迹为GPath，由工艺要求确定各点理论预压量函数为E0（u，v），则在qij处实际预压量为vij）。其中，（uij，vij） 为S（u，v） 在处的外法矢方向。给定在处的曲面曲率半径为r（uij，vij），则依据式（1）和（2）计算抛光去除量εij和抛光后表面粗糙度Ra，ij为

给定目标函数minF（RT）为阵列抛光时各叶片测量点处抛光去除量差异最小，则可写作

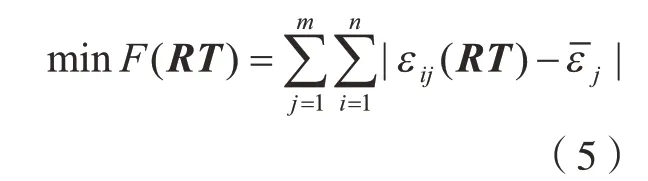
式中，为（i= 1，…，n）处的去除量均值。当要求叶片抛光表面粗糙度达到Ra0.4 μm 以下时，给定约束条件为

由式（5）和 （6）求解RT为典型的非线性约束优化问题，可用非线性优化算法进行求解 （Δx，Δy，Δγ），本文不再详述[15]。

3.3 阵列抛光轨迹的在机调整

由3.2 节所得 （Δx，Δy，Δγ）对GPath 进行调整。如图6 所示，由于在数控系统中加工轨迹执行先旋转再平移的绝对变换，因此由MCS形成新的加工坐标系MCS'时，式（7）给出了先旋转Δγ后的平移量Δx'、Δy'计算方法。

图6 阵列抛光轨迹调整–坐标变换Fig.6 Array polishing path adjustment–coordinate transformation

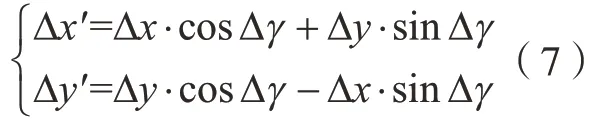
则调整后的阵列抛光轨迹GPa'th采用Simense 840D 数控系统坐标转换功能对GPath 进行自动调整，代码释义如表1 所示。

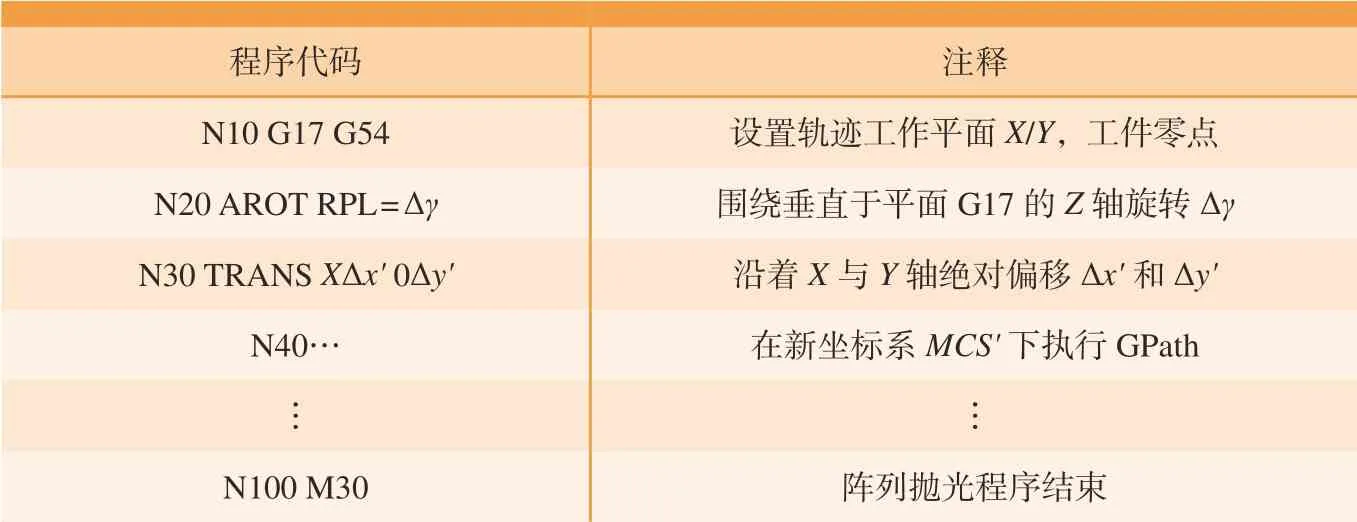
表1 GPa'th 的G 代码与注释Table 1 G-code and its denote of GPa'th

4 阵列抛光加工验证

所验证实例为某型号航空发动机压气机叶片，材料为高温合金，如图7所示，尺寸规格约为22 mm×35 mm，依据型面几何属性确定柔性轮式工具尺寸为D= 29.6 mm、ρ= 1.5 mm。

图7 阵列抛光加工验证叶片模型Fig.7 Array polishing blade model

对待阵列抛光验证的4 件叶片进行三坐标测量，测量曲线与定义截面求交可获得如图8 所示的测量点集P。

图8 4 件待阵列抛光叶片的测量结果Fig.8 Measurement result of 4 blades before array polishing

将P代入式（5）和（6），利用外罚函数法求解得到Δx= –0.024 mm，Δy= +0.0103 mm，Δγ= –0.262°。则对4 件待抛光叶片进行坐标变换，重新计算P至S（u，v）的偏差值，结果如表2 所示。

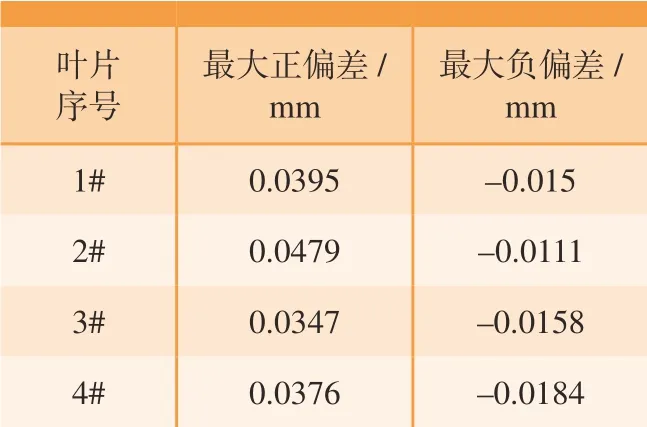
表2 4 件叶片坐标变换后的偏差分析Table 2 Deviation analysis of 4 blades after coordinate transformation

用式（7）换算后Δx'= –0.0241 mm，Δy'= 0.0102 mm，图9 举例给出了在MCS'下叶背、进气边加工程序。阵列抛光过程如图10 所示，包括粗抛光、半精抛光和精抛光过程，所用抛光轮的磨料及主要抛光工艺参数如表3 所示。

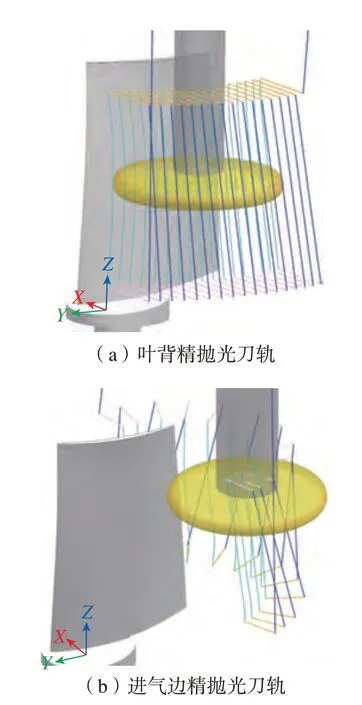
图9 叶背、进气边精抛光加工程序Fig.9 Finishing polishing machining program for pressure side and leading edge

图10 4 件叶片阵列抛光加工工况Fig.10 Array polishing for 4 blades

目前，在航空发动机制造企业中该叶片采用人工打磨方式，单件打磨时间约为10 min。而采用表3 中抛光轮和工艺参数进行单件抛光时，粗抛、半精抛、精抛工时分别约为4.5 min、3 min 和3.5 min，则单件抛光工时约为11 min，此时单件抛光效率较人工打磨略有降低。而采用4 主轴阵列抛光后，由于同步抛光4 件叶片，平均单件抛光工时约为11/4 min = 2.75 min，阵列抛光效率比人工打磨提高了约2.6 倍。因此，采用阵列抛光后效率提升明显。

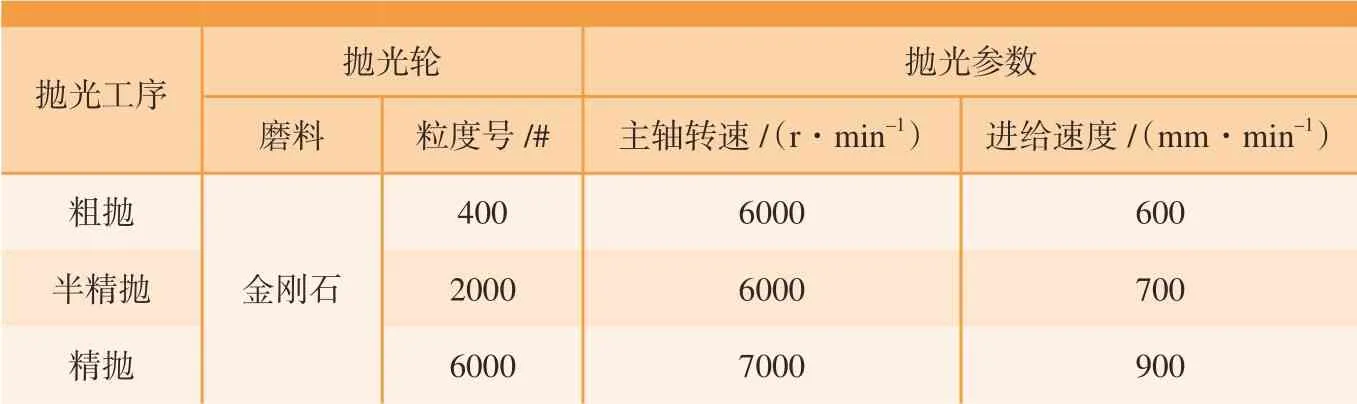
表3 阵列抛光所用抛光轮磨料和工艺参数Table 3 Polishing wheel abrasive and polishing parameters

采用三坐标测量机对抛光后4 件叶片进行精度检测，盆/背的最大/最小误差 （CV/CC_MAX/MIN）、进/排气边的最大/最小误差 （LE/TE_MAX/MIN）如表4 所示。则1# ～ 4#叶片经过阵列抛光后，由最大误差与最小误差的差值确定的线轮廓度分别为0.031 mm、0.032 mm、0.0265 mm 和0.0306 mm。

表4 4 件叶片表面粗糙度和精度分析Table 4 Surface roughness and accuracy analysis of 4 blades

采用车间型精密粗糙度轮廓仪（Form TalySurf Intra）对抛光后4 件叶片的中间截面进行表面粗糙度检测，表面粗糙度Ra< 0.4 μm，满足设计要求。

5 结论

本文针对阵列抛光加工轨迹的自动调整需求开展技术研究，并利用典型型号叶片进行了阵列抛光验证，取得的主要结论如下。

（1）结合叶片关键区域抛光预压量与抛光去除量、表面粗糙度的工艺试验分析结果，对阵列加工轨迹的配准变换进行了有效求解，并利用数控系统坐标转换功能完成G 代码的自动调整，实现阵列抛光过程轨迹调整的自动化。

（2）4 件典型叶片经过阵列抛光后，线轮廓度分别达到0.031 mm、0.032 mm、0.0265 mm 和0.0306 mm以内，表面粗糙度Ra< 0.4 μm，阵列抛光质量得到保证。同时，平均单件叶片抛光工时达到2.75 min，抛光效率提升明显。