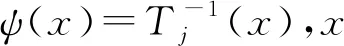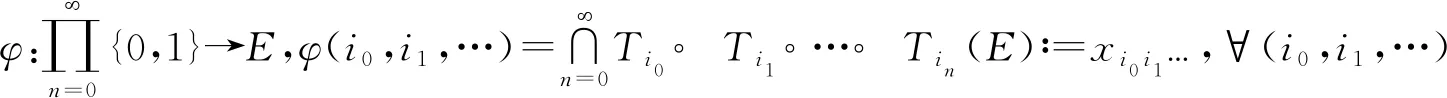关于IFS的一个经典遍历定理的注记
杨荣领, 马东魁
(1. 广州城市理工学院计算机工程学院, 广州 510800; 2. 华南理工大学数学学院, 广州 510640)
在拓扑动力系统中,拓扑熵[1]是一个拓扑共轭不变量,可用来刻画系统的复杂程度。非紧集的拓扑熵[2-3]与测度熵、Lyapunov 指数等密切相关[4-11],可用来研究系统中的重分形谱[12]、饱和集[6]和非正则集等[5,7]。
学者们从多个角度对拓扑熵进行了深入研究,发现系统中满足一定条件的零测集具有与整个系统相同的拓扑熵或Hausdorff 维数。如:BARREIRA和SCHMELING[4]证明了针对拓扑混合的有限型子转移,如果Hölder 连续函数g对0是非上同调的,那么g的Birkhoff 平均不规则集上的拓扑熵等于这个有限型子转移的拓扑熵;PESIN[5]证明了针对符号系统,非generic 点集上的拓扑熵等于整个系统的拓扑熵;CHEN等[6]证明了满足specification性质的非正则集上的拓扑熵等于整个系统的拓扑熵;TIAN[7]证明了系统中若干周期类点集的差集上的拓扑熵等于整个系统的拓扑熵;ZHU和MA[8]将文献[6-7]的结论推广到了自由半群作用的系统中。
在迭代函数系统(IFS)中,ELTON[13]得到了一个遍历定理(Elton定理):对任意连续函数,符号空间中几乎所有的点,IFS 的时间平均等于空间平均。受文献[4-8]的启发,本文探讨符号空间中Elton定理不成立的点构成的集合的性质及其拓扑熵、Hausdorff 维数与整个系统的拓扑熵、Hausdorff 维数的关系。
1 主要结果
设(X,d)是紧致度量空间。映射T:X→X称为一个压缩映射,如果d(T(x),T(y))≤θd(x,y),∀x,yX,其中θ(0<θ<1)是一个常数。如果{T0,T1,…,Tm-1}是X上的压缩映射族,那么称(X,T0,T1,…,Tm-1)为迭代函数系统(IFS)。由文献[14]可知,对于迭代函数系统(X,T0,T1,…,Tm-1),如果存在唯一的非空子集E⊂X,使得则E被称为(X,T0,T1,…,Tm-1)的吸引子。
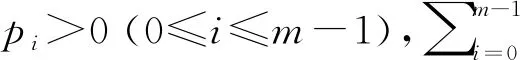
且suppν是(X,T0,T1,…,Tm-1)的吸引子E,这个概率测度ν称为是(X,T0,T1,…,Tm-1)的关于概率向量(p0,p1,…,pm-1)的不变测度。

1987年,ELTON[13]得到了迭代函数系统(X,T0,T1,…,Tm-1)中的一个遍历定理:
定理A[13](Elton定理)对于X上的任意连续函数f和任意xX,有
相对于乘积测度P而言,对几乎所有的(j0,j1,…)Σ成立。
对任意fC(X)和任意xX,记f的Elton定理不成立的点构成的集合为
B1(f,x)={(j0,j1,…)
Tj0(x))不存在}。
根据定理A,对Σ上的每一个乘积测度P,均有P(B1(f,x))=0,B1(f,x)是σ-不变的,其中σ是Σ上的推移映射。
本文研究集合B1(f,x)的拓扑熵、Hausdorff维数与整个系统的拓扑熵、Hausdorff 维数的关系。
设A为m×m阶矩阵,A的每个元素aij取值为0或1。设ΣA⊂Σ是紧致的σ-不变子集,使得任意(i0,i1,…)ΣA,满足ainin+1=1,n≥0,映射σ|ΣA称为由矩阵A决定的有限型子转移。称σ|ΣA拓扑混合当且仅当存在一个正整数k,使得Ak的所有元素的值都是正的。σ|ΣA的拓扑熵为h(σ|ΣA)=logρ(A)[15],其中ρ(A)表示A的谱半径。
如果存在连续函数ψ:ΣA→,存在c,使得g1-g2=ψ-ψσ+c,则称2个函数g1,g2:ΣA→是上同调的。对于每一个连续函数g:ΣA→,定义g的Birkhoff平均的不规则集为
B(g)={(j0,j1,…)不
存在}。
注意,集合B(g)是σ-不变的。根据Birkhoff 遍历定理[15],对于ΣA上每一个σ-不变测度μ,有μ(B(g))=0。1997年,BARREIRA和SCHMELING[4]证明了满足一定条件的Birkhoff 平均不规则集上的拓扑熵等于这个有限型子转移的拓扑熵。
定理B[4]对于拓扑混合的有限型子转移,如果 Hölder 连续函数g对0是非上同调的,那么
h(σ|B(g))=h(σ|ΣA),
其中,h(σ|B(g))、h(σ|ΣA)分别表示B(g)、ΣA上的σ拓扑熵,B(g)表示g的Birkhoff平均不规则集,ΣA表示由矩阵A确定的符号空间Σ的σ-不变子集。
下面给出本文定理证明需要用到的一个结论:
定理C[12]对符号系统(Σ,σ),对任意Z⊂Σ,有
h(σ|Z)=HD(Z)·logm,
其中,Σ由m个符号生成,h(σ|Z)表示Z上的拓扑熵,HD(Z)表示Z上的Hausdorff维数。
本文主要结论如下:
定理1设(X,T0,T1,…,Tm-1)是一个迭代函数系统,对任意gC1(X)和任意xX,这里C1(X)={gM(X),ν1≠ν2},M(X)表示(X,T0,T1,…,Tm-1)中关于所有概率向量的不变测度的集合,有
h(σ|B1(g,x))=h(σ)=logm,
即B1(g,x)是满熵的,且具有满Hausdorff维数。
证明仿照定理B的证明方法,设(p0,p1,…,pm-1)和(q0,q1,…,qm-1)是任何概率向量,且
(p0,p1,…,pm-1)≠(q0,q1,…,qm-1)。
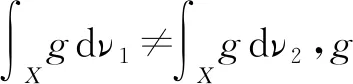


μ(C)=P1(C),CD1=C1,

对于每个可测集A⊂Σ,令μ(A)=μ(A∩Λ),则μ扩展到了Σ上。

如果ε<2,那么
设(j0,j1,…)CDs,由于(j|C|-ms,j|C|-ms+1,…)当s→∞时,有因此,如果s足够大,那么
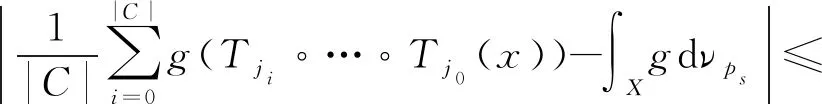


由于δ(0,ε),可知Λ⊂B1(g,x)。现在设(j0,j1,…)Λ,如果q足够大,那么
对某η(0,2ε)成立。这意味着
h(σ|B1(g,x))≥h(σ|Λ)≥hμ|Λ(σ)≥h(σ)-2ε,
由于ε是任意的,则h(σ|B1(g,x))=h(σ)。
此外,由定理C可得
证毕。
2 例子
例1设X=[0,1],T0:x的吸引子是Cantor集E:
(i0,i1,…)
取gC(X),使得g(x)=a,x[0,1/3],g(x)=b,x[2/3,1],这里a≠b。对于任意xX,令E(g,x)={xi0 i1…|(i0,i1,…)B1(g,x)}⊂E。那么以下结论成立:
(1)对于任意的xX,有
h(σ|B1(g,x))=h(σ)=log 2,HD(B1(g,x))=HD(Σ),
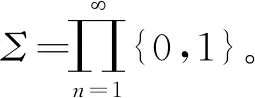
(2)对于任意xX,有
HD(E(g,x))=HD(E)=log 2/log 3。
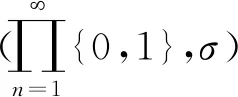
定理D[11]对紧致系统(X,f),若存在α>1,对任意充分小的正数ε,当d(x,y)<ε时,有d(f(x),f(y))=αd(x,y),则对任意Z⊂X,有
h(f|Z)=HD(Z)·logα。
例1的证明(1)设(p0,p1)和(q0,q1)为任意概率向量,且(p0,p1)≠(q0,q1)。那么p0≠q0,p1≠q1。设ν1、ν2分别表示(X,T0,T1)关于(p0,p1)、(q0,q1)的不变测度,则ν1≠ν2,且
因此
(p0a+p1b)-(q0a+q1b)=a(p0-q0)+b(p1-q1)=
(p0-q0)(a-b)≠0,
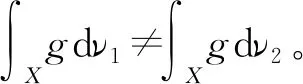
h(σ|B1(g,x))=h(σ)=log2,HD(B1(g,x))=HD(Σ)。
(2)对于迭代函数系统(X,T0,T1),可以定义一个连续的自映射
ψ:E→E,