基于原型网络的小样本脑电伪迹检测方法
李景聪, 林镇远, 潘伟健, 吴潮煌, 潘家辉
(华南师范大学软件学院, 广州 510631)
脑电信号(Electroencephalogram,EEG)是由大脑活动引起的一种生理电信号。由于其无创、安全和低成本的特点,脑电信号技术已经在医疗和娱乐等领域得到了广泛的应用,比如应用于非侵入式的脑机接口系统[1-2]、癫痫疾病的检测[3]和睡眠分期[4]。在脑电采集过程中影响正常脑电信号的不良脑电信号被定义为脑电伪迹[5],通常是由生理现象(比如眨眼、咀嚼、肌肉运动等)或外部来源(比如电极干扰)产生的。在脑电信号分析过程中,脑电伪迹往往会造成不利的影响。换句话说,为了使基于脑电信号技术的应用保持足够的性能,提高脑电信号的信号质量是关键,而提高脑电信号的质量关键是更好地检测并处理脑电伪迹。
最早期的脑电伪迹检测方法是使用伪迹避免和人工检测的方法[6]。其中,使用伪迹避免的方法是通过指示受试者尽量避免进行无关动作来消除伪迹,易导致诱发电位振幅的变化以及给受试者带来额外的认知负荷[7];人工检测的方法需要脑电图专家人为地识别、检测脑电图中存在的伪迹,但该方法带主观性且耗时。因此,目前更多的研究集中在脑电伪迹的自动检测方面,旨在提供一种客观、自动的伪迹检测方法。如:提出了一种基于信号处理和统计学的伪迹检测方法,并成功地将该检测方法在临床上用于相关疾病的唤醒试验(Wake fulness Test,MWT)[8];提出了一种基于小波变换的自适应滤波方法,以自动去除脑电记录中的眼电伪迹[9];提出了一种有效阈值小波变换与自适应滤波相结合的方法,根据眼电伪迹在低频域的分布情况提取参考信号,并采用基于最小均方(Least Mean Square,LMS)算法的自适应滤波方法去除脑电信号中的眼电伪迹[10];利用希伯特变换的方法自动地去除几种典型的脑电伪迹[11];提出基于独立成分分析(Indepen-dent Component Analysis,ICA)的自动伪迹检测方法,该方法从混合信号中计算独立分量:首先利用矩阵算法计算各信号分量,再通过信号重建排除与伪迹相关的信号成分,从而最大程度地保留原始脑电信号[12-14]。但是,使用ICA很难检测和消除瞬态伪迹,如头颈部肌肉收缩产生的肌肉伪迹。此外,ICA需要很高的计算能力,而且,仅使用ICA的伪迹检测算法需耗费巨大的时间成本和人工成本。近年来,随着机器学习和深度学习技术的发展,机器学习和深度学习的方法也被应用在脑电伪迹检测和去除的研究中,并且显示出很大的潜力。如:提出了一种基于机器学习的自动伪迹检测算法,使用支持向量机结合人工神经网络的机器学习方法对ICA提取的特征进行分类,实现了端到端的、自动化的伪迹识别方式,在测试的脑电伪迹数据集上得到了95%的准确率[15];使用了一种贝叶斯网络结合注意力的深度学习方法来实现脑电伪迹的检测,改进了传统神经网络方法在训练过程可能无法准确预测具有未知分布的数据的问题,并取得了95.86%的检测准确率[16];提出一种基于卷积神经网络的多通道脑电信号伪迹检测方法,在7种不同类型的伪迹分类实验中得到的平均准确率为74%,且方法的分类准确率以及所耗费的计算资源均优于基于ICA的伪迹检测方法[17];为了检测多通道脑电信号中的各种伪迹,提出了一种低复杂度的基于长短时记忆神经网络(Long Short-term Memory,LSTM)的伪迹检测模型,该模型在二分类实验中的伪迹检测准确率达到93.1%,优于使用卷积神经网络和自回归模型的伪迹检测方法[18]。
虽然深度学习方法有较好的识别能力,但是需要依赖于大量的数据集且需要较长的训练时间。而小样本学习方法旨在使用较少的样本数量来训练神经网络,同时能够得到接近基于大量样本的训练模型的性能[19],因此,学者们着眼于小样本学习方法的研究。如:提出一种用于单样本任务图像识别的孪生神经网络模型,在Omniglot数据集上的识别能力与人工识别图像的能力相当[20];提出一种用于单样本任务图像识别的匹配神经网络模型,在Ominiglot、ImageNet数据集上分别取得了98.1%、98.9%的准确率[21];设计了一种用于解决小样本分类问题的原型网络,该网络学习一个度量空间,在这个度量空间内每个类用其原型表示,而不是单个的点,然后通过计算与该类原型的距离来实现小样本分类[22]。
为了解决脑电伪迹数据集不足的问题,本文提出一种仅使用少量脑电伪迹进行训练的脑电伪迹原型网络模型,旨在使用小样本学习方法,仅使用目标类别少量的数据来实现脑电伪迹检测并保持稳定的性能。受最新的小样本学习方法原型网络[22]的启发,设计了一个基于原型网络的脑电伪迹识别模型(EEG Artifact Prototype Network,EAPNet)。该模型由特征嵌入、距离模块和分类模块组成,仅需使用少量的训练数据进行训练就能得到高效的检测性能。最后,在公开脑电伪迹数据集TUAR上,在2-wayK-shot(K=1,5,10)任务中分别进行了EAPNet模型与7个机器学习模型和2个深度学习模型的对比实验、4种度量方法的EAPNet模型的对比实验以及探究样本量对EAPNet模型影响的实验。
1 脑电原型网络方法
1.1 EAPNet总体框架
小样本学习问题[23]可描述为:首先给定一个数据集,其中数据可以表示为X={x1,x2,…,xn},其对应的标签集合可以表示为Y={y1,y2,…,yn},(xi,yi)C表示第i个数据和对应的标签,C表示所有类别数据和对应标签的集合;然后,在数据集中切分可见类数据集Cseen和不可见类数据集Cunseen;最后,使用可见类数据训练模型,以便模型能够很好地泛化不可见类数据。本文的目标是首先使用来自Cseen的数据训练模型,将训练后得到的模型使用Cunseen上少量的数据实现模型的快速适应,进而实现对Cunseen的分类。小样本学习模型的每次迭代是以任务作为对象的,小样本学习任务被称为N-wayK-shot任务[20],该任务构建时从集合Cseen和Cunseen中分别采样N个类,并且从每个类中采集K+Q个带标签的样本构成任务T。这K个带标签的样本称为支持集用于评估模型性能的数据集称为查询集其中任务T中每个类都包含Q个测试样本。在训练时,从Cseen中采集样本以构造多个任务训练模型;在测试时,从Cunseen中采集样本构造多个任务来最终评估模型的识别性能。
图1展示的是一个解决2-wayK-shot小样本任务的EAPNet模型框架,该框架包含1个编码器F、1个距离模块Dist和1个分类模块Soft。图中表示的2类伪迹分别是颤栗伪迹和电极伪迹,即Cunseen为颤栗伪迹和电极伪迹的数据集合。需要强调的是这里展示的是使用模型进行实际分类时的场景,使用Cseen(眼电伪迹和咀嚼伪迹的数据集合)训练时的场景与图1所示的框架是相同的,仅比图1多了1个反向传播的步骤,故在此省略。另外,该框架还可以扩展到N-wayK-shot学习任务。

图1 EAPNet模型框架图
在Cseen上进行EAPNet模型的训练过程可描述如下:首先,在Cseen上进行训练,即编码器F从眼电伪迹和咀嚼伪迹中提取特征,将其嵌入高维空间;然后,分类模块使用Softmax激活函数,将距离模块计算的距离负值形成概率分布;最后,使用交叉熵损失函数根据概率分布和标签计算损失,通过反向传播调整编码器参数。在Cunseen上实际进行脑电伪迹(颤栗伪迹和电极伪迹)的预测过程可描述如下:首先,分别计算通过编码器的颤栗伪迹和电极伪迹的信号特征原型;然后,通过距离模块计算信号特征原型和查询信号特征的距离;最后,分类模块使用Softmax激活函数,将距离模块计算的距离负值形成概率分布,根据概率分布输出查询信号的预测标签。
1.2 编码器
编码器F是EAPNet的子网络结构,每次以成对的K个支持样本和1个查询样本作为输入,该编码器结构参考了深度学习基线模型(EEGNet)[24],可以有效地提取脑电信号时间和通道间的特征信息。因此,EAPNet模型的编码器包含2个卷积块和1个非线性块:第1个卷积块由2个时域滤波器组成,第2个卷积块包含1个空域滤波器,非线性块包含1个全连接神经网络。为了方便输入CNN网络,把数据增加了1个维度,即处理成1×250×22的数据矩阵,矩阵每一维分别表示维度、时间和通道。在第1个卷积块中,第1个时域滤波器使用64个大小为25×1的卷积核,捕获10 Hz及以上的频率信息,然后以4×1的步长通过卷积核大小为4×1的最大池化层;使用16个大小为5×1的卷积核,对第2个时域滤波器的特征图进行筛选,然后以4×1的步长通过卷积核大小为4×1的最大池化层。在第2个卷积块中,模型的空域滤波器使用10个大小为1×22的卷积核提取脑电数据22个通道的信息。每次卷积操作后,分别使用批归一化和指数单元(ELU)进行非线性化。为了防止过拟合,本文使用了随机失活神经元技术(Dropout),并将失活概率设置为0.25。最后,把经过时域滤波和空域滤波后输出的特征融合,通过1个包含128个神经元的全连接层映射到非线性高维空间,从而把经过编码器输出的样本x的高维特征表示为F(x)。图2展示了EAPNet模型的编码器。

图2 EAPNet模型的编码器图
1.3 距离模块
距离模块采用余弦距离作为度量方法,而不是传统原型网络[22]中使用的欧氏距离。主要原因为:(1)欧氏距离是计算空间中样本间各点的绝对距离,与各个点的坐标相关;而余弦距离使用2个向量的夹角余弦值来衡量2个样本间的差异,更注重2个向量方向上的差异。(2)图像中每个坐标点的取值范围为0~255,均为正数,更适合使用欧氏距离作为度量方法;脑电数据由于电极的特性,每个电极采样的数据点是电压的幅值,所以脑电数据的数据点具有正负值,更适合使用强调方向差异的余弦距离作为度量方法。距离模块Dist主要是负责计算经过编码器输出后的不同样本在高维空间的余弦距离。其计算公式如下:
(1)
其中,F(x1)、F(x2)分别为经过编码器编码的样本x1、x2的高维向量。
1.4 分类模块
分类模块Soft主要负责将编码器和距离模块的输出通过Sotfmax激活函数形成概率分布,并根据最后的概率分布实现分类。
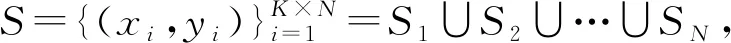
(2)
假设现在有1个查询样本zq,其高维空间特征向量可表示为F(zq)。利用模型的距离模块来计算查询样本高维向量F(zq)与原型CN的余弦距离,计算公式如下:
(3)
得到查询样本和CN的余弦距离后,通过Softmax函数,将查询样本zq和原型CN的余弦距离的负值在类上形成概率分布。计算公式如下:
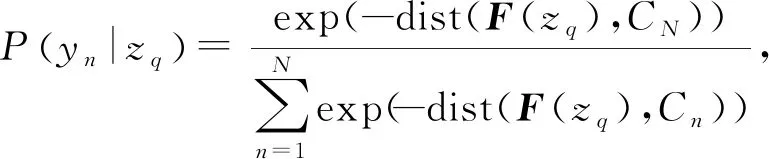
(4)
其中,Cn(n=1,2,…,N)为第n类的原型。
为了训练时模型有良好的评价指标,本文使用交叉熵作为损失函数Loss进行训练,然后最小化损失函数。计算公式如下。
(5)
其中,n为查询样本数量,yi为第i个样本的实际标签。
2 实验结果与分析
2.1 实验设计
2.1.1 数据预处理 TUAR数据集是天普大学提供的脑电伪迹数据库,是目前公开的最大的伪迹数据集,包含213个病人的5种常见的脑电伪迹,分别是眼动、咀嚼、颤抖、电极干扰、肌肉伪迹;所有数据采用250 Hz和400 Hz的采样频率进行采样,包含21个电极,电极位置按国际10-20系统的位置排列。该数据集旨在用于帮助提高脑电事件分类算法的性能,如癫痫检测算法。
首先,为了更好地消除信号噪声,并改善脑电图信号的空间信息解释,神经科学家常使用TCP(Temporal Central Parasagittal)双极导联组合的方式查看脑电图[25]。 因此,本文同样使用TCP双极导联组合的方式处理信号数据,从而得到22个通道的脑电数据重参考的通道电极位置(图3)。
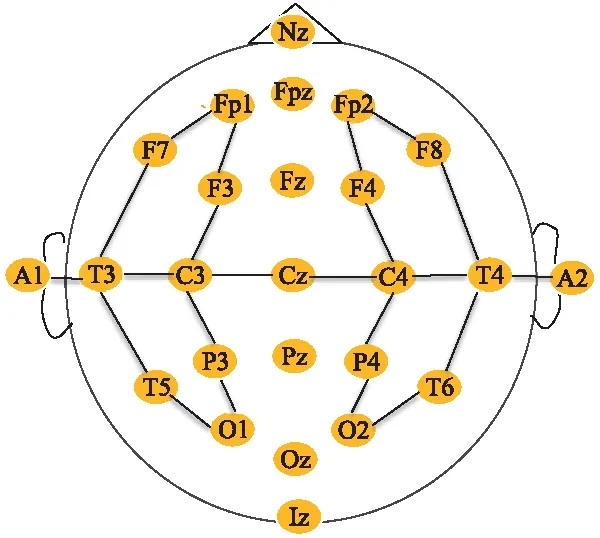
图3 带有22通道的TCP montage标准10-20系统的电极位置[26]
然后,将所有的脑电数据统一降采样为250 Hz,即把1秒内采集到的脑电信号作为1个样本。另外,为了滤除数据中无关的噪声,本文使用1个5阶的巴特沃斯滤波器(Butterworth filter)保留全部通道中0~250 Hz的脑电信号。
最后,为了保留空间信息且符合网络输入,把一维的通道位置重建为二维通道[27]。因此,EAPNet模型最后的输入为1×250×22的矩阵。 另外,随机选取了每类样本的170个样本,选取4类脑电伪迹(眼动、咀嚼、颤栗、电极干扰)作为本文的实验数据。其中,将眼动和咀嚼2类伪迹数据作为可见类数据,将颤栗和电极干扰2类伪迹数据作为不可见类数据。
2.1.2 实验设置 实验使用7折交叉验证。EAPNet模型在训练期间使用眼动和咀嚼2类伪迹数据作为Cseen进行训练。在每次迭代中,将Cseen中的样本分成2组集合:每类50个样本作为可选的支持集,剩余的120个样本作为查询集。同样地,测试时使用颤栗和电极干扰2类伪迹数据作为Cunseen,将Cunseen中的样本分成支持集和查询集,分布情况和训练时保持一致。
为了更好地评估EAPNet模型的性能,观察模型在2-wayK-shot(K=1,5,10)任务中的分类准确率。当K=1,5,10时,从50个支持集样本中随机选取K个作为支持样本。本文在相同设置下,将EAPNet模型与2个深度学习模型(EEGNet、全连接神经网络(Fully Connect Neural Network,FNN))、7个机器学习模型(高斯贝叶斯模型(Gaussian Naive Bayes,Gaussian NB)、随机森林模型(Random Forest,RF)、逻辑回归模型(Logistic Regression,LR)、 套索回归模型(Lasso Regression,Lasso)、支持向量机模型(Support Vector Machines,SVM)、岭回归模型(Ridge Regression,Ridge)和最近邻算法模型(K-Nearest Neighbor,KNN))进行性能对比。
由于实验结果可能会因为选取的支持集样本不同而出现差异,本文的实验重复进行了30次支持集的随机采样,将平均准确率和标准差作为最终的实验统计结果。
训练EAPNet模型时采用Adam优化器加速训练过程。实验表明:学习率设置为10e-6时,模型的训练效果最好。
2.2 对比实验结果
不同模型的对比实验结果(图4)表明: 在2-wayK-shot(K=1,5,10)任务中,EAPNet模型的性能最优。具体表现在:
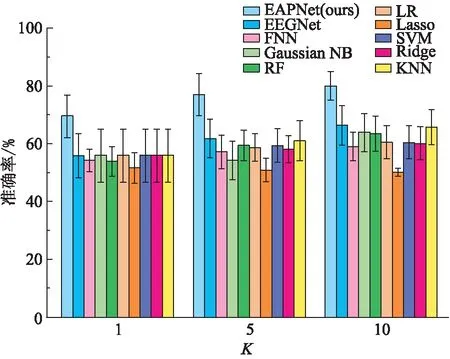
图4 10个模型的准确率对比
(1)在K=1,5,10时,EAPNet模型的准确率分别是69.44%、77.21%、80.01%, 均高于对比的7个机器学习模型和1个深度学习模型(EEGNet模型)。
(2)在K=5,10时,EAPNet模型的性能提升幅度最高,且保持较好的稳定性。
(3)EAPNet模型得益于神经网络强大的数据表征能力,对伪迹信号所提取的特征泛化能力强于7个机器学习模型。与EEGNet模型相比,有以下2个方面的优点:
①防止过拟合。EEGNet模型使用的基于原型网络的方法是一种基于度量的小样本学习方法,不仅有神经网络强大的数据表征能力,还很好地解决了因为数据太少导致的过拟合问题。具体地讲,神经网络分类器会存在一个高维的嵌入空间。即在原型网络中假设存在这样一个嵌入空间,在这个嵌入空间中每个类别数据的点会围绕一个原型。为了实现这一点,需要使用神经网络学习输入到嵌入空间的非线性映射,并将其在嵌入空间中的支持集的平均值作为类的原型,可以把原型认为是每个类的具有代表性特征的表示。但是,传统的深度学习网络存在目标类别数据有限而造成的过拟合问题,从而无法利用目标数据学习到有效的嵌入空间。而原型网络可以充分地利用非目标类别的数据,从而学习到一个在目标类别数据中也表现良好的嵌入空间。因此,原型网络在嵌入空间对非目标数据进行学习后,将少量的目标数据输入嵌入空间,然后从嵌入空间中计算原型和度量来实现分类,而无需使用目标数据来学习这个嵌入空间,从而避免了传统深度学习在数据量不足时容易带来的过拟合问题。
②提取的特征更加具有迁移性。原型网络属于度量学习的一种小样本学习方法,可以用于判断数据间的异同。该网络的嵌入空间提取的信息是用于区别数据之间异同的高维特征,可以认为该嵌入空间的信息是可迁移的,即使在面对训练时没见过的类别数据时也能有良好的性能。而传统的深度学习网络一般只针对目标数据进行学习,其嵌入空间只对网络学习过的数据类别有效,无法迁移到其他数据类别。
2.3 更换度量方法对EAPNet模型的影响
本文分别采用欧氏距离(Euclidean)、余弦距离(Cosine)、切比雪夫距离(Chebyshev) 和曼哈顿距离(Manhattan)4种常见的度量方法进行对比实验,观察将EAPNet模型的度量方法更换成其他度量方法后的模型准确率。由实验结果(表1)可知在小样本情况下,余弦距离在本实验中确实是最适用的度量方法:当K=1,5时,使用余弦距离为度量方式的准确率最高;当K=10时,使用余弦距离为度量方式的准确率仅略低于使用欧氏距离的。

表1 不同度量方法的EAPNet模型的准确率
2.4 样本量对网络性能的影响
已有研究[21]表明在N-wayK-shot任务中,N和K的设置会影响准确率:当N越小或者K越大时,准确率越高。为了验证EAPNet模型是否符合这个规律,本文研究在2-wayK-shot(K=1,2,5,10,15,20)任务中的准确率和标准差。由结果(图5)可知:随着K值的增加,EAPNet模型的准确率不断提高,模型的性能更加稳定。究其原因为:在网络结构一定的情况下,每类数据选取的样本越多,样本所能涵盖的范围分布越广,其特征平均值(原型)对该类的表征越准确。

图5 在2-way K-shot(K=1,2,5,10,15,20)任务中EAPNet模型的准确率和标准差
3 结论
本文使用小样本学习方法来解决脑电伪迹检测问题,提出了一种基于原型网络的脑电伪迹识别模型(EAPNet)。该模型在目标类别样本有限的情况下,实现了对脑电伪迹的正确识别,其检测识别性能优于其他基线方法的。另外,受益于深度学习网络强大的数据表征能力,该模型仅对输入信号数据做了极少的预处理,而由深度学习网络自动地从原始信号中提取更深层的特征,从而实现了端到端的脑电伪迹识别。
本研究也表明,在脑电伪迹检测中,小样本学习方法是一种具有优越性能和发展前景的方法,其有望提高脑电伪迹的检测能力,从而得到更高质量的脑电信号,因此,基于小样本学习的伪迹检测方法有利于提高基于脑电图技术的脑机接口系统的性能。

